北师大版四年级下册数学第二单元知识点复习课件 (共45张PPT)
文档属性
| 名称 | 北师大版四年级下册数学第二单元知识点复习课件 (共45张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 18:34:03 | ||
图片预览








文档简介
(共45张PPT)
认识图形
图形的分类
三角形分类
三角形内角和
三角形边的关系
四边形分类
数图形中的学问
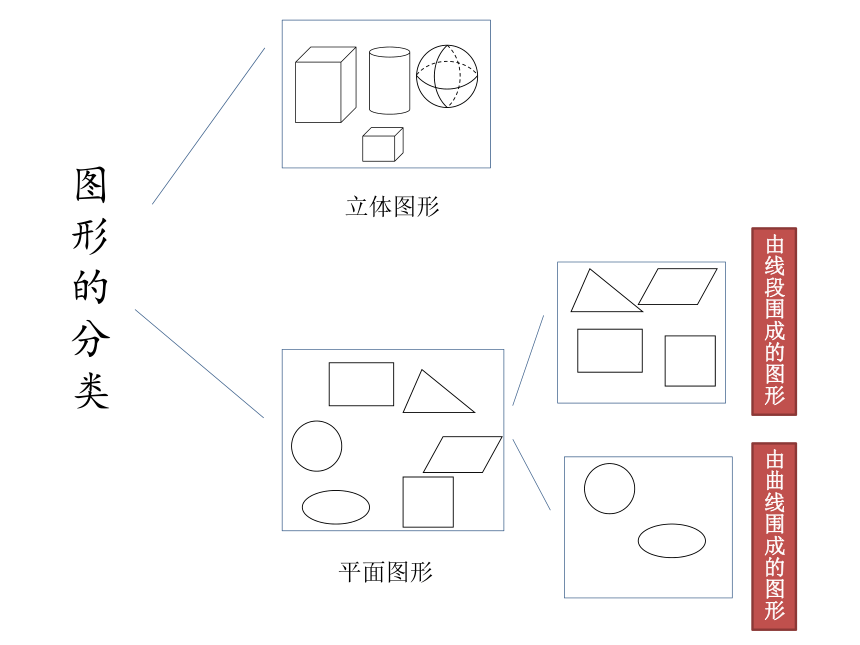
图形的分类
立体图形
平面图形
由线段围成的图形
由曲线围成的图形
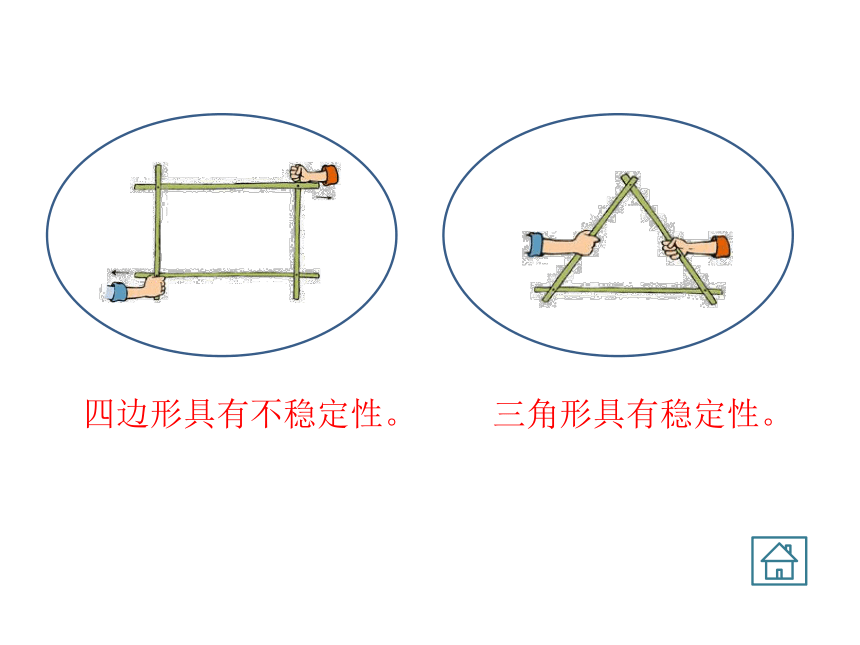
三角形具有稳定性。
四边形具有不稳定性。
练习题
1、平行四边形容易( ),三角形具有( )。
2、三角形是( )图形,球形是( )图形。
3、由四条线段组成的图形是四边形 。( )
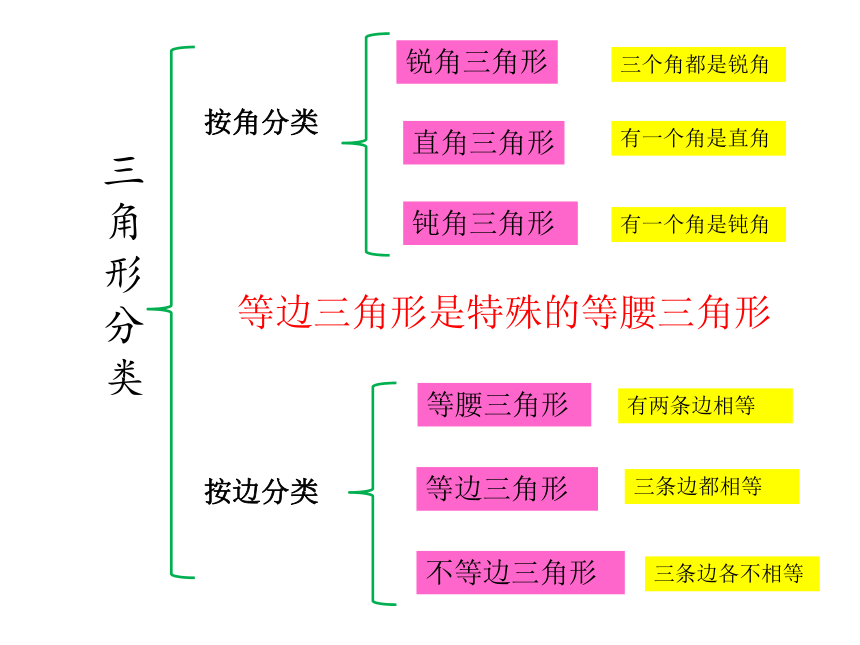
三角形分类
按角分类
按边分类
锐角三角形
直角三角形
钝角三角形
等腰三角形
等边三角形
不等边三角形
三个角都是锐角
有一个角是直角
有一个角是钝角
有两条边相等
三条边都相等
三条边各不相等
等边三角形是特殊的等腰三角形
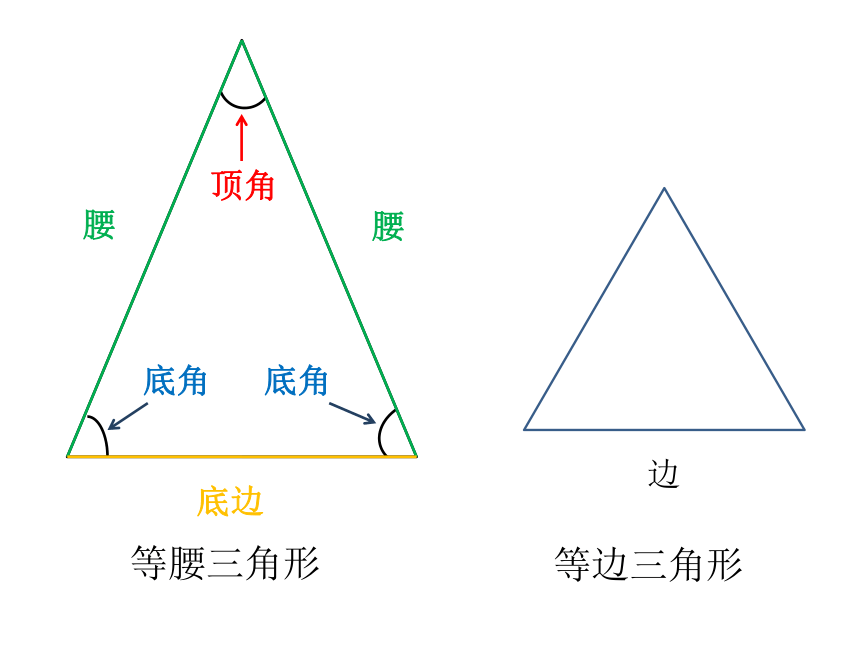
等腰三角形
顶角
底角
底角
腰
腰
底边
等边三角形
边
1.找一找,填一填。
图形 是等腰三角形,
图形 是等边三角形,
图形 是直角三角形,
图形 是钝角三角形,
图形 是锐角三角形。
④ ⑤ ⑧ ⑨
⑥ ⑦
③ ⑧
② ⑨
① ④ ⑤ ⑥ ⑦ ⑩
巩固练习
填空题
1、由一个角是( )角的三角形叫做直角三角形。
2、有一个角是钝角三角形叫做( )
3、由三条线段( )的图形叫做三角形。
4、三角形有三条( )和( )个角。
5、( )的三角形叫做锐角三角形。
6、一个三角形中至少有( )个锐角,最多有( )个锐角。
7、三角形按角分为( )三角形、( )三角形和( )三角形。
8、等边三角形又叫( )三角形,它的三条边都( )。
9、等腰三角形两腰间的夹角是( ),腰与底边的夹角是( )。
2、判断:(用手势表示)
(1)、有一个角是锐角的三角形是锐角三角形。
(3)、所有的等腰三角形都是锐角三角形。
(4)、等腰三角形是特殊的等边三角形。
×
×
( )
( )
(2)、所有的等边三角形都是锐角三角形。
( )
√
(5)、有一个角是直角的三角形就叫做直角三角形。
( )
√
( )
×
(6)一个三角形里有两个锐角,必定是锐角三角形。( )
(7)一个三角形里至少有两个锐角。( )
(8)等边三角形都是等腰三角形。( )
(9)在所有的钝角三角形中,不可能有等腰三角形。( )
×
√
√
×
选择题
1、锐角三角形有( )
A、两个锐角 B、一个锐角 C、三个锐角
2、三角形中的一个角是100°,这个三角形是( )三角形。
A、锐角 B、直角 C、钝角
3、一个最小的锐角是50°,这个三角形一定是( )
A、钝角 B、直角 C、锐角
4、一个三角形,其中两个角的平均度数是45°,这个三角形是( )三角形
A、锐角 B、直角 C、钝角
解决问题
1、小亮用3米长的铁丝做了一个等边三角形形状的风筝。风筝的边长是6分米,铁丝剩下多少米?
2、小强想用2米长的铁丝做一个等腰三角形形状的风筝。风筝的腰长是6分米,它的底边长是多少分米?
思考题:
图(1)中分别有( )个锐角三角形,( )个钝角三角形,( )个直角三角形。
?
?
图(2)中分别有( )锐角三角形,( )个钝角三角形,( )个直角三角形。
1
2
2
2
2
4
三角形内角和等于180°。
内角
外角
+
=180 °
内角
外角
1
2
外角= ∠1+∠2
三角形的内角和是180 °
四边形的内角和是360 °
180 °×2
五边形的内角和是540 °
180 °×3
六边形的内角和是720 °
180 °×4
选择题
1、三角形内角和是( )
A、180° B、360° C、90°
2、在直角三角形中,一个锐角是30°,另一个锐角是( )。
A、30° B、60° C、90°
3、一个等腰三角形的顶角是60 °,它的底角是( )
A、60° B、45° C、30°
4、把一个三角形从一个顶点用一条直线分成两个三角形,其中一个三角形的内角和是( )
A、90° B、180° C、360°
5、一个三角形有两个角是锐角,则第三个角是( )
A、一定是锐角
B、一定是钝角
C、一定是直角
D、可能是锐角或钝角或直角
判断题
1、三角形越大,内角和就越大。( )
2、等边三角形一定是锐角三角形。( )
3、一个底角是42°的等腰三角形一定是钝角三角形。( )
4、直角三角形的两个锐角和正好等于90°。( )
5、钝角三角形的内角和大于锐角三角形的内角和。( )
6、在钝角三角形中,两个锐角的和大于90°。( )
7、三角形中有一个角是60°,那么这个三角形一定是个锐角三角形。( )
8、一个三角形中一定不可能有两个钝角。( )
9、一个三角形中最多只能有一个直角。( )
10、用一个10倍的放大镜看一个三角形,这个三角形的内角和是1800°。( )
计算下面三角形中角的度数
1、在直角三角形中,一个角是45°,求另一个角。
2、在一个三角形中,一个角是30°,另一个角是60°,求第三个角。
3、在一个三角形中,∠1=130°,∠3=25°,∠2是多少度?
4、一个等腰三角形的顶角是20°,底角是多少度?
算一算,内角和是多少?
两边的差<第三边的长度<两边的和
判断题
1、三角形任意两条边长度的和一定比第三条边大。( )
2、一个三角形,它的三边长度可以分别是3厘米、6厘米、10厘米。( )
3、三角形最长的一条边有可能等于其他两边的和。( )
4、在一个三角形中,较大的角对应的边较长,较长的边对应的角也较大。( )
5、三角形中任意两边之差都小于第三边。( )
6、在三角形中,有两条边都为4厘米,那么第三条边一定大于4厘米。( )
7、用三根同样长的小棒不能围成三角形。( )
判断下面几组线段能围成三角形吗?为什么?
(1)3厘米、4厘米、5厘米
(2)2厘米、4厘米、6厘米
(3)3厘米、6厘米、4厘米、
(4)2厘米、4厘米、8厘米
如果一个三角形的两条边的长分别是4厘米、6厘米,那么第三条边的长应该在什么范围内?
四边形
梯形
平行四边形
长方形
平行四边形
梯形
两组对边分别平行且相等的四边形,叫做平行四边形。
只有一组对边平行的四边形,叫做梯形。
1、等腰三角形的一个顶角是48 °,它的一个底角是( )
2、( )形和( )形是特殊的平行四边形。
3、两个完全相同的直角三角形,可以拼成( )形。
4、如果将长方形的对角用力拉后,此长方形就变成了 ( )形。
5、一个三角形的两条边分别是9厘米和13厘米,第三条边必须比( )厘米大,比( )厘米小。
填空:
61°
长方
正方
正方形、长方形
平行四边
4
22
二、我是公正的小法官。(对的打“√”,错的打“×”)
1. 等边三角形也是等腰三角形。 ( )
2. 所有三角形的内角和都相等。 ( )
3. 等腰三角形不可能是钝角三角形 。 ( )
4. 把任意一个三角形放在放大镜下,就成了钝角三角形。 ( )
5.平行四边形也是特殊的梯形. ( )
6. 一个钝角三角形中两个锐角和小于90。 ( )
7. 一个三角形中至少有两个锐角。 ( )
√
×
×
×
√
√
√
求下面图形的周长。
6cm
4cm
在一个钝角三角形中,有一个角是40°,剩下两角,较大的锐角是较小锐角的6倍。求另两个角分别是是多少?
巩固练习
1、一个等腰三角形的周长是18厘米,底边长8厘米,它的腰长( )厘米。
2、一个等腰三角形的顶角是50°,那么它的一个底角是( )
3、用一根58厘米长的铁丝围成一个等腰三角形,如果它的底边是14厘米,那么它的一条腰是( )厘米。
4、已知∠1和∠2是直角三角形中的两个锐角。
(1)∠1=35°,∠2=( )
(2)∠1=47°,∠2=( )
5、一个等腰三角形的底边长10厘米,腰比底短3厘米,这个三角形的周长是( )厘米。
6、有四根小棒,长分别是2厘米、3厘米、7厘米和5厘米,选择三根围成一个三角形,围成的三角形的周长是( )厘米。
7、一个等腰三角形的一条边是5厘米,另一条边是4厘米,它的周长是( )厘米或( )厘米。
8、有两根小棒分别是4厘米、7厘米。现在要用第三根小棒(整厘米数)和这两根小棒,围成一个三角形,第三根小棒最短是( )厘米。
9、电动伸缩门就是利用了平行四边形的()的特性。
10、在一个三角形中有两个角都是60°,这个三角形是( )三角形。
11、两个完全一样的直角梯形,可以拼成一个( )
12、一把三角尺上有一个角,其中最大的角是( )角。
13、当梯形的上底和下底相等时,就变成了( )。
14、乐乐拿一根28厘米的彩绳,围成一个等腰三角形,如果底边长10厘米,那么腰长( )厘米。
15、已知等腰三角形三条边长度之和是62厘米,若一条腰长22厘米,则它的底边长( )厘米。
16、一个三角形的三条边都是整厘米数,其中两条边的长度分别为5厘米和9厘米,那么第三条边最长为( )厘米。
17、在一个三角形中,如果两个锐角的和大于90°,那么这个三角形一定是( )三角形。
判断题
1、平行四边形既是特殊的长方形,又是特殊的平行四边形。( )
2、等边三角形一定是锐角三角形。( )
3、90°、43°、57°能围成一个三角形。( )
4、等腰三角形一定不是直角三角形。( )
5、把一个长方形框架拉成平行四边形,这个平行四边形的周长与原来的长方形周长相比变大了。( )
6、有两个角是锐角的三角形一定是锐角三角形。( )
7、红领巾是一个直角三角形。( )
8、等腰三角形一定是锐角三角形。( )
9、三角形的两个内角和小于90°,这个三角形一定是钝角三角形。( )
解决问题
1、一个等腰三角形的周长是35厘米,它的一条腰长是底边长的2倍,它的底底边长是多少厘米?
2、一个三角形的一个内角是32°,另一个内角是105°,第三个内角是多少度?这个三角形是什么三角形?
3、一个平行四边形相邻两条边的和是18厘米,这个平行四边形的周长是多少厘米?
4、如图,小明不小心把一块三角形的玻璃打碎了,你能帮他算出缺少的那个角的度数吗?
5、在一个三角形中,∠1是70°,∠2比∠1大10°,∠3是多少度?
6、在一个三角形的三个内角分别是∠1、∠2、∠3,并且34°+∠1=80°,∠1+∠2=102°,求∠1、∠2和∠3.
认识图形
图形的分类
三角形分类
三角形内角和
三角形边的关系
四边形分类
数图形中的学问
图形的分类
立体图形
平面图形
由线段围成的图形
由曲线围成的图形
三角形具有稳定性。
四边形具有不稳定性。
练习题
1、平行四边形容易( ),三角形具有( )。
2、三角形是( )图形,球形是( )图形。
3、由四条线段组成的图形是四边形 。( )
三角形分类
按角分类
按边分类
锐角三角形
直角三角形
钝角三角形
等腰三角形
等边三角形
不等边三角形
三个角都是锐角
有一个角是直角
有一个角是钝角
有两条边相等
三条边都相等
三条边各不相等
等边三角形是特殊的等腰三角形
等腰三角形
顶角
底角
底角
腰
腰
底边
等边三角形
边
1.找一找,填一填。
图形 是等腰三角形,
图形 是等边三角形,
图形 是直角三角形,
图形 是钝角三角形,
图形 是锐角三角形。
④ ⑤ ⑧ ⑨
⑥ ⑦
③ ⑧
② ⑨
① ④ ⑤ ⑥ ⑦ ⑩
巩固练习
填空题
1、由一个角是( )角的三角形叫做直角三角形。
2、有一个角是钝角三角形叫做( )
3、由三条线段( )的图形叫做三角形。
4、三角形有三条( )和( )个角。
5、( )的三角形叫做锐角三角形。
6、一个三角形中至少有( )个锐角,最多有( )个锐角。
7、三角形按角分为( )三角形、( )三角形和( )三角形。
8、等边三角形又叫( )三角形,它的三条边都( )。
9、等腰三角形两腰间的夹角是( ),腰与底边的夹角是( )。
2、判断:(用手势表示)
(1)、有一个角是锐角的三角形是锐角三角形。
(3)、所有的等腰三角形都是锐角三角形。
(4)、等腰三角形是特殊的等边三角形。
×
×
( )
( )
(2)、所有的等边三角形都是锐角三角形。
( )
√
(5)、有一个角是直角的三角形就叫做直角三角形。
( )
√
( )
×
(6)一个三角形里有两个锐角,必定是锐角三角形。( )
(7)一个三角形里至少有两个锐角。( )
(8)等边三角形都是等腰三角形。( )
(9)在所有的钝角三角形中,不可能有等腰三角形。( )
×
√
√
×
选择题
1、锐角三角形有( )
A、两个锐角 B、一个锐角 C、三个锐角
2、三角形中的一个角是100°,这个三角形是( )三角形。
A、锐角 B、直角 C、钝角
3、一个最小的锐角是50°,这个三角形一定是( )
A、钝角 B、直角 C、锐角
4、一个三角形,其中两个角的平均度数是45°,这个三角形是( )三角形
A、锐角 B、直角 C、钝角
解决问题
1、小亮用3米长的铁丝做了一个等边三角形形状的风筝。风筝的边长是6分米,铁丝剩下多少米?
2、小强想用2米长的铁丝做一个等腰三角形形状的风筝。风筝的腰长是6分米,它的底边长是多少分米?
思考题:
图(1)中分别有( )个锐角三角形,( )个钝角三角形,( )个直角三角形。
?
?
图(2)中分别有( )锐角三角形,( )个钝角三角形,( )个直角三角形。
1
2
2
2
2
4
三角形内角和等于180°。
内角
外角
+
=180 °
内角
外角
1
2
外角= ∠1+∠2
三角形的内角和是180 °
四边形的内角和是360 °
180 °×2
五边形的内角和是540 °
180 °×3
六边形的内角和是720 °
180 °×4
选择题
1、三角形内角和是( )
A、180° B、360° C、90°
2、在直角三角形中,一个锐角是30°,另一个锐角是( )。
A、30° B、60° C、90°
3、一个等腰三角形的顶角是60 °,它的底角是( )
A、60° B、45° C、30°
4、把一个三角形从一个顶点用一条直线分成两个三角形,其中一个三角形的内角和是( )
A、90° B、180° C、360°
5、一个三角形有两个角是锐角,则第三个角是( )
A、一定是锐角
B、一定是钝角
C、一定是直角
D、可能是锐角或钝角或直角
判断题
1、三角形越大,内角和就越大。( )
2、等边三角形一定是锐角三角形。( )
3、一个底角是42°的等腰三角形一定是钝角三角形。( )
4、直角三角形的两个锐角和正好等于90°。( )
5、钝角三角形的内角和大于锐角三角形的内角和。( )
6、在钝角三角形中,两个锐角的和大于90°。( )
7、三角形中有一个角是60°,那么这个三角形一定是个锐角三角形。( )
8、一个三角形中一定不可能有两个钝角。( )
9、一个三角形中最多只能有一个直角。( )
10、用一个10倍的放大镜看一个三角形,这个三角形的内角和是1800°。( )
计算下面三角形中角的度数
1、在直角三角形中,一个角是45°,求另一个角。
2、在一个三角形中,一个角是30°,另一个角是60°,求第三个角。
3、在一个三角形中,∠1=130°,∠3=25°,∠2是多少度?
4、一个等腰三角形的顶角是20°,底角是多少度?
算一算,内角和是多少?
两边的差<第三边的长度<两边的和
判断题
1、三角形任意两条边长度的和一定比第三条边大。( )
2、一个三角形,它的三边长度可以分别是3厘米、6厘米、10厘米。( )
3、三角形最长的一条边有可能等于其他两边的和。( )
4、在一个三角形中,较大的角对应的边较长,较长的边对应的角也较大。( )
5、三角形中任意两边之差都小于第三边。( )
6、在三角形中,有两条边都为4厘米,那么第三条边一定大于4厘米。( )
7、用三根同样长的小棒不能围成三角形。( )
判断下面几组线段能围成三角形吗?为什么?
(1)3厘米、4厘米、5厘米
(2)2厘米、4厘米、6厘米
(3)3厘米、6厘米、4厘米、
(4)2厘米、4厘米、8厘米
如果一个三角形的两条边的长分别是4厘米、6厘米,那么第三条边的长应该在什么范围内?
四边形
梯形
平行四边形
长方形
平行四边形
梯形
两组对边分别平行且相等的四边形,叫做平行四边形。
只有一组对边平行的四边形,叫做梯形。
1、等腰三角形的一个顶角是48 °,它的一个底角是( )
2、( )形和( )形是特殊的平行四边形。
3、两个完全相同的直角三角形,可以拼成( )形。
4、如果将长方形的对角用力拉后,此长方形就变成了 ( )形。
5、一个三角形的两条边分别是9厘米和13厘米,第三条边必须比( )厘米大,比( )厘米小。
填空:
61°
长方
正方
正方形、长方形
平行四边
4
22
二、我是公正的小法官。(对的打“√”,错的打“×”)
1. 等边三角形也是等腰三角形。 ( )
2. 所有三角形的内角和都相等。 ( )
3. 等腰三角形不可能是钝角三角形 。 ( )
4. 把任意一个三角形放在放大镜下,就成了钝角三角形。 ( )
5.平行四边形也是特殊的梯形. ( )
6. 一个钝角三角形中两个锐角和小于90。 ( )
7. 一个三角形中至少有两个锐角。 ( )
√
×
×
×
√
√
√
求下面图形的周长。
6cm
4cm
在一个钝角三角形中,有一个角是40°,剩下两角,较大的锐角是较小锐角的6倍。求另两个角分别是是多少?
巩固练习
1、一个等腰三角形的周长是18厘米,底边长8厘米,它的腰长( )厘米。
2、一个等腰三角形的顶角是50°,那么它的一个底角是( )
3、用一根58厘米长的铁丝围成一个等腰三角形,如果它的底边是14厘米,那么它的一条腰是( )厘米。
4、已知∠1和∠2是直角三角形中的两个锐角。
(1)∠1=35°,∠2=( )
(2)∠1=47°,∠2=( )
5、一个等腰三角形的底边长10厘米,腰比底短3厘米,这个三角形的周长是( )厘米。
6、有四根小棒,长分别是2厘米、3厘米、7厘米和5厘米,选择三根围成一个三角形,围成的三角形的周长是( )厘米。
7、一个等腰三角形的一条边是5厘米,另一条边是4厘米,它的周长是( )厘米或( )厘米。
8、有两根小棒分别是4厘米、7厘米。现在要用第三根小棒(整厘米数)和这两根小棒,围成一个三角形,第三根小棒最短是( )厘米。
9、电动伸缩门就是利用了平行四边形的()的特性。
10、在一个三角形中有两个角都是60°,这个三角形是( )三角形。
11、两个完全一样的直角梯形,可以拼成一个( )
12、一把三角尺上有一个角,其中最大的角是( )角。
13、当梯形的上底和下底相等时,就变成了( )。
14、乐乐拿一根28厘米的彩绳,围成一个等腰三角形,如果底边长10厘米,那么腰长( )厘米。
15、已知等腰三角形三条边长度之和是62厘米,若一条腰长22厘米,则它的底边长( )厘米。
16、一个三角形的三条边都是整厘米数,其中两条边的长度分别为5厘米和9厘米,那么第三条边最长为( )厘米。
17、在一个三角形中,如果两个锐角的和大于90°,那么这个三角形一定是( )三角形。
判断题
1、平行四边形既是特殊的长方形,又是特殊的平行四边形。( )
2、等边三角形一定是锐角三角形。( )
3、90°、43°、57°能围成一个三角形。( )
4、等腰三角形一定不是直角三角形。( )
5、把一个长方形框架拉成平行四边形,这个平行四边形的周长与原来的长方形周长相比变大了。( )
6、有两个角是锐角的三角形一定是锐角三角形。( )
7、红领巾是一个直角三角形。( )
8、等腰三角形一定是锐角三角形。( )
9、三角形的两个内角和小于90°,这个三角形一定是钝角三角形。( )
解决问题
1、一个等腰三角形的周长是35厘米,它的一条腰长是底边长的2倍,它的底底边长是多少厘米?
2、一个三角形的一个内角是32°,另一个内角是105°,第三个内角是多少度?这个三角形是什么三角形?
3、一个平行四边形相邻两条边的和是18厘米,这个平行四边形的周长是多少厘米?
4、如图,小明不小心把一块三角形的玻璃打碎了,你能帮他算出缺少的那个角的度数吗?
5、在一个三角形中,∠1是70°,∠2比∠1大10°,∠3是多少度?
6、在一个三角形的三个内角分别是∠1、∠2、∠3,并且34°+∠1=80°,∠1+∠2=102°,求∠1、∠2和∠3.
