北师大版九年级下册数学:第二章二次函数复习课件(共23张PPT)
文档属性
| 名称 | 北师大版九年级下册数学:第二章二次函数复习课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-29 17:39:52 | ||
图片预览






文档简介
(共23张PPT)
1、二次函数的定义
2、二次函数的图象及性质
3、求解析式的三种方法
4、a,b,c及相关符号的确定
5、二次函数图象的平移?
6、二次函数与一元二次方程的关系?
7、二次函数的应用题
??8、二次函数的综合运用?
二次函数知识点导航:
1、二次函数的定义
练习:
1、y=
2x?
,y=100-5
x?,
,
y=3
x?-2x?+5,
其中是二次函数的有____个。
定义:
y=ax?
+
bx
+
c
(
a、b、c是常数,a
≠
0
)
定义要点:①a
≠
0
②最高次数为2
③代数式一定是整式
2.当m_______时,函数y=(m+1)x
-
2χ+1
是二次函数?
2
=2
知识点
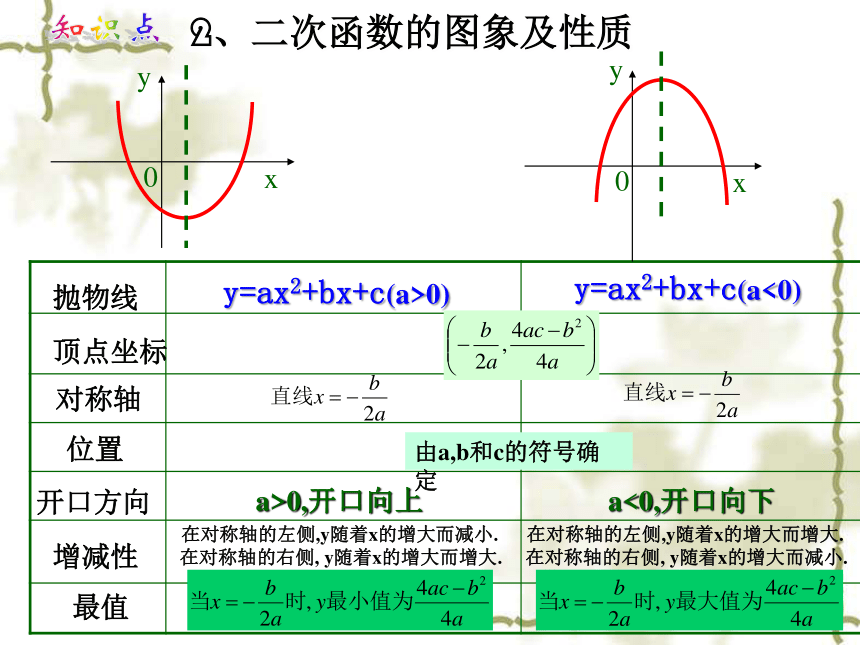
2、二次函数的图象及性质
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
a>0,开口向上
a<0,开口向下
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
知识点
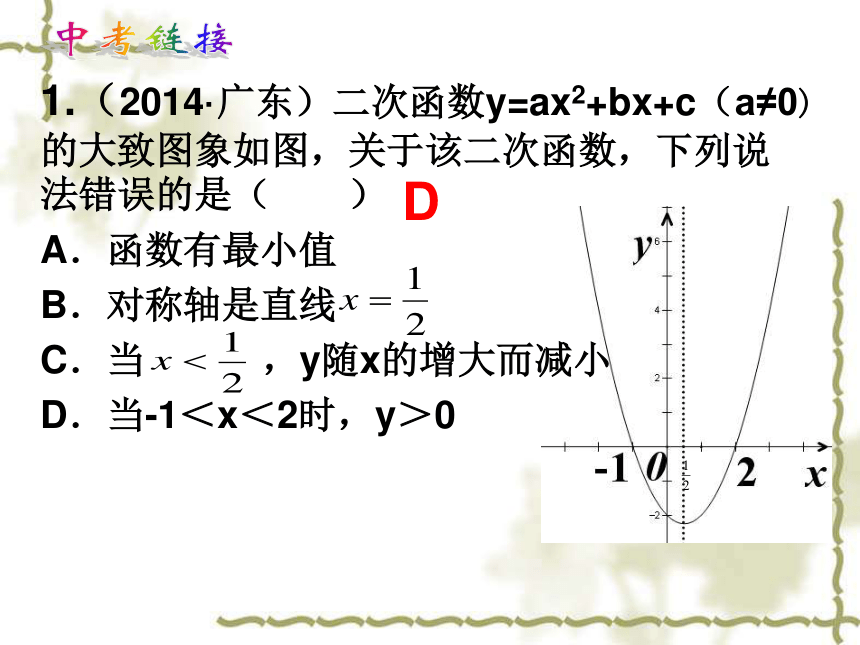
1.(2014·广东)二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
A.函数有最小值
B.对称轴是直线
C.当
,y随x的增大而减小
D.当-1<x<2时,y>0
D
中考链接
2.(2015·广州)已知二次函数y=2(x-3)2+1.下列说法:①其图象的开口向下;
②其图象的对称轴为直线x=-3;
③其图象的顶点坐标为(3,-1);
④当x<3时,y随x的增大而减小.
⑤
若点(
4,b
)与点(
5,d
)在此函数图像上时,b
>
d
,
则其中说法正确的有( )
A.
1个
B.2个
C
.
3个
D.4个
A
中考链接
√
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,(A在B的左侧),求A,B,C的坐标。
(3)x怎样时,y随x的增大而减少;x取多少时,y有最值,这个最值是多少?
(4)x为何值时,y<0?x为何值时,y>0?
1.已知二次函数
直线x=
-1
开口向上
M(-1,-2)
A(-3,0)
B(1,0)
习题
x<-1
0
?
(-1,-2)
?
?
(0,-–)
?
?
(-3,0)
(1,0)
3
2
y
x
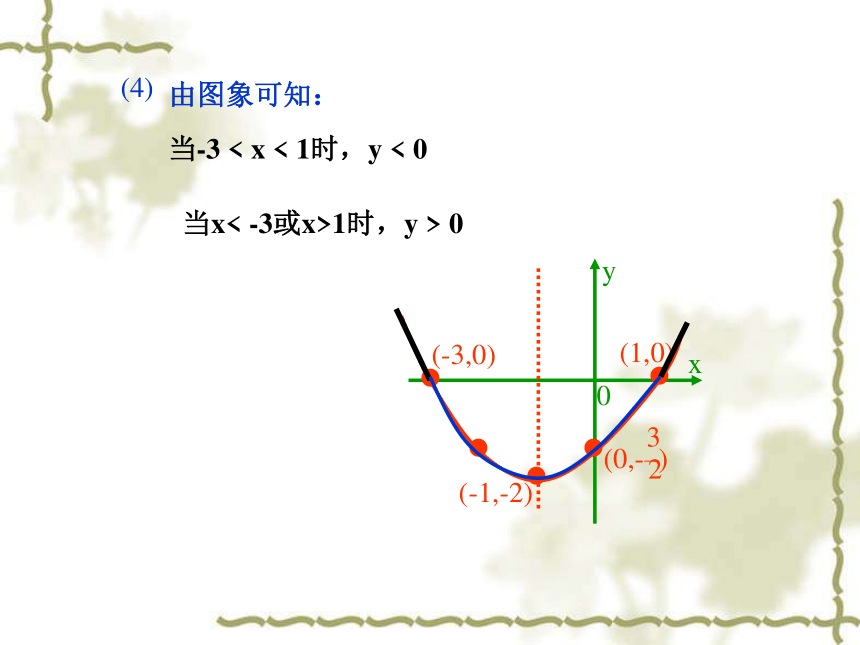
由图象可知:
当x<
-3或x>1时,y
>
0
当-3
<
x
<
1时,y
<
0
(4)
(2)顶点式:已知抛物线顶点坐标(h,
k),通常设抛物线解析式为_______________
求出表达式后化为一般形式.
(3)交点式:已知抛物线与x
轴的两个交点(x1,0)、
(x2,0),通常设解析式为_____________
求出表达式后化为一般形式.
(1)一般式:已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x-h)2+k(a≠0)
y=a(x-x1)(x-x2)
(a≠0)
3、求抛物线解析式的三种方法
知识点
1.根据下列条件,选求二次函数的解析式。
(1)、图象经过(0,0),
(1,-2)
,
(2,3)
三点;
(2)、图象的顶点(2,3),
且经过点(3,1)
;
(3)、图象经过(0,0),
(12,0)
,且最高点
的纵坐标是3
。
习题
(一般式)
(顶点式)
(交点式)
2.如图所示,二次函数y=
ax2+bx+c的图象经过A(2,0)、B(-6,0)、C(0,3),求此函数的表达式。
解:①(交点式)
②(一般式)
③(顶点式)
习题
交点式:
解:∵抛物线与x轴相交的两个点的坐标为(2,0)(-6,0),可设该函数的解析式为:y=a(x+6)(x-2),
∴把点(0,3)代入得:
3=
-12a
∴a=
∴二次函数的解析式为:
一般式:
解:依题意把点(2,0)(-6,0)(0,3)
可得:
4a+2b+c=0
c=3
36a-6b+c=0
解得:
a=
b=
-1
c=3
所以二次函数的解析式为:
顶点式:
解:∵二次函数的对称轴为x=-2,所以可设函数的解析式为:y=a(x+2)2+k,
∴把点(2,0)(0,3)代入可得:
16a+k=0
4a+k=3
解得
a=
k=4
∴
二次函数的解析式为:
3.已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6),求a、b、c。
解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1
∴顶点坐标为(
1
,
2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a
(3-1)2+2
∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即:
y=-2x2+4x,
∴a=-2,b=4,c=0
习题
4、
a.b.c符号的确定
抛物线y=ax2+bx+c的符号问题:
(1)a的符号:
抛物线的开口方向
开口向上
a>0
开口向下
a<0
(2)C的符号:
抛物线与y轴的交点位置
.
交点在y轴正半轴
c>0
交点在y轴负半轴
c<0
经过坐标原点
c=0
知识点
(3)b的符号:
对称轴的位置
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)△的符号:(b2
-
4ac)
抛物线与x轴的交点个数
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
(左同、右异)
1、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c的符号为( )
A、a<0,b>0,c>0,△=0
B、a<0,b>0,c<0,△>0
C、a<0,b<0,c>0,△>0
D、a<0,b<0,c<0,△<0
B
o
熟练掌握a,b,
c,△与抛物线图象的关系
(上正、下负)
(左同、右异)
·
c
习题
2.(2016·深圳)二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①
abc>0
;②
b2
-
4ac<0;
③
b+2a<0;④
a+b+c>0。其中所有正确结论的序号是(
)
A.
③④
B.
②③
C.
①④
D.
①②③
a<0,b>0,c>0
b+2a<0
2a<-b
A
中考链接
(2013·广东)已知二次函数y=x2﹣2mx+m2﹣1。
(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;
中考链接
(3)在(2)的条件下,x轴上是否存在一点P,
使得PC+PD最短?若P点存在,求出P点的坐标;
若P点不存在,请说明理由.
变
1:(4)在(2)的条件下,x轴上是否存在一点P,使得PC+PD的值最小?若存在,求PC+PD的最小值;若不存在,请说明理由.
变
2:(5)如图,在(2)的条件下,A、B为抛物线与x轴的交点,点F为抛物线对称轴上的一个动点,
若FA+FC的值最小,求点F的坐标。
F
P
总复习P60页
y=x2﹣4x+3
C(0,3),D(2,-1)
(1)二次函数图象及性质的应用
(2)二次函数中的符号问题
(3)二次函数解析式的求法
课堂小结:
(2017·广东)如图,在平面直角坐标系中,抛物线y=-x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C。
(1)求抛物线y=-x2+ax+b的解析式;
(2)当点P是线段BC的中点时求点P的坐标;
(3)在(2)的条件下,求sin∠OCB的值。
中考链接
作业:
中考总复习:P62页
第15课时
二次函数
1、二次函数的定义
2、二次函数的图象及性质
3、求解析式的三种方法
4、a,b,c及相关符号的确定
5、二次函数图象的平移?
6、二次函数与一元二次方程的关系?
7、二次函数的应用题
??8、二次函数的综合运用?
二次函数知识点导航:
1、二次函数的定义
练习:
1、y=
2x?
,y=100-5
x?,
,
y=3
x?-2x?+5,
其中是二次函数的有____个。
定义:
y=ax?
+
bx
+
c
(
a、b、c是常数,a
≠
0
)
定义要点:①a
≠
0
②最高次数为2
③代数式一定是整式
2.当m_______时,函数y=(m+1)x
-
2χ+1
是二次函数?
2
=2
知识点
2、二次函数的图象及性质
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
a>0,开口向上
a<0,开口向下
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
知识点
1.(2014·广东)二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
A.函数有最小值
B.对称轴是直线
C.当
,y随x的增大而减小
D.当-1<x<2时,y>0
D
中考链接
2.(2015·广州)已知二次函数y=2(x-3)2+1.下列说法:①其图象的开口向下;
②其图象的对称轴为直线x=-3;
③其图象的顶点坐标为(3,-1);
④当x<3时,y随x的增大而减小.
⑤
若点(
4,b
)与点(
5,d
)在此函数图像上时,b
>
d
,
则其中说法正确的有( )
A.
1个
B.2个
C
.
3个
D.4个
A
中考链接
√
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,(A在B的左侧),求A,B,C的坐标。
(3)x怎样时,y随x的增大而减少;x取多少时,y有最值,这个最值是多少?
(4)x为何值时,y<0?x为何值时,y>0?
1.已知二次函数
直线x=
-1
开口向上
M(-1,-2)
A(-3,0)
B(1,0)
习题
x<-1
0
?
(-1,-2)
?
?
(0,-–)
?
?
(-3,0)
(1,0)
3
2
y
x
由图象可知:
当x<
-3或x>1时,y
>
0
当-3
<
x
<
1时,y
<
0
(4)
(2)顶点式:已知抛物线顶点坐标(h,
k),通常设抛物线解析式为_______________
求出表达式后化为一般形式.
(3)交点式:已知抛物线与x
轴的两个交点(x1,0)、
(x2,0),通常设解析式为_____________
求出表达式后化为一般形式.
(1)一般式:已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x-h)2+k(a≠0)
y=a(x-x1)(x-x2)
(a≠0)
3、求抛物线解析式的三种方法
知识点
1.根据下列条件,选求二次函数的解析式。
(1)、图象经过(0,0),
(1,-2)
,
(2,3)
三点;
(2)、图象的顶点(2,3),
且经过点(3,1)
;
(3)、图象经过(0,0),
(12,0)
,且最高点
的纵坐标是3
。
习题
(一般式)
(顶点式)
(交点式)
2.如图所示,二次函数y=
ax2+bx+c的图象经过A(2,0)、B(-6,0)、C(0,3),求此函数的表达式。
解:①(交点式)
②(一般式)
③(顶点式)
习题
交点式:
解:∵抛物线与x轴相交的两个点的坐标为(2,0)(-6,0),可设该函数的解析式为:y=a(x+6)(x-2),
∴把点(0,3)代入得:
3=
-12a
∴a=
∴二次函数的解析式为:
一般式:
解:依题意把点(2,0)(-6,0)(0,3)
可得:
4a+2b+c=0
c=3
36a-6b+c=0
解得:
a=
b=
-1
c=3
所以二次函数的解析式为:
顶点式:
解:∵二次函数的对称轴为x=-2,所以可设函数的解析式为:y=a(x+2)2+k,
∴把点(2,0)(0,3)代入可得:
16a+k=0
4a+k=3
解得
a=
k=4
∴
二次函数的解析式为:
3.已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6),求a、b、c。
解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1
∴顶点坐标为(
1
,
2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a
(3-1)2+2
∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即:
y=-2x2+4x,
∴a=-2,b=4,c=0
习题
4、
a.b.c符号的确定
抛物线y=ax2+bx+c的符号问题:
(1)a的符号:
抛物线的开口方向
开口向上
a>0
开口向下
a<0
(2)C的符号:
抛物线与y轴的交点位置
.
交点在y轴正半轴
c>0
交点在y轴负半轴
c<0
经过坐标原点
c=0
知识点
(3)b的符号:
对称轴的位置
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)△的符号:(b2
-
4ac)
抛物线与x轴的交点个数
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
(左同、右异)
1、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c的符号为( )
A、a<0,b>0,c>0,△=0
B、a<0,b>0,c<0,△>0
C、a<0,b<0,c>0,△>0
D、a<0,b<0,c<0,△<0
B
o
熟练掌握a,b,
c,△与抛物线图象的关系
(上正、下负)
(左同、右异)
·
c
习题
2.(2016·深圳)二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①
abc>0
;②
b2
-
4ac<0;
③
b+2a<0;④
a+b+c>0。其中所有正确结论的序号是(
)
A.
③④
B.
②③
C.
①④
D.
①②③
a<0,b>0,c>0
b+2a<0
2a<-b
A
中考链接
(2013·广东)已知二次函数y=x2﹣2mx+m2﹣1。
(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;
中考链接
(3)在(2)的条件下,x轴上是否存在一点P,
使得PC+PD最短?若P点存在,求出P点的坐标;
若P点不存在,请说明理由.
变
1:(4)在(2)的条件下,x轴上是否存在一点P,使得PC+PD的值最小?若存在,求PC+PD的最小值;若不存在,请说明理由.
变
2:(5)如图,在(2)的条件下,A、B为抛物线与x轴的交点,点F为抛物线对称轴上的一个动点,
若FA+FC的值最小,求点F的坐标。
F
P
总复习P60页
y=x2﹣4x+3
C(0,3),D(2,-1)
(1)二次函数图象及性质的应用
(2)二次函数中的符号问题
(3)二次函数解析式的求法
课堂小结:
(2017·广东)如图,在平面直角坐标系中,抛物线y=-x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C。
(1)求抛物线y=-x2+ax+b的解析式;
(2)当点P是线段BC的中点时求点P的坐标;
(3)在(2)的条件下,求sin∠OCB的值。
中考链接
作业:
中考总复习:P62页
第15课时
二次函数
