北师大版九年级下册数学:第二章 二次函数回顾与思考课件 (共15张PPT)
文档属性
| 名称 | 北师大版九年级下册数学:第二章 二次函数回顾与思考课件 (共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-01 23:26:30 | ||
图片预览


文档简介
(共15张PPT)
回顾与思考(一)
第二章
二次函数
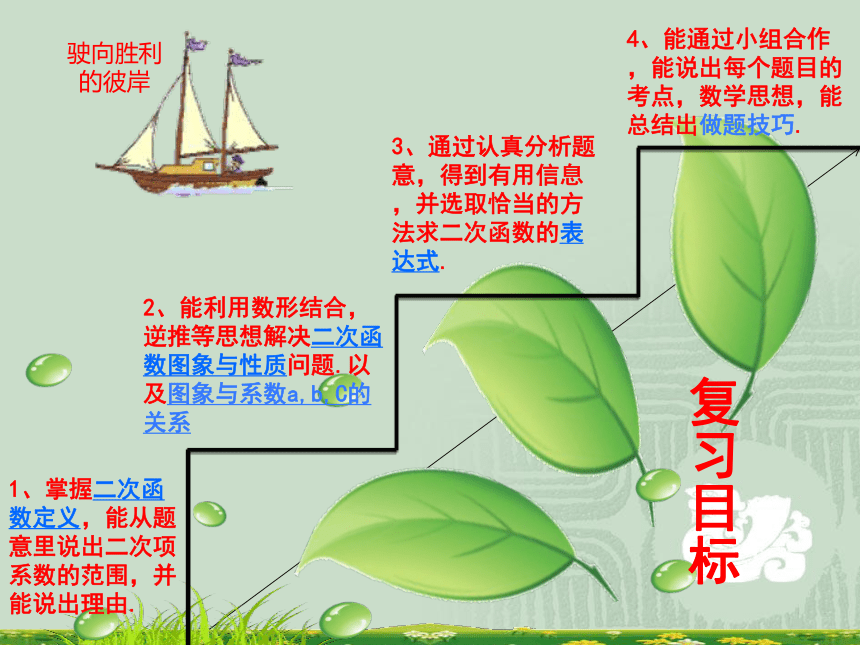
1、掌握二次函数定义,能从题意里说出二次项系数的范围,并能说出理由.
2、能利用数形结合,逆推等思想解决二次函数图象与性质问题.以及图象与系数a,b,C的关系
3、通过认真分析题意,得到有用信息,并选取恰当的方法求二次函数的表达式.
4、能通过小组合作,能说出每个题目的考点,数学思想,能总结出做题技巧.
复习目标
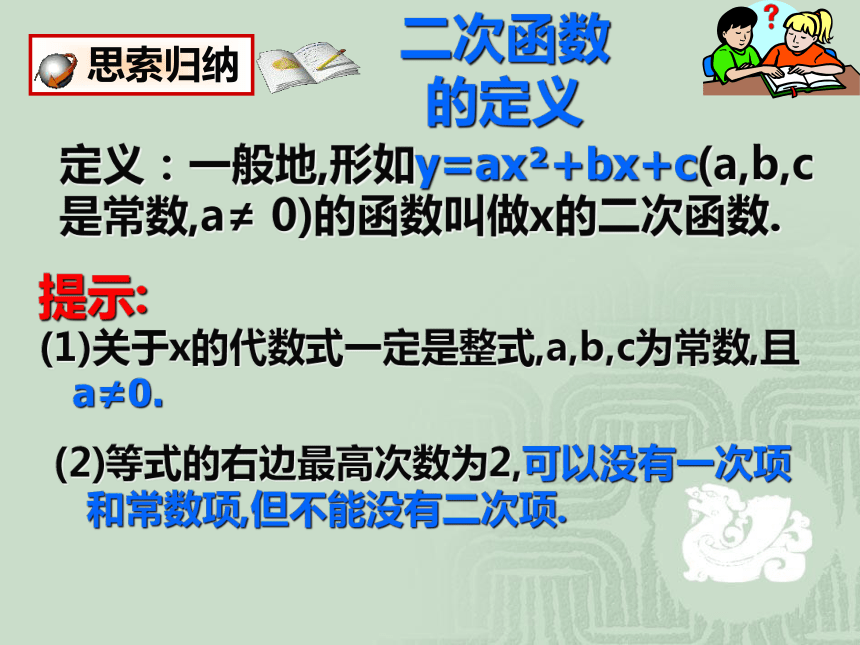
二次函数的定义
定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠
0)的函数叫做x的二次函数.
提示:
(1)关于x的代数式一定是整式,a,b,c为常数,且
a≠0.
(2)等式的右边最高次数为2,可以没有一次项
和常数项,但不能没有二次项.
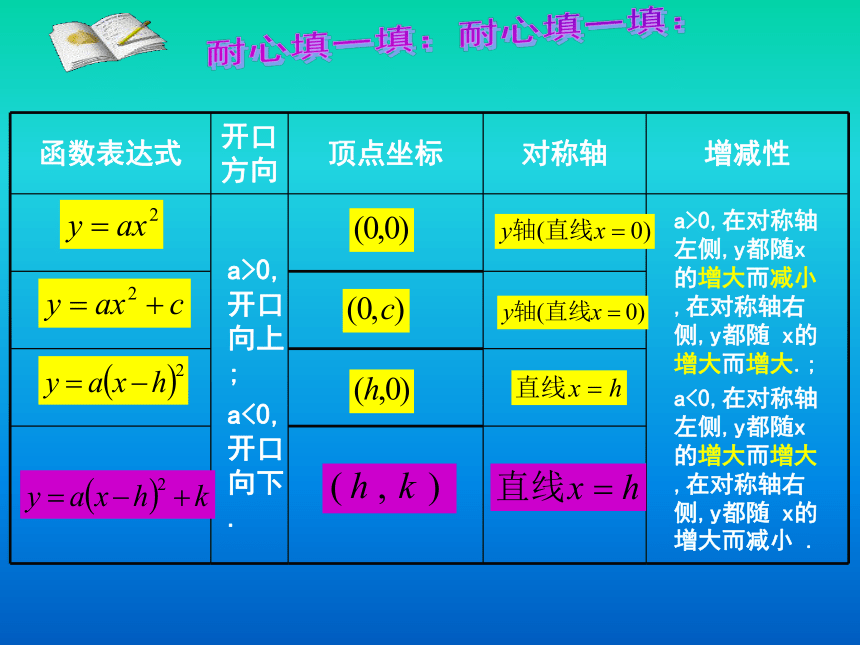
耐心填一填:
a>0,开口向上;
a<0,开口向下.
a>0,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随
x的增大而增大.;
a<0,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随
x的增大而减小
.
函数表达式
开口方向
顶点坐标
对称轴
增减性
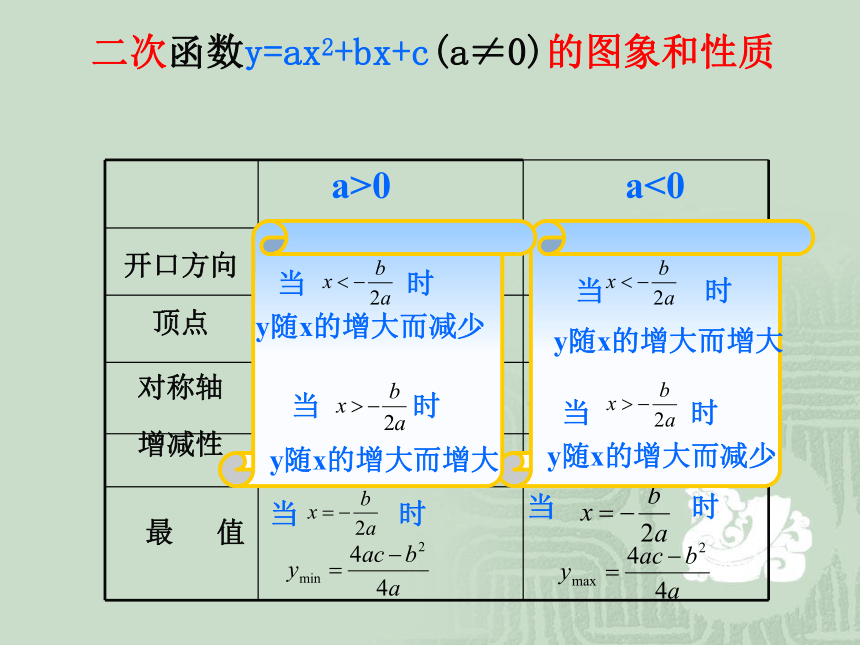
a>0
a<0
开口方向
向上
向下
顶点
对称轴
增减性
最
值
二次函数y=ax2+bx+c(a≠0)的图象和性质
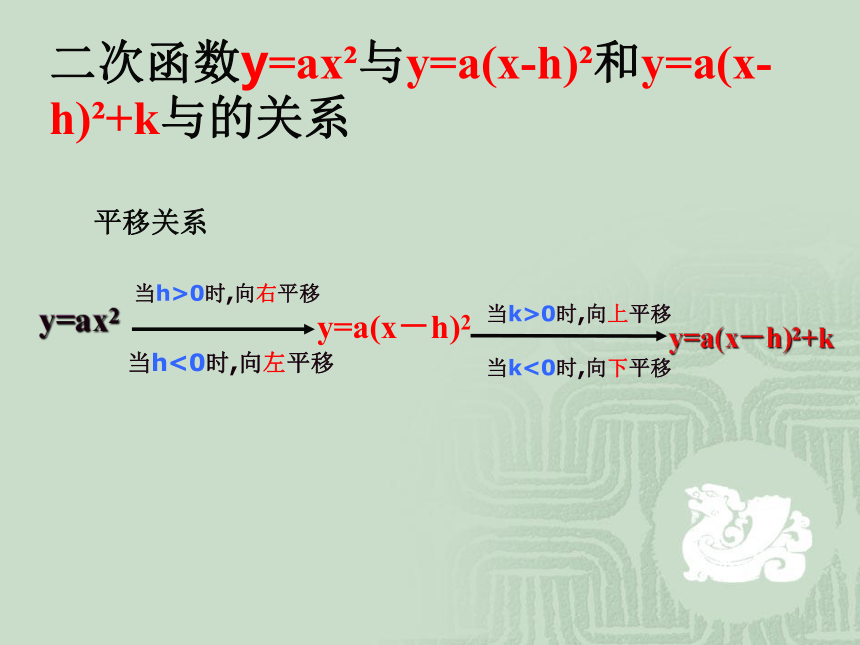
平移关系
当h>0时,向右平移
当h<0时,向左平移
y=ax2
y=a(x-h)2
当k>0时,向上平移
当k<0时,向下平移
y=a(x-h)2+k
二次函数y=ax?与y=a(x-h)?和y=a(x-h)?+k与的关系
2、已知抛物线顶点坐标(h,
k),通常设抛物线解析式为_______________
3、已知抛物线与x
轴的两个交点(x1,0)、
(x2,0),通常设解析式为_____________
1、已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c
(a≠0)
y=a(x-h)2+k
(a≠0)
y=a(x-x1)(x-x2)
(a≠0)
二次函数解析式的三种表示方式
思考:二次函数y=ax2+bx+c
(a
≠0)的图象与系数a,b,c的关系
知识点1:定义辨析
知识点2:图象与性质
抛物线y=2(x-3)2-2的顶点坐标是?
说说y=2(x-3)2-2的图象是怎样由y=2x2的图象平移得到的?
你还能提出哪些问题?
2.已知二次函数y=ax2+bx+c的图象如图所示,请根据图象判断下列各式的符号:a
0
,
b
0,
c
0
,
a-b+c
0,
a+b+c
0
<
<
>
>
=
知识点3:图象与系数的关系
3.函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是(
)
.
C
点击中考:逆推思想
二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6),求a、b、c。
知识点4:选择恰当的方法求函数解析式
本课知识小结
定义
图象
相关概念
性质和图象以及与a,b,c的符号
开口方向、对称轴、顶点坐标、增减性
解析式的确定
三点式
顶点式
交点式
回顾与思考(一)
第二章
二次函数
1、掌握二次函数定义,能从题意里说出二次项系数的范围,并能说出理由.
2、能利用数形结合,逆推等思想解决二次函数图象与性质问题.以及图象与系数a,b,C的关系
3、通过认真分析题意,得到有用信息,并选取恰当的方法求二次函数的表达式.
4、能通过小组合作,能说出每个题目的考点,数学思想,能总结出做题技巧.
复习目标
二次函数的定义
定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠
0)的函数叫做x的二次函数.
提示:
(1)关于x的代数式一定是整式,a,b,c为常数,且
a≠0.
(2)等式的右边最高次数为2,可以没有一次项
和常数项,但不能没有二次项.
耐心填一填:
a>0,开口向上;
a<0,开口向下.
a>0,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随
x的增大而增大.;
a<0,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随
x的增大而减小
.
函数表达式
开口方向
顶点坐标
对称轴
增减性
a>0
a<0
开口方向
向上
向下
顶点
对称轴
增减性
最
值
二次函数y=ax2+bx+c(a≠0)的图象和性质
平移关系
当h>0时,向右平移
当h<0时,向左平移
y=ax2
y=a(x-h)2
当k>0时,向上平移
当k<0时,向下平移
y=a(x-h)2+k
二次函数y=ax?与y=a(x-h)?和y=a(x-h)?+k与的关系
2、已知抛物线顶点坐标(h,
k),通常设抛物线解析式为_______________
3、已知抛物线与x
轴的两个交点(x1,0)、
(x2,0),通常设解析式为_____________
1、已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c
(a≠0)
y=a(x-h)2+k
(a≠0)
y=a(x-x1)(x-x2)
(a≠0)
二次函数解析式的三种表示方式
思考:二次函数y=ax2+bx+c
(a
≠0)的图象与系数a,b,c的关系
知识点1:定义辨析
知识点2:图象与性质
抛物线y=2(x-3)2-2的顶点坐标是?
说说y=2(x-3)2-2的图象是怎样由y=2x2的图象平移得到的?
你还能提出哪些问题?
2.已知二次函数y=ax2+bx+c的图象如图所示,请根据图象判断下列各式的符号:a
0
,
b
0,
c
0
,
a-b+c
0,
a+b+c
0
<
<
>
>
=
知识点3:图象与系数的关系
3.函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是(
)
.
C
点击中考:逆推思想
二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6),求a、b、c。
知识点4:选择恰当的方法求函数解析式
本课知识小结
定义
图象
相关概念
性质和图象以及与a,b,c的符号
开口方向、对称轴、顶点坐标、增减性
解析式的确定
三点式
顶点式
交点式
