1.1.2 探究勾股定理(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 1.1.2 探究勾股定理(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-08 22:27:15 | ||
图片预览


文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第一章勾股定理
1.1
探索勾股定理
第2课时
探索勾股定理(2)
【知识清单】
1.
运用拼图的方法验证勾股定理,关键是利用不同的方法表示相同的面积;
2.
勾股定理是直角三角形特有的性质,非直角三角形不具有此性质.
【经典例题】
例题1、如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.
(1)
若AC=b,BC=a,AB=c,则a、b、c的等量关系为
.
(2)若AC=12,BC=10,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是
.
【考点】勾股定理的证明.
【分析】由题意∠ACB为直角,利用勾股定理
求得外围中一条边,又由AC延伸一倍,从而求
得风车的一个轮子,进一步求得四个.
【解答】(1)图1正方形的面积可表示为c2
①
图1正方形的面积也可表示为4S△ABC+(ab)2
=
4×AC·BC+(ab)2
=4×a·b+(ab)2②
由①②得:c2
=4×a·b+(a-b)2=2ab+a22ab+b2,
∴a2+b2=
c2;
(2)解:设将CA延长到点D,使CA=AD,连接BD,
根据题意,得CD=12×2=24,BC=10.
∵∠BCD=90°,
∴BC2+CD2=BD2,即102+242=BD2,
∴BD=26,∴AD+BD=12+26=38,
∴这个风车的外围周长是38×4=152.
故答案为:152.
【点评】本题是勾股定理在实际情况中应用,并注意隐含的已知条件来解答此类题.
例题2、
如图,将长方形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知AB=8cm,AD=10cm,求AE2的值和图中阴影部分的面积.
【考点】勾股定理;翻折变换(折叠问题).
【分析】注意根据折叠的过程以及长方形的对边相等,
得:AF=AD=BC=10cm,,AB=DC=8cm,,DE=EF.然后
根据勾股定理求得BF的长,再设DE=x,则EC=DCDE=ABDE=(8x)
cm,在Rt△ADE中,
根据勾股定理可以求得AE2的值,也可求得△ADE的面积,进而求解阴影部分的面积.
【解答】由折叠可知△ADE和△AFE关于AE成轴对称,
故AF=AD=10cm,
在Rt△ABF中,BF2=AF2AB2=
10282=36.
所以BF=6,
所以FC=BCBF=ADBF=106=4(cm),
设DE=xcm,则EF=DE=
x
cm,EC=DCEF=(8x)
cm,.
在Rt△EFC中,由勾股定理,得FC2+EC2=EF2,
即42+(8x)2=x2,
解得x=5,故DE=5.
在Rt△ADE
中,AE2=AD2+DE2=
102+52=125.
所以阴影部分的面积为:长方形ABCD的面积减去2倍的△ADE的面积
=
AB·AD2S△ADE=
8×102S△ADE=8050=30(cm2).
【点评】本题主要考查了勾股定理以及折叠变换知识,注意折叠性质的应用,如对应边相等,熟练运用勾股定理进行求解.
【夯实基础】
1、两条边分别为3和4的直角三角形的第三条边长的平方为
( )
A.?25???
B.7???
C.?25或7??
??D.?
16或9
2、一个圆柱型笔筒底面半径为5,高24,则笔筒能容下最长的笔长为( )
A.24
B.26
C.28
D.
32
3、如图,直角三角形三边上的半圆面积从小到大依次记为S?1?、S?2?、S?3,则S?1?、S?2?、S?3?之间的关系是( )
A.S?l?+S?2?>S?3
B.S?l?+S?2?C.S?1?2?+S?2?2?=S?3?2
D.S?1?+S?2?=S?3
4、如图,点C是直线AB上的一点,CD是射线,CE、CF分别是∠ACD和∠BCD的平分线,若EF=7,则CE2+CF2+EF2=(
)
A.98?
B.49???
C.14??
??D.无法确定
5、如图,在矩形ABCD中,AB=6,BC=8,如果将该矩形沿着对角线BD折叠,那么图中阴影
部分的面积为
.
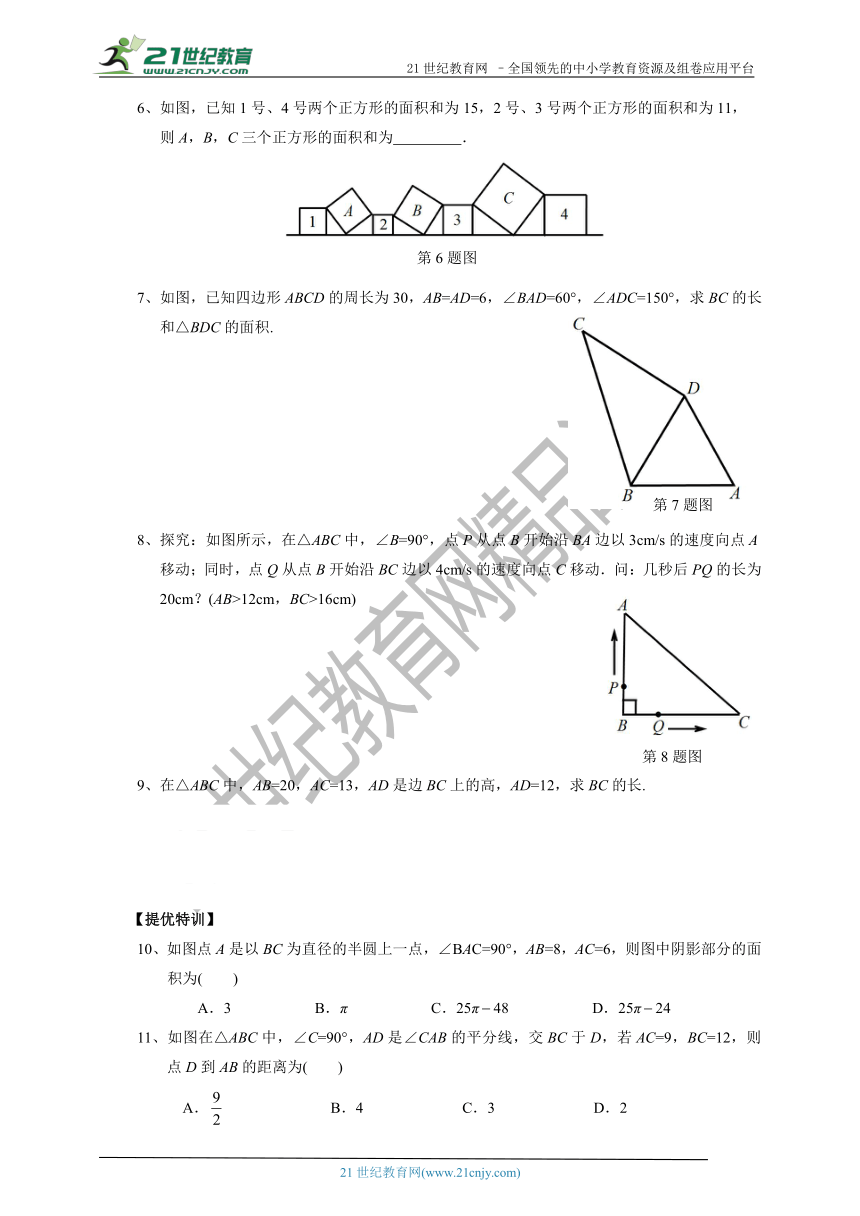
6、如图,已知1号、4号两个正方形的面积和为15,2号、3号两个正方形的面积和为11,
则A,B,C三个正方形的面积和为
.
7、如图,已知四边形ABCD的周长为30,AB=AD=6,∠BAD=60°,∠ADC=150°,求BC的长和△BDC的面积.
8、探究:如图所示,在△ABC中,∠B=90°,点P从点B开始沿BA边以3cm/s的速度向点A移动;同时,点Q从点B开始沿BC边以4cm/s的速度向点C移动.问:几秒后PQ的长为20cm?(AB>12cm,BC>16cm)
9、在△ABC中,AB=20,AC=13,AD是边BC上的高,AD=12,求BC的长.
?
【提优特训】
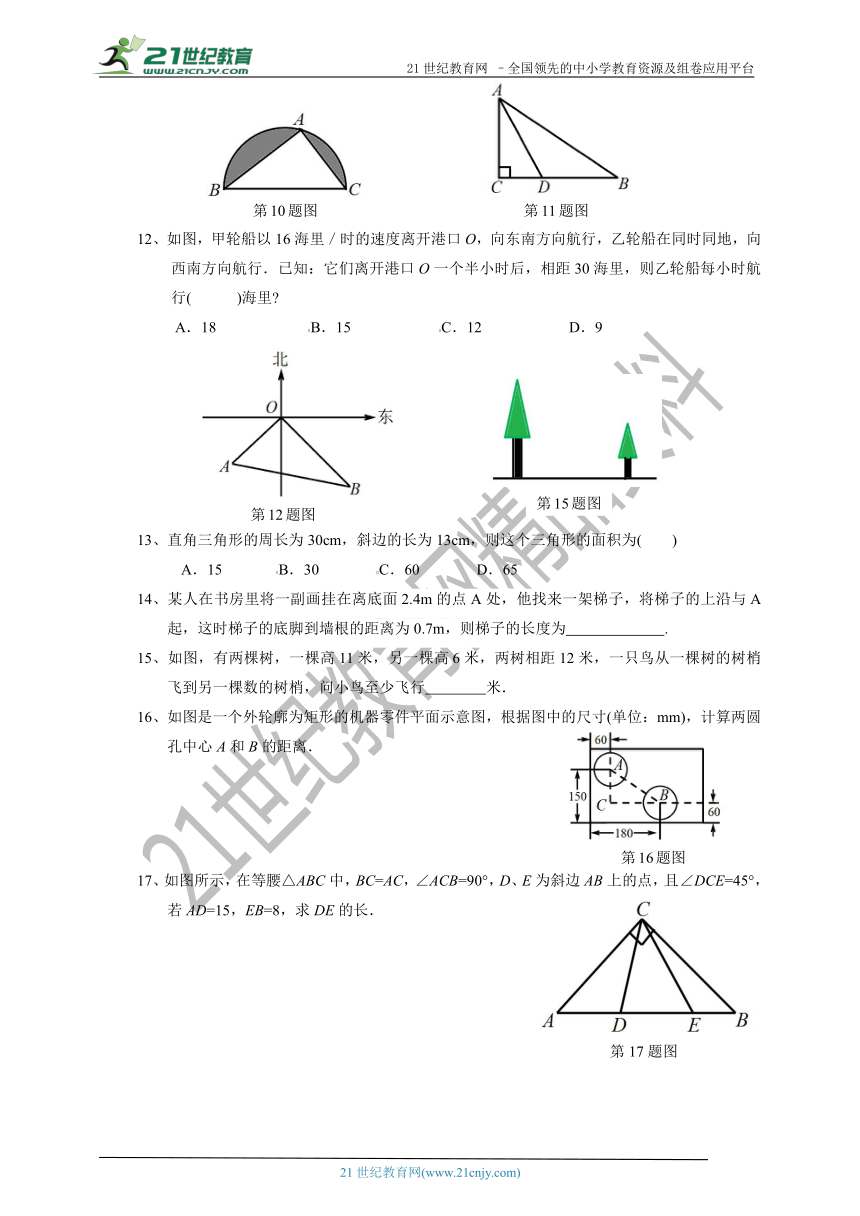
10、如图点A是以BC为直径的半圆上一点,∠BAC=90°,AB=8,AC=6,则图中阴影部分的面积为( )
A.3
B.π
C.25π48
D.25π24
11、如图在△ABC中,∠C=90°,AD是∠CAB的平分线,交BC于D,若AC=9,BC=12,则点D到AB的距离为( )
A.
B.4
C.3
D.2
12、如图,甲轮船以16海里/时的速度离开港口O,向东南方向航行,乙轮船在同时同地,向西南方向航行.已知:它们离开港口O一个半小时后,相距30海里,则乙轮船每小时航行(
)海里?
A.18?????
?B.15????
?
C.12???
?
???D.9
13、直角三角形的周长为30cm,斜边的长为13cm,则这个三角形的面积为(
)
A.15?????
?B.30????
?
C.60???
?
???D.65
14、某人在书房里将一副画挂在离底面2.4m的点A处,他找来一架梯子,将梯子的上沿与A起,这时梯子的底脚到墙根的距离为0.7m,则梯子的长度为
.
15、如图,有两棵树,一棵高11米,另一棵高6米,两树相距12米,一只鸟从一棵树的树梢飞到另一棵数的树梢,问小鸟至少飞行 米.
16、如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离.
17、如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45°,若AD=15,EB=8,求DE的长.
18、在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图1,过点A在△ABC外作直线DE,BD⊥DE于D,CE⊥DE于E.
①判断线段DE、BD、CE之间有何数量关系,并证明;
②若AD=a,BD=b,AB=c,试利用图1验证勾股定理a2+b2=c2;
(2)如图2,过点A在△ABC内作直线DE,BD⊥DE于D,CE⊥DE于E,判断线段DE、
BD、CE之间有何数量关系?(直接写出答案)
【中考链接】
19、(2019?枣庄)
如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE2的长为( )
A.22
B.24
C.44
D.404
20、(2019?宁波)
勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出(??
)?
A.?直角三角形的面积????????????????
??B.?最大正方形的面积
C.?较小两个正方形重叠部分的面积?????
?D.?最大正方形与直角三角形的面积和
参考答案
1、C
2、B
3、D
4、A
5、
6、37
10、D
11、A
12、C
13、B
14、2.5m
15、13
19、B
20、C
7、如图,已知四边形ABCD的周长为30,AB=AD=6,∠BAD=60°,∠ADC=150°,求BC的长和△BDC的面积.
解:∵AB=AD=6,∠BAD=60°,
∴△ABD是等边三角形,
∴∠BDA=∠A=∠BAD=60°,
∴BD=
AB=AD=6,
∵四边形ABCD的周长为30,
∴
DC+CB=四边形ABCD的周长ABAD
=3066=18,
∵∠ADC=150°,∠BDA=60°,
∴∠BDC=∠ADC∠BDA=150°60°=90°.
设BC=x,则DC=18x,
在Rt△BDC中,BC2=BD2+CD2,
∴x2=62+(18x)2,
解得x=10,CD=18x=8,
BC=10.
S△BDC=BD·DC=×6×8=24.
8、探究:如图所示,在△ABC中,∠B=90°,点P从点B开始沿BA边以3cm/s的速度向点A移动;同时,点Q从点B开始沿BC边以4cm/s的速度向点C移动.问:几秒后PQ的长为20cm?(AB>12cm,BC>16cm)
解:设t秒后PQ的长为20cm,
∵点P从点B开始沿BA边以3cm/s的速度向点A移动;
同时,点Q从点B开始沿BC边以4cm/s的速度向点C移动,
∴BP=3t,BQ=4t,
根据题意得:(3t)2+(4t)2=202,
∴t2=16,
∵t>0,
∴t=4,
答:4秒后PQ的长为20cm.
9、在△ABC中,AB=20,AC=13,AD是边BC上的高,AD=12,求BC的长.
?
解:如图1,AD⊥BC于点D,
?
在Rt△ABD,AB=20,AD=12,
BD2=AB2AD2=
202122=256=162,
∴BD=16,
在Rt△ACD,AC=13,AD=12,
CD2=AC2AD2=
132122=25=52,
∴CD=5,
∴BC=BD+DC=16+5=21;
如图2,AD⊥BC的延长线于点D,
?
在Rt△ABD,AB=20,AD=12,
BD2=AB2AD2=
202122=256=162,
∴BD=16,
在Rt△ACD,AC=13,AD=12,
CD2=AC2AD2=
132122=25=52,
∴CD=5,
∴BC=BDDC=165=11.
16、如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离.
解:由图形可知:在△ABC中,∠C=90°
,
AC=150-60=90??
BC=18060=120
?????
??在Rt△ABC中,
根据勾股定理得:AB2=AC2+BC2
????????????
=902+1202?=22500=1502,
所以AB=150?.
答:两圆孔中心的距离150mm.
17、如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45°,若AD=15,EB=8,求DE的长.
证明:如图,将△CAD绕点C逆时针旋转90°到△CBP的位置;
则∠DCP=90°,CD=CP,AD=BP;∠ACD
=∠BCP,∠CBP=∠A;
∵BC=AC,∠ACB=90°,
∴∠A=∠ABC=∠CBP=45°,
∴∠EBP=90°,
∵∠DCE=45°,∠DCP=90°,
∴∠PCE=90°∠DCE=90°45°=45°,
∴∠DCE=∠PCE.
在△DCE与△PCE中,
∵
∴△DCE≌△PCE(SAS)
∴DE=PE.
∵AD=BP=15,EB=8,
在直角三角形PBE中,
∴.
∴PE=17.
18、在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图1,过点A在△ABC外作直线DE,BD⊥DE于D,CE⊥DE于E.
①判断线段DE、BD、CE之间有何数量关系,并证明;
②若AD=a,BD=b,AB=c,试利用图1验证勾股定理a2+b2=c2;
(2)如图2,过点A在△ABC内作直线DE,BD⊥DE于D,CE⊥DE于E,判断线段DE、
BD、CE之间有何数量关系?(直接写出答案)
解:(1)①MN=BM+CN;
理由:∵∠CAB=90°,
∴∠1+∠2=90°,
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
∴∠3+∠2=90°,
∴∠1=∠3,
在△DAB和△ECA中
∵,
∴△DAB≌△ECA(AAS),
∴BD=AE,AD=CE,
∴DE=AD+AE=BD+CE;
②由①知△DAB≌△ECA,
∴CE=AD=a,AE=BD=b,AB=AC=c,
∴DE=a+b,
∵S梯形BCED=S△DAB+S△ABC+S△ECA=ab+c2+ab=ab+c2,
S梯形BCED=((BD+CE)×DE=(a+b)2,
∴(a+b)2=ab+c2,即(a+b)2=2ab+c2,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
(2)DE=CEBD;
理由:∵∠DAB+∠EAC=90°,∠ACE+∠EAC=90°,
∴∠DAB=∠ACE,
在△DAB和△ECA中
∵,
∴△DAB≌△ECA(AAS),
∴BD=AE,AD=CE,
∴DE=ADAE=CEBD.
第8题图
第20题图2
第19题图
第5题图
第3题图
第16题图
第17题图
第9题图1
第18题图2
第18题图1
第9题图2
第20题图1
第15题图
第6题图
第18题图1
第12题图
第11题图
第7题图
第7题图
第4题图
第10题图
第8题图
第16题图
第18题图2
例题2图
第17题图
例题1图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第一章勾股定理
1.1
探索勾股定理
第2课时
探索勾股定理(2)
【知识清单】
1.
运用拼图的方法验证勾股定理,关键是利用不同的方法表示相同的面积;
2.
勾股定理是直角三角形特有的性质,非直角三角形不具有此性质.
【经典例题】
例题1、如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.
(1)
若AC=b,BC=a,AB=c,则a、b、c的等量关系为
.
(2)若AC=12,BC=10,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是
.
【考点】勾股定理的证明.
【分析】由题意∠ACB为直角,利用勾股定理
求得外围中一条边,又由AC延伸一倍,从而求
得风车的一个轮子,进一步求得四个.
【解答】(1)图1正方形的面积可表示为c2
①
图1正方形的面积也可表示为4S△ABC+(ab)2
=
4×AC·BC+(ab)2
=4×a·b+(ab)2②
由①②得:c2
=4×a·b+(a-b)2=2ab+a22ab+b2,
∴a2+b2=
c2;
(2)解:设将CA延长到点D,使CA=AD,连接BD,
根据题意,得CD=12×2=24,BC=10.
∵∠BCD=90°,
∴BC2+CD2=BD2,即102+242=BD2,
∴BD=26,∴AD+BD=12+26=38,
∴这个风车的外围周长是38×4=152.
故答案为:152.
【点评】本题是勾股定理在实际情况中应用,并注意隐含的已知条件来解答此类题.
例题2、
如图,将长方形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知AB=8cm,AD=10cm,求AE2的值和图中阴影部分的面积.
【考点】勾股定理;翻折变换(折叠问题).
【分析】注意根据折叠的过程以及长方形的对边相等,
得:AF=AD=BC=10cm,,AB=DC=8cm,,DE=EF.然后
根据勾股定理求得BF的长,再设DE=x,则EC=DCDE=ABDE=(8x)
cm,在Rt△ADE中,
根据勾股定理可以求得AE2的值,也可求得△ADE的面积,进而求解阴影部分的面积.
【解答】由折叠可知△ADE和△AFE关于AE成轴对称,
故AF=AD=10cm,
在Rt△ABF中,BF2=AF2AB2=
10282=36.
所以BF=6,
所以FC=BCBF=ADBF=106=4(cm),
设DE=xcm,则EF=DE=
x
cm,EC=DCEF=(8x)
cm,.
在Rt△EFC中,由勾股定理,得FC2+EC2=EF2,
即42+(8x)2=x2,
解得x=5,故DE=5.
在Rt△ADE
中,AE2=AD2+DE2=
102+52=125.
所以阴影部分的面积为:长方形ABCD的面积减去2倍的△ADE的面积
=
AB·AD2S△ADE=
8×102S△ADE=8050=30(cm2).
【点评】本题主要考查了勾股定理以及折叠变换知识,注意折叠性质的应用,如对应边相等,熟练运用勾股定理进行求解.
【夯实基础】
1、两条边分别为3和4的直角三角形的第三条边长的平方为
( )
A.?25???
B.7???
C.?25或7??
??D.?
16或9
2、一个圆柱型笔筒底面半径为5,高24,则笔筒能容下最长的笔长为( )
A.24
B.26
C.28
D.
32
3、如图,直角三角形三边上的半圆面积从小到大依次记为S?1?、S?2?、S?3,则S?1?、S?2?、S?3?之间的关系是( )
A.S?l?+S?2?>S?3
B.S?l?+S?2?
D.S?1?+S?2?=S?3
4、如图,点C是直线AB上的一点,CD是射线,CE、CF分别是∠ACD和∠BCD的平分线,若EF=7,则CE2+CF2+EF2=(
)
A.98?
B.49???
C.14??
??D.无法确定
5、如图,在矩形ABCD中,AB=6,BC=8,如果将该矩形沿着对角线BD折叠,那么图中阴影
部分的面积为
.
6、如图,已知1号、4号两个正方形的面积和为15,2号、3号两个正方形的面积和为11,
则A,B,C三个正方形的面积和为
.
7、如图,已知四边形ABCD的周长为30,AB=AD=6,∠BAD=60°,∠ADC=150°,求BC的长和△BDC的面积.
8、探究:如图所示,在△ABC中,∠B=90°,点P从点B开始沿BA边以3cm/s的速度向点A移动;同时,点Q从点B开始沿BC边以4cm/s的速度向点C移动.问:几秒后PQ的长为20cm?(AB>12cm,BC>16cm)
9、在△ABC中,AB=20,AC=13,AD是边BC上的高,AD=12,求BC的长.
?
【提优特训】
10、如图点A是以BC为直径的半圆上一点,∠BAC=90°,AB=8,AC=6,则图中阴影部分的面积为( )
A.3
B.π
C.25π48
D.25π24
11、如图在△ABC中,∠C=90°,AD是∠CAB的平分线,交BC于D,若AC=9,BC=12,则点D到AB的距离为( )
A.
B.4
C.3
D.2
12、如图,甲轮船以16海里/时的速度离开港口O,向东南方向航行,乙轮船在同时同地,向西南方向航行.已知:它们离开港口O一个半小时后,相距30海里,则乙轮船每小时航行(
)海里?
A.18?????
?B.15????
?
C.12???
?
???D.9
13、直角三角形的周长为30cm,斜边的长为13cm,则这个三角形的面积为(
)
A.15?????
?B.30????
?
C.60???
?
???D.65
14、某人在书房里将一副画挂在离底面2.4m的点A处,他找来一架梯子,将梯子的上沿与A起,这时梯子的底脚到墙根的距离为0.7m,则梯子的长度为
.
15、如图,有两棵树,一棵高11米,另一棵高6米,两树相距12米,一只鸟从一棵树的树梢飞到另一棵数的树梢,问小鸟至少飞行 米.
16、如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离.
17、如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45°,若AD=15,EB=8,求DE的长.
18、在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图1,过点A在△ABC外作直线DE,BD⊥DE于D,CE⊥DE于E.
①判断线段DE、BD、CE之间有何数量关系,并证明;
②若AD=a,BD=b,AB=c,试利用图1验证勾股定理a2+b2=c2;
(2)如图2,过点A在△ABC内作直线DE,BD⊥DE于D,CE⊥DE于E,判断线段DE、
BD、CE之间有何数量关系?(直接写出答案)
【中考链接】
19、(2019?枣庄)
如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE2的长为( )
A.22
B.24
C.44
D.404
20、(2019?宁波)
勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出(??
)?
A.?直角三角形的面积????????????????
??B.?最大正方形的面积
C.?较小两个正方形重叠部分的面积?????
?D.?最大正方形与直角三角形的面积和
参考答案
1、C
2、B
3、D
4、A
5、
6、37
10、D
11、A
12、C
13、B
14、2.5m
15、13
19、B
20、C
7、如图,已知四边形ABCD的周长为30,AB=AD=6,∠BAD=60°,∠ADC=150°,求BC的长和△BDC的面积.
解:∵AB=AD=6,∠BAD=60°,
∴△ABD是等边三角形,
∴∠BDA=∠A=∠BAD=60°,
∴BD=
AB=AD=6,
∵四边形ABCD的周长为30,
∴
DC+CB=四边形ABCD的周长ABAD
=3066=18,
∵∠ADC=150°,∠BDA=60°,
∴∠BDC=∠ADC∠BDA=150°60°=90°.
设BC=x,则DC=18x,
在Rt△BDC中,BC2=BD2+CD2,
∴x2=62+(18x)2,
解得x=10,CD=18x=8,
BC=10.
S△BDC=BD·DC=×6×8=24.
8、探究:如图所示,在△ABC中,∠B=90°,点P从点B开始沿BA边以3cm/s的速度向点A移动;同时,点Q从点B开始沿BC边以4cm/s的速度向点C移动.问:几秒后PQ的长为20cm?(AB>12cm,BC>16cm)
解:设t秒后PQ的长为20cm,
∵点P从点B开始沿BA边以3cm/s的速度向点A移动;
同时,点Q从点B开始沿BC边以4cm/s的速度向点C移动,
∴BP=3t,BQ=4t,
根据题意得:(3t)2+(4t)2=202,
∴t2=16,
∵t>0,
∴t=4,
答:4秒后PQ的长为20cm.
9、在△ABC中,AB=20,AC=13,AD是边BC上的高,AD=12,求BC的长.
?
解:如图1,AD⊥BC于点D,
?
在Rt△ABD,AB=20,AD=12,
BD2=AB2AD2=
202122=256=162,
∴BD=16,
在Rt△ACD,AC=13,AD=12,
CD2=AC2AD2=
132122=25=52,
∴CD=5,
∴BC=BD+DC=16+5=21;
如图2,AD⊥BC的延长线于点D,
?
在Rt△ABD,AB=20,AD=12,
BD2=AB2AD2=
202122=256=162,
∴BD=16,
在Rt△ACD,AC=13,AD=12,
CD2=AC2AD2=
132122=25=52,
∴CD=5,
∴BC=BDDC=165=11.
16、如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离.
解:由图形可知:在△ABC中,∠C=90°
,
AC=150-60=90??
BC=18060=120
?????
??在Rt△ABC中,
根据勾股定理得:AB2=AC2+BC2
????????????
=902+1202?=22500=1502,
所以AB=150?.
答:两圆孔中心的距离150mm.
17、如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45°,若AD=15,EB=8,求DE的长.
证明:如图,将△CAD绕点C逆时针旋转90°到△CBP的位置;
则∠DCP=90°,CD=CP,AD=BP;∠ACD
=∠BCP,∠CBP=∠A;
∵BC=AC,∠ACB=90°,
∴∠A=∠ABC=∠CBP=45°,
∴∠EBP=90°,
∵∠DCE=45°,∠DCP=90°,
∴∠PCE=90°∠DCE=90°45°=45°,
∴∠DCE=∠PCE.
在△DCE与△PCE中,
∵
∴△DCE≌△PCE(SAS)
∴DE=PE.
∵AD=BP=15,EB=8,
在直角三角形PBE中,
∴.
∴PE=17.
18、在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图1,过点A在△ABC外作直线DE,BD⊥DE于D,CE⊥DE于E.
①判断线段DE、BD、CE之间有何数量关系,并证明;
②若AD=a,BD=b,AB=c,试利用图1验证勾股定理a2+b2=c2;
(2)如图2,过点A在△ABC内作直线DE,BD⊥DE于D,CE⊥DE于E,判断线段DE、
BD、CE之间有何数量关系?(直接写出答案)
解:(1)①MN=BM+CN;
理由:∵∠CAB=90°,
∴∠1+∠2=90°,
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
∴∠3+∠2=90°,
∴∠1=∠3,
在△DAB和△ECA中
∵,
∴△DAB≌△ECA(AAS),
∴BD=AE,AD=CE,
∴DE=AD+AE=BD+CE;
②由①知△DAB≌△ECA,
∴CE=AD=a,AE=BD=b,AB=AC=c,
∴DE=a+b,
∵S梯形BCED=S△DAB+S△ABC+S△ECA=ab+c2+ab=ab+c2,
S梯形BCED=((BD+CE)×DE=(a+b)2,
∴(a+b)2=ab+c2,即(a+b)2=2ab+c2,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
(2)DE=CEBD;
理由:∵∠DAB+∠EAC=90°,∠ACE+∠EAC=90°,
∴∠DAB=∠ACE,
在△DAB和△ECA中
∵,
∴△DAB≌△ECA(AAS),
∴BD=AE,AD=CE,
∴DE=ADAE=CEBD.
第8题图
第20题图2
第19题图
第5题图
第3题图
第16题图
第17题图
第9题图1
第18题图2
第18题图1
第9题图2
第20题图1
第15题图
第6题图
第18题图1
第12题图
第11题图
第7题图
第7题图
第4题图
第10题图
第8题图
第16题图
第18题图2
例题2图
第17题图
例题1图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
