2020年江苏省高考数学试卷 (word解析版)
文档属性
| 名称 | 2020年江苏省高考数学试卷 (word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 544.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-10 09:29:27 | ||
图片预览




文档简介
2020年江苏省高考数学试卷
一、填空题(共14小题).
1.已知集合A={﹣1,0,1,2},B={0,2,3},则A∩B=
.
2.已知i是虚数单位,则复数z=(1+i)(2﹣i)的实部是
.
3.已知一组数据4,2a,3﹣a,5,6的平均数为4,则a的值是
.
4.将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是
.
5.如图是一个算法流程图,若输出y的值为﹣2,则输入x的值是
.
6.在平面直角坐标系xOy中,若双曲线﹣=1(a>0)的一条渐近线方程为y=x,则该双曲线的离心率是
.
7.已知y=f(x)是奇函数,当x≥0时,f(x)=x,则f(﹣8)的值是
.
8.已知sin2(+α)=,则sin2α的值是
.
9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2cm,高为2cm,内孔半径为0.5cm,则此六角螺帽毛坯的体积是
cm3.
10.将函数y=3sin(2x+)的图象向右平移个单位长度,则平移后的图象中与y轴最近的对称轴的方程是
.
11.设{an}是公差为d的等差数列,{bn}是公比为q的等比数列.已知数列{an+bn}的前n项和Sn=n2﹣n+2n﹣1(n∈N
),则d+q的值是
.
12.已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值是
.
13.在△ABC中,AB=4,AC=3,∠BAC=90°,D在边BC上,延长AD到P,使得AP=9.若=m+(﹣m)(m为常数),则CD的长度是
.
14.在平面直角坐标系xOy中,已知P(,0),A、B是圆C:x2+(y﹣)2=36上的两个动点,满足PA=PB,则△PAB面积的最大值是
.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.在三棱柱ABC﹣A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.
(1)求证:EF∥平面AB1C1;
(2)求证:平面AB1C⊥平面ABB1.
16.在△ABC中,角A、B、C的对边分别为a、b、c.已知a=3,c=,B=45°.
(1)求sinC的值;
(2)在边BC上取一点D,使得cos∠ADC=﹣,求tan∠DAC的值.
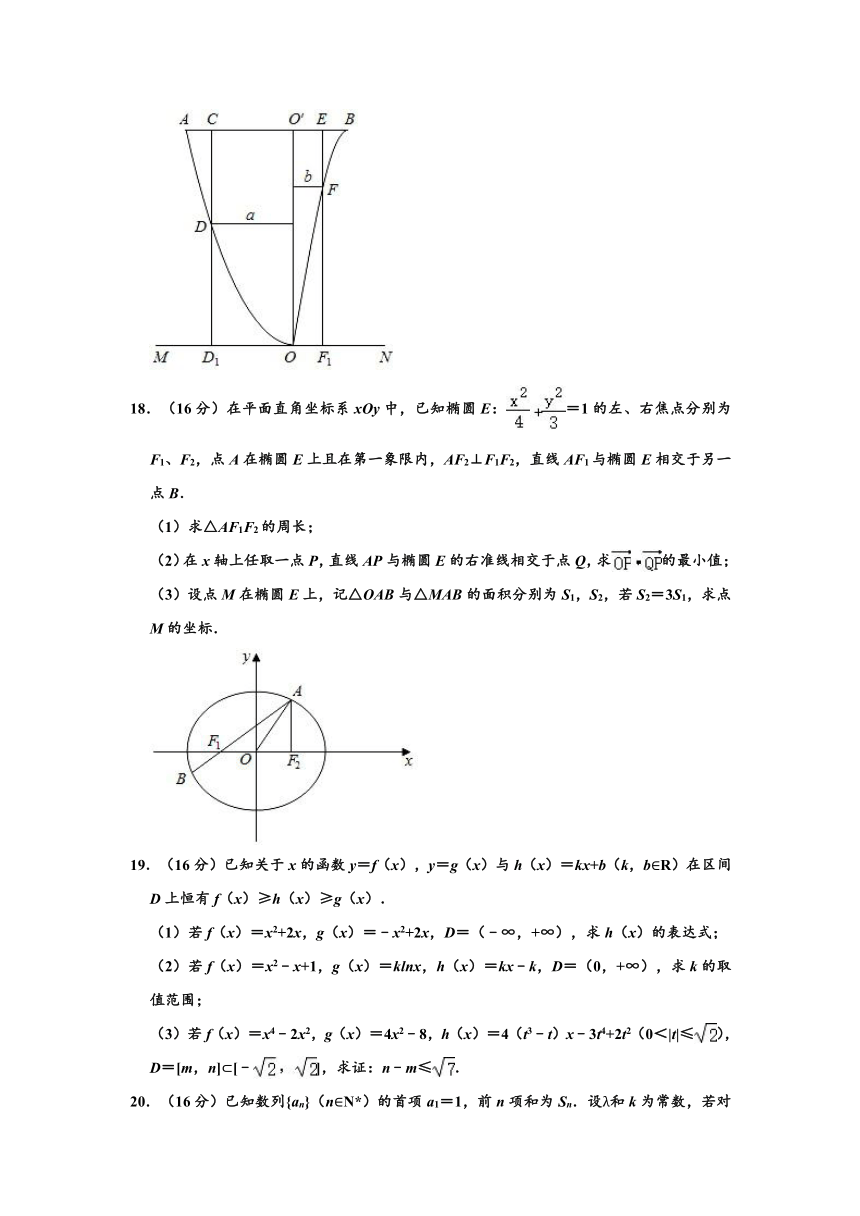
17.某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O在水平线MN上,桥AB与MN平行,OO′为铅垂线(O′在AB上).经测量,左侧曲线AO上任一点D到MN的距离h1(米)与D到OO′的距离a(米)之间满足关系式h1=a2;右侧曲线BO上任一点F到MN的距离h2(米)与F到OO′的距离b(米)之间满足关系式h2=﹣b3+6b.已知点B到OO′的距离为40米.
(1)求桥AB的长度;
(2)计划在谷底两侧建造平行于OO′的桥墩CD和EF,且CE为80米,其中C,E在AB上(不包括端点).桥墩EF每米造价k(万元),桥墩CD每米造价k(万元)(k>0),问O′E为多少米时,桥墩CD与EF的总造价最低?
18.(16分)在平面直角坐标系xOy中,已知椭圆E:=1的左、右焦点分别为F1、F2,点A在椭圆E上且在第一象限内,AF2⊥F1F2,直线AF1与椭圆E相交于另一点B.
(1)求△AF1F2的周长;
(2)在x轴上任取一点P,直线AP与椭圆E的右准线相交于点Q,求的最小值;
(3)设点M在椭圆E上,记△OAB与△MAB的面积分别为S1,S2,若S2=3S1,求点M的坐标.
19.(16分)已知关于x的函数y=f(x),y=g(x)与h(x)=kx+b(k,b∈R)在区间D上恒有f(x)≥h(x)≥g(x).
(1)若f(x)=x2+2x,g(x)=﹣x2+2x,D=(﹣∞,+∞),求h(x)的表达式;
(2)若f(x)=x2﹣x+1,g(x)=klnx,h(x)=kx﹣k,D=(0,+∞),求k的取值范围;
(3)若f(x)=x4﹣2x2,g(x)=4x2﹣8,h(x)=4(t3﹣t)x﹣3t4+2t2(0<|t|≤),D=[m,n]?[﹣],求证:n﹣m≤.
20.(16分)已知数列{an}(n∈N
)的首项a1=1,前n项和为Sn.设λ和k为常数,若对一切正整数n,均有Sn+1﹣Sn=λan+1成立,则称此数列为“λ﹣k”数列.
(1)若等差数列{an}是“λ﹣1”数列,求λ的值;
(2)若数列{an}是“﹣2”数列,且an>0,求数列{an}的通项公式;
(3)对于给定的λ,是否存在三个不同的数列{an}为“λ﹣3”数列,且an≥0?若存在,求出λ的取值范围;若不存在,说明理由.
【选做题】本题包括A、B、C三小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-2:矩阵与变换](本小题满分10分)
21.系统找不到该试题
B.[选修4-4:坐标系与参数方程](本小题满分10分)
22.系统找不到该试题
C.[选修4-5:不等式选讲](本小题满分0分)
23.系统找不到该试题
【必做题】第24题、第25题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
24.系统找不到该试题
25.系统找不到该试题
参考答案
一、填空题:本题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上.
1.已知集合A={﹣1,0,1,2},B={0,2,3},则A∩B= {0,2} .
【分析】运用集合的交集运算,可得所求集合.
解:集合B={0,2,3},A={﹣1,0,1,2},
则A∩B={0,2},
故答案为:{0,2}.
2.已知i是虚数单位,则复数z=(1+i)(2﹣i)的实部是 3 .
【分析】利用复数的乘法的运算法则,化简求解即可.
解:复数z=(1+i)(2﹣i)=3+i,
所以复数z=(1+i)(2﹣i)的实部是:3.
故答案为:3.
3.已知一组数据4,2a,3﹣a,5,6的平均数为4,则a的值是 2 .
【分析】运用平均数的定义,解方程可得a的值.
解:一组数据4,2a,3﹣a,5,6的平均数为4,
则4+2a+(3﹣a)+5+6=4×5,
解得a=2.
故答案为:2.
4.将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是 .
【分析】分别求得基本事件的总数和点数和为5的事件数,由古典概率的计算公式可得所求值.
解:一颗质地均匀的正方体骰子先后抛掷2次,可得基本事件的总数为6×6=36种,
而点数和为5的事件为(1,4),(2,3),(3,2),(4,1),共4种,
则点数和为5的概率为P==.
故答案为:.
5.如图是一个算法流程图,若输出y的值为﹣2,则输入x的值是 ﹣3 .
【分析】由已知中的程序语句可知:该程序的功能是利用程序框图表达式为分段函数计算并输出变量y的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解:由题意可得程序框图表达式为分段函数y=,
若输出y值为﹣2时,由于2x>0,
所以解x+1=﹣2,
即x=﹣3,
故答案为:﹣3,
6.在平面直角坐标系xOy中,若双曲线﹣=1(a>0)的一条渐近线方程为y=x,则该双曲线的离心率是 .
【分析】利用双曲线的渐近线方程,求出a,然后求解双曲线的离心率即可.
解:双曲线﹣=1(a>0)的一条渐近线方程为y=x,可得,所以a=2,
所以双曲线的离心率为:e==,
故答案为:.
7.已知y=f(x)是奇函数,当x≥0时,f(x)=x,则f(﹣8)的值是 ﹣4 .
【分析】由奇函数的定义可得f(﹣x)=﹣f(x),由已知可得f(8),进而得到f(﹣8).
解:y=f(x)是奇函数,可得f(﹣x)=﹣f(x),
当x≥0时,f(x)=x,可得f(8)=8=4,
则f(﹣8)=﹣f(8)=﹣4,
故答案为:﹣4.
8.已知sin2(+α)=,则sin2α的值是 .
【分析】根据二倍角公式即可求出.
解:因为sin2(+α)=,则sin2(+α)===,
解得sin2α=,
故答案为:
9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2cm,高为2cm,内孔半径为0.5cm,则此六角螺帽毛坯的体积是 12 cm3.
【分析】通过棱柱的体积减去圆柱的体积,即可推出结果.
解:六棱柱的体积为:,
圆柱的体积为:π×(0.5)2×2=,
所以此六角螺帽毛坯的体积是:(12)cm3,
故答案为:12.
10.将函数y=3sin(2x+)的图象向右平移个单位长度,则平移后的图象中与y轴最近的对称轴的方程是 x=﹣ .
【分析】利用三角函数的平移可得新函数g(x)=f(x﹣),求g(x)的所有对称轴x=+,k∈Z,从而可判断平移后的图象中与y轴最近的对称轴的方程,
解:因为函数y=3sin(2x+)的图象向右平移个单位长度可得
g(x)=f(x﹣)=3sin(2x﹣+)=3sin(2x﹣),
则y=g(x)的对称轴为2x﹣=+kπ,k∈Z,
即x=+,k∈Z,
当k=0时,x=,
当k=﹣1时,x=,
所以平移后的图象中与y轴最近的对称轴的方程是x=,
故答案为:x=,
11.设{an}是公差为d的等差数列,{bn}是公比为q的等比数列.已知数列{an+bn}的前n项和Sn=n2﹣n+2n﹣1(n∈N
),则d+q的值是 4 .
【分析】由{an+bn}的前n项和Sn=n2﹣n+2n﹣1(n∈N
),由{an}是公差为d的等差数列,设首项为a1;求出等差数列的前n项和的表达式;{bn}是公比为q的等比数列,设首项为b1,讨论当q为1和不为1时的前n项和的表达式,由题意可得q≠1,由对应项的系数相等可得d,q的值,进而求出d+q的值.
解:因为{an+bn}的前n项和Sn=n2﹣n+2n﹣1(n∈N
),
因为{an}是公差为d的等差数列,设首项为a1;{bn}是公比为q的等比数列,设首项为b1,
所以{an}的通项公式an=a1+(n﹣1)d,所以其前n项和S==n2+(a1﹣)n,
当{bn}中,当公比q=1时,其前n项和S=nb1,
所以{an+bn}的前n项和Sn=S+S=n2+(a1﹣)n+nb1=n2﹣n+2n﹣1(n∈N
),显然没有出现2n,所以q≠1,
则{bn}的前n项和为S==+,
所以Sn=S+S=n2+(a1﹣)n+﹣=n2﹣n+2n﹣1(n∈N
),
由两边对应项相等可得:解得:d=2,a1=0,q=2,b1=1,
所以d+q=4,
故答案为:4.
12.已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值是 .
【分析】方法一、由已知求得x2,代入所求式子,整理后,运用基本不等式可得所求最小值;
方法二、由4=(5x2+y2)?4y2,运用基本不等式,计算可得所求最小值.
解:方法一、由5x2y2+y4=1,可得x2=,
由x2≥0,可得y2∈(0,1],
则x2+y2=+y2==(4y2+)
≥?2=,当且仅当y2=,x2=,
可得x2+y2的最小值为;
方法二、4=(5x2+y2)?4y2≤()2=(x2+y2)2,
故x2+y2≥,
当且仅当5x2+y2=4y2=2,即y2=,x2=时取得等号,
可得x2+y2的最小值为.
故答案为:.
13.在△ABC中,AB=4,AC=3,∠BAC=90°,D在边BC上,延长AD到P,使得AP=9.若=m+(﹣m)(m为常数),则CD的长度是 0或 .
【分析】以A为坐标原点,分别以AB,AC所在直线为x,y轴建立平面直角坐标系,求得B与C的坐标,再把的坐标用m表示.由AP=9列式求得m值,然后分类求得D的坐标,则CD的长度可求.
解:如图,以A为坐标原点,分别以AB,AC所在直线为x,y轴建立平面直角坐标系,
则B(4,0),C(0,3),
由=m+(﹣m),得,
整理得:
=﹣2m(4,0)+(2m﹣3)(0,3)=(﹣8m,6m﹣9).
由AP=9,得64m2+(6m﹣9)2=81,解得m=或m=0.
当m=0时,,此时C与D重合,|CD|=0;
当m=时,直线PA的方程为y=x,
直线BC的方程为,
联立两直线方程可得x=m,y=3﹣2m.
即D(,),
∴|CD|=.
∴CD的长度是0或.
故答案为:0或.
14.在平面直角坐标系xOy中,已知P(,0),A、B是圆C:x2+(y﹣)2=36上的两个动点,满足PA=PB,则△PAB面积的最大值是 10 .
【分析】求得圆的圆心C和半径,作PC所在直径EF,交AB于点D,运用垂径定理和勾股定理,以及三角形的面积公式,由三角换元,结合函数的导数,求得单调区间,计算可得所求最大值.
解:圆C:x2+(y﹣)2=36的圆心C(0,),半径为6,
如图,作PC所在直径EF,交AB于点D,
因为PA=PB,CA=CB=R=6,所以PC⊥AB,EF为垂径,
要使面积S△PAB最大,则P,D位于C的两侧,
并设CD=x,可得PC==1,故PD=1+x,AB=2BD=2,
可令x=6cosθ,
S△PAB=|AB|?|PD|=(1+x)=(1+6cosθ)?6sinθ=6sinθ+18sin2θ,0<θ≤,
设函数f(θ)=6sinθ+18sin2θ,0<θ≤,
f′(θ)=6cosθ+36cos2θ=6(12cos2θ+cosθ﹣6),
由f′(θ)=6(12cos2θ+cosθ﹣6)=0,解得cosθ=(cosθ=﹣<0舍去),
显然,当0≤cosθ<,f′(θ)<0,f(θ)递减;当<cosθ<1时,f′(θ)>0,f(θ)递增,
结合cosθ在(0,)递减,故cosθ=时,f(θ)最大,此时sinθ==,
故f(θ)max=6×+36××=10,
则△PAB面积的最大值为10.
故答案为:10.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.在三棱柱ABC﹣A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.
(1)求证:EF∥平面AB1C1;
(2)求证:平面AB1C⊥平面ABB1.
【分析】(1)证明EF∥AB1,然后利用直线与平面平行的判断定理证明EF∥平面AB1C1;
(2)证明B1C⊥AB,结合AB⊥AC,证明AB⊥平面AB1C,然后证明平面AB1C⊥平面ABB1.
【解答】证明:(1)E,F分别是AC,B1C的中点.
所以EF∥AB1,因为EF?平面AB1C1,AB1?平面AB1C1,
所以EF∥平面AB1C1;
(2)因为B1C⊥平面ABC,AB?平面ABB1,
所以B1C⊥AB,
又因为AB⊥AC,AC∩B1C=C,AC?平面AB1C,B1C?平面AB1C,
所以AB⊥平面AB1C,
因为AB?平面ABB1,
所以平面AB1C⊥平面ABB1.
16.在△ABC中,角A、B、C的对边分别为a、b、c.已知a=3,c=,B=45°.
(1)求sinC的值;
(2)在边BC上取一点D,使得cos∠ADC=﹣,求tan∠DAC的值.
【分析】(1)由题意及余弦定理求出b边,再由正弦定理求出sinC的值;
(2)三角形的内角和为180°,cos∠ADC=﹣,可得∠ADC为钝角,可得∠DAC与∠ADC+∠C互为补角,所以sin∠DAC=sin(∠ADC+∠C)展开可得sin∠DAC及cos∠DAC,进而求出tan∠DAC的值.
解:(1)因为a=3,c=,B=45°.,由余弦定理可得:b===,
由正弦定理可得=,所以sinC=?sin45°==,
所以sinC=;
(2)因为cos∠ADC=﹣,所以sin∠ADC==,
在三角形ADC
中,易知C为锐角,由(1)可得cosC==,
所以在三角形ADC中,sin∠DAC=sin(∠ADC+∠C)=sin∠ADCcos∠C+cos∠ADCsin∠C=,
因为∠DAC,所以cos∠DAC==,
所以tan∠DAC==.
17.某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O在水平线MN上,桥AB与MN平行,OO′为铅垂线(O′在AB上).经测量,左侧曲线AO上任一点D到MN的距离h1(米)与D到OO′的距离a(米)之间满足关系式h1=a2;右侧曲线BO上任一点F到MN的距离h2(米)与F到OO′的距离b(米)之间满足关系式h2=﹣b3+6b.已知点B到OO′的距离为40米.
(1)求桥AB的长度;
(2)计划在谷底两侧建造平行于OO′的桥墩CD和EF,且CE为80米,其中C,E在AB上(不包括端点).桥墩EF每米造价k(万元),桥墩CD每米造价k(万元)(k>0),问O′E为多少米时,桥墩CD与EF的总造价最低?
【分析】(1)由题意可令b=40,求得h2,即O'O的长,再令h1=|OO'|,求得a,可得|AB|=a+b;
(2)可设O′E=x,则CO'=80﹣x,0<x<40,求得总造价y=k[160﹣(80﹣x)2]+k[160﹣(6x﹣x3)],化简整理,应用导数,求得单调区间,可得最小值.
解:(1)h2=﹣b3+6b,
点B到OO′的距离为40米,可令b=40,
可得h2=﹣×403+6×40=160,
即为|O'O|=160,由题意可设h1=160,
由a2=160,解得a=80,
则|AB|=80+40=120米;
(2)可设O′E=x,则CO'=80﹣x,由,可得0<x<40,
总造价为y=k[160﹣(80﹣x)2]+k[160﹣(6x﹣x3)]
=(x3﹣30x2+160×800),
y′=(3x2﹣60x)=x(x﹣20),由k>0,当0<x<20时,y′<0,函数y递减;
当20<x<40时,y′>0,函数y递增,所以当x=20时,y取得最小值,即总造价最低.
答:(1)桥|AB|长为120米;(2)O′E为20米时,桥墩CD与EF的总造价最低.
18.(16分)在平面直角坐标系xOy中,已知椭圆E:=1的左、右焦点分别为F1、F2,点A在椭圆E上且在第一象限内,AF2⊥F1F2,直线AF1与椭圆E相交于另一点B.
(1)求△AF1F2的周长;
(2)在x轴上任取一点P,直线AP与椭圆E的右准线相交于点Q,求的最小值;
(3)设点M在椭圆E上,记△OAB与△MAB的面积分别为S1,S2,若S2=3S1,求点M的坐标.
【分析】(1)由椭圆标准方程可知a,b,c的值,根据椭圆的定义可得△AF1F2的周长=2a+2c,代入计算即可.
(2)由椭圆方程得A(1,),设P(t,0),进而由点斜式写出直线AP方程,再结合椭圆的右准线为:x=4,得点Q为(4,?),再由向量数量积计算最小值即可.
(3)在计算△OAB与△MAB的面积时,AB可以最为同底,所以若S2=3S1,则O到直线AB距离d1与M到直线AB距离d2,之间的关系为d2=3d1,根据点到直线距离公式可得d1=,d2=,所以题意可以转化为M点应为与直线AB平行且距离为的直线与椭圆的交点,设平行于AB的直线l为3x﹣4y+m=0,与直线AB的距离为,根据两平行直线距离公式可得,m=﹣6或12,然后在分两种情况算出M点的坐标即可.
解:(1)由椭圆的标准方程可知,a2=4,b2=3,c2=a2﹣b2=1,
所以△AF1F2的周长=2a+2c=6.
(2)由椭圆方程得A(1,),设P(t,0),则直线AP方程为y=,
椭圆的右准线为:x==4,
所以直线AP与右准线的交点为Q(4,?),
?=(t,0)?(t﹣4,0﹣?)=t2﹣4t=(t﹣2)2﹣4≥﹣4,
当t=2时,()min=﹣4.
(3)若S2=3S1,设O到直线AB距离d1,M到直线AB距离d2,则×|AB|×d2=×|AB|×d1,即d2=3d1,
A(1,),F1(﹣1,0),可得直线AB方程为y=(x+1),即3x﹣4y+3=0,所以d1=,d2=,
由题意得,M点应为与直线AB平行且距离为的直线与椭圆的交点,
设平行于AB的直线l为3x﹣4y+m=0,与直线AB的距离为,
所以=,即m=﹣6或12,
当m=﹣6时,直线l为3x﹣4y﹣6=0,即y=(x﹣2),
联立,可得(x﹣2)(7x+2)=0,即或,
所以M(2,0)或(﹣,﹣).
当m=12时,直线l为3x﹣4y+12=0,即y=(x+4),
联立,可得+18x+24=0,△=9×(36﹣56)<0,所以无解,
综上所述,M点坐标为(2,0)或(﹣,﹣).
19.(16分)已知关于x的函数y=f(x),y=g(x)与h(x)=kx+b(k,b∈R)在区间D上恒有f(x)≥h(x)≥g(x).
(1)若f(x)=x2+2x,g(x)=﹣x2+2x,D=(﹣∞,+∞),求h(x)的表达式;
(2)若f(x)=x2﹣x+1,g(x)=klnx,h(x)=kx﹣k,D=(0,+∞),求k的取值范围;
(3)若f(x)=x4﹣2x2,g(x)=4x2﹣8,h(x)=4(t3﹣t)x﹣3t4+2t2(0<|t|≤),D=[m,n]?[﹣],求证:n﹣m≤.
【分析】(1)由f(x)=g(x)得x=0,求导可得f′(0)=g′(0)=2,能推出函数h(x)的图象为过原点,斜率为2的直线,进而可得h(x)=2x,再进行检验即可.
(2)由题可知h(x)﹣g(x)=k(x﹣1﹣lnx),设φ(x)=x﹣1﹣lnx,求导分析单调性可得,φ(x)≥φ(1)=0,那么要使的h(x)﹣g(x)≥0,则k≥0;令p(x)=f(x)﹣h(x)为二次函数,则要使得p(x)≥0,分两种情况,当x=k+1≤0时,当k+1>0时进行讨论,进而得出答案.
(3)因为f(x)=x4﹣2x2,求导,分析f(x)单调性及图象得函数y=f(x)的图象在x=x0处的切线为:y=(4x03﹣4x0)x﹣3x04+2x02,可推出直线y=h(x)为函数y=f(x)的图象在x=t(0<|t|≤)处的切线.进而f(x)≥h(x)在区间D上恒成立;在分析g(x)﹣h(x)=0,设4x2﹣4(t3﹣t)x+3t4﹣2t2﹣8=0,两根为x1,x2,由韦达定理可得x1+x2,x1x2,所以n﹣m=|x1﹣x2|=,再求最值即可得出结论.
解:(1)由f(x)=g(x)得x=0,
又f′(x)=2x+2,g′(x)=﹣2x+2,所以f′(0)=g′(0)=2,
所以,函数h(x)的图象为过原点,斜率为2的直线,所以h(x)=2x,
经检验:h(x)=2x,符合任意,
(2)h(x)﹣g(x)=k(x﹣1﹣lnx),
设φ(x)=x﹣1﹣lnx,设φ′(x)=1﹣=,
在(1,+∞)上,φ′(x)>0,φ(x)单调递增,
在(0,1)上,φ′(x)<0,φ(x)单调递减,
所以φ(x)≥φ(1)=0,
所以当h(x)﹣g(x)≥0时,k≥0,
令p(x)=f(x)﹣h(x)
所以p(x)=x2﹣x+1﹣(kx﹣k)=x2﹣(k+1)x+(1+k)≥0,得,
当x=k+1≤0时,即k≤﹣1时,f(x)在(0,+∞)上单调递增,
所以p(x)>p(0)=1+k≥0,k≥﹣1,
所以k=﹣1,
当k+1>0时,即k>﹣1时,
△≤0,即(k+1)2﹣4(k+1)≤0,
解得﹣1<k≤3,
综上,k∈[0,3].
(3)因为f(x)=x4﹣2x2,所以f′(x)=4x3﹣4x=4x(x+1)(x﹣1),
x
﹣
(﹣,﹣1)
﹣1
(﹣1,0)
0
(0,1)
1
(1,)
f′(x)
﹣
0
+
0
﹣
0
+
f(x)
0
↓
﹣1
↑
0
↓
﹣1
↑
0
所以函数y=f(x)的图象在x=x0处的切线为:
y=(4x03﹣4x0)(x﹣x0)+(x04﹣2x03)=(4x03﹣4x0)x﹣3x04+2x02,
可见直线y=h(x)为函数y=f(x)的图象在x=t(0<|t|≤)处的切线.
由函数y=f(x)的图象可知,当f(x)≥h(x)在区间D上恒成立时,|t|∈[1,],
又由g(x)﹣h(x)=0,得4x2﹣4(t3﹣t)x+3t4﹣2t2﹣8=0,
设方程g(x)﹣h(x)=0的两根为x1,x2,则x1+x2=t3﹣t,x1x2=,
所以|x1﹣x2|===,
t2=λ,则λ∈[1,2],由图象可知,n﹣m=|x1﹣x2|=,
设φ(λ)=λ3﹣5λ2+3λ+8,则φ′(λ)=3λ2﹣10λ+3=(λ﹣3)(3λ﹣1),
所以当λ∈[1,2]时,φ′(λ)<0,φ(λ)单调递减,
所以φ(λ)max=φ(1)=7,
故(n﹣m)max=|x1﹣x2|max=,即n﹣m≤.
20.(16分)已知数列{an}(n∈N
)的首项a1=1,前n项和为Sn.设λ和k为常数,若对一切正整数n,均有Sn+1﹣Sn=λan+1成立,则称此数列为“λ﹣k”数列.
(1)若等差数列{an}是“λ﹣1”数列,求λ的值;
(2)若数列{an}是“﹣2”数列,且an>0,求数列{an}的通项公式;
(3)对于给定的λ,是否存在三个不同的数列{an}为“λ﹣3”数列,且an≥0?若存在,求出λ的取值范围;若不存在,说明理由.
【分析】(1)由“λ﹣1”数列可得k=1,结合数列的递推式,以及等差数列的定义,可得λ的值;
(2)运用“﹣2”数列的定义,结合数列的递推式和等比数列的通项公式,可得所求通项公式;
(3)若存在三个不同的数列{an}为“λ﹣3”数列,则Sn+1﹣Sn=λan+1,由两边立方,结合数列的递推式,以及t的讨论,二次方程的实根分布和韦达定理,即可判断是否存在λ,并可得取值范围.
解:(1)k=1时,an+1=Sn+1﹣Sn=λan+1,由n为任意正整数,且a1=1,an≠0,可得λ=1;
(2)﹣=,则an+1=Sn+1﹣Sn=(﹣)?(+)=?(+),
因此+=?,即=,Sn+1=an+1=(Sn+1﹣Sn),
从而Sn+1=4Sn,又S1=a1=1,可得Sn=4n﹣1,
an=Sn﹣Sn﹣1=3?4n﹣2,n≥2,
综上可得an=,n∈N
;
(3)若存在三个不同的数列{an}为“λ﹣3”数列,
则Sn+1﹣Sn=λan+1,
则Sn+1﹣3Sn+1Sn+3Sn+1Sn﹣Sn=λ3an+1=λ3(Sn+1﹣Sn),
由a1=1,an≥0,且Sn>0,令pn=()>0,
则(1﹣λ3)pn3﹣3pn2+3pn﹣(1﹣λ3)=0,
λ=1时,pn=pn2,
由pn>0,可得pn=1,则Sn+1=Sn,
即an+1=0,
此时{an}唯一,不存在三个不同的数列{an},
λ≠1时,令t=,则pn3﹣tpn2+tpn﹣1=0,则(pn﹣1)[pn2+(1﹣t)pn+1]=0,
①t≤1时,pn2+(1﹣t)pn+1>0,则pn=1,同上分析不存在三个不同的数列{an};
②1<t<3时,△=(1﹣t)2﹣4<0,pn2+(1﹣t)pn+1=0无解,
则pn=1,同上分析不存在三个不同的数列{an};
③t=3时,(pn﹣1)3=0,则pn=1,同上分析不存在三个不同的数列{an}.
④t>3时,即0<λ<1时,△=(1﹣t)2﹣4>0,pn2+(1﹣t)pn+1=0有两解α,β,
设α<β,α+β=t﹣1>2,αβ=1>0,则0<α<1<β,
则对任意n∈N
,=1或=α3或=β3,此时Sn=1,Sn=,Sn=均符合条件.
对应an=,an=,an=,
则存在三个不同的数列{an}为“λ﹣3”数列,且an≥0,
综上可得0<λ<1.
一、选择题
21.系统找不到该试题
B.[选修4-4:坐标系与参数方程](本小题满分10分)
22.系统找不到该试题
C.[选修4-5:不等式选讲](本小题满分0分)
23.系统找不到该试题
【必做题】第24题、第25题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
24.系统找不到该试题
25.系统找不到该试题
一、填空题(共14小题).
1.已知集合A={﹣1,0,1,2},B={0,2,3},则A∩B=
.
2.已知i是虚数单位,则复数z=(1+i)(2﹣i)的实部是
.
3.已知一组数据4,2a,3﹣a,5,6的平均数为4,则a的值是
.
4.将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是
.
5.如图是一个算法流程图,若输出y的值为﹣2,则输入x的值是
.
6.在平面直角坐标系xOy中,若双曲线﹣=1(a>0)的一条渐近线方程为y=x,则该双曲线的离心率是
.
7.已知y=f(x)是奇函数,当x≥0时,f(x)=x,则f(﹣8)的值是
.
8.已知sin2(+α)=,则sin2α的值是
.
9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2cm,高为2cm,内孔半径为0.5cm,则此六角螺帽毛坯的体积是
cm3.
10.将函数y=3sin(2x+)的图象向右平移个单位长度,则平移后的图象中与y轴最近的对称轴的方程是
.
11.设{an}是公差为d的等差数列,{bn}是公比为q的等比数列.已知数列{an+bn}的前n项和Sn=n2﹣n+2n﹣1(n∈N
),则d+q的值是
.
12.已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值是
.
13.在△ABC中,AB=4,AC=3,∠BAC=90°,D在边BC上,延长AD到P,使得AP=9.若=m+(﹣m)(m为常数),则CD的长度是
.
14.在平面直角坐标系xOy中,已知P(,0),A、B是圆C:x2+(y﹣)2=36上的两个动点,满足PA=PB,则△PAB面积的最大值是
.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.在三棱柱ABC﹣A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.
(1)求证:EF∥平面AB1C1;
(2)求证:平面AB1C⊥平面ABB1.
16.在△ABC中,角A、B、C的对边分别为a、b、c.已知a=3,c=,B=45°.
(1)求sinC的值;
(2)在边BC上取一点D,使得cos∠ADC=﹣,求tan∠DAC的值.
17.某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O在水平线MN上,桥AB与MN平行,OO′为铅垂线(O′在AB上).经测量,左侧曲线AO上任一点D到MN的距离h1(米)与D到OO′的距离a(米)之间满足关系式h1=a2;右侧曲线BO上任一点F到MN的距离h2(米)与F到OO′的距离b(米)之间满足关系式h2=﹣b3+6b.已知点B到OO′的距离为40米.
(1)求桥AB的长度;
(2)计划在谷底两侧建造平行于OO′的桥墩CD和EF,且CE为80米,其中C,E在AB上(不包括端点).桥墩EF每米造价k(万元),桥墩CD每米造价k(万元)(k>0),问O′E为多少米时,桥墩CD与EF的总造价最低?
18.(16分)在平面直角坐标系xOy中,已知椭圆E:=1的左、右焦点分别为F1、F2,点A在椭圆E上且在第一象限内,AF2⊥F1F2,直线AF1与椭圆E相交于另一点B.
(1)求△AF1F2的周长;
(2)在x轴上任取一点P,直线AP与椭圆E的右准线相交于点Q,求的最小值;
(3)设点M在椭圆E上,记△OAB与△MAB的面积分别为S1,S2,若S2=3S1,求点M的坐标.
19.(16分)已知关于x的函数y=f(x),y=g(x)与h(x)=kx+b(k,b∈R)在区间D上恒有f(x)≥h(x)≥g(x).
(1)若f(x)=x2+2x,g(x)=﹣x2+2x,D=(﹣∞,+∞),求h(x)的表达式;
(2)若f(x)=x2﹣x+1,g(x)=klnx,h(x)=kx﹣k,D=(0,+∞),求k的取值范围;
(3)若f(x)=x4﹣2x2,g(x)=4x2﹣8,h(x)=4(t3﹣t)x﹣3t4+2t2(0<|t|≤),D=[m,n]?[﹣],求证:n﹣m≤.
20.(16分)已知数列{an}(n∈N
)的首项a1=1,前n项和为Sn.设λ和k为常数,若对一切正整数n,均有Sn+1﹣Sn=λan+1成立,则称此数列为“λ﹣k”数列.
(1)若等差数列{an}是“λ﹣1”数列,求λ的值;
(2)若数列{an}是“﹣2”数列,且an>0,求数列{an}的通项公式;
(3)对于给定的λ,是否存在三个不同的数列{an}为“λ﹣3”数列,且an≥0?若存在,求出λ的取值范围;若不存在,说明理由.
【选做题】本题包括A、B、C三小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-2:矩阵与变换](本小题满分10分)
21.系统找不到该试题
B.[选修4-4:坐标系与参数方程](本小题满分10分)
22.系统找不到该试题
C.[选修4-5:不等式选讲](本小题满分0分)
23.系统找不到该试题
【必做题】第24题、第25题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
24.系统找不到该试题
25.系统找不到该试题
参考答案
一、填空题:本题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上.
1.已知集合A={﹣1,0,1,2},B={0,2,3},则A∩B= {0,2} .
【分析】运用集合的交集运算,可得所求集合.
解:集合B={0,2,3},A={﹣1,0,1,2},
则A∩B={0,2},
故答案为:{0,2}.
2.已知i是虚数单位,则复数z=(1+i)(2﹣i)的实部是 3 .
【分析】利用复数的乘法的运算法则,化简求解即可.
解:复数z=(1+i)(2﹣i)=3+i,
所以复数z=(1+i)(2﹣i)的实部是:3.
故答案为:3.
3.已知一组数据4,2a,3﹣a,5,6的平均数为4,则a的值是 2 .
【分析】运用平均数的定义,解方程可得a的值.
解:一组数据4,2a,3﹣a,5,6的平均数为4,
则4+2a+(3﹣a)+5+6=4×5,
解得a=2.
故答案为:2.
4.将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是 .
【分析】分别求得基本事件的总数和点数和为5的事件数,由古典概率的计算公式可得所求值.
解:一颗质地均匀的正方体骰子先后抛掷2次,可得基本事件的总数为6×6=36种,
而点数和为5的事件为(1,4),(2,3),(3,2),(4,1),共4种,
则点数和为5的概率为P==.
故答案为:.
5.如图是一个算法流程图,若输出y的值为﹣2,则输入x的值是 ﹣3 .
【分析】由已知中的程序语句可知:该程序的功能是利用程序框图表达式为分段函数计算并输出变量y的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解:由题意可得程序框图表达式为分段函数y=,
若输出y值为﹣2时,由于2x>0,
所以解x+1=﹣2,
即x=﹣3,
故答案为:﹣3,
6.在平面直角坐标系xOy中,若双曲线﹣=1(a>0)的一条渐近线方程为y=x,则该双曲线的离心率是 .
【分析】利用双曲线的渐近线方程,求出a,然后求解双曲线的离心率即可.
解:双曲线﹣=1(a>0)的一条渐近线方程为y=x,可得,所以a=2,
所以双曲线的离心率为:e==,
故答案为:.
7.已知y=f(x)是奇函数,当x≥0时,f(x)=x,则f(﹣8)的值是 ﹣4 .
【分析】由奇函数的定义可得f(﹣x)=﹣f(x),由已知可得f(8),进而得到f(﹣8).
解:y=f(x)是奇函数,可得f(﹣x)=﹣f(x),
当x≥0时,f(x)=x,可得f(8)=8=4,
则f(﹣8)=﹣f(8)=﹣4,
故答案为:﹣4.
8.已知sin2(+α)=,则sin2α的值是 .
【分析】根据二倍角公式即可求出.
解:因为sin2(+α)=,则sin2(+α)===,
解得sin2α=,
故答案为:
9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2cm,高为2cm,内孔半径为0.5cm,则此六角螺帽毛坯的体积是 12 cm3.
【分析】通过棱柱的体积减去圆柱的体积,即可推出结果.
解:六棱柱的体积为:,
圆柱的体积为:π×(0.5)2×2=,
所以此六角螺帽毛坯的体积是:(12)cm3,
故答案为:12.
10.将函数y=3sin(2x+)的图象向右平移个单位长度,则平移后的图象中与y轴最近的对称轴的方程是 x=﹣ .
【分析】利用三角函数的平移可得新函数g(x)=f(x﹣),求g(x)的所有对称轴x=+,k∈Z,从而可判断平移后的图象中与y轴最近的对称轴的方程,
解:因为函数y=3sin(2x+)的图象向右平移个单位长度可得
g(x)=f(x﹣)=3sin(2x﹣+)=3sin(2x﹣),
则y=g(x)的对称轴为2x﹣=+kπ,k∈Z,
即x=+,k∈Z,
当k=0时,x=,
当k=﹣1时,x=,
所以平移后的图象中与y轴最近的对称轴的方程是x=,
故答案为:x=,
11.设{an}是公差为d的等差数列,{bn}是公比为q的等比数列.已知数列{an+bn}的前n项和Sn=n2﹣n+2n﹣1(n∈N
),则d+q的值是 4 .
【分析】由{an+bn}的前n项和Sn=n2﹣n+2n﹣1(n∈N
),由{an}是公差为d的等差数列,设首项为a1;求出等差数列的前n项和的表达式;{bn}是公比为q的等比数列,设首项为b1,讨论当q为1和不为1时的前n项和的表达式,由题意可得q≠1,由对应项的系数相等可得d,q的值,进而求出d+q的值.
解:因为{an+bn}的前n项和Sn=n2﹣n+2n﹣1(n∈N
),
因为{an}是公差为d的等差数列,设首项为a1;{bn}是公比为q的等比数列,设首项为b1,
所以{an}的通项公式an=a1+(n﹣1)d,所以其前n项和S==n2+(a1﹣)n,
当{bn}中,当公比q=1时,其前n项和S=nb1,
所以{an+bn}的前n项和Sn=S+S=n2+(a1﹣)n+nb1=n2﹣n+2n﹣1(n∈N
),显然没有出现2n,所以q≠1,
则{bn}的前n项和为S==+,
所以Sn=S+S=n2+(a1﹣)n+﹣=n2﹣n+2n﹣1(n∈N
),
由两边对应项相等可得:解得:d=2,a1=0,q=2,b1=1,
所以d+q=4,
故答案为:4.
12.已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值是 .
【分析】方法一、由已知求得x2,代入所求式子,整理后,运用基本不等式可得所求最小值;
方法二、由4=(5x2+y2)?4y2,运用基本不等式,计算可得所求最小值.
解:方法一、由5x2y2+y4=1,可得x2=,
由x2≥0,可得y2∈(0,1],
则x2+y2=+y2==(4y2+)
≥?2=,当且仅当y2=,x2=,
可得x2+y2的最小值为;
方法二、4=(5x2+y2)?4y2≤()2=(x2+y2)2,
故x2+y2≥,
当且仅当5x2+y2=4y2=2,即y2=,x2=时取得等号,
可得x2+y2的最小值为.
故答案为:.
13.在△ABC中,AB=4,AC=3,∠BAC=90°,D在边BC上,延长AD到P,使得AP=9.若=m+(﹣m)(m为常数),则CD的长度是 0或 .
【分析】以A为坐标原点,分别以AB,AC所在直线为x,y轴建立平面直角坐标系,求得B与C的坐标,再把的坐标用m表示.由AP=9列式求得m值,然后分类求得D的坐标,则CD的长度可求.
解:如图,以A为坐标原点,分别以AB,AC所在直线为x,y轴建立平面直角坐标系,
则B(4,0),C(0,3),
由=m+(﹣m),得,
整理得:
=﹣2m(4,0)+(2m﹣3)(0,3)=(﹣8m,6m﹣9).
由AP=9,得64m2+(6m﹣9)2=81,解得m=或m=0.
当m=0时,,此时C与D重合,|CD|=0;
当m=时,直线PA的方程为y=x,
直线BC的方程为,
联立两直线方程可得x=m,y=3﹣2m.
即D(,),
∴|CD|=.
∴CD的长度是0或.
故答案为:0或.
14.在平面直角坐标系xOy中,已知P(,0),A、B是圆C:x2+(y﹣)2=36上的两个动点,满足PA=PB,则△PAB面积的最大值是 10 .
【分析】求得圆的圆心C和半径,作PC所在直径EF,交AB于点D,运用垂径定理和勾股定理,以及三角形的面积公式,由三角换元,结合函数的导数,求得单调区间,计算可得所求最大值.
解:圆C:x2+(y﹣)2=36的圆心C(0,),半径为6,
如图,作PC所在直径EF,交AB于点D,
因为PA=PB,CA=CB=R=6,所以PC⊥AB,EF为垂径,
要使面积S△PAB最大,则P,D位于C的两侧,
并设CD=x,可得PC==1,故PD=1+x,AB=2BD=2,
可令x=6cosθ,
S△PAB=|AB|?|PD|=(1+x)=(1+6cosθ)?6sinθ=6sinθ+18sin2θ,0<θ≤,
设函数f(θ)=6sinθ+18sin2θ,0<θ≤,
f′(θ)=6cosθ+36cos2θ=6(12cos2θ+cosθ﹣6),
由f′(θ)=6(12cos2θ+cosθ﹣6)=0,解得cosθ=(cosθ=﹣<0舍去),
显然,当0≤cosθ<,f′(θ)<0,f(θ)递减;当<cosθ<1时,f′(θ)>0,f(θ)递增,
结合cosθ在(0,)递减,故cosθ=时,f(θ)最大,此时sinθ==,
故f(θ)max=6×+36××=10,
则△PAB面积的最大值为10.
故答案为:10.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.在三棱柱ABC﹣A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.
(1)求证:EF∥平面AB1C1;
(2)求证:平面AB1C⊥平面ABB1.
【分析】(1)证明EF∥AB1,然后利用直线与平面平行的判断定理证明EF∥平面AB1C1;
(2)证明B1C⊥AB,结合AB⊥AC,证明AB⊥平面AB1C,然后证明平面AB1C⊥平面ABB1.
【解答】证明:(1)E,F分别是AC,B1C的中点.
所以EF∥AB1,因为EF?平面AB1C1,AB1?平面AB1C1,
所以EF∥平面AB1C1;
(2)因为B1C⊥平面ABC,AB?平面ABB1,
所以B1C⊥AB,
又因为AB⊥AC,AC∩B1C=C,AC?平面AB1C,B1C?平面AB1C,
所以AB⊥平面AB1C,
因为AB?平面ABB1,
所以平面AB1C⊥平面ABB1.
16.在△ABC中,角A、B、C的对边分别为a、b、c.已知a=3,c=,B=45°.
(1)求sinC的值;
(2)在边BC上取一点D,使得cos∠ADC=﹣,求tan∠DAC的值.
【分析】(1)由题意及余弦定理求出b边,再由正弦定理求出sinC的值;
(2)三角形的内角和为180°,cos∠ADC=﹣,可得∠ADC为钝角,可得∠DAC与∠ADC+∠C互为补角,所以sin∠DAC=sin(∠ADC+∠C)展开可得sin∠DAC及cos∠DAC,进而求出tan∠DAC的值.
解:(1)因为a=3,c=,B=45°.,由余弦定理可得:b===,
由正弦定理可得=,所以sinC=?sin45°==,
所以sinC=;
(2)因为cos∠ADC=﹣,所以sin∠ADC==,
在三角形ADC
中,易知C为锐角,由(1)可得cosC==,
所以在三角形ADC中,sin∠DAC=sin(∠ADC+∠C)=sin∠ADCcos∠C+cos∠ADCsin∠C=,
因为∠DAC,所以cos∠DAC==,
所以tan∠DAC==.
17.某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O在水平线MN上,桥AB与MN平行,OO′为铅垂线(O′在AB上).经测量,左侧曲线AO上任一点D到MN的距离h1(米)与D到OO′的距离a(米)之间满足关系式h1=a2;右侧曲线BO上任一点F到MN的距离h2(米)与F到OO′的距离b(米)之间满足关系式h2=﹣b3+6b.已知点B到OO′的距离为40米.
(1)求桥AB的长度;
(2)计划在谷底两侧建造平行于OO′的桥墩CD和EF,且CE为80米,其中C,E在AB上(不包括端点).桥墩EF每米造价k(万元),桥墩CD每米造价k(万元)(k>0),问O′E为多少米时,桥墩CD与EF的总造价最低?
【分析】(1)由题意可令b=40,求得h2,即O'O的长,再令h1=|OO'|,求得a,可得|AB|=a+b;
(2)可设O′E=x,则CO'=80﹣x,0<x<40,求得总造价y=k[160﹣(80﹣x)2]+k[160﹣(6x﹣x3)],化简整理,应用导数,求得单调区间,可得最小值.
解:(1)h2=﹣b3+6b,
点B到OO′的距离为40米,可令b=40,
可得h2=﹣×403+6×40=160,
即为|O'O|=160,由题意可设h1=160,
由a2=160,解得a=80,
则|AB|=80+40=120米;
(2)可设O′E=x,则CO'=80﹣x,由,可得0<x<40,
总造价为y=k[160﹣(80﹣x)2]+k[160﹣(6x﹣x3)]
=(x3﹣30x2+160×800),
y′=(3x2﹣60x)=x(x﹣20),由k>0,当0<x<20时,y′<0,函数y递减;
当20<x<40时,y′>0,函数y递增,所以当x=20时,y取得最小值,即总造价最低.
答:(1)桥|AB|长为120米;(2)O′E为20米时,桥墩CD与EF的总造价最低.
18.(16分)在平面直角坐标系xOy中,已知椭圆E:=1的左、右焦点分别为F1、F2,点A在椭圆E上且在第一象限内,AF2⊥F1F2,直线AF1与椭圆E相交于另一点B.
(1)求△AF1F2的周长;
(2)在x轴上任取一点P,直线AP与椭圆E的右准线相交于点Q,求的最小值;
(3)设点M在椭圆E上,记△OAB与△MAB的面积分别为S1,S2,若S2=3S1,求点M的坐标.
【分析】(1)由椭圆标准方程可知a,b,c的值,根据椭圆的定义可得△AF1F2的周长=2a+2c,代入计算即可.
(2)由椭圆方程得A(1,),设P(t,0),进而由点斜式写出直线AP方程,再结合椭圆的右准线为:x=4,得点Q为(4,?),再由向量数量积计算最小值即可.
(3)在计算△OAB与△MAB的面积时,AB可以最为同底,所以若S2=3S1,则O到直线AB距离d1与M到直线AB距离d2,之间的关系为d2=3d1,根据点到直线距离公式可得d1=,d2=,所以题意可以转化为M点应为与直线AB平行且距离为的直线与椭圆的交点,设平行于AB的直线l为3x﹣4y+m=0,与直线AB的距离为,根据两平行直线距离公式可得,m=﹣6或12,然后在分两种情况算出M点的坐标即可.
解:(1)由椭圆的标准方程可知,a2=4,b2=3,c2=a2﹣b2=1,
所以△AF1F2的周长=2a+2c=6.
(2)由椭圆方程得A(1,),设P(t,0),则直线AP方程为y=,
椭圆的右准线为:x==4,
所以直线AP与右准线的交点为Q(4,?),
?=(t,0)?(t﹣4,0﹣?)=t2﹣4t=(t﹣2)2﹣4≥﹣4,
当t=2时,()min=﹣4.
(3)若S2=3S1,设O到直线AB距离d1,M到直线AB距离d2,则×|AB|×d2=×|AB|×d1,即d2=3d1,
A(1,),F1(﹣1,0),可得直线AB方程为y=(x+1),即3x﹣4y+3=0,所以d1=,d2=,
由题意得,M点应为与直线AB平行且距离为的直线与椭圆的交点,
设平行于AB的直线l为3x﹣4y+m=0,与直线AB的距离为,
所以=,即m=﹣6或12,
当m=﹣6时,直线l为3x﹣4y﹣6=0,即y=(x﹣2),
联立,可得(x﹣2)(7x+2)=0,即或,
所以M(2,0)或(﹣,﹣).
当m=12时,直线l为3x﹣4y+12=0,即y=(x+4),
联立,可得+18x+24=0,△=9×(36﹣56)<0,所以无解,
综上所述,M点坐标为(2,0)或(﹣,﹣).
19.(16分)已知关于x的函数y=f(x),y=g(x)与h(x)=kx+b(k,b∈R)在区间D上恒有f(x)≥h(x)≥g(x).
(1)若f(x)=x2+2x,g(x)=﹣x2+2x,D=(﹣∞,+∞),求h(x)的表达式;
(2)若f(x)=x2﹣x+1,g(x)=klnx,h(x)=kx﹣k,D=(0,+∞),求k的取值范围;
(3)若f(x)=x4﹣2x2,g(x)=4x2﹣8,h(x)=4(t3﹣t)x﹣3t4+2t2(0<|t|≤),D=[m,n]?[﹣],求证:n﹣m≤.
【分析】(1)由f(x)=g(x)得x=0,求导可得f′(0)=g′(0)=2,能推出函数h(x)的图象为过原点,斜率为2的直线,进而可得h(x)=2x,再进行检验即可.
(2)由题可知h(x)﹣g(x)=k(x﹣1﹣lnx),设φ(x)=x﹣1﹣lnx,求导分析单调性可得,φ(x)≥φ(1)=0,那么要使的h(x)﹣g(x)≥0,则k≥0;令p(x)=f(x)﹣h(x)为二次函数,则要使得p(x)≥0,分两种情况,当x=k+1≤0时,当k+1>0时进行讨论,进而得出答案.
(3)因为f(x)=x4﹣2x2,求导,分析f(x)单调性及图象得函数y=f(x)的图象在x=x0处的切线为:y=(4x03﹣4x0)x﹣3x04+2x02,可推出直线y=h(x)为函数y=f(x)的图象在x=t(0<|t|≤)处的切线.进而f(x)≥h(x)在区间D上恒成立;在分析g(x)﹣h(x)=0,设4x2﹣4(t3﹣t)x+3t4﹣2t2﹣8=0,两根为x1,x2,由韦达定理可得x1+x2,x1x2,所以n﹣m=|x1﹣x2|=,再求最值即可得出结论.
解:(1)由f(x)=g(x)得x=0,
又f′(x)=2x+2,g′(x)=﹣2x+2,所以f′(0)=g′(0)=2,
所以,函数h(x)的图象为过原点,斜率为2的直线,所以h(x)=2x,
经检验:h(x)=2x,符合任意,
(2)h(x)﹣g(x)=k(x﹣1﹣lnx),
设φ(x)=x﹣1﹣lnx,设φ′(x)=1﹣=,
在(1,+∞)上,φ′(x)>0,φ(x)单调递增,
在(0,1)上,φ′(x)<0,φ(x)单调递减,
所以φ(x)≥φ(1)=0,
所以当h(x)﹣g(x)≥0时,k≥0,
令p(x)=f(x)﹣h(x)
所以p(x)=x2﹣x+1﹣(kx﹣k)=x2﹣(k+1)x+(1+k)≥0,得,
当x=k+1≤0时,即k≤﹣1时,f(x)在(0,+∞)上单调递增,
所以p(x)>p(0)=1+k≥0,k≥﹣1,
所以k=﹣1,
当k+1>0时,即k>﹣1时,
△≤0,即(k+1)2﹣4(k+1)≤0,
解得﹣1<k≤3,
综上,k∈[0,3].
(3)因为f(x)=x4﹣2x2,所以f′(x)=4x3﹣4x=4x(x+1)(x﹣1),
x
﹣
(﹣,﹣1)
﹣1
(﹣1,0)
0
(0,1)
1
(1,)
f′(x)
﹣
0
+
0
﹣
0
+
f(x)
0
↓
﹣1
↑
0
↓
﹣1
↑
0
所以函数y=f(x)的图象在x=x0处的切线为:
y=(4x03﹣4x0)(x﹣x0)+(x04﹣2x03)=(4x03﹣4x0)x﹣3x04+2x02,
可见直线y=h(x)为函数y=f(x)的图象在x=t(0<|t|≤)处的切线.
由函数y=f(x)的图象可知,当f(x)≥h(x)在区间D上恒成立时,|t|∈[1,],
又由g(x)﹣h(x)=0,得4x2﹣4(t3﹣t)x+3t4﹣2t2﹣8=0,
设方程g(x)﹣h(x)=0的两根为x1,x2,则x1+x2=t3﹣t,x1x2=,
所以|x1﹣x2|===,
t2=λ,则λ∈[1,2],由图象可知,n﹣m=|x1﹣x2|=,
设φ(λ)=λ3﹣5λ2+3λ+8,则φ′(λ)=3λ2﹣10λ+3=(λ﹣3)(3λ﹣1),
所以当λ∈[1,2]时,φ′(λ)<0,φ(λ)单调递减,
所以φ(λ)max=φ(1)=7,
故(n﹣m)max=|x1﹣x2|max=,即n﹣m≤.
20.(16分)已知数列{an}(n∈N
)的首项a1=1,前n项和为Sn.设λ和k为常数,若对一切正整数n,均有Sn+1﹣Sn=λan+1成立,则称此数列为“λ﹣k”数列.
(1)若等差数列{an}是“λ﹣1”数列,求λ的值;
(2)若数列{an}是“﹣2”数列,且an>0,求数列{an}的通项公式;
(3)对于给定的λ,是否存在三个不同的数列{an}为“λ﹣3”数列,且an≥0?若存在,求出λ的取值范围;若不存在,说明理由.
【分析】(1)由“λ﹣1”数列可得k=1,结合数列的递推式,以及等差数列的定义,可得λ的值;
(2)运用“﹣2”数列的定义,结合数列的递推式和等比数列的通项公式,可得所求通项公式;
(3)若存在三个不同的数列{an}为“λ﹣3”数列,则Sn+1﹣Sn=λan+1,由两边立方,结合数列的递推式,以及t的讨论,二次方程的实根分布和韦达定理,即可判断是否存在λ,并可得取值范围.
解:(1)k=1时,an+1=Sn+1﹣Sn=λan+1,由n为任意正整数,且a1=1,an≠0,可得λ=1;
(2)﹣=,则an+1=Sn+1﹣Sn=(﹣)?(+)=?(+),
因此+=?,即=,Sn+1=an+1=(Sn+1﹣Sn),
从而Sn+1=4Sn,又S1=a1=1,可得Sn=4n﹣1,
an=Sn﹣Sn﹣1=3?4n﹣2,n≥2,
综上可得an=,n∈N
;
(3)若存在三个不同的数列{an}为“λ﹣3”数列,
则Sn+1﹣Sn=λan+1,
则Sn+1﹣3Sn+1Sn+3Sn+1Sn﹣Sn=λ3an+1=λ3(Sn+1﹣Sn),
由a1=1,an≥0,且Sn>0,令pn=()>0,
则(1﹣λ3)pn3﹣3pn2+3pn﹣(1﹣λ3)=0,
λ=1时,pn=pn2,
由pn>0,可得pn=1,则Sn+1=Sn,
即an+1=0,
此时{an}唯一,不存在三个不同的数列{an},
λ≠1时,令t=,则pn3﹣tpn2+tpn﹣1=0,则(pn﹣1)[pn2+(1﹣t)pn+1]=0,
①t≤1时,pn2+(1﹣t)pn+1>0,则pn=1,同上分析不存在三个不同的数列{an};
②1<t<3时,△=(1﹣t)2﹣4<0,pn2+(1﹣t)pn+1=0无解,
则pn=1,同上分析不存在三个不同的数列{an};
③t=3时,(pn﹣1)3=0,则pn=1,同上分析不存在三个不同的数列{an}.
④t>3时,即0<λ<1时,△=(1﹣t)2﹣4>0,pn2+(1﹣t)pn+1=0有两解α,β,
设α<β,α+β=t﹣1>2,αβ=1>0,则0<α<1<β,
则对任意n∈N
,=1或=α3或=β3,此时Sn=1,Sn=,Sn=均符合条件.
对应an=,an=,an=,
则存在三个不同的数列{an}为“λ﹣3”数列,且an≥0,
综上可得0<λ<1.
一、选择题
21.系统找不到该试题
B.[选修4-4:坐标系与参数方程](本小题满分10分)
22.系统找不到该试题
C.[选修4-5:不等式选讲](本小题满分0分)
23.系统找不到该试题
【必做题】第24题、第25题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
24.系统找不到该试题
25.系统找不到该试题
同课章节目录
