2020年高考全国卷Ⅰ(文科)数学试题(PDF版,含解析)
文档属性
| 名称 | 2020年高考全国卷Ⅰ(文科)数学试题(PDF版,含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 585.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-10 15:12:38 | ||
图片预览


文档简介
绝密★启用前
2020年普通高等学校招生全国统一考试
文科数学
注意事项
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑如需改动
用橡皮擦干净后,再选涂其他答案标号回答非选择题时,将答案写在答题卡上写在本试卷上
无效
3.考试结束后,将本试卷和答题卡并交回
选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有
项是符合题目要求的
1已知集合A={xx2-3x-4<0},B={41,3,5},则4∩B=()
A.{-4,1
B.{15
3S}
D.{13
【答案】D
【解析】
【分析】
首先解一元二次不等式求得集合A,之后利用交集中元素的特征求得4∩B,得到结果
【详解】由x2-3x-4<0解得-1所以A={x|-1又因为B={-435},所以A∩B={1,3},
故选:D
【点晴】该题考查的是有关集合的问题,涉及到的知识点有利用一元二次不等式的解法求集合,集合的交
运算,属于基础题目
2若z=1+2i+,则=()
A.0
D.2
【答案】C
【解析】
【分析】
先根据2=-1将=化简,再根据向量的模的计算公式即可求出
【详解】因为z=1+2+P=1+2-1=1+1,所以=2+12=
【点晴】本题主要考查向量的模的计算公式的应用,属于容易题
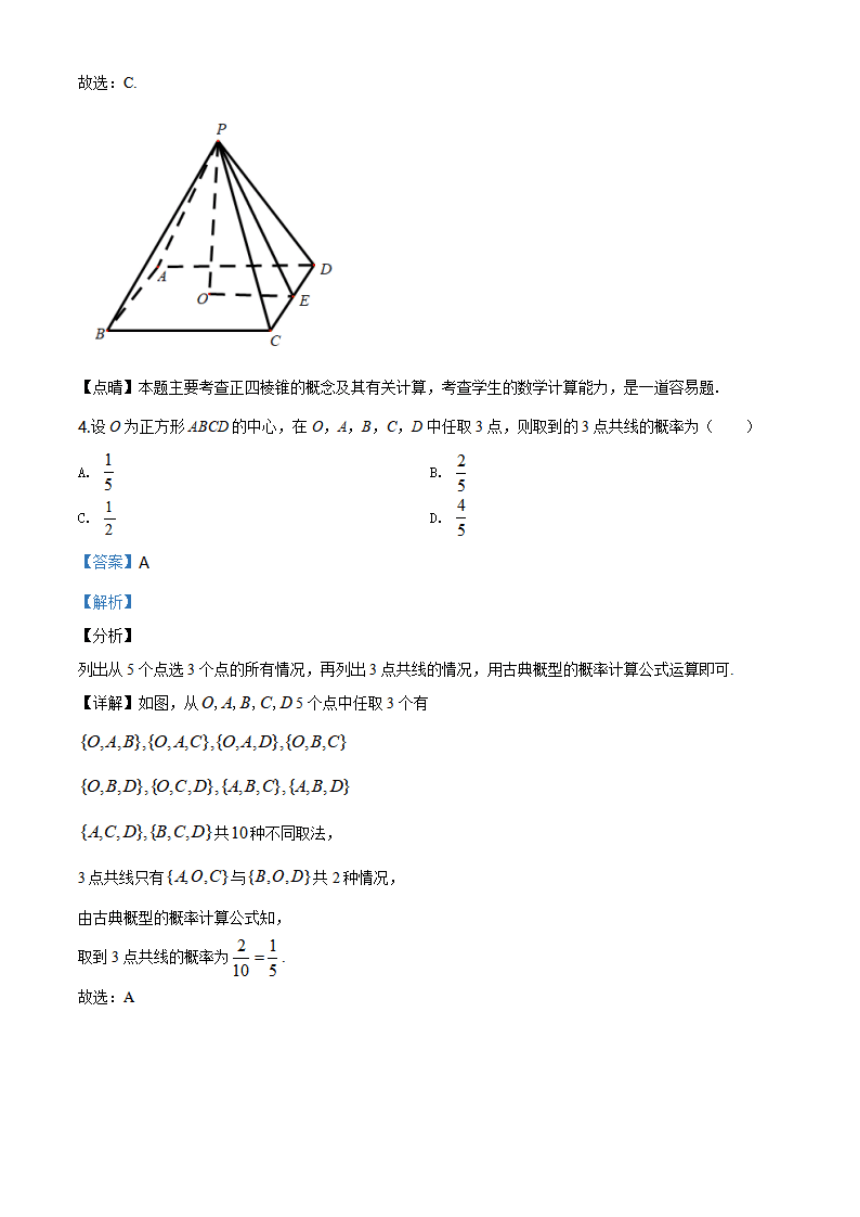
3埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方
形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为
()
√+1
【答案】D
【解析】
【分析】
设CD=aPE=b,利用PO2=CDPE得到关于a,b的方程,解方程即可得到笞案
【详解】如图,设CD=a,PE=b,则PO=√PE2-OE
由题意PO=2
b,即b
ab,化简得4(-)2-2--1=0
解得2=1+√5(负值含去)
故选:C
【点晴】本题主要考查正四棱锥的概念及其有关计算,考查学生的数学计算能力,是一道容易题
4设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为()
2-54-5
【答案】A
【解析】
【分析】
歹出从5个点选3个点的所有情况,再列出3点共线的情况,用古典概型的概率计算公式运算即可
【详解】如图,从O,A,B,C,D5个点中任取3个有
104,
B1,10,
A,
C.0
4,
D.O,
B,
C
to,
B,
D
0,
C,
D,
A,
B,
C
4,
B,
D
AC2D}2{BC2D}共10种不同取法,
3点共线只有{AOC}与{B,O,D共2种情冫
由古典概型的概率计算公式知,
取到3点共线的概率为2
5
故选:A
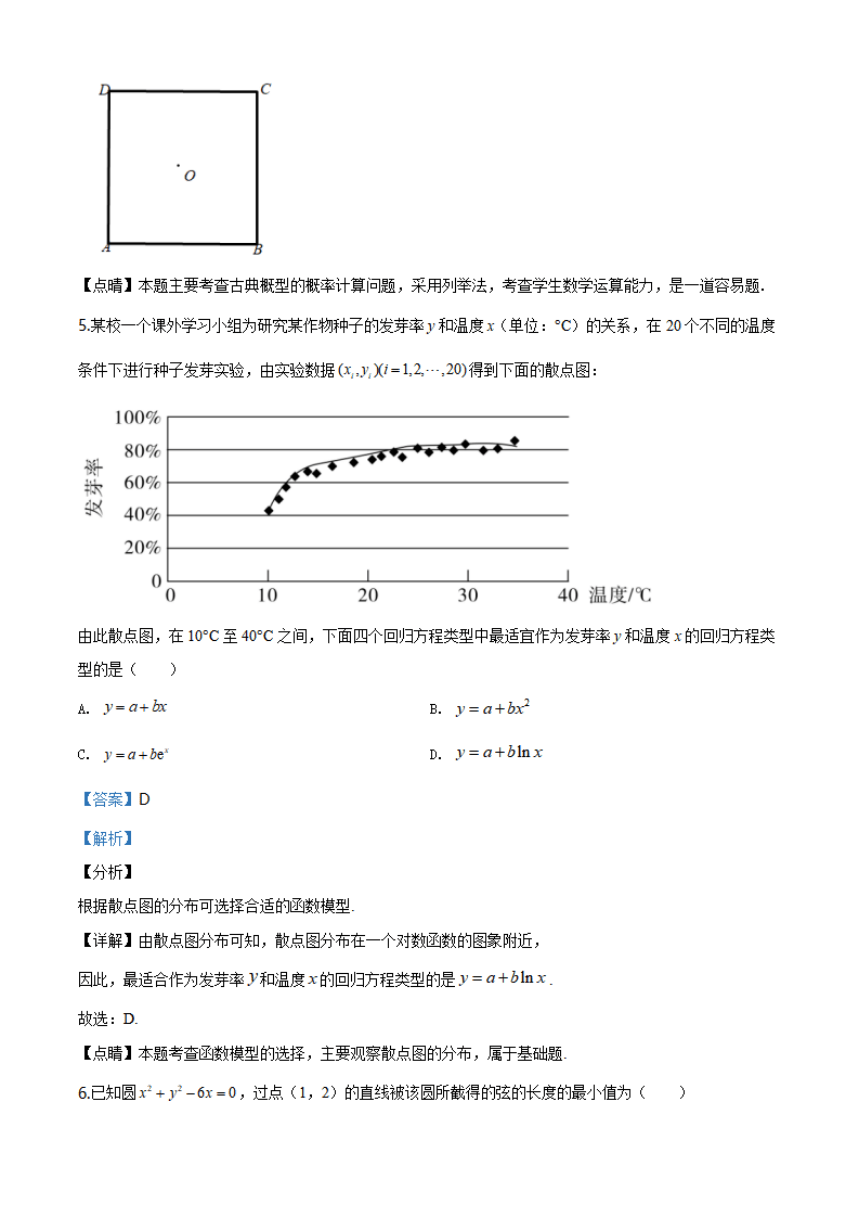
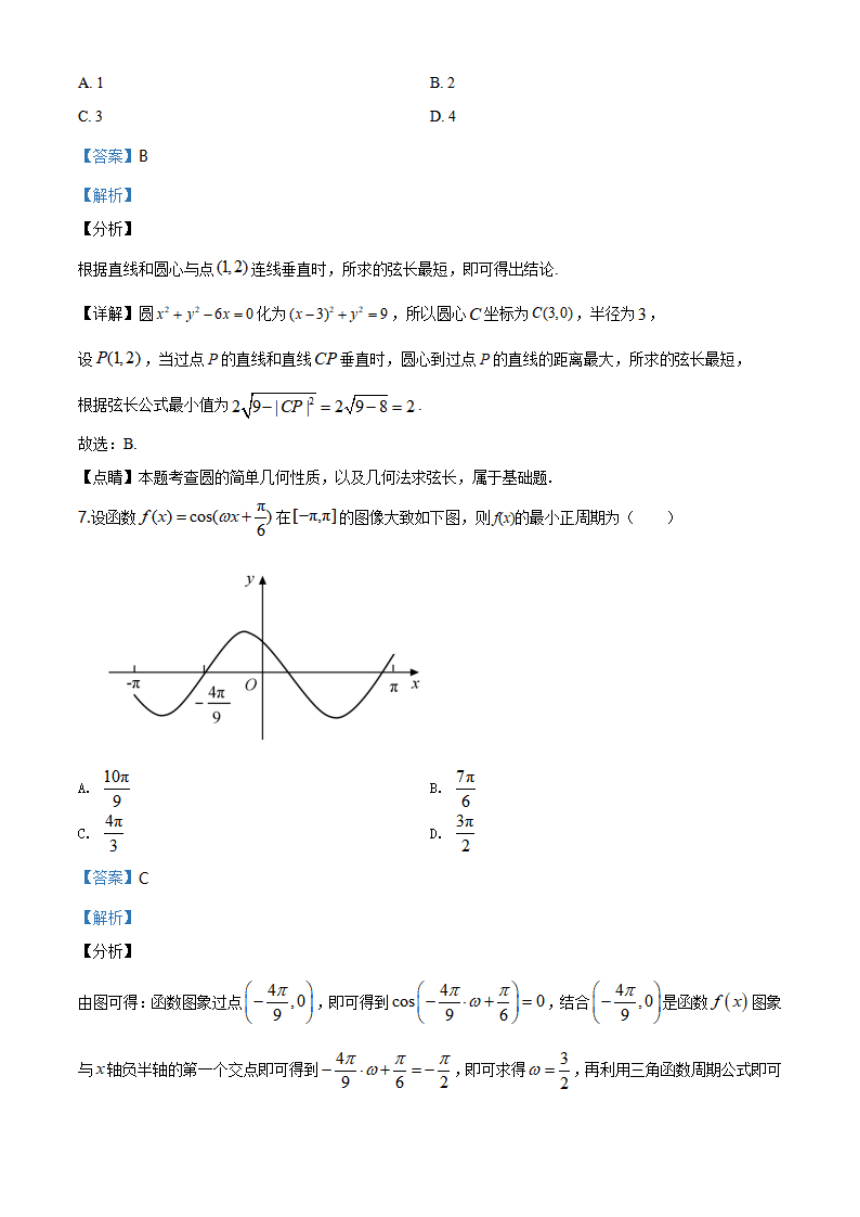
2020年普通高等学校招生全国统一考试
文科数学
注意事项
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑如需改动
用橡皮擦干净后,再选涂其他答案标号回答非选择题时,将答案写在答题卡上写在本试卷上
无效
3.考试结束后,将本试卷和答题卡并交回
选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有
项是符合题目要求的
1已知集合A={xx2-3x-4<0},B={41,3,5},则4∩B=()
A.{-4,1
B.{15
3S}
D.{13
【答案】D
【解析】
【分析】
首先解一元二次不等式求得集合A,之后利用交集中元素的特征求得4∩B,得到结果
【详解】由x2-3x-4<0解得-1
故选:D
【点晴】该题考查的是有关集合的问题,涉及到的知识点有利用一元二次不等式的解法求集合,集合的交
运算,属于基础题目
2若z=1+2i+,则=()
A.0
D.2
【答案】C
【解析】
【分析】
先根据2=-1将=化简,再根据向量的模的计算公式即可求出
【详解】因为z=1+2+P=1+2-1=1+1,所以=2+12=
【点晴】本题主要考查向量的模的计算公式的应用,属于容易题
3埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方
形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为
()
√+1
【答案】D
【解析】
【分析】
设CD=aPE=b,利用PO2=CDPE得到关于a,b的方程,解方程即可得到笞案
【详解】如图,设CD=a,PE=b,则PO=√PE2-OE
由题意PO=2
b,即b
ab,化简得4(-)2-2--1=0
解得2=1+√5(负值含去)
故选:C
【点晴】本题主要考查正四棱锥的概念及其有关计算,考查学生的数学计算能力,是一道容易题
4设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为()
2-54-5
【答案】A
【解析】
【分析】
歹出从5个点选3个点的所有情况,再列出3点共线的情况,用古典概型的概率计算公式运算即可
【详解】如图,从O,A,B,C,D5个点中任取3个有
104,
B1,10,
A,
C.0
4,
D.O,
B,
C
to,
B,
D
0,
C,
D,
A,
B,
C
4,
B,
D
AC2D}2{BC2D}共10种不同取法,
3点共线只有{AOC}与{B,O,D共2种情冫
由古典概型的概率计算公式知,
取到3点共线的概率为2
5
故选:A
同课章节目录
