2020年浙江卷数学高考真题试题(word版,无答案)
文档属性
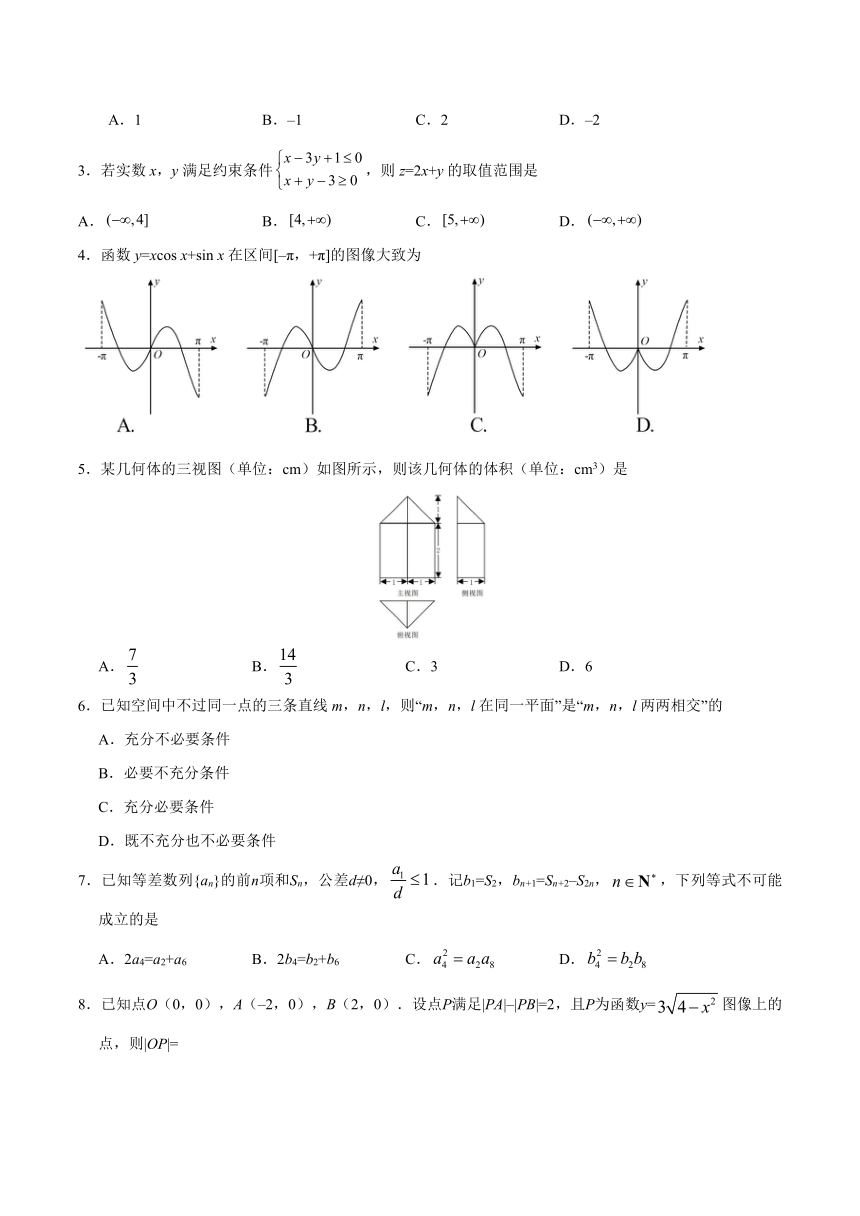
| 名称 | 2020年浙江卷数学高考真题试题(word版,无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 257.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-11 11:17:49 | ||
图片预览

文档简介
5.绝密★启用前
2020年普通高等学校招生全国统一考试(浙江卷)
数
学
本试题卷分选择题和非选择题两部分。全卷共4页,选择题部分1至2页;非选择题部分3至4页。满分150分。考试用时120分钟。
考生注意:
1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
参考公式:
如果事件A,B互斥,那么
如果事件A,B相互独立,那么
如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中事件A恰好发生k次的概率
台体的体积公式
其中分别表示台体的上、下底面积,表示台体的高
柱体的体积公式
其中表示柱体的底面积,表示柱体的高
锥体的体积公式
其中表示锥体的底面积,表示锥体的高
球的表面积公式
球的体积公式
其中表示球的半径
选择题部分(共40分)
一、选择题:本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合P=,Q=,则PQ=
A.
B.
C.
D.
2.已知a∈R,若a–1+(a–2)i(i为虚数单位)是实数,则a=
A.1
B.–1
C.2
D.–2
3.若实数x,y满足约束条件,则z=2x+y的取值范围是
A.
B.
C.
D.
4.函数y=xcos
x+sin
x在区间[–π,+π]的图像大致为
5.某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是
A.
B.
C.3
D.6
6.已知空间中不过同一点的三条直线m,n,l,则“m,n,l在同一平面”是“m,n,l两两相交”的
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
7.已知等差数列{an}的前n项和Sn,公差d≠0,.记b1=S2,bn+1=Sn+2–S2n,,下列等式不可能成立的是
A.2a4=a2+a6
B.2b4=b2+b6
C.
D.
8.已知点O(0,0),A(–2,0),B(2,0).设点P满足|PA|–|PB|=2,且P为函数y=图像上的点,则|OP|=
A.
B.
C.
D.
9.已知a,bR且ab≠0,若(x–a)(x–b)(x–2a–b)≥0在x≥0上恒成立,则
A.a<0
B.a>0
C.b<0
D.b>0
10.设集合S,T,SN
,TN
,S,T中至少有两个元素,且S,T满足:
①对于任意x,yS,若x≠y,都有xyT
②对于任意x,yT,若xA.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有4个元素
D.若S有3个元素,则S∪T有5个元素
非选择题部分(共110分)
二、填空题:本大题共7小题,共36分。多空题每小题6分,单空题每小题4分。
11.已知数列{an}满足,则S3=___▲____.
12.设,则a5=___▲___;a1+a2
+
a3=___▲____.
13.已知,则
▲
;
▲
.
14.已知圆锥展开图的侧面积为2π,且为半圆,则底面半径为
▲
.
15.设直线,圆,,若直线与,都相切,则
▲
;b=
▲
.
16.一个盒子里有1个红1个绿2个黄四个相同的球,每次拿一个,不放回,拿出红球即停,设拿出黄球的个数为,则
▲
;
▲
.
17.设,为单位向量,满足,,,设,的夹角为,则的最小值为
▲
.
三、解答题:本大题共5小题,共74分。解答应写出文字说明、证明过程或演算步骤。
18.(本题满分14分)
在锐角△ABC中,角A,B,C的对边分别为a,b,c,且.
(I)求角B;
(II)求cosA+cosB+cosC的取值范围.
19.(本题满分15分)
如图,三棱台DEF—ABC中,面ADFC⊥面ABC,∠ACB=∠ACD=45°,DC
=2BC.
(I)证明:EF⊥DB;
(II)求DF与面DBC所成角的正弦值.
20.(本题满分15分)
已知数列{an},{bn},{cn}中,.
(Ⅰ)若数列{bn}为等比数列,且公比,且,求q与an的通项公式;
(Ⅱ)若数列{bn}为等差数列,且公差,证明:.
21.(本题满分15分)
如图,已知椭圆,抛物线,点A是椭圆与抛物线的交点,过点A的直线l交椭圆于点B,交抛物线于M(B,M不同于A).
(Ⅰ)若,求抛物线的焦点坐标;
(Ⅱ)若存在不过原点的直线l使M为线段AB的中点,求p的最大值.
22.(本题满分15分)
已知,函数,其中e=2.71828…为自然对数的底数.
(Ⅰ)证明:函数在上有唯一零点;
(Ⅱ)记x0为函数在上的零点,证明:
(ⅰ);
(ⅱ).
2020年普通高等学校招生全国统一考试(浙江卷)
数
学
本试题卷分选择题和非选择题两部分。全卷共4页,选择题部分1至2页;非选择题部分3至4页。满分150分。考试用时120分钟。
考生注意:
1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
参考公式:
如果事件A,B互斥,那么
如果事件A,B相互独立,那么
如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中事件A恰好发生k次的概率
台体的体积公式
其中分别表示台体的上、下底面积,表示台体的高
柱体的体积公式
其中表示柱体的底面积,表示柱体的高
锥体的体积公式
其中表示锥体的底面积,表示锥体的高
球的表面积公式
球的体积公式
其中表示球的半径
选择题部分(共40分)
一、选择题:本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合P=,Q=,则PQ=
A.
B.
C.
D.
2.已知a∈R,若a–1+(a–2)i(i为虚数单位)是实数,则a=
A.1
B.–1
C.2
D.–2
3.若实数x,y满足约束条件,则z=2x+y的取值范围是
A.
B.
C.
D.
4.函数y=xcos
x+sin
x在区间[–π,+π]的图像大致为
5.某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是
A.
B.
C.3
D.6
6.已知空间中不过同一点的三条直线m,n,l,则“m,n,l在同一平面”是“m,n,l两两相交”的
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
7.已知等差数列{an}的前n项和Sn,公差d≠0,.记b1=S2,bn+1=Sn+2–S2n,,下列等式不可能成立的是
A.2a4=a2+a6
B.2b4=b2+b6
C.
D.
8.已知点O(0,0),A(–2,0),B(2,0).设点P满足|PA|–|PB|=2,且P为函数y=图像上的点,则|OP|=
A.
B.
C.
D.
9.已知a,bR且ab≠0,若(x–a)(x–b)(x–2a–b)≥0在x≥0上恒成立,则
A.a<0
B.a>0
C.b<0
D.b>0
10.设集合S,T,SN
,TN
,S,T中至少有两个元素,且S,T满足:
①对于任意x,yS,若x≠y,都有xyT
②对于任意x,yT,若x
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有4个元素
D.若S有3个元素,则S∪T有5个元素
非选择题部分(共110分)
二、填空题:本大题共7小题,共36分。多空题每小题6分,单空题每小题4分。
11.已知数列{an}满足,则S3=___▲____.
12.设,则a5=___▲___;a1+a2
+
a3=___▲____.
13.已知,则
▲
;
▲
.
14.已知圆锥展开图的侧面积为2π,且为半圆,则底面半径为
▲
.
15.设直线,圆,,若直线与,都相切,则
▲
;b=
▲
.
16.一个盒子里有1个红1个绿2个黄四个相同的球,每次拿一个,不放回,拿出红球即停,设拿出黄球的个数为,则
▲
;
▲
.
17.设,为单位向量,满足,,,设,的夹角为,则的最小值为
▲
.
三、解答题:本大题共5小题,共74分。解答应写出文字说明、证明过程或演算步骤。
18.(本题满分14分)
在锐角△ABC中,角A,B,C的对边分别为a,b,c,且.
(I)求角B;
(II)求cosA+cosB+cosC的取值范围.
19.(本题满分15分)
如图,三棱台DEF—ABC中,面ADFC⊥面ABC,∠ACB=∠ACD=45°,DC
=2BC.
(I)证明:EF⊥DB;
(II)求DF与面DBC所成角的正弦值.
20.(本题满分15分)
已知数列{an},{bn},{cn}中,.
(Ⅰ)若数列{bn}为等比数列,且公比,且,求q与an的通项公式;
(Ⅱ)若数列{bn}为等差数列,且公差,证明:.
21.(本题满分15分)
如图,已知椭圆,抛物线,点A是椭圆与抛物线的交点,过点A的直线l交椭圆于点B,交抛物线于M(B,M不同于A).
(Ⅰ)若,求抛物线的焦点坐标;
(Ⅱ)若存在不过原点的直线l使M为线段AB的中点,求p的最大值.
22.(本题满分15分)
已知,函数,其中e=2.71828…为自然对数的底数.
(Ⅰ)证明:函数在上有唯一零点;
(Ⅱ)记x0为函数在上的零点,证明:
(ⅰ);
(ⅱ).
同课章节目录
