北师大版九年级下册数学第二章二次函数整章同步教学课件(302张PPT)
文档属性
| 名称 | 北师大版九年级下册数学第二章二次函数整章同步教学课件(302张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 09:59:08 | ||
图片预览








文档简介
第二章 二次函数
数学·九年级下册·北师
1 二次函数
1.[2020上海长宁区一模]下列函数中,y是x的二次函数的是 ( )
A.y=1????2B.y=x2-1
C.y=3x+1 D.y=(x-1)2-x2
?
答案
1.B 【解析】 A项,y=1????2右边不是整式,故y不是x的二次函数;C项,y=3x+1是一次函数;D项,y=(x-1)2-x2=-2x+1,不是二次函数.故选B.
?
知识点1 二次函数的概念
判定一个函数是否为二次函数的方法
(1)先将函数进行整理,使其右边是含自变量的代数式,左边是因变量;(2)判定右边含自变量的代数式是否为整式;(3)判定含自变量的项的最高次数是否为2;(4)判定二次项的系数是否为0.
归纳总结
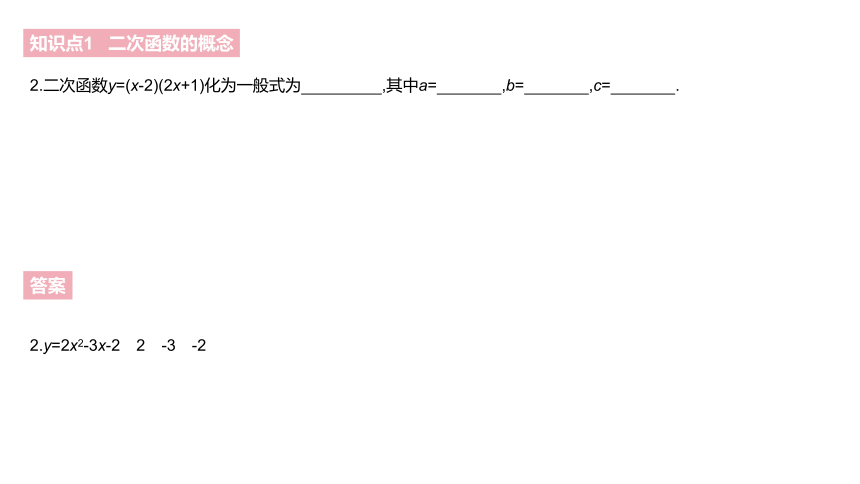
2.二次函数y=(x-2)(2x+1)化为一般式为 ,其中a= ,b= ,c= .?
答案
2.y=2x2-3x-2 2 -3 -2
知识点1 二次函数的概念
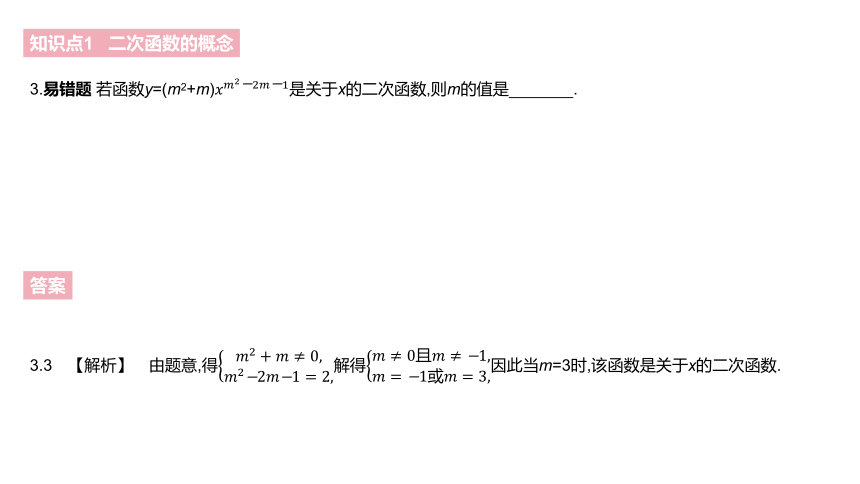
3.易错题 若函数y=(m2+m)????????2?2?????1是关于x的二次函数,则m的值是 .?
?
答案
3.3 【解析】 由题意,得????2+????≠0,????2?2?????1=2,解得????≠0且????≠?1,????=?1或????=3,因此当m=3时,该函数是关于x的二次函数.
?
知识点1 二次函数的概念
4.[2020浙江金华七校联考]已知关于自变量x的函数y=(m2-m)x2+(m-1)x+m+1.
(1)若该函数是一次函数,则m应满足什么条件?
(2)若该函数是二次函数,则m应满足什么条件?
答案
4.【解析】 (1)若该函数是一次函数,则????2?????=0,?????1≠0,
解得????=0或????=1,????≠1,所以m=0,
因此若该函数是一次函数,则m=0.
(2)若该函数是二次函数,则m2-m≠0,
解得m≠0且m≠1,
因此若该函数是二次函数,则m≠0且m≠1.
?
知识点1 二次函数的概念
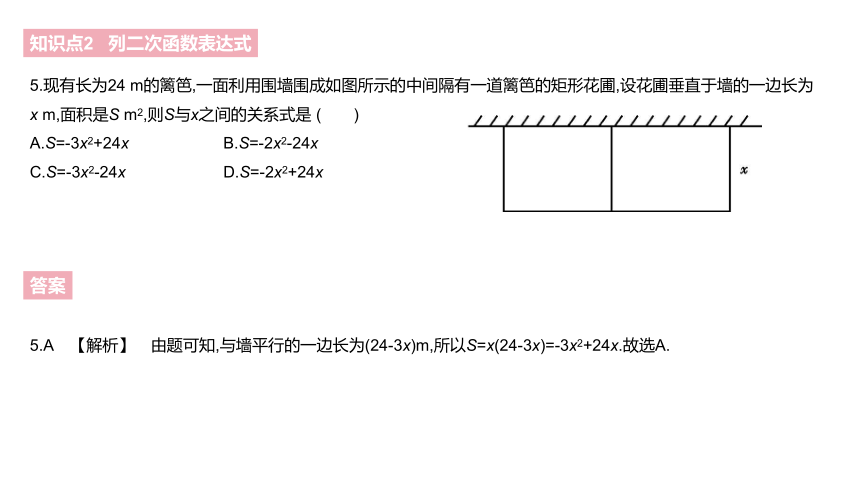
5.现有长为24 m的篱笆,一面利用围墙围成如图所示的中间隔有一道篱笆的矩形花圃,设花圃垂直于墙的一边长为
x m,面积是S m2,则S与x之间的关系式是 ( )?
A.S=-3x2+24x B.S=-2x2-24x
C.S=-3x2-24x D.S=-2x2+24x
答案
5.A 【解析】 由题可知,与墙平行的一边长为(24-3x)m,所以S=x(24-3x)=-3x2+24x.故选A.
知识点2 列二次函数表达式
6.[2020安徽芜湖一模]某工厂今年一月份生产防疫护目镜的产量是20万件,计划接下来两个月增加产量,如果月平均增长率为x,那么第一季度防疫护目镜的产量y(万件)与x之间的关系式为 .?
答案
6. y=20x2+60x+60 【解析】 由题意知,一月,二月,三月的产量分别为20万件,20(x+1)万件,20(x+1)2万件,所以第一季度防疫护目镜的产量y(万件)与x之间的关系式为y=20+20(x+1)+20(x+1)2=20x2+60x+60.
知识点2 列二次函数表达式
7.已知一个菱形两条对角线的长的和为24 cm,设其中一条对角线的长为x cm,则该菱形的面积S(cm2)与x(cm)之间的函数关系式为 ,自变量x的取值范围是 .?
答案
7.S=-12x2+12x 0-12x2+12x.∵????>0,24?????>0,∴0?
知识点2 列二次函数表达式
8.某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满;当每个房间每天的定价每增加10元时,就会有1个房间空闲.设每个房间每天的定价增加x元(x为10的整数倍).求:
(1)房间每天的入住量y(间)关于x(元)的函数表达式;
(2)该宾馆每天的房间收费z(元)关于x(元)的函数表达式.
答案
8.【解析】 (1)由题意,得y=-110x+60,
即房间每天的入住量y关于x的函数表达式为y=-110x+60(0≤x≤600,且x为10的整数倍).
(2)由题意,得z=(200+x)(-110x+60)=-110x2+40x+12 000,
即该宾馆每天的房间收费z关于x的函数表达式为z=-110x2+40x+12 000(0≤x≤600,且x为10的整数倍).
?
知识点2 列二次函数表达式
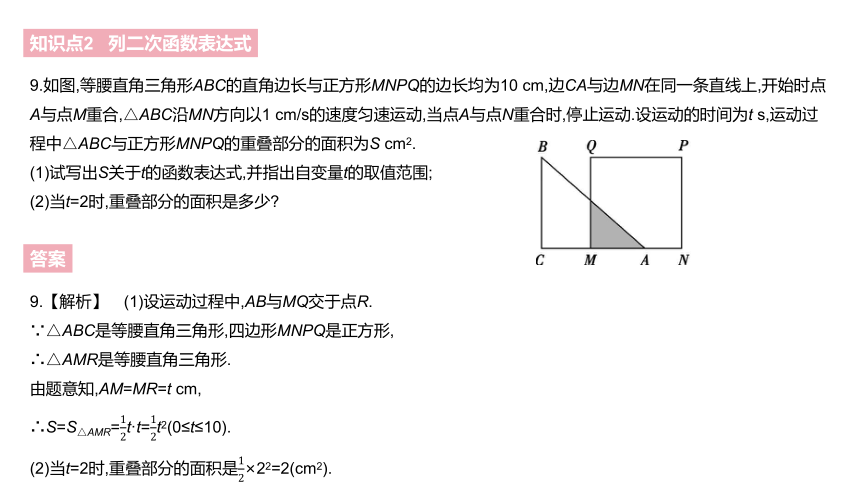
9.如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10 cm,边CA与边MN在同一条直线上,开始时点A与点M重合,△ABC沿MN方向以1 cm/s的速度匀速运动,当点A与点N重合时,停止运动.设运动的时间为t s,运动过程中△ABC与正方形MNPQ的重叠部分的面积为S cm2.
(1)试写出S关于t的函数表达式,并指出自变量t的取值范围;
(2)当t=2时,重叠部分的面积是多少?
答案
9.【解析】 (1)设运动过程中,AB与MQ交于点R.
∵△ABC是等腰直角三角形,四边形MNPQ是正方形,
∴△AMR是等腰直角三角形.
由题意知,AM=MR=t cm,
∴S=S△AMR=12t·t=12t2(0≤t≤10).
(2)当t=2时,重叠部分的面积是12×22=2(cm2).
?
知识点2 列二次函数表达式
2 二次函数的图象与
性质
课时1 二次函数y=x2,y=-x2的图象与性质
课时1
1.已知正方形的边长为x cm,则它的面积y(cm2)与边长x(cm)的函数图象为 ( )
答案
1.C 【解析】 根据正方形面积公式可知,函数表达式为y=x2,其中x>0.故选C.
知识点1 二次函数y=x2的图象与性质
2.已知二次函数y=x2的图象经过点(1,y1),(2,y2),则y1,y2的大小关系是 ( )
A.y1=y2 B.y1>y2
C.y1?
答案
2.C 【解析】 对于二次函数y=x2,当x>0时,y的值随x值的增大而增大,因为1<2,所以y1?
知识点1 二次函数y=x2的图象与性质
3.关于函数y=x2,下列说法正确的是 ( )
A.y的值随着x的增大而增大
B.y的值随着x的增大而减小
C.函数有最小值
D.无论x取何值,y的值总为正
答案
3.C 【解析】 对于函数y=x2,当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大,故A,B错误;当x=0时,y=0,函数有最小值,故D错误,C正确.故选C.
知识点1 二次函数y=x2的图象与性质
4.若点A(2,m)在二次函数y=x2的图象上,则m= ,点A关于x轴的对称点B的坐标是 ,点A关于y轴的对称点C的坐标是 ,B,C两点中在抛物线y=x2上的点是 .?
答案
4.4 (2,-4) (-2,4) C
知识点1 二次函数y=x2的图象与性质
5.下列各点中,在二次函数y=-x2图象上的是 ( )
A.(23,-6) B.(-23,6)
C.(-23,12) D.(23,-12)
?
答案
5.D 【解析】 当x=23时,y=-(23)2=-12,故点(23,-12)在二次函数y=-x2的图象上.故选D.
?
知识点2 二次函数y=-x2的图象与性质
判断点是否在函数图象上的方法
将点的横坐标代入函数表达式,若求出的函数值等于该点的纵坐标,则该点在函数图象上;若求出的函数值不等于该点的纵坐标,则该点不在函数图象上.
归纳总结
6.[2019海南海口龙华区期中]抛物线y=-x2不具有的性质是 ( )
A.开口向下 B.对称轴是y轴
C.与y轴不相交 D.最高点是原点
答案
6.C 【解析】 抛物线y=-x2与y轴相交于坐标原点(0,0).故选C.
知识点2 二次函数y=-x2的图象与性质
7.关于二次函数y=x2和y=-x2的图象,以下说法正确的有 .(填序号)?
①两图象都关于x轴对称;②两图象都关于y轴对称;③两图象的顶点相同;④两图象的开口方向不同;⑤点(-1,1)在抛物线y=x2上,也在抛物线y=-x2上.
答案
7.②③④ 【解析】 因为二次函数y=x2的图象开口向上,对称轴是y轴,顶点坐标是(0,0),二次函数y=-x2的图象开口向下,对称轴是y轴,顶点坐标是(0,0),所以②③④正确,①不正确;把点(-1,1)分别代入y=x2和y=-x2验证,可知点(-1,1)在抛物线y=x2上,不在抛物线y=-x2上,所以⑤不正确.
知识点2 二次函数y=-x2的图象与性质
(1)对于二次函数的研究,一般从图象的开口方向、顶点坐标、对称轴,以及函数增减性、最大(小)值等方面展开;(2)二次函数y=x2和y=-x2的图象关于x轴对称.
名师点睛
8.二次函数y=-x2图象的顶点坐标是 ,若点(a,-4)在其图象上,则a的值是 .?
答案
8.(0,0) ±2 【解析】 二次函数y=-x2图象的顶点坐标是(0,0),∵点(a,-4)在其图象上,∴-a2=-4,解得a=±2.
知识点2 二次函数y=-x2的图象与性质
9.函数y=x2与y=-x2的图象关于 对称,也可以认为函数y=-x2的图象是由函数y=x2的图象绕 旋转后得到的.?
答案
9.x轴 原点
知识点2 二次函数y=-x2的图象与性质
10.已知点A(-2,m),B(3,n)都是抛物线y=-x2上的点,则m与n的大小关系是 .?
答案
10.m>n 【解析】 由题意知,m=-(-2)2=-4,n=-32=-9,所以m>n.
知识点2 二次函数y=-x2的图象与性质
11.已知函数y=????2????????2?2是关于x的二次函数.
(1)求满足条件的k的值;
(2)当k为何值时,抛物线有最高点?求出这个最高点,并求x为何值时,y随x的增大而增大?
(3)当k为何值时,函数有最小值?最小值是多少?并求x为何值时,y随x的增大而减小?
?
知识点2 二次函数y=-x2的图象与性质
答案
11.【解析】 (1)∵函数y=????2????????2?2是关于x的二次函数,
∴k2-2=2,且????2≠0,
∴k=±2.
(2)当抛物线有最高点时,
图象开口向下,即????2<0,
∴k=-2,
∴最高点为(0,0),当x<0时,y随x的增大而增大.
(3)当函数有最小值时,
图象开口向上,即????2>0,
∴k=2,
∴最小值为0,当x<0时,y随x的增大而减小.
?
知识点2 二次函数y=-x2的图象与性质
12.已知点M(-2,m)在抛物线y=-x2上,过点M作MN∥x轴,交抛物线于另一点N,求△MON的面积.
答案
12.【解析】 将点M(-2,m)代入抛物线y=-x2,得m=-4,
∴点M(-2,-4).
∵MN∥x轴,点M,N在抛物线上,
∴点M,N关于y轴对称,∴N(2,-4),MN=4,
∴S△MON=12×4×4=8.
?
知识点2 二次函数y=-x2的图象与性质
1.在同一平面直角坐标系中,二次函数y=x2与一次函数y=-x-1的图象大致为 ( )
答案
1.D
2.[2019湖北咸宁中考]已知点A(-1,m),B(1,m),C(2,m-n)(n>0)在同一个函数的图象上,这个函数可能是 ( )
A.y=xB.y=-2????
C.y=x2D.y=-x2
?
答案
2.D 【解析】 ∵A(-1,m),B(1,m),∴点A与点B关于y轴对称.∵n>0,∴m-n3.如图,Rt△ABC的三个顶点A,B,C均在函数y=x2的图象上,并且斜边AB平行于x轴,若斜边上的高为h,则 ( )
A.h<1 B.h=1 C.1答案
3.B 【解析】 如图,过点C作CE⊥AB于点E,设斜边AB交y轴于点D,连接CD.由题意设A(-a,a2)(a>0),B(a,a2),C(b,b2)
(b>0),D(0,a2),则斜边上的高为h=a2-b2.∵△ABC是直角三角形,∴CD=a,在Rt△CDE中,CE2+DE2=CD2,即h2+b2=a2,
∴h2=h,∴h=1.故选B.
4.[2019湖南衡阳中考]在平面直角坐标系中,抛物线y=x2如图所示.已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4??依次进行下去,则点A2 019的坐标为 .?
答案
4.(-1 010,1 0102) 【解析】 易知点A,A1关于y轴对称,点A2,A3关于y轴对称??点A1的坐标为(-1,1),∴直线A1A2的表达式为y=x+2,令x+2=x2,解得x1=-1(舍去),x2=2,故点A2的坐标为(2,4),∴点A3的坐标为(-2,4).同理可得A5(-3,9)??以此类推,可知点An(n为奇数)的坐标为(-????+12,(????+12)2),故点A2 019的坐标为(-1 010,1 0102).
?
5.定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1①y=2x; ②y=-x2; ③y=x2(x>0); ④y=-1????.
?
答案
5.①③
6.如图,圆的半径为2,C1是二次函数y=x2的图象,C2是二次函数y=-x2 的图象,则阴影部分的面积是 .?
答案
6.2π 【解析】 由二次函数y=x2和y=-x2的图象关于x轴对称,可知阴影部分的面积即圆面积的一半,所以阴影部分的面积是12π×22=2π.
?
7.已知a>1,点(a-1,y1),(a,y2),(a+1,y3)都在二次函数y=x2的图象上,则y1,y2,y3之间的大小关系为 .?
答案
7.y3>y2>y1 【解析】 因为a>1,所以00时,y的值随x值的增大而增大,所以y1,y2,y3之间的大小关系为y3>y2>y1.
8.如图,正方形OABC的顶点B在抛物线y=x2上,且点B在第一象限,若点B的横坐标与纵坐标之和等于6,则正方形OABC的面积为 .?
答案
8.10 【解析】 因为正方形OABC的顶点B在抛物线y=x2上,且点B在第一象限,所以可设点B的坐标为(x,x2),x>0.因为点B的横坐标与纵坐标之和等于6,所以x+x2=6,解得x1=2,x2=-3(不合题意,舍去),所以B(2,4),所以OB2=22+42=20.因为OB2=OA2+AB2,OA=AB,所以正方形OABC的边长为10,所以正方形OABC的面积为OA2=10.
?
9.已知抛物线y=-x2与直线y=3x+m都经过点(2,n).
(1)画出函数y=-x2的图象,并求出m,n的值;
(2)两者是否存在另一个交点?若存在,请求出这个点的坐标;若不存在,请说明理由.
答案
9.【解析】 (1)函数y=-x2的图象如图所示.
∵抛物线y=-x2与直线y=3x+m都经过点(2,n),
∴n=-22,n=3×2+m,∴n=-4,m=-10.
(2)存在.
由题意得,????=3?????10,????=?????2,
解得????=?5,????=?25,或????=2,????=?4,
∴另一个交点的坐标为(-5,-25).
?
课时2 二次函数y=ax2,y=ax2+c的图象与性质
课时2
1.[2020上海闵行区模拟]若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点 ( )
A.(2,4) B.(-2,-4)
C.(-4,2) D.(4,-2)
答案
1.A 【解析】 因为二次函数y=ax2的图象的对称轴为y轴,所以若图象经过点P(-2,4),则该图象必经过点(2,4).故选A.
知识点1 二次函数y=ax2的图象与性质
2.易错题 若抛物线y=m????????2+????的开口向下,则m的值为 ( )
A.-1 B.-2
C.1 D.1或-2
?
答案
2.B 【解析】 根据题意,得m2+m=2且m<0,∴m=-2.故选B.
知识点1 二次函数y=ax2的图象与性质
3.关于抛物线y=12x2,y=x2,y=-x2,给出下列结论:①都是开口向上;②都以点(0,0)为顶点;③都以y轴为对称轴;④都关于x轴对称.其中正确的个数有( )
A.1 B.2 C.3 D.4
?
答案
3.B 【解析】 抛物线y=12x2,y=x2开口向上,y=-x2开口向下,所以①错误;抛物线y=12x2,y=x2,y=-x2都以点(0,0)为顶点,都以y轴为对称轴,所以②③正确,④错误.故选B.
?
知识点1 二次函数y=ax2的图象与性质
4.[2020山东德州模拟]给出下列函数:①y=3x+2;②y=3????;③y=2x2;④y=-3x2.其中符合条件“当x>1时,函数值y随自变量x增大而增大”的是 ( )
A.①③ B.③④ C.②④ D.②③
?
答案
4.A 【解析】 ①y=3x+2,当x>1时,函数值y随自变量x增大而增大,故①符合题意.②y=3????,当x>1时,函数值y随自变量x增大而减小,故②不符合题意.③y=2x2,当x>1时,函数值y随自变量x增大而增大,故③符合题意.④y=-3x2,当x>1时,函数值y随自变量x增大而减小,故④不符合题意.故选A.
?
知识点1 二次函数y=ax2的图象与性质
5.[2020内蒙古呼和浩特期中]已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是 .(请用“>”连接)?
答案
5. a1>a2>a3>a4 【解析】 由题图,可知抛物线y=a1x2与y=a2x2的开口向上,其中前者开口小,所以a1>a2>0,抛物线y=a3x2与y=a4x2的开口向下,其中后者开口小,所以a4a2>a3>a4.
知识点1 二次函数y=ax2的图象与性质
6.若点A(x1,4),B(x2,4)(x1≠x2)均在抛物线y=ax2上,则当x=x1+x2时,y的值是 .?
答案
6.0 【解析】 由题可知,点A,B关于y轴对称,所以x=x1+x2=0,故y的值为0.
知识点1 二次函数y=ax2的图象与性质
7.函数y=x2+1的图象大致是 ( )
答案
7.C 【解析】 函数y=x2+1的图象开口向上,顶点是(0,1).故选C.
知识点2 二次函数y=ax2+c的图象与性质
8.[2020浙江杭州期末]关于二次函数y=-2x2-2,下列说法正确的是 ( )
A.图象开口向上
B.当x<0时,y随x的增大而增大
C.图象的对称轴是x=1
D.当x=0时,y有最大值-12
?
答案
8.B 【解析】 因为二次函数y=-2x2-2,a=-2<0,所以该函数图象开口向下,当x<0时,y随x的增大而增大,故A错误,B正确;二次函数y=-2x2-2图象的对称轴是x=0,顶点坐标为(0,-2),所以当x=0时,y有最大值-2,故C,D错误.故选B.
知识点2 二次函数y=ax2+c的图象与性质
9.已知直线y=2x与抛物线y=ax2+3的一个交点为(2,b).
(1)求a,b的值;
(2)若直线y=2x上纵坐标为2的点为A,抛物线y=ax2+3的顶点为B,求△AOB的面积S.
答案
9.【解析】 (1)∵点(2,b)在直线y=2x上,∴b=4.
∵点(2,b)即点(2,4)在抛物线y=ax2+3上,
∴4a+3=4,∴a=14.
(2)在y=2x中,令y=2,得x=1,∴A(1,2),
又∵抛物线y=14x2+3的顶点为B(0,3),
∴△AOB的面积S=12×3×1=32.
?
知识点2 二次函数y=ax2+c的图象与性质
10.[2020江苏盐城期末]把抛物线y=12x2向下平移2个单位长度,得到的抛物线的表达式为 ( )
A.y=12x2+2 B.y=12x2-2
C.y=12(x+2)2?D.y=12(x-2)2
?
答案
10.B 【解析】 二次函数y=12x2的顶点坐标为(0,0),向下平移2个单位长度得对应点的坐标为(0,-2),所以平移后抛物线的表达式为y=12x2-2.故选B.
?
知识点3 二次函数y=ax2+c与y=ax2的图象之间的关系
11.已知二次函数y=ax2+c与y=-5x2的图象形状相同、方向相反,且其顶点坐标是(0,3),则其表达式为 .?
答案
11.y=5x2+3 【解析】 ∵二次函数y=ax2+c与y=-5x2的形状相同、方向相反,∴a=5.∵抛物线的顶点坐标是(0,3),∴c=3,∴其表达式为y=5x2+3.
知识点3 二次函数y=ax2+c与y=ax2的图象之间的关系
12.易错题 能否通过适当地上下平移二次函数y=13x2的图象,使得到的新的函数图象过点(3,-3)?若能,说出平移的方向和距离;若不能,说明理由.
?
答案
12.【解析】 能.
把函数y=13x2的图象向下平移6个单位长度,得到的图象对应的函数表达式为y=13x2-6,该函数的图象过点(3,-3).
?
知识点3 二次函数y=ax2+c与y=ax2的图象之间的关系
1.在同一平面直角坐标系中,y关于x的一次函数y=-mx+n2与二次函数y=x2+m的图象可能是 ( )
答案
1.D
解答双图象问题的方法
(1)分类讨论法:根据函数表达式中系数的正负分类讨论.(2)逐项排除法:假定选项中的某一个函数图象正确,然后判断另一个函数图象是否合理;或根据两函数图象确定系数的取值范围,取值范围相同的正确,取值范围不同的错误.
归纳总结
2.易错题 已知拋物线y=-13x2+2,当1≤x≤5时,y的最大值是 ( )
A.2 B.23 C.53 D.73
?
答案
2.C 【解析】 ∵拋物线y=-13x2+2的二次项系数a=-13<0,∴该抛物线的开口向下,又∵其对称轴就是y轴,∴当1≤x≤5时,拋物线y=-13x2+2是下降的,∴当x=1时,y取得最大值,y最大=-13+2=53.故选C.
?
3.点A(-1,y1),B(2,y2),C(3,y3)都在二次函数y=(a2+1)x2+2的图象上,则y1,y2,y3的大小关系是 ( )
A.y1y2>y3
C.y1>y3>y2 D.y2答案
3.A 【解析】 因为a2+1>0,所以y=(a2+1)x2+2的图象开口向上,又因为对称轴为y轴,所以当x>0时,y随x的增大而增大.因为A(-1,y1)关于y轴的对称点的坐标为(1,y1),且1<2<3,所以y14.如图,两条抛物线y1=-12x2+1,y2=-12x2-1与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为 ( )?
A.10 B.8 C.6 D.4
?
答案
4.B 【解析】 如图,∵两抛物线表达式的二次项系数相同,∴两抛物线的形状完全相同.过抛物线y2=-12x2-1的顶点(0,-1)作平行于x轴的直线与抛物线y1=-12x2+1围成封闭图形,过点(0,-3)作平行于x轴的直线与抛物线y2=-12x2-1围成封闭图形,则这两个封闭图形的面积相等,故所求阴影部分的面积为4×2=8.故选B.
?
5.[2020安徽蚌埠期中]已知抛物线y=14x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等.如图,点M的坐标为(3,3),P是抛物线y=14x2+1上的一个动点,则△PMF周长的最小值是 ( )?
A.3 B.4 C.5 D.6
?
答案
5.C 【解析】 过点P作PE⊥x轴于点E,由题意可知,FP=PE,∴当点M,P,E三点共线时(如图所示),△PMF周长最小.易知ME∥y轴,∵F(0,2),M(3,3),∴ME=3,FM=(3?0)2+(3?2)2=2,∴△PMF周长的最小值为MP+FP+FM=ME+
FM=3+2=5.故选C.
?
6.已知抛物线y=mx2+m-2的顶点在y轴的负半轴上,且开口向上,则m的取值范围是 .?
答案
6.00,∴m的取值范围是07.关于二次函数y=-ax2-3,下列说法不正确的是 .(填序号)?
①只有当x=0时,y才有最大(或最小)值;②对于一切x的值,y都是负数;③当a>0时,y随x的增大而减小;④当a<0时,y随x的增大而减小.
答案
7.②③④ 【解析】 当x=0时,y有最大(或最小)值,且最大(或最小)值是-3,①正确;当a<0时,y的值可能为正数,②不正确;当a>0,x<0时,y随x的增大而增大,③不正确;当a<0,x>0时,y随x的增大而增大,④不正确.综上,不正确的是②③④.
8.已知抛物线y=x2-k的顶点为P,与x轴交于点A,B,且△ABP是等边三角形,则k的值是 .?
答案
8.3 【解析】 如图,由题意可知,k>0,点P的坐标为(0,-k),PO=k,OA=OB,AB=AP=BP,∠OPB=30°,∴tan 30°=????????????????,即????????????=33,解得OB=33k,∴点B的坐标为(33k,0).∵点B在抛物线y=x2-k上,∴将(33k,0)代入y=x2-k,得(33k)2-k=0,解得k1=0(不合题意,舍去),k2=3.故k的值为3.
?
9.已知二次函数y=mx2+1与反比例函数y=????????的图象有一个公共点(-1,-1).
(1)求二次函数和反比例函数的表达式;
(2)能否找到自变量x的取值范围,使二次函数、反比例函数的函数值都随x值的增大而减小?若能,写出这个取值范围;若不能,说明理由.
?
答案
9.【解析】 (1)因为两个函数的图象有一个公共点(-1,-1),
所以-1=m×(-1)2+1,-1=?????1,
所以m=-2,k=1,
所以二次函数的表达式为y=-2x2+1,反比例函数的表达式为y=1????.?
(2)能.
如图所示是二次函数y=-2x2+1和反比例函数y=1????在同一平面直角坐标系中的图象,
根据图象可知存在这样的自变量x的取值范围,
即当x>0时,二次函数、反比例函数的函数值都随x值的增大而减小.
?
10.如图,抛物线y=-12x2+2与x轴交于A,B两点,其中点A在x轴的正半轴上,点B在x轴的负半轴上.
(1)试写出该抛物线的对称轴和顶点C的坐标;
(2)在抛物线上是否存在一点M,使△MAC≌△OAC?若存在,求出点M的坐标;若不存在,请说明理由.
?
答案
10.【解析】 (1)抛物线的对称轴是y轴,顶点C的坐标为(0,2).
(2)不存在.理由如下:
由已知条件易得点A的坐标为(2,0),点B的坐标为(-2,0),
则OA=OB=OC=2,故三角形OAC是等腰直角三角形.
假设存在一点M,使△MAC≌△OAC,
因为AC为公共边,OA=OC,
所以点M和O关于直线AC对称,
因此四边形OAMC是正方形,所以点M的坐标为(2,2).
当x=2时,y=-12x2+2=-12×22+2=0≠2,
即点M不在抛物线y=-12x2+2上,
所以在抛物线上不存在一点M,使得△MAC≌△OAC.
?
课时3 二次函数y=a(x-h)2,y=a(x-h)2+k的图象与性质
课时3
1.二次函数y=3(x-2)2的图象的对称轴是( )
A.直线x=2 B.直线x=-2
C.y轴 D.x轴
答案
1.A
知识点1 二次函数y=a(x-h)2的图象与性质
2.二次函数y=3(x+1)2的图象不经过的象限是 ( )
A.第一、二象限 B.第二、四象限
C.第三、四象限 D.第二、三象限
答案
2.C 【解析】 因为二次函数y=3(x+1)2的图象开口向上,顶点为(-1,0),对称轴是直线x=-1,与y轴的交点是(0,3),所以二次函数y=3(x+1)2的图象经过第一、二象限,不经过第三、四象限.故选C.
知识点1 二次函数y=a(x-h)2的图象与性质
3.[2020河南焦作一模]若抛物线y=2(x-1)2经过(m,n)和(m+3,n)两点,则n的值为 ( )
A.92 B.-92 C.1 D.-12
?
答案
3.A 【解析】 由抛物线y=2(x-1)2经过(m,n)和(m+3,n)两点,可知该抛物线的对称轴为直线x=????+????+32=1,所以m=-12,将点(-12,n)代入函数表达式,得n=2(-12-1)2=92.故选A.
?
知识点1 二次函数y=a(x-h)2的图象与性质
4.[2020湖北鄂州期中]对于抛物线y=35(x-1)2,给出下列说法:①顶点坐标为(1,0);②对称轴为直线x=0;③有最低点;④当x>1时,y的值随x值的增大而增大;⑤当x=1时,y取最大值0.
其中正确的是 .(填序号)?
?
答案
4.①③④ 【解析】 因为抛物线y=35(x-1)2,所以顶点坐标为(1,0),对称轴为直线x=1,开口向上,有最低点,当x=1时,y取最小值0,当x>1时,y的值随x值的增大而增大,当x<1时,y的值随x值的增大而减小.故说法正确的是①③④.
?
知识点1 二次函数y=a(x-h)2的图象与性质
5.已知二次函数y=a(x-h)2,当x=2时,有最大值,且图象过点(1,-3),求该函数的表达式,并指出当x为何值时,y随x的增大而减小.
答案
5.【解析】 ∵当x=2时,二次函数y=a(x-h)2有最大值,
∴h=2,a<0,
又∵函数图象过点(1,-3),∴-3=a(1-2)2,解得a=-3,
∴该函数的表达式为y=-3(x-2)2.
当x>2时,y随x的增大而减小.
知识点1 二次函数y=a(x-h)2的图象与性质
6.[2020北京海淀区一模]将抛物线y=2x2向左平移3个单位长度后,所得到的抛物线的函数表达式为 ( )
A.y=2x2-3 B.y=2x2+3
C.y=2(x-3)2 D.y=2(x+3)2
答案
6.D 【解析】 抛物线y=2x2的顶点坐标为(0,0),向左平移3个单位长度后,顶点坐标变为(-3,0),所以平移后的抛物线的函数表达式为y=2(x+3)2.故选D.
知识点2 二次函数y=a(x-h)2,y=a(x-h)2+k与y=ax2的图象之间的关系
7.[2020黑龙江哈尔滨中考]将抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,所得到的抛物线的表达式为 ( )
A.y=(x+3)2+5 B.y=(x-3)2+5
C.y=(x+5)2+3 D.y=(x-5)2+3
答案
7.D 【解析】 解法一 根据抛物线的平移规律“左加右减(自变量),上加下减(常数项)”可知,抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,得到抛物线y=(x-5)2+3.
解法二 易知抛物线y=x2的顶点坐标是(0,0),将点(0,0)向上平移3个单位长度,再向右平移5个单位长度,得到点(5,3),即平移后抛物线的顶点坐标是(5,3),所以平移后得到抛物线y=(x-5)2+3.
知识点2 二次函数y=a(x-h)2,y=a(x-h)2+k与y=ax2的图象之间的关系
8.二次函数y=(x+2)2-1的图象大致为 ( )
答案
8.D 【解析】 抛物线y=(x+2)2-1的顶点坐标为(-2,-1),且开口向上.故选D.
知识点3 二次函数y=a(x-h)2+k的图象与性质
9.[2019甘肃兰州中考]已知点A(1,y1),B(2,y2)在抛物线y=-(x+1)2+2上,则下列结论正确的是 ( )
A.2>y1>y2 B.2>y2>y1
C.y1>y2>2 D.y2>y1>2
答案
9.A 【解析】 解法一 函数y=-(x+1)2+2有最大值2,图象开口向下,当x>-1时,y随x的增大而减小.∵-1<1<2,
∴2>y1>y2. 故选A.
解法二 函数y=-(x+1)2+2有最大值2,当x=1时,y1=-(1+1)2+2=-2;当x=2时,y2=-(2+1)2+2=-7,∴2>y1>y2.故选A.
知识点3 二次函数y=a(x-h)2+k的图象与性质
10.[2020安徽亳州二调]如果抛物线y=(x-m)2+m+1的对称轴是直线x=1,那么它的顶点坐标为 .?
答案
10.(1,2) 【解析】 ∵抛物线y=(x-m)2+m+1的对称轴是直线x=1,∴m=1,∴抛物线的表达式为y=(x-1)2+2,∴顶点坐标为(1,2).
知识点3 二次函数y=a(x-h)2+k的图象与性质
11.对于抛物线y=-12(x+3)2-1,给出下列说法:①抛物线的开口向下;②对称轴为直线x=3;③顶点坐标为(-3,1);④当x>3时,y随x的增大而减小.其中正确的有 .(填序号)?
?
答案
11.①④ 【解析】 因为a<0,所以抛物线开口向下,①正确;抛物线对称轴为直线x=-3,②错误;顶点坐标为(-3,-1),
③错误;当x>-3时,y随x的增大而减小,对于x>3时当然也成立,④正确.故正确的有①④.
知识点3 二次函数y=a(x-h)2+k的图象与性质
12.如图是二次函数y=(x+m)2+k的图象,其顶点为点M(1,-4).
(1)求二次函数的图象与x轴的交点A,B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=54S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
?
知识点3 二次函数y=a(x-h)2+k的图象与性质
答案
12.【解析】 (1)∵(1,-4)是二次函数y=(x+m)2+k图象的顶点坐标,
∴y=(x-1)2-4=x2-2x-3.
令y=0,则x2-2x-3=0,解得x1=-1,x2=3,
∴A,B两点的坐标分别为(-1,0),(3,0).
(2)在二次函数的图象上存在点P,使S△PAB=54S△MAB.
设点P(x,y),由(1)知AB=4,
则S△PAB=12AB×|y|=2|y|,
∵S△MAB=12AB×|-4|=8,
∴2|y|=54×8,解得y=±5.
?
知识点3 二次函数y=a(x-h)2+k的图象与性质
答案
∵二次函数的最小值为-4,∴y=5.
当y=5时,x=-2或x=4.
故存在点P,使S△PAB=54S△MAB,点P的坐标为(-2,5)或(4,5).
?
知识点3 二次函数y=a(x-h)2+k的图象与性质
1.[2019河北唐山路南区期中]抛物线y=(x+2)2+m2+1(m为常数)的顶点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
1.B 【解析】 ∵y=(x+2)2+m2+1,∴顶点坐标为(-2,m2+1),∵-2<0,m2+1>0,∴顶点在第二象限.故选B.
2.[2020黑龙江哈尔滨平房区一模]已知抛物线y=(x+2)2-1向左平移h个单位长度,向下平移k个单位长度,得到的抛物线的表达式为y=(x+3)2-4,则h和k的值分别为 ( )
A.1,3 B.3,-4 C.1,-3 D.3,-3
答案
2.A 【解析】 解法一 因为抛物线y=(x+2)2-1的顶点坐标是(-2,-1),所以向左平移h个单位长度,向下平移k个单位长度后的坐标为(-2-h,-1-k),所以平移后抛物线的表达式为y=(x+2+h)2-1-k.因为平移后抛物线的表达式为y=(x+3)2-4,所以2+h=3,-k-1=-4,所以h=1,k=3.故选A.
解法二 根据抛物线的平移规律“左加右减,上加下减”得到平移后的抛物线为y=(x+2+h)2-1-k=(x+3)2-4,所以2+h=3,-1-k=-4,所以h=1,k=3.故选A.
3.已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象是 ( )
答案
3.A 【解析】 因为二次函数的图象开口向上,所以a>0.因为二次函数的图象的顶点坐标为(1,-c),且由图象知,顶点在第四象限,所以c>0,故一次函数y=ax+c的图象经过第一、二、三象限.故选A.
4.已知二次函数y=3(x+1)2-4的图象上有三点A(-2,y1),B(1,y2),C(2,y3),则y1,y2,y3的大小关系为 ( )
A.y1>y2>y3 B.y2>y1>y3
C.y3>y2>y1 D.y3>y1>y2
答案
4.C 【解析】 由抛物线的对称性可知,点A(-2,y1)在抛物线上的对称点为A'(0,y1),对于抛物线y=3(x+1)2-4,当x>-1时,y随x的增大而增大,所以y3>y2>y1.故选C.
5.[2020浙江温州模拟]已知抛物线y=a(x-2)2+1经过点A(m,y1),B(m+2,y2),若点A在抛物线对称轴的左侧,且1A.0答案
5.C 【解析】 因为抛物线y=a(x-2)2+1的顶点坐标为(2,1),且12,????+2?2>2?????,解得1?
6.易错题已知二次函数y=-(x-h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为-1,则h的值为 ( )
A.3或6 B.1或6 C.1或3 D.4或6
答案
6.B 【解析】 如图,分h<2,2≤h≤5和h>5三种情况讨论.当h<2时,有-(2-h)2=-1,解得h1=1,h2=3(舍去).当2≤h≤5时,y=-(x-h)2的最大值为0,不符合题意.当h>5时,有-(5-h)2=-1,解得h3=4(舍去),h4=6.综上所述,h的值为1或6.故选B.
7.把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的函数表达式为 .?
答案
7.y=-(x+1)2-2 【解析】 二次函数y=(x-1)2+2图象的顶点坐标为(1,2),绕原点旋转180°后顶点坐标变为(-1,-2),所以旋转后得到的图象的函数表达式为y=a(x+1)2-2,因为旋转过程中开口大小不变,仅开口方向改变,所以a=-1,即旋转后得到的图象的函数表达式为y=-(x+1)2-2.
8.已知二次函数y=-(x-m)2+1,当x>3时,y随x的增大而减小,则m的取值范围是 .?
答案
8.m≤3 【解析】 对于二次函数y=-(x-m)2+1,当x>m时,y随x的增大而减小,结合题意可知m≤3.
9.如图,把抛物线y=x2沿直线y=x平移2个单位长度后,其顶点在直线y=x上的点A处,则平移后抛物线所对应的函数表达式是 .?
?
答案
9.y=(x-1)2+1 【解析】 把抛物线y=x2沿直线y=x平移2个单位长度,即将抛物线y=x2向上平移1个单位长度后再向右平移1个单位长度,所以平移后的抛物线所对应的表达式为y=(x-1)2+1.
?
10.[2020吉林长春一模]如图,在平面直角坐标系中,抛物线y=a(x+1)2+b与y=a(x-2)2+b+1交于点A.过点A作y轴的垂线,分别交两抛物线于点B,C(点B在点A左侧,点C在点A右侧),则线段BC的长为 .?
答案
10.6 【解析】 设抛物线y=a(x+1)2+b的对称轴与线段BC交于点E,抛物线y=a(x-2)2+b+1的对称轴与线段BC交于点F,如图所示.由抛物线的对称性,可知BE=AE,CF=AF,所以BC=BE+AE+AF+CF=2(AE+AF)=2×[2-(-1)]=6.
11.已知抛物线y=a(x+m)2的顶点坐标为(-1,0),且经过点A(-2,-12).
(1)求该抛物线对应的函数表达式;
(2)该抛物线是否经过点B(2,-2)?若不经过,怎样沿x轴方向平移,才能使它经过点B?并写出平移后的抛物线对应的函数表达式.
?
答案
11.【解析】 (1)∵抛物线y=a(x+m)2的顶点坐标为(-1,0),
∴m=1,
∵抛物线y=a(x+1)2经过点A(-2,-12),
∴a(-2+1)2=-12,解得a=-12,
∴该抛物线对应的函数表达式为y=-12(x+1)2.
?
答案
(2)不经过.
当x=2时,y=-12×(2+1)2=-92≠-2,
∴抛物线y=-12(x+1)2不经过点B(2,-2).
设平移后的抛物线对应的函数表达式为y=-12(x+1+n)2,
∵它经过点B(2,-2),∴-12(2+1+n)2=-2,
解得n=-1或n=-5,
∴将抛物线y=-12(x+1)2向右平移1个或5个单位长度,即可使它经过点B(2,-2),平移后的抛物线对应的函数表达式为y=
-12x2或y=-12(x-4)2.
?
12.如图,顶点为M的抛物线y=a(x+1)2-4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,-3).
(1)求抛物线的表达式;
(2)判断△BCM是否为直角三角形,并说明理由;
(3)在该抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
答案
12.【解析】 (1)∵抛物线y=a(x+1)2-4与y轴相交于点C(0,-3),∴-3=a(0+1)2-4,∴a=1.
∴抛物线的表达式为y=(x+1)2-4,即y=x2+2x-3.
(2)△BCM为直角三角形.理由如下:
解法一 将y=0代入y=x2+2x-3中,得
x2+2x-3=0,解得x1=-3,x2=1,
∴A(1,0),B(-3,0).∵C(0,-3),
∴OC=OB,∴∠OCB=45°.
如图1,过点M作MH⊥y轴于点H,由(1)知M(-1,-4),
则MH=CH=1,∴∠MCH=45°,
∴∠BCM=180°-∠OCB-∠MCH=90°,
∴△BCM为直角三角形.?
答案
解法二 将y=0代入y=x2+2x-3中,得x2+2x-3=0,
解得x1=-3,x2=1,
∴A(1,0),B(-3,0).
易得顶点M的坐标为(-1,-4).
在Rt△BOC中,由勾股定理得BC2=32+32=18,
∵C(0,-3),∴CM2=[(-3)-(-4)]2+12=2,
BM2=[(-1)-(-3)]2+42=20,
∴BC2+CM2=BM2,∴△BCM为直角三角形.
(3)存在.∵B(-3,0),C(0,-3),∴直线BC的表达式为y=-x-3.
在等腰直角三角形OBC中,OB=OC=3,
∴BC=32,同理可得CM=2.
由(2)可知,△BCM是直角三角形,∠BCM=90°,∴S△BCM=12×BC×CM=3.
?
答案
设点N的坐标为(t,t2+2t-3).
①当点N位于x轴的下方时,点N只能位于直线BC的下方.
如图2,过点N作ND∥y轴交BC于点D,连接BN,CN,
则D(t,-t-3),
∴DN=(-t-3)-(t2+2t-3)=-t2-3t.
∴S△BCN=S△BDN+S△CDN=-32t2-92t.
由已知得S△BCN=S△BCM,∴-32t2-92t=3,
解得t1=-2,t2=-1(舍去).
∴点N的坐标为(-2,-3).
②当点N位于x轴的上方时,
过点N作NE⊥x轴于点E,连接AN,BN,
则S△ABN=12×AB×NE=2t2+4t-6.
?
答案
由已知得S△ABN=S△BCM,∴2t2+4t-6=3,解得t=?2±222.
∴点N的坐标为(?2+222,32)或(?2?222,32).
综上所述,共存在3个满足条件的点N,它们的坐标分别为(-2,-3),(?2+222,32),(?2?222,32).
?
判断△BCM为直角三角形可通过证明三角形的一个内角是直角获得,也可通过勾股定理的逆定理获得.对于最后一问这种类型的题,当点的位置不确定时要分类讨论.
名师点睛
课时4 二次函数y=ax2+bx+c的图象与性质
课时4
1.将二次函数y=x2-4x+5化成y=a(x-h)2+k的形式为 ( )
A.y=(x-2)2+1 B.y=(x+2)2+1
C.y=(x-2)2+9 D.y=(x-4)2+1
答案
1.A 【解析】 y=x2-4x+5=x2-4x+4+1=(x-2)2+1.
知识点1 二次函数y=ax2+bx+c与y=a(x-h)2+k的关系
2.[2019山东济宁中考]将抛物线y=x2-6x+5向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线表达式是 ( )
A.y=(x-4)2-6 B.y=(x-1)2-3
C.y=(x-2)2-2 D.y=(x-4)2-2
答案
2.D 【解析】 y=x2-6x+5=(x-3)2-4,所以向上平移两个单位长度,再向右平移一个单位长度,平移后得到的抛物线表达式为y=(x-4)2-2.故选D.
知识点1 二次函数y=ax2+bx+c与y=a(x-h)2+k的关系
3.[2019重庆中考A卷]抛物线y=-3x2+6x+2的对称轴是 ( )
A.直线x=2 B.直线x=-2
C.直线x=1 D.直线x=-1
答案
3.C 【解析】 解法一 ∵y=-3x2+6x+2=-3(x-1)2+5,∴抛物线的对称轴为直线x=1.故选C.
解法二 ∵a=-3,b=6,c=2,∴抛物线y=-3x2+6x+2的图象的对称轴为直线x=-????2????=1.故选C.
?
知识点2 二次函数y=ax2+bx+c的图象与性质
4.[2020河北唐山期末]下列对二次函数y=2x2+x的描述,正确的是 ( )
A.图象开口向下
B.图象顶点坐标为(14,18)
C.图象经过原点
D.当x<0时,y随x值的增大而增大
?
答案
4.C 【解析】 ∵a=2,b=1,c=0,∴二次函数y=2x2+x的图象开口向上,顶点坐标为(-14,-18),故A,B项错误;二次函数y=2x2+x的图象的对称轴为直线x=-????2????=-14,当x<-14时,y随x值的增大而减小,当x>-14时,y随x值的增大而增大,故D项错误;当x=0时,y=2x2+x=0,∴二次函数y=2x2+x的图象经过原点,C项正确.故选C.
?
知识点2 二次函数y=ax2+bx+c的图象与性质
5.[2020湖北宜昌期中]二次函数y=ax2+bx+c的图象如图所示,若点A(-2.2,y1),B(-3.2,y2)是图象上的两点,则y1与y2的大小关系是 ( )?
A.y1C.y1>y2 D.不能确定
答案
5.A 【解析】 由题图,知该函数图象开口向下,对称轴是直线x=-3.因为点A(-2.2,y1),B(-3.2,y2)是图象上的两点,且点A到对称轴的距离大于点B到对称轴的距离,所以y1知识点2 二次函数y=ax2+bx+c的图象与性质
6.易错题若抛物线y=ax2-x+c与y=2(x-3)2+1的对称轴相同,且两抛物线的顶点相距3个单位长度,则c的值为 .?
答案
6.112或-12 【解析】 抛物线y=2(x-3)2+1的对称轴是直线x=3,顶点坐标为(3,1).∵抛物线y=ax2-x+c与y=2(x-3)2+1的对称轴相同,∴-?12????=3,解得a=16.∵两抛物线的顶点相距3个单位长度,∴抛物线y=16x2-x+c的顶点坐标为(3,4)或(3,-2).把(3,4)代入y=16x2-x+c,得c=112;把(3,-2)代入y=16x2-x+c,得c=-12.综上,c的值为112或-12.
?
知识点2 二次函数y=ax2+bx+c的图象与性质
7.[2019浙江宁波中考]如图,已知二次函数y=x2+ax+3的图象经过点P(-2,3).
(1)求a的值和图象的顶点坐标.
(2)点Q(m,n)在该二次函数图象上.
①当m=2时,求n的值;
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
知识点2 二次函数y=ax2+bx+c的图象与性质
答案
7.【解析】 (1)把点P(-2,3)代入y=x2+ax+3中,得a=2.
∴y=x2+2x+3=(x+1)2+2,
∴图象的顶点坐标为(-1,2).
(2)①把x=2代入y=x2+2x+3,得y=11.
∴当m=2时,n=11.
②n的取值范围为2≤n<11.
∵点Q到y轴的距离小于2,
∴|m|<2,∴-2∴2≤n<11.
知识点2 二次函数y=ax2+bx+c的图象与性质
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①a>0;②2a+b=0;③a+b+c>0;④当-10.其中正确的个数为 ( )
A.1 B.2 C.3 D.4
答案
8.C 【解析】 ∵图象的开口向下,∴a<0,故①错误;由题图知对称轴为直线x=?1+32=1,∴-????2????=1,∴2a+b=0,故②正确;∵当x=1时,对应的y值大于0,∴a+b+c>0,故③正确;∵当-10,故④正确.∴正确的结论有3个.故选C.
?
知识点3 二次函数y=ax2+bx+c的图象与a,b,c之间的关系
9.[2020甘肃四校联考]二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列四个结论:①ac<0;②4a+c<2b;③3b+2c<0;④当x>0时,y随x的增大而减小.其中正确的有 .(填序号)?
答案
9.①③④ 【解析】 ∵抛物线开口方向向下,∴a<0,∵抛物线与y轴正半轴相交,∴c>0,∴ac<0,①正确;∵x=0时,y>0,且对称轴为直线x=-1,∴当x=-2时,y>0,即4a-2b+c>0,∴4a+c>2b,②不正确;∵-????2????=-1,∴b=2a,当x=1时,y=a+b+c<0,
∴32b+c<0,∴3b+2c<0,③正确;由题中图象可知,当x>-1时,y随x的增大而减小,对于x>0时同样成立,④正确.故正确的有①③④.
?
知识点3 二次函数y=ax2+bx+c的图象与a,b,c之间的关系
1.如图,函数y=ax2-2x+1和y=ax-a(a是常数,且a≠0)在同一平面直角坐标系的图象可能是 ( )
答案
1.B 【解析】 抛物线y=ax2-2x+1过点(0,1),对称轴为直线x=1????.当a>0时,-a<0,1????>0,抛物线y=ax2-2x+1开口向上,对称轴在y轴右侧,直线y=ax-a经过第一、三、四象限,选项B符合题意,选项A,C不合题意;当a<0时,-a>0,1????<0,直线y=ax-a经过第一、二、四象限,抛物线y=ax2-2x+1开口向下,且对称轴在y轴左侧,选项D不符合题意.故选B.
?
2.已知二次函数y=ax2+(a+2)x-1(a为常数,且a≠0),则下列结论正确的是 ( )
A.若a>0,则当x<-1时,y随x的增大而增大
B.若a>0,则当x<-1时,y随x的增大而减小
C.若a<0,则当x<-1时,y随x的增大而增大
D.若a<0,则当x<-1时,y随x的增大而减小
答案
2.C 【解析】 ∵y=ax2+(a+2)x-1的对称轴为直线x=-????+22????=-12?1????.当a>0时,-1????<0,∴-12?1????<0,但大小无法确定,∴x<-1时,y随x增大的变化趋势无法判断;当a<0时,抛物线开口向下,-1????>0,∴-12?1????>-1,故当x<-1时,y随x的增大而增大.∴若a<0,则当x<-1时,y随x的增大而增大.故选C.
?
3.[2019山东烟台中考]已知二次函数y=ax2+bx+c的y与x的部分对应值如表:
给出下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当00;④抛物线与x轴的两个交点间的距离是4;⑤若A(x1,2),B(x2,3)是抛物线上两点,则x1A.2 B.3 C.4 D.5
答案
3.B 【解析】 因为x=0时,y=0,x=4时,y=0,所以抛物线的对称轴为直线x=2,故②正确.因为x=2时,y=-4,x=3时,y=-3>-4,对称轴为直线x=2,所以抛物线的开口向上,故①正确.由表格易知,③错误.抛物线与x轴的两个交点间的距离是4-0=4,故④正确.当A位于抛物线对称轴的右侧,B位于左侧时,x1>x2,故⑤错误.故选B.
x
-1
0
2
3
4
y
5
0
-4
-3
0
4.[2020河北唐山期末]已知二次函数y=x2-x+a(a>0),当自变量x取m时,其相应的函数值小于0,则下列结论正确的是 ( )
A.x取m-1时的函数值小于0
B.x取m-1时的函数值大于0
C.x取m-1时的函数值等于0
D.x取m-1时的函数值与0的大小关系不确定
答案
4.B 【解析】 由题意,画出函数y=x2-x+a(a>0)的大致图象如图所示.易知抛物线y=x2-x+a的对称轴为直线x=12.设抛物线与x轴交于点A,B,则A,B两点间的距离小于1,
∵x取m时,其相应的函数值小于0,∴观察图象可知,x=m-1在点A的左侧,∴当x=m-1时,y>0.故选B.
?
5.[2019湖北鄂州中考]二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.给出下列结论:①abc<0;②3a+c>0;
③(a+c)2-b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为 ( )?
A.1 B.2 C.3 D.4
答案
5.C 【解析】 ∵抛物线开口向上,∴a>0,∵抛物线的对称轴在y轴右侧,∴-????2????>0,∴b<0,∵抛物线与y轴交于负半轴,∴c<0,∴abc>0,①错误;当x=-1时,y>0,∴a-b+c>0,∵-????2????=1,∴b=-2a,把b=-2a代入a-b+c>0,得3a+c>0,②正确;当x=1时,y<0,∴a+b+c<0,又∵a-b+c>0,∴(a+b+c)(a-b+c)<0,∴(a+c)2-b2<0,③正确;∵抛物线的对称轴为直线x=1,∴x=1时,函数取得最小值,最小值为a+b+c,∴a+b+c≤am2+mb+c,a+b≤m(am+b),④正确.综上,②③④正确,共有3个.故选C.
?
6.[2020江苏无锡一模]已知抛物线y=-x2-2x+3,当-2≤x≤2时,对应的函数值y的取值范围为 .?
答案
6.-5≤y≤4 【解析】 y=-x2-2x+3=-(x+1)2+4,当x=-1时,二次函数有最大值4,当x=2时,y=-9+4=-5,∴-5≤y≤4.
7.[2020广东广州越秀区二段]如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,-2),且顶点在第三象限,设P=a-b+c,则P的取值范围是 .?
答案
7.-40.∵对称轴在y轴的左边,∴-????2????<0,∴b>0.∵图象与y轴的交点坐标是(0,-2),且过点(1,0),∴c=-2,a+b-2=0,∴b=2-a,∴P=a-b+c=2a-4,y=ax2+(2-a)x-2.把x=-1代入得,y=a-(2-a)-2=2a-4,∵b>0,
∴b=2-a>0,∴a<2.∵a>0,∴0?
8.[2020河北保定期中]如图,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上有一点D(m,n)(m>0,n>0),使S△ABD=S△ABC,求点D的坐标.
答案
8.【解析】 (1)将A(3,0)代入y=-x2+2x+m,
得-32+2×3+m=0,解得m=3.
(2)∵m=3,∴二次函数的表达式为y=-x2+2x+3.
令y=0,得-x2+2x+3=0,
解得x=3或x=-1.
∴点B的坐标为(-1,0).
(3)∵ S△ABD=S△ABC,点D在第一象限,
∴点C,D关于函数图象的对称轴对称.
∵点C为二次函数图象与y轴的交点,∴C(0,3),
又∵该二次函数图象的对称轴为直线x=-2?1×2=1,
∴点D的坐标为(2,3).
?
9.在平面直角坐标系中,抛物线y=2x2+mx+n经过点A(-1,a),B(3,a),且最低点的纵坐标为-4.
(1)求抛物线的函数表达式及a的值;
(2)设抛物线的顶点C关于y轴的对称点为点D,点P是抛物线对称轴上一动点,记抛物线在点A,B之间的部分为图象G(包含A,B两点).若直线DP与图象G恰有两个公共点,结合函数图象,求点P的纵坐标t的取值范围.
答案
9.【解析】 (1)∵抛物线y=2x2+mx+n经过点A(-1,a),B(3,a),∴抛物线的对称轴为直线x=1.
∵抛物线最低点的纵坐标为-4,
∴抛物线的顶点是(1,-4),
∴抛物线的函数表达式是y=2(x-1)2-4,
即y=2x2-4x-2.
把x=-1,y=a代入抛物线的函数表达式,解得a=4.?
(2)∵抛物线的顶点C(1,-4)关于y轴的对称点为点D,
∴D(-1,-4),
∴直线CD的函数表达式为y=-4,
由B(3,4),D(-1,-4),可得直线BD的函数表达式为y=2x-2,
当x=1时,y=0.
结合图象(如图所示),可得-43 确定二次函数的
表达式
课时1 已知图象上两点求二次函数的表达式
课时1
1.已知抛物线y=ax2+bx-2(a≠0)经过点A(-1,-2),B(1,0),则这个二次函数的表达式为 ( )
A.y=x2+x-2 B.y=-x2+x-2
C.y=x2-x-2 D.y=-x2-x-2
答案
1.A 【解析】 将点A(-1,-2),B(1,0)代入二次函数的表达式,得??????????2=?2,????+?????2=0,解得????=1,????=1,所以这个二次函数的表达式为y=x2+x-2.故选A.
?
知识点1 已知二次函数y=ax2+bx+c的某项系数或常数项求其表达式
2.二次函数y=x2+bx+c中,y与自变量x的部分对应值如表所示,则m的值为 .?
答案
2.-1 【解析】 由题意,得????=?1,1+????+????=?2,解得????=?2,????=?1,所以y=x2-2x-1,把x=2代入,得m=4-4-1=-1.
?
知识点1 已知二次函数y=ax2+bx+c的某项系数或常数项求其表达式
x
?
-2
-1
0
1
2
?
y
?
7
2
-1
-2
m
?
3.[2020河南南阳期末]已知二次函数y=ax2-3x+c的图象经过点(2,0)和(0,4).
(1)求该二次函数的表达式;
(2)画出该函数的图象.
知识点1 已知二次函数y=ax2+bx+c的某项系数或常数项求其表达式
答案
3.【解析】 (1)∵二次函数y=ax2-3x+c的图象经过点(2,0)和(0,4),
∴4?????6+????=0,????=4,解得????=12,????=4,
∴该二次函数的表达式为y=12x2-3x+4.
(2)图象如图所示:
?
知识点1 已知二次函数y=ax2+bx+c的某项系数或常数项求其表达式
4.[2020山东泰安期中]已知抛物线l与抛物线y=-3x2+2x-5的形状和开口方向均相同,且过点A(1,2),B(4,5).
(1)求抛物线l的表达式;
(2)用配方法求抛物线l的对称轴与顶点坐标.
答案
4.【解析】 (1)∵抛物线l与抛物线y=-3x2+2x-5的形状和开口方向均相同,
∴可设抛物线l的表达式为y=-3x2+bx+c,
∵抛物线l过点A(1,2),B(4,5),
∴?3+????+????=2,?3×42+4????+????=5,解得????=16,????=?11,
∴抛物线l的表达式为y=-3x2+16x-11.
(2)y=-3x2+16x-11=-3(x2-163x+649?649)-11=-3(x-83)2+313.
∴抛物线l的对称轴为x=83,顶点坐标为(83,313).
?
知识点1 已知二次函数y=ax2+bx+c的某项系数或常数项求其表达式
5.[2019甘肃庆阳期末]抛物线的顶点坐标为M(-2,1),且经过原点,则该抛物线对应的函数表达式为 ( )
A.y=(x-2)2+1 B.y=-14(x+2)2+1
C.y=(x+2)2+1 D.y=14(x+2)2+1
?
答案
5.B 【解析】 根据题意,设抛物线对应的函数表达式为y=a(x+2)2+1,将(0,0)代入,得4a+1=0,解得a=-14,所以y=-14(x+
2)2+1.故选B.
?
知识点2 用“顶点式”求二次函数的表达式
6.当x=1时,某二次函数取得最大值5,且该二次函数的图象与y轴交于点(0,2),则其表达式为 .?
答案
6.y=-3x2+6x+2 【解析】 由题意设该二次函数的表达式为y=a(x-1)2+5,∵该二次函数的图象与y轴交于点(0,2),∴将(0,2)代入函数表达式得2=a+5,∴a=-3,∴所求的二次函数的表达式为y=-3(x-1)2+5,即y=-3x2+6x+2.
知识点2 用“顶点式”求二次函数的表达式
7.已知抛物线的顶点坐标为(-2,3),开口方向与抛物线y=12x2相反,开口大小与抛物线y=13x2相同,则该抛物线对应的函数表达式为 .?
?
答案
7.y=-13x2-43x+53 【解析】 因为所求抛物线的顶点坐标为(-2,3),所以可设其对应的函数表达式为y=a(x+2)2+3,又因为所求抛物线开口方向与抛物线y=12x2相反,开口大小与抛物线y=13x2相同,所以a=-13,因此所求抛物线对应的函数表达式为y=-13(x+2)2+3=-13x2-43x+53.
?
知识点2 用“顶点式”求二次函数的表达式
8.已知二次函数图象的顶点坐标为(3,5),且抛物线经过点A(1,3).
(1)求此抛物线的表达式;
(2)如果点A关于抛物线的对称轴的对称点是点B,且抛物线与y轴的交点为点C,求△ABC的面积.
答案
8.【解析】 (1)由题意,可设抛物线的表达式为y=a(x-3)2+5,
将点A(1,3)代入,得4a+5=3,解得a=-12,
∴抛物线的表达式为y=-12(x-3)2+5.
(2)∵A(1,3),点A与点B关于对称轴x=3对称,
∴B(5,3),AB=4.
∵当x=0时,y=12,∴C(0,12),
∴S△ABC=12×4×(3-12)=5.
?
知识点2 用“顶点式”求二次函数的表达式
1.[2019河北沧州期末]已知二次函数的部分图象如图所示,对称轴是直线x=-1,则这个二次函数的表达式为 ( )?
A.y=-x2+2x+3 B.y=x2+2x+3
C.y=-x2+2x-3 D.y=-x2-2x+3
答案
1.D 【解析】 由题意知,抛物线的对称轴为直线x=-1,过点(-3,0),(0,3),设抛物线的表达式为y=a(x+1)2+k,将(-3,0),
(0,3)代入,得4????+????=0,????+????=3,解得????=?1,????=4,则抛物线的表达式为y=-(x+1)2+4=-x2-2x+3.故选D.
?
2.[2020浙江杭州拱墅区期末]已知二次函数y=x2+bx+c的图象经过点(2,4),且其顶点在直线y=2x+1上,则它的表达式为 ( )
A.y=x2-x+2 B.y=x2-x+3
C.y=x2-x+5 D.y=x2-2x+4
答案
2.D 【解析】 将(2,4)代入y=x2+bx+c,得4+2b+c=4,得c=-2b,所以二次函数的表达式为y=x2+bx-2b=(x+????2)2-????24-2b,顶点坐标为(-????2,-????24-2b),代入直线y=2x+1,得-b+1=-????24-2b,整理得b2+4b+4=0,解得b=-2,所以c=4,所以表达式为y=x2-2x+4.故选D.
?
3.已知二次函数y=ax2+bx+c的图象是由y=12x2的图象经过平移得到的,若图象与x轴交于点A,C(-1,0),与y轴交于点D(0,52),顶点为点B,则四边形ABCD的面积为 ( )
A.9 B.10 C.11 D.12
?
答案
3.A 【解析】 ∵y=ax2+bx+c的图象是由y=12x2的图象经过平移得到的,∴a=12,∴y=12x2+bx+c.
∵抛物线过点C(-1,0),D(0,52),∴12-b+c=0,c=52,∴b=3,∴ y=12x2+3x+52,∴-????2????=-3,4?????????????24????=-2,∴顶点B的坐标为(-3,-2).∵抛物线的对称轴为直线x=-3,C(-1,0),∴A点坐标为(-5,0),∴AC=4.如图,
S四边形ABCD=S△ACB+S△ACD=12×4×2+12×4×52=9.故选A.
?
4.已知抛物线y=ax2+bx+c经过点A(1,4),B(-2,1),且对称轴为直线x=-1,则当y随x的增大而增大时,x的取值范围为 .?
答案
4.x>-1 【解析】 根据题意,设y=a(x+1)2+k,将点A(1,4),B(-2,1)代入,得4????+????=4,????+????=1,解得????=1,????=0,所以抛物线的表达式为y=(x+1)2,可知当x>-1时,y随x的增大而增大.
?
5.易错题 [2020湖北武汉模拟]已知抛物线经过原点O,还经过点A(2,m),B(4,m).若△AOB的面积为4,则抛物线的表达式为 .?
答案
5.y=-12x2+3x或y=12x2-3x 【解析】 ∵抛物线经过点A(2,m),B(4,m),∴抛物线的对称轴是直线x=3,AB=2.∵△AOB的面积为4,∴12AB·|m|=4,∴m=±4.当m=4时,A(2,4),B(4,4).设抛物线的表达式为y=a(x-3)2+h,把(0,0)和(2,4)代入得9????+h=0,????+h=4,解得????=?12,h=92, ∴抛物线的表达式为y=-12(x-3)2+92,即y=-12x2+3x.当m=-4时,A(2,-4),B(4,-4),设抛物线的表达式为y=k(x-3)2+n,把(0,0)和(2,-4)代入得9????+????=0,????+????=?4,解得????=12,????=?92, ∴抛物线的表达式为y=12(x-3)2-92=12x2-3x.综上所述,抛物线的表达式为y=-12x2+3x或y=12x2-3x.
?
6.如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点E.
(1)求此抛物线对应的函数表达式;
(2)若直线y=x+1与该抛物线交于A,D两点,与y轴交于点F,连接DE,求△DEF的面积.
答案
6.【解析】 (1)∵抛物线y=x2+bx+c与x轴交于点 A(-1,0),B(3,0),
∴1?????+????=0,9+3????+????=0,解得????=?2,????=?3,
故此抛物线对应的函数表达式为y=x2-2x-3.
(2)由????=????+1,????=????2?2?????3,解得????1=?1,????1=0或????2=4,????2=5,
∴D(4,5).
对于直线y=x+1,令x=0,得y=1,∴F(0,1).
对于抛物线y=x2-2x-3,令x=0,得y=-3,
∴E(0,-3),∴EF=4,
∴S△DEF=12EF×4=12×4×4=8.
?
7.[2020江苏苏州期末]如图,在平面直角坐标系中,二次函数y=ax2+bx+6(a≠0)的图象经过点(4,6),与x轴交于A,B(6,0)两点,与y轴交于点C.
(1)求a,b的值;
(2)若点P为直线BC上一点,点P到A,B两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点P,求新抛物线的顶点坐标.
答案
7.【解析】 (1)∵二次函数y=ax2+bx+6(a≠0)的图象经过点(4,6),与x轴交于A,B(6,0)两点,
∴16????+4????+6=6,36????+6????+6=0,解得????=?12,????=2.
?
答案
(2)∵y=-12x2+2x+6=-12(x-2)2+8,
∴抛物线的对称轴为直线x=2,点C的坐标为(0,6).
∵点P到A,B两点的距离相等,
∴点P在抛物线的对称轴x=2上.
∵点B的坐标为(6,0),点C的坐标为(0,6),
∴直线BC的表达式为y=-x+6.
令x=2,则y=-2+6=4, ∴点P的坐标为(2,4).
设平移后的新抛物线的表达式为y=-12(x-h)2+8.
∵新抛物线经过点P,∴4=-12(2-h)2+8,
解得h1=2+22,h2=2-22,
∴新抛物线的顶点坐标为(2+22,8)或(2-22,8).
?
课时2 已知图象上三点求二次函数的表达式
课时2
1.已知二次函数的图象经过点(-1,-9),(1,-3)和(3,-5)三点,则该函数的表达式为( )
A.y=x2+3x-5 B.y=-x2+3x-5
C.y=x2-3x+5 D.y=-x2-3x+5
答案
1.B 【解析】 设二次函数的表达式为y=ax2+bx+c,则?????????+????=?9,????+????+????=?3,9????+3????+????=?5,解得????=?1,????=3,????=?5,所以此二次函数的表达式为y=-x2+3x-5.故选B.
?
知识点1 用“一般式”求二次函数的表达式
2.二次函数y=ax2+bx+c(a,b,c均为常数且a≠0)中的x与y的部分对应值如表所示:
给出下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小;③当x=2时,y=5;④x=3是方程ax2+(b-1)x+c=0的一个根.其中正确的有 .(填序号)?
答案
2.①③④ 【解析】 由x=0时y=3可知c=3,将(-1,-1),(1,5)代入,得?????????+3=?1,????+????+3=5,∴????=?1,????=3,∴二次函数的表达式为y=-x2+3x+3,ac=-3<0,①正确;∵y=-x2+3x+3=-(x-32)2+214,∴当x>32时,y的值随x值的增大而减小,②不正确;当x=2时,y=-4+
6+3=5,③正确;方程ax2+(b-1)x+c=0,即-x2+2x+3=0,解得x=-1或3,④正确.故正确的有①③④.
?
知识点1 用“一般式”求二次函数的表达式
x
?
-1
0
1
?
y
?
-1
3
5
?
3.有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴是y轴.
乙:与x轴有两个交点,其中一个交点的横坐标为1.
丙:与y轴交点的纵坐标是个正数,且以与坐标轴的三个交点为顶点的三角形面积为3.
请写出满足上述全部特点的二次函数的表达式为 .?
答案
3.y=-3x2+3 【解析】 设该二次函数的表达式为y=ax2+bx+c.∵抛物线的对称轴是y轴,∴该二次函数的表达式为y=ax2+c.∵该二次函数的图象与x轴有两个交点,其中一个交点的横坐标为1,∴a+c=0,另一个交点的横坐标为-1.∵该二次函数与y轴交点的纵坐标是个正数,且以三个交点为顶点的三角形面积为3,∴c>0,12×[1-(-1)]×c=3,解得c=3,∴a=
-3.∴满足甲、乙、丙三位同学说的全部特点的二次函数的表达式为y=-3x2+3.
?
知识点1 用“一般式”求二次函数的表达式
4.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表所示.
(1)求该二次函数的表达式;
(2)当x为何值时,y有最小值?最小值是多少?
(3)若点A(m,y1),B(m+1,y2)都在该函数的图象上,试比较y1与y2的大小.
知识点1 用“一般式”求二次函数的表达式
x
?
-1
0
1
2
?
y
?
10
5
2
1
?
答案
4.【解析】 (1)由题表中数据,知当x=-1时,y=10;当x=0时,y=5;当x=1时,y=2.
∴?????????+????=10,????=5,????+????+????=2,解得????=1,????=?4,????=5,
∴该二次函数的表达式为y=x2-4x+5.
(2)由(1)知y=x2-4x+5=(x-2)2+1,
∴当x=2时,y有最小值,最小值是1.
(3)∵点A(m,y1),B(m+1,y2)都在函数y=x2-4x+5的图象上,
∴y1=m2-4m+5,y2=(m+1)2-4(m+1)+5=m2-2m+2,
∴y2-y1=(m2-2m+2)-(m2-4m+5)=2m-3,
∴①当2m-3<0,即m<32时,y1>y2;
②当2m-3=0,即m=32时,y1=y2;
③当2m-3>0,即m>32时,y1?
知识点1 用“一般式”求二次函数的表达式
5.已知二次函数的图象如图所示,则该二次函数的表达式为 ( )
A.y=13x2+23x+1
B.y=13x2+23x-1
C.y=13x2-23x+1
D.y=13x2-23x-1
?
答案
5.D 【解析】 设抛物线的表达式为y=a(x+1)(x-3),将点(0,-1)代入,得-3a=-1,解得a=13,所以y=13(x+1)(x-3)=13x2-23x-1.故选D.
?
知识点2 用“交点式”求二次函数的表达式
6.易错题 已知抛物线过点A(-1,0)和点B(3,0),与y轴交于点C,且BC=32,则这条抛物线的表达式为 ( )
A.y=-x2+2x+3
B.y=x2-2x-3
C.y=-x2+2x+3或y=x2-2x-3
D.y=x2+2x-3或y=-x2+2x+3
?
答案
6.C 【解析】 设原点为O,因为BC=32,OB=3,所以点C的坐标有两种可能:C1(0,3),C2(0,-3).设所求抛物线的表达式为y=a(x+1)(x-3),将C1(0,3)代入,得a=-1;将C2(0,-3)代入,得a=1.所以所求抛物线的表达式为y=-x2+2x+3或y=x2-2x-3.故选C.
?
知识点2 用“交点式”求二次函数的表达式
7.已知抛物线y=ax2+bx+c的开口大小与开口方向均与抛物线y=-3x2+1相同,且与x轴相交于点(-2,0),(1,0),则该抛物线的表达式为 . ?
答案
7.y=-3x2-3x+6 【解析】 由题意可得a=-3.因为抛物线与x轴相交于点(-2,0),(1,0),所以抛物线的表达式为y=-3(x+
2)(x-1)=-3x2-3x+6.
知识点2 用“交点式”求二次函数的表达式
8.已知二次函数的图象与x轴的交点为(-5,0),(2,0),且经过点(3,-4),求此二次函数的表达式.
答案
8.【解析】 因为二次函数的图象与x轴的交点为(-5,0),(2,0),
所以设二次函数的表达式为y=a(x+5)(x-2),
又因为图象经过点(3,-4),
所以-4=a×8×1,解得a=-12.
所以此二次函数的表达式为y=-12(x+5)(x-2),
即y=-12x2-32x+5.
?
知识点2 用“交点式”求二次函数的表达式
9.如图,在平面直角坐标系中,已知直线y=-12x+4与y轴交于点A,与x轴交于点B,点C的坐标为(-2,0).
(1)求经过A,B,C三点的抛物线的表达式;
(2)如果M为抛物线的顶点,连接AM,BM,求四边形AOBM的面积.
?
知识点2 用“交点式”求二次函数的表达式
答案
9.【解析】 (1)对于y=-12x+4,当x=0时,y=4,∴A(0,4).
当y=0时,-12x+4=0,解得x=8,∴B(8,0).
设抛物线的表达式为y=a(x+2)(x-8),
将点A(0,4)代入,得-16a=4,解得a=-14,
∴y=-14(x+2)(x-8)=-14x2+32x+4.
(2)∵y=-14x2+32x+4=-14(x-3)2+254,∴M(3,254).
如图,过点M作MD⊥x轴于点D,则MD=254,OD=3,
∴S四边形AOBM=S梯形AODM+S△BDM=12×(4+254)×3+12×(8-3)×254=31.
?
知识点2 用“交点式”求二次函数的表达式
专项3 二次函数的存在性
问题
1.[2020山东潍坊一模]如图,抛物线y=ax2+bx+c与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的函数表达式.
(2)直线BC上方的抛物线上是否存在一点F,使四边形ABFC的面积为17?若存在,求出点F的坐标;若不存在,请说明理由.
答案
1.【解析】 (1)∵A(-2,0)与点B关于对称轴x=1对称,∴B(4,0).
设抛物线的函数表达式为y=a(x+2)(x-4),
∵C(0,4)在y=a(x+2)(x-4)的图象上,
∴4=a×2×(-4),∴a=-12,
∴y=-12(x+2)(x-4)=-12(x2-2x-8)=-12x2+x+4.
?
答案
(2)不存在.理由如下:
假设存在满足条件的点F,如图,连接OF.
∵A(-2,0),B(4,0),C(0,4),∴OA=2,OC=4,OB=4.
设点F(t,-12t2+t+4),其中0∴S四边形ABFC=S△OCF+S△OBF+S△AOC=12×4t+12×4(-12t2+t+4)+12×4×2=-t2+4t+12.
若-t2+4t+12=17,则t2-4t=-5,
∴t2-4t+4=-5+4,∴(t-2)2=-1<0,
∴方程-t2+4t+12=17无解.
故不存在满足条件的点F.
?
2.如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C.
(1)求该抛物线的表达式.
(2)在y轴上是否存在一点P,使△PBO与△AOC相似?若存在,写出点P的坐标;若不存在,请说明理由.
(3)在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
答案
2.【解析】 (1)将点A(1,0),B(-3,0)代入抛物线y=-x2+bx+c,得?1+????+????=0,?9?3????+????=0,解得????=?2,????=3,
∴该抛物线的表达式为y=-x2-2x+3.
(2)存在.
当x=0时,y=3,∴C(0,3),
∴AO=1,BO=3,CO=3.
∵点P在y轴上,∴∠BOP=∠AOC=90°,
∴△PBO与△AOC相似分两种情况.
①当△POB∽△COA时,????????????????=????????????????,
解得PO=9,
∴点P的坐标为(0,9)或(0,-9).
?
答案
②当△POB∽△AOC时,????????????????=????????????????,
解得PO=1,
∴点P的坐标为(0,1)或(0,-1).
∴满足题意的点P的坐标为(0,1),(0,-1),(0,9),(0,-9).
(3)存在.
由题知A,B两点关于抛物线的对称轴x=-1对称,
∴直线BC与x=-1的交点即所求点Q,此时△AQC周长最小.
设直线BC的表达式为y=mx+n,
∴?3????+????=0,????=3,解得????=1,????=3,
∴直线BC的表达式为y=x+3,
当x=-1时,y=2,
∴Q(-1,2).
?
3.[2020广西钦州三模]如图是将抛物线y=-x2平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C.
(1)求该抛物线的函数表达式;
(2)若点N为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=32x+32的图象上一点,若四边形OAPQ为平行四边形,这样的点P,Q是否存在?若存在,分别求出点P,Q的坐标;若不存在,说明理由.
?
答案
3.【解析】 (1)设抛物线的函数表达式是y=-(x-1)2+k.
把A(-1,0)代入,得0=-(-1-1)2+k,解得k=4,
∴抛物线的函数表达式是y=-(x-1)2+4,即y=-x2+2x+3.
(2)在y=-x2+2x+3中,令x=0,则y=3,
∴点C的坐标是(0,3),OC=3.
易知点B的坐标是(3,0),∴OB=3,
∴OC=OB,则△OBC是等腰直角三角形,∴∠OCB=45°.
由题意知,点N在y轴的右侧.如图,过点N作NH⊥y轴,垂足为点H.
∵∠NCB=90°,∴∠NCH=45°,∴NH=CH,
∴HO=OC+CH=3+CH=3+NH.
设点N的坐标是(a,-a2+2a+3),
∴a+3=-a2+2a+3,解得a=0(舍去)或a=1,
∴-a2+2a+3=4,
∴点N的坐标是(1,4).
答案
(3)存在.
如图,∵四边形OAPQ是平行四边形,∴PQ=OA=1,且PQ∥OA,
设P(t,-t2+2t+3),则Q(t+1,-t2+2t+3),
将Q(t+1,-t2+2t+3)代入y=32x+32,得-t2+2t+3=32(t+1)+32,
解得t=0或t=12,∴-t2+2t+3的值为3或154,
∴存在这样的点P,Q,且点P,Q的坐标分别是(0,3),(1,3)或(12,154),(32,154).
?
4.[2019江苏盐城中考]如图所示,二次函数y=k(x-1)2+2的图象与一次函数y=kx-k+2的图象交于A,B两点,点B在点A的右侧,直线AB分别与x轴,y轴交于C,D两点,其中k<0.
(1)求A,B两点的横坐标;
(2)若△OAB是以OA为腰的等腰三角形,求k的值;
(3)二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.
答案
4.【解析】 (1)联立两函数的表达式为????=????(?????1)2+2,????=?????????????+2,
解得????=1,????=2或????=2,????=????+2.
∵点B在点A的右侧,
∴点A,B的横坐标分别为1,2.
(2)由(1)知点A的坐标为(1,2),点B的坐标为(2,k+2),
故OA2=12+22=5,OB2=22+(k+2)2=k2+4k+8,AB2=(2-1)2+(2-k-2)2=k2+1.
①当OA=OB时,k2+4k+8=5,
解得k1=-1,k2=-3.
②当OA=AB时,k2+1=5,
解得k3=-2,k4=2(不符合题意,舍去),
综上所述,k的值为-1,-2或-3.
?
答案
(3)存在,k的值为-3或?4?73.
解法一 ①当点B在x轴上方时,k+2>0,即-2如图1,过点B作BF⊥AE于点F,在AF上找一点G,使∠GBF=∠FBE,则GF=EF.
∵BF⊥AE,AE⊥x轴,
∴BF∥x轴,
∴∠FBE=∠BEC.
∵∠GBF=∠FBE,
∴∠GBE=∠GBF+∠FBE=2∠BEC.
∵AE∥y轴,
∴∠BAE=∠ODC.
∵∠ODC=2∠BEC,
∴∠BAE=2∠BEC,
∴∠BAE=∠GBE.
?
答案
又∵∠GEB=∠BEA,
∴△EBG∽△EAB,
∴????????????????=????????????????,即EB2=EG·EA.
∵A(1,2),B(2,k+2),
∴E(1,0),F(1,k+2).
∵GE=2EF=2k+4,BE2=12+(k+2)2=k2+4k+5,EA=2,
∴k2+4k+5=2×(2k+4),解得k1=-3,k2=3(不符合题意,舍去).
②当点B在x轴下方时,k+2<0,即k<-2.
如图2,过点B作BM⊥直线AE于点M,在线段AM的延长线上找一点N,使∠NBM=∠EBM,则EM=MN.
同①易证△BNE∽△ANB,
∴????????????????=????????????????,即BN2=EN·NA.
?
答案
∵A(1,2),B(2,k+2),
∴E(1,0),M(1,k+2),
∴NE=2EM=-2k-4,BN2=BE2=12+(k+2)2=k2+4k+5,NA=2-(2k+4)=-2k-2,
∴k2+4k+5=(-2k-4)(-2k-2),
解得k3=?4?73,k4=?4+73(不符合题意,舍去),
综上所述,存在实数k,使得∠ODC=2∠BEC,k的值为-3或?4?73.
解法二 由题意得点E的坐标为(1,0).
对于一次函数y=kx-k+2,当y=0时,x=?????2????,即点C的坐标为(?????2????,0).
当x=0时,y=-k+2,即点D的坐标为(0,-k+2),
∴tan∠ODC=????????????????=?????2?????????+2=-1????.
过点B作BP⊥x轴,垂足为P,则EP=2-1=1,BP=|k+2|,
在线段EP上找一点Q,使得QE=QB,则∠BQP=2∠BEC,
?
答案
设QE=QB=m,则PQ=1-m.
在Rt△BQP中,BP2+QP2=BQ2,
∴(k+2)2+(1-m)2=m2,
整理,得2m=k2+4k+5.
∵∠ODC=2∠BEC,
∴tan∠BQP=tan∠ODC=-1????,
∴????????????????=|????+2|1?????=-1????.
①当k+2>0,即-2????+21?????=-1????,解得k1=-3,k2=3(不符合题意,舍去).
②当k+2<0,即k<-2时,
??????21?????=-1????,解得k3=?4?73,k4=?4+73(不符合题意,舍去).
综上所述,存在实数k,使得∠ODC=2∠BEC,k的值为-3或?4?73.
?
易错疑难集训(一)
集训(一)
1.[2020河南洛阳期末]已知二次函数y=mx2+x+m(m-2)的图象经过原点,则m的值为( )
A.0或2 B.0
C.2 D.无法确定
答案
1.C 【解析】 根据题意,得m(m-2)=0,∴m=0或m=2,∵二次函数的二次项系数不为0,∴m=2.故选C.
易错点1 忽略“二次项系数不为0”
2.已知函数y=(1-n)????????2+?????4是关于x的二次函数,当n为何值时,抛物线有最低点?求出这个最低点的坐标,在这种情况下,x为何值时,函数y随x的增大而增大?
?
答案
2.【解析】 因为函数y=(1-n)????????2+?????4是二次函数,
所以????2+?????4=2,1?????≠0,解得n=2或n=-3.
又因为抛物线有最低点,所以1-n>0,解得n<1,所以n=-3.
此时y=4x2,
所以当n=-3时,抛物线有最低点,这个最低点的坐标是(0,0),
在这种情况下,当x>0时,函数y随x的增大而增大.
?
易错点1 忽略“二次项系数不为0”
抛物线有最低点或最高点,是由二次函数y=ax2+bx+c的二次项系数a的符号决定的.当a>0时,抛物线有最低点;当a<0时,抛物线有最高点.本题易误认为当1-n<0时,抛物线有最低点,错误得出n=2.也易误认为当x<0时,函数y随x的增大而增大.
易错点1 忽略“二次项系数不为0”
3.将函数y=x2+x的图象向右平移a(a>0)个单位长度,得到函数y=x2-3x+2的图象,则a的值为 ( )
A.1 B.2
C.3 D.4
答案
3.B 【解析】 将函数y=x2+x的图象向右平移a(a>0)个单位长度,根据二次函数图象的平移规律可得,y=(x-a)2+(x-a),整理得y=x2-(2a-1)x+a2-a,而平移后的函数为y=x2-3x+2,可知-(2a-1)=-3,a2-a=2,所以a=2.故选B.
易错点2 对二次函数图象的平移规则理解不透
4.若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先向右平移1个单位长度,再向上平移3个单位长度,则得到的抛物线的表达式为 ( )
A.y=(x-2)2+3 B.y=(x-2)2+5
C.y=x2-1 D.y=x2+4
答案
4.C 【解析】 将平面直角坐标系xOy先向右平移1个单位长度,再向上平移3个单位长度,相当于把抛物线向左平移1个单位长度,再向下平移3个单位长度.∵y= x2-2x+3=(x-1)2+2,∴得到的抛物线的表达式为y=(x-1+1)2+2-3=x2-1.故选C.
易错点2 对二次函数图象的平移规则理解不透
5.把抛物线y=ax2+bx+c先向右平移3个单位长度,再向下平移2个单位长度,所得的图象的表达式是y=x2-3x+5,则a+b+c= .?
答案
5.11 【解析】 利用逆向思维来解题.因为将抛物线y=ax2+bx+c先向右平移3个单位长度,再向下平移2个单位长度后,得到抛物线y=x2-3x+5,所以将抛物线y=x2-3x+5先向左平移3个单位长度,再向上平移2个单位长度后,可得抛物线y=ax2+
bx+c,所以y=(x+3)2-3(x+3)+5+2=x2+3x+7=ax2+bx+c,令x=1,则a+b+c=11.
易错点2 对二次函数图象的平移规则理解不透
1.当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为 .?
答案
1.2或-3 【解析】 易知二次函数y=-(x-m)2+m2+1的图象的对称轴为直线x=m.①若m<-2,则当x=-2时,y有最大值-4m-3,令-4m-3=4,解得m=-74,与m<-2矛盾,故m值不存在;②若-2≤m≤1,则当x=m时,y有最大值m2+1,令m2+1=4,解得m1=-3,m2=
3(舍去);③若m>1,则当x=1时,y有最大值2m,令2m=4,解得m=2.综上所述,m的值为2或-3.
?
疑难点1 二次函数在自变量范围内的最值问题
本题考查二次函数的最值问题,难点在于分情况讨论.根据对称轴的位置,分三种情况讨论求解即可.
2.如图,一段抛物线y=-x2+4(-2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1,将C1绕点A1旋转180°得到C2,顶点为D2.C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是 ( )?
A.6C.10答案
2.D 【解析】 翻折后的抛物线的表达式为y=(x-4)2-4=x2-8x+12.∵x1,x2,x3均为正数,∴由题图知,点P1(x1,y1),P2(x2,y2),
P3(x3,y3)在第四象限,∴2≤x3≤4,根据抛物线的对称性可知x1+x2=8,∴10≤x1+x2+x3≤12,即10≤t≤12.故选D.
疑难点2 抛物线的全等变换问题
3.[2020江苏南京期末]已知二次函数y=ax2+bx+c(a≠0),y与自变量x的部分对应值如表所示:
则该二次函数图象关于x轴对称的图象所对应的函数表达式为 .?
答案
3.y=-x2+2x+3 【解析】 解法一 根据题意,知原二次函数图象的顶点坐标为(1,-4),设原二次函数的表达式为y=a(x-1)2-4,把(0,-3)代入y=a(x-1)2-4,得-3=a(0-1)2-4, 解得a=1,所以原二次函数的表达式y=(x-1)2-4.因为原二次函数图象的顶点坐标为(1,-4),所以该点关于x轴对称的点的坐标是(1,4),所以该二次函数图象关于x轴对称的图象所对应的函数表达式是y=-(x-1)2+4=-x2+2x+3.
解法二 根据题意,知原二次函数图象的顶点坐标为(1,-4),该点关于x轴对称的点的坐标是(1,4),设新二次函数的表达式为y=a(x-1)2+4,(0,-3)关于x轴对称的点的坐标是(0,3),把(0,3)代入y=a(x-1)2+4,得3=a(0-1)2+4, 解得a=-1,所以该二次函数图象关于x轴对称的图象所对应的函数表达式是y=-(x-1)2+4=-x2+2x+3.
疑难点2 抛物线的全等变换问题
x
?
-2
-1
0
1
2
?
y
?
5
0
-3
-4
-3
?
4.[2020湖北襄阳樊城区模拟]如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点.动点P在线段OA上,从点O出发,向点A以1个单位长度/s的速度匀速运动;同时,动点Q在线段AB上,从点A出发,向点B以2个单位长度/s的速度匀速运动.连接PQ,设运动时间为t s.
(1)求抛物线的表达式;
(2)当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E;过点Q作QF∥y轴,交抛物线于点F,连接EF.当EF∥PQ时,求点F的坐标.
?
疑难点3 二次函数与动点问题的综合
答案
4.【解析】 (1)由题可知,A(3,0),B(0,3),
将A(3,0),B(0,3)代入y=-x2+bx+c,得
?9+3????+????=0,????=3,解得????=2,????=3,
∴抛物线的表达式为y=-x2+2x+3.
(2)∵OA=OB=3,OA⊥OB,∴∠PAQ=45°.
当运动时间为t s时,AQ=2t,OP=t,AP=3-t.
①当∠AQP=90°时,在Rt△APQ中,cos∠PAQ=????????????????=22,
∴2????3?????=22,解得t=1;
②当∠APQ=90°时,在Rt△APQ中,cos∠PAQ=????????????????=22,
?
疑难点3 二次函数与动点问题的综合
答案
∴3?????2????=22,解得t=32.
综上所述,当t=1或32时,△APQ为直角三角形.
(3)如图,过点Q作QH⊥x轴于点H,
由题意知点P的坐标为(t,0),
则点E的坐标为(t,3-t),EP=3-t.
∵AQ=2t,∴AH=AQcos∠PAQ=t,∴OH=3-t.
将x=3-t代入y=-x+3中,得y=t,∴Q(3-t,t),
将x=3-t代入y=-x2+2x+3中,得y=-(3-t)2+2(3-t)+3=-t2+4t,∴F(3-t,-t2+4t),
∴QF=-t2+4t-t=-t2+3t,
∵PE∥y轴,QF∥y轴,∴PE∥QF,
?
疑难点3 二次函数与动点问题的综合
答案
又∵EF ∥ PQ,∴四边形PQFE是平行四边形,
∴EP=QF,∴3-t=-t2+3t,
解得t1=1,t2=3(舍去),
∴点F的坐标为(2,3).
疑难点3 二次函数与动点问题的综合
4 二次函数的应用
课时1 利用二次函数解决面积最值问题
课时1
1.用一条长为40 cm的绳子围成一个面积为 S cm2 的矩形,则S的值不可能为 ( )
A.20 B.40 C.100 D.120
答案
1.D 【解析】 设所围成矩形的一边长为x cm,则由题意,得S=x(20-x)=-x2+20x,∵-1<0,∴S有最大值,即当 x=-202×(?1)=
10时,S最大=100.∵120>100,∴S的值不可能为120.故选D.
?
知识点 利用二次函数解决面积最值问题
2.如图,在矩形ABCD中,AD=4,点E在边AD上,不与A,D重合,连接CE,以CE为边向右上方作正方形CEFG,过点F作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED.
(2)当AE为何值时,△AEF的面积最大?
知识点 利用二次函数解决面积最值问题
答案
2.【解析】 (1)∵四边形CEFG是正方形,∴CE=EF.
∵∠FEC=∠FEH+∠CED=90°,∠DCE+∠CED=90°,
∴∠FEH=∠DCE.
∵∠FHE=∠D=90°,∴△FEH≌△ECD,
∴FH=ED.
(2)设AE=a(0∴S△AEF=12AE·FH=12a(4-a)=-12(a-2)2+2,
∴当AE=2时,△AEF的面积最大.
?
知识点 利用二次函数解决面积最值问题
3.如图,在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A出发沿AB边向点B以1 cm/s的速度运动,同时点Q从点B出发沿BC边向点C以2 cm/s的速度运动,当其中一点运动至终点时,另一点也随之停止运动.
(1)设运动t s后,五边形APQCD的面积为S cm2,写出S与t之间的函数关系式,并指出自变量t的取值范围.
(2)t为何值时,S最小?最小值是多少?
知识点 利用二次函数解决面积最值问题
答案
3.【解析】 (1)t s时,AP=tcm,BQ=2t cm,
故PB=(6-t)cm,
故S△PBQ=12(6-t)·2t=(-t2+6t)(cm2).
∵S矩形ABCD=6×12=72(cm2),
∴S=72-S△PBQ=t2-6t+72.
自变量t的取值范围为0(2)由(1)知S=(t-3)2+63.
故当t=3时,S最小,最小值是63.
?
知识点 利用二次函数解决面积最值问题
4.如图,在一面靠墙的空地上,用长24 m的篱笆围成中间隔有两道篱笆的长方形花圃,墙的最大可用长度为8 m,设花圃的一边AB的长为x m,面积为S m2.
(1)求S与x之间的函数关系式.
(2)求自变量x的取值范围.
(3)当x取何值时,所围成的花圃面积最大?最大面积是多少?
知识点 利用二次函数解决面积最值问题
答案
4.【解析】 (1)花圃的一边AB长为x m,则BC长为(24-4x)m,
根据题意,得S与x之间的函数关系式为S=x(24-4x)=-4x2+24x.
(2)∵墙的最大可用长度为8 m,
∴0<24-4x≤8,解得4≤x<6,
即自变量x的取值范围为4≤x<6.
(3)由(1)知S=-4x2+24x=-4(x-3)2+36,
∴当x>3时,S的值随x值的增大而减小.
∵4≤x<6,
∴当x=4时,S取得最大值,且最大值为32,
∴当x取4时,花圃面积最大,最大面积是32 m2.
知识点 利用二次函数解决面积最值问题
5.[2020江苏连云港期末]为了节省材料,某水产养殖户利用水库堤岸(堤岸足够长)为一边,用总长为80 m的围网在水库中围成如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长为x m,矩形区域ABCD的面积为
y m2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围.
(2)x为何值时,y有最大值?最大值是多少?
知识点 利用二次函数解决面积最值问题
答案
5.【解析】 (1)解法一 设AE=a m,
由题意,得AE·AD=2BE·BC,AD=BC,
所以BE=12am,AB=32a m.
由题意,得2x+3a+a=80,
所以a=20-12x,y=AB·BC=32a·x=32(20-12x)x,
即y=-34x2+30x,其中0解法二 根据题意,得CF·x=13y,CF=????3????,
DF·x=23y,DF=2????3????,
所以2x+2×????3????+3×2????3????=80,
整理,得y=-34x2+30x,其中0?
知识点 利用二次函数解决面积最值问题
答案
(2)由(1)知y=-34x2+30x=-34(x-20)2+300,
因为-34<0,所以抛物线开口向下,
又因为0?
知识点 利用二次函数解决面积最值问题
1.[2019浙江绍兴柯桥区期末]在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x.若在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为 ( )
A.193 m2 B.194 m2 C.195 m2 D.196 m2
答案
1.C 【解析】 ∵AB=xm,∴BC=(28-x)m,则S=AB·BC=x(28-x)=-x2+28x.由题意可知????≥6,28?????≥15,解得6≤x≤13.易知当6≤x≤13时,S随x的增大而增大,∴当x=13时,S取得最大值,最大值为195 m2.故选C.
?
2.如图,在△ABC中,∠B=90°,AB=12 cm,BC=24 cm,动点P从点A开始沿边AB向点B以2 cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向点C以4 cm/s的速度移动(不与点C重合).若P,Q分别从A,B同时出发,则经过 s,四边形APQC的面积最小.?
答案
2.3 【解析】 设运动时间为t s,易知012×12×24-12(12-2t)×4t=(4t2-24t+144)(cm2),根据二次函数的图象和性质,知当t=-?242×4=3时,四边形APQC的面积最小.
?
3.如图,在直角三角形AEF内部作矩形ABCD,其中AB和AD分别在两直角边上,点C在斜边上,设矩形的一边AB长为x,矩形的面积为y,则y的最大值为 .?
答案
3.300 【解析】 由题可知,△EDC∽△EAF,CD=AB=x,∴????????????????=????????????????,∴30?????????30=????40,解得AD=30-34x,∴y=AD·AB=(30-34x)·x,即y=-34(x-20)2+300,∴当x=20时,y取得最大值300.
?
4.[2020河北石家庄新华区一模]如图,西游乐园景区内有一块矩形油菜花田地(单位:m),现在其中修建一条观花道(阴影所示),供游人赏花,设修建的观花道的面积为y m2.
(1)求y与x之间的函数关系式;
(2)若修建的观花道的面积为13 m2,求x的值;
(3)若要求0.6≤x≤1,求修建后油菜花地所占面积的最大值.
答案
4.【解析】 (1)y=6×8-2×12×(6-x)(8-x)=-x2+14x(0(2)当y=13时,-x2+14x=13,解得x=1或x=13.
∵0(3)设修建后油菜花地占地面积为w m2,
则w=48-y=x2-14x+48=(x-7)2-1,
∴当x<7时,w随x的增大而减小,
又∵0.6≤x≤1,
∴当x=0.6时,w取得最大值,最大值为39.96.
答:修建后油菜花地所占面积的最大值为39.96 m2.
?
5.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3).
(1)求抛物线的函数表达式及顶点D的坐标;
(2)若P为线段BD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAC面积的最大值和此时点P的坐标.
答案
5.【解析】 (1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3),代入y=ax2+bx+c,
得????=3,?????????+????=0,9????+3????+????=0,解得????=?1,????=2,????=3,
∴抛物线的函数表达式为y=-x2+2x+3,
∴抛物线的顶点D的坐标为(1,4).
(2)设直线BD的函数表达式为y=kx+m,
由B(3,0),D(1,4)得3????+????=0,????+????=4,解得????=?2,????=6,
∴直线BD的函数表达式为y=-2x+6.
∵点P在线段BD上,∴设P(p,-2p+6)(1≤p<3),
则OM=p,PM=-2p+6,
又∵OA=1,OC=3,
?
答案
∴四边形PMAC的面积为12×1×3+12×(-2p+6+3)×p=-p2+92p+32=-( p-94)2+10516.
∵1<94<3,
∴当p=94时,四边形PMAC的面积有最大值,最大值为10516,
此时,-2p+6=-2×94+6=32,点P的坐标为(94,32).
?
6.[2019浙江绍兴中考]有一块形状如图所示的五边形余料ABCDE,AB=AE=6,BC=5,∠A=∠B=90°,∠C=135°,∠E>90°.要在这块余料中截取一块矩形材料,其中一条边在AE上,并使所截矩形材料的面积尽可能大.
(1)若所截矩形材料的一条边是BC或AE,求矩形材料的面积.
(2)能否截出比(1)中更大面积的矩形材料?如果能,求出能截取矩形材料面积的最大值;如果不能,说明理由.
答案
6.【解析】 (1)设矩形材料的面积为S.
①若所截矩形材料的一条边是BC,如图1所示.
过点C作CF⊥AE于F,S=AB·BC=6×5=30.
②若所截矩形材料的一条边是AE,如图2所示.
过点E作EF∥AB交CD于F,过点F作FG⊥AB于G,过点C作CH⊥FG于H,
则四边形AEFG为矩形,四边形BCHG为矩形,
∴AE=FG=6,HG=BC=5.
∵∠BCD=135°,∴∠FCH=45°,
∴△CHF为等腰直角三角形,
∴BG=CH=FH=FG-HG=6-5=1,
∴AG=AB-BG=6-1=5,
∴S=AE·AG=6×5=30.
答案
(2)能.
如图3,在CD上取点F,过点F作FM⊥AB于M,FN⊥AE于N,过点C作CG⊥FM于G,
则四边形ANFM为矩形,四边形BCGM为矩形,
∴MG=BC=5,BM=CG.
∵∠BCD=135°,∴∠FCG=45°,
∴△CGF为等腰直角三角形,FG=CG.
设AM=x(0∴FM=GM+FG=GM+CG=BC+BM=11-x,
∴S=AM×FM=x(11-x)=-x2+11x=-(x-5.5)2+30.25,
∴当x=5.5时,S取得最大值,最大值为30.25.
课时2 利用二次函数解决利润最大问题
课时2
1.某鞋帽专卖店销售一种绒帽,若销售这种帽子每天的利润y(元)与销售价格x(元/件)满足关系式y=-x2+70x-800,想要获得最大利润,则销售价格为 ( )
A.30元/件 B.35元/件
C.40元/件 D.45元/件
答案
1.B 【解析】 根据题意得,y=-x2+70x-800=-(x-35)2+425,当x=35时,y有最大值.故选B.
知识点 利用二次函数解决利润最大问题
2.某商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1 558,其中15≤x≤22,那么一周可获得的最大利润是 ( )
A.2
数学·九年级下册·北师
1 二次函数
1.[2020上海长宁区一模]下列函数中,y是x的二次函数的是 ( )
A.y=1????2B.y=x2-1
C.y=3x+1 D.y=(x-1)2-x2
?
答案
1.B 【解析】 A项,y=1????2右边不是整式,故y不是x的二次函数;C项,y=3x+1是一次函数;D项,y=(x-1)2-x2=-2x+1,不是二次函数.故选B.
?
知识点1 二次函数的概念
判定一个函数是否为二次函数的方法
(1)先将函数进行整理,使其右边是含自变量的代数式,左边是因变量;(2)判定右边含自变量的代数式是否为整式;(3)判定含自变量的项的最高次数是否为2;(4)判定二次项的系数是否为0.
归纳总结
2.二次函数y=(x-2)(2x+1)化为一般式为 ,其中a= ,b= ,c= .?
答案
2.y=2x2-3x-2 2 -3 -2
知识点1 二次函数的概念
3.易错题 若函数y=(m2+m)????????2?2?????1是关于x的二次函数,则m的值是 .?
?
答案
3.3 【解析】 由题意,得????2+????≠0,????2?2?????1=2,解得????≠0且????≠?1,????=?1或????=3,因此当m=3时,该函数是关于x的二次函数.
?
知识点1 二次函数的概念
4.[2020浙江金华七校联考]已知关于自变量x的函数y=(m2-m)x2+(m-1)x+m+1.
(1)若该函数是一次函数,则m应满足什么条件?
(2)若该函数是二次函数,则m应满足什么条件?
答案
4.【解析】 (1)若该函数是一次函数,则????2?????=0,?????1≠0,
解得????=0或????=1,????≠1,所以m=0,
因此若该函数是一次函数,则m=0.
(2)若该函数是二次函数,则m2-m≠0,
解得m≠0且m≠1,
因此若该函数是二次函数,则m≠0且m≠1.
?
知识点1 二次函数的概念
5.现有长为24 m的篱笆,一面利用围墙围成如图所示的中间隔有一道篱笆的矩形花圃,设花圃垂直于墙的一边长为
x m,面积是S m2,则S与x之间的关系式是 ( )?
A.S=-3x2+24x B.S=-2x2-24x
C.S=-3x2-24x D.S=-2x2+24x
答案
5.A 【解析】 由题可知,与墙平行的一边长为(24-3x)m,所以S=x(24-3x)=-3x2+24x.故选A.
知识点2 列二次函数表达式
6.[2020安徽芜湖一模]某工厂今年一月份生产防疫护目镜的产量是20万件,计划接下来两个月增加产量,如果月平均增长率为x,那么第一季度防疫护目镜的产量y(万件)与x之间的关系式为 .?
答案
6. y=20x2+60x+60 【解析】 由题意知,一月,二月,三月的产量分别为20万件,20(x+1)万件,20(x+1)2万件,所以第一季度防疫护目镜的产量y(万件)与x之间的关系式为y=20+20(x+1)+20(x+1)2=20x2+60x+60.
知识点2 列二次函数表达式
7.已知一个菱形两条对角线的长的和为24 cm,设其中一条对角线的长为x cm,则该菱形的面积S(cm2)与x(cm)之间的函数关系式为 ,自变量x的取值范围是 .?
答案
7.S=-12x2+12x 0
知识点2 列二次函数表达式
8.某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满;当每个房间每天的定价每增加10元时,就会有1个房间空闲.设每个房间每天的定价增加x元(x为10的整数倍).求:
(1)房间每天的入住量y(间)关于x(元)的函数表达式;
(2)该宾馆每天的房间收费z(元)关于x(元)的函数表达式.
答案
8.【解析】 (1)由题意,得y=-110x+60,
即房间每天的入住量y关于x的函数表达式为y=-110x+60(0≤x≤600,且x为10的整数倍).
(2)由题意,得z=(200+x)(-110x+60)=-110x2+40x+12 000,
即该宾馆每天的房间收费z关于x的函数表达式为z=-110x2+40x+12 000(0≤x≤600,且x为10的整数倍).
?
知识点2 列二次函数表达式
9.如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10 cm,边CA与边MN在同一条直线上,开始时点A与点M重合,△ABC沿MN方向以1 cm/s的速度匀速运动,当点A与点N重合时,停止运动.设运动的时间为t s,运动过程中△ABC与正方形MNPQ的重叠部分的面积为S cm2.
(1)试写出S关于t的函数表达式,并指出自变量t的取值范围;
(2)当t=2时,重叠部分的面积是多少?
答案
9.【解析】 (1)设运动过程中,AB与MQ交于点R.
∵△ABC是等腰直角三角形,四边形MNPQ是正方形,
∴△AMR是等腰直角三角形.
由题意知,AM=MR=t cm,
∴S=S△AMR=12t·t=12t2(0≤t≤10).
(2)当t=2时,重叠部分的面积是12×22=2(cm2).
?
知识点2 列二次函数表达式
2 二次函数的图象与
性质
课时1 二次函数y=x2,y=-x2的图象与性质
课时1
1.已知正方形的边长为x cm,则它的面积y(cm2)与边长x(cm)的函数图象为 ( )
答案
1.C 【解析】 根据正方形面积公式可知,函数表达式为y=x2,其中x>0.故选C.
知识点1 二次函数y=x2的图象与性质
2.已知二次函数y=x2的图象经过点(1,y1),(2,y2),则y1,y2的大小关系是 ( )
A.y1=y2 B.y1>y2
C.y1
答案
2.C 【解析】 对于二次函数y=x2,当x>0时,y的值随x值的增大而增大,因为1<2,所以y1
知识点1 二次函数y=x2的图象与性质
3.关于函数y=x2,下列说法正确的是 ( )
A.y的值随着x的增大而增大
B.y的值随着x的增大而减小
C.函数有最小值
D.无论x取何值,y的值总为正
答案
3.C 【解析】 对于函数y=x2,当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大,故A,B错误;当x=0时,y=0,函数有最小值,故D错误,C正确.故选C.
知识点1 二次函数y=x2的图象与性质
4.若点A(2,m)在二次函数y=x2的图象上,则m= ,点A关于x轴的对称点B的坐标是 ,点A关于y轴的对称点C的坐标是 ,B,C两点中在抛物线y=x2上的点是 .?
答案
4.4 (2,-4) (-2,4) C
知识点1 二次函数y=x2的图象与性质
5.下列各点中,在二次函数y=-x2图象上的是 ( )
A.(23,-6) B.(-23,6)
C.(-23,12) D.(23,-12)
?
答案
5.D 【解析】 当x=23时,y=-(23)2=-12,故点(23,-12)在二次函数y=-x2的图象上.故选D.
?
知识点2 二次函数y=-x2的图象与性质
判断点是否在函数图象上的方法
将点的横坐标代入函数表达式,若求出的函数值等于该点的纵坐标,则该点在函数图象上;若求出的函数值不等于该点的纵坐标,则该点不在函数图象上.
归纳总结
6.[2019海南海口龙华区期中]抛物线y=-x2不具有的性质是 ( )
A.开口向下 B.对称轴是y轴
C.与y轴不相交 D.最高点是原点
答案
6.C 【解析】 抛物线y=-x2与y轴相交于坐标原点(0,0).故选C.
知识点2 二次函数y=-x2的图象与性质
7.关于二次函数y=x2和y=-x2的图象,以下说法正确的有 .(填序号)?
①两图象都关于x轴对称;②两图象都关于y轴对称;③两图象的顶点相同;④两图象的开口方向不同;⑤点(-1,1)在抛物线y=x2上,也在抛物线y=-x2上.
答案
7.②③④ 【解析】 因为二次函数y=x2的图象开口向上,对称轴是y轴,顶点坐标是(0,0),二次函数y=-x2的图象开口向下,对称轴是y轴,顶点坐标是(0,0),所以②③④正确,①不正确;把点(-1,1)分别代入y=x2和y=-x2验证,可知点(-1,1)在抛物线y=x2上,不在抛物线y=-x2上,所以⑤不正确.
知识点2 二次函数y=-x2的图象与性质
(1)对于二次函数的研究,一般从图象的开口方向、顶点坐标、对称轴,以及函数增减性、最大(小)值等方面展开;(2)二次函数y=x2和y=-x2的图象关于x轴对称.
名师点睛
8.二次函数y=-x2图象的顶点坐标是 ,若点(a,-4)在其图象上,则a的值是 .?
答案
8.(0,0) ±2 【解析】 二次函数y=-x2图象的顶点坐标是(0,0),∵点(a,-4)在其图象上,∴-a2=-4,解得a=±2.
知识点2 二次函数y=-x2的图象与性质
9.函数y=x2与y=-x2的图象关于 对称,也可以认为函数y=-x2的图象是由函数y=x2的图象绕 旋转后得到的.?
答案
9.x轴 原点
知识点2 二次函数y=-x2的图象与性质
10.已知点A(-2,m),B(3,n)都是抛物线y=-x2上的点,则m与n的大小关系是 .?
答案
10.m>n 【解析】 由题意知,m=-(-2)2=-4,n=-32=-9,所以m>n.
知识点2 二次函数y=-x2的图象与性质
11.已知函数y=????2????????2?2是关于x的二次函数.
(1)求满足条件的k的值;
(2)当k为何值时,抛物线有最高点?求出这个最高点,并求x为何值时,y随x的增大而增大?
(3)当k为何值时,函数有最小值?最小值是多少?并求x为何值时,y随x的增大而减小?
?
知识点2 二次函数y=-x2的图象与性质
答案
11.【解析】 (1)∵函数y=????2????????2?2是关于x的二次函数,
∴k2-2=2,且????2≠0,
∴k=±2.
(2)当抛物线有最高点时,
图象开口向下,即????2<0,
∴k=-2,
∴最高点为(0,0),当x<0时,y随x的增大而增大.
(3)当函数有最小值时,
图象开口向上,即????2>0,
∴k=2,
∴最小值为0,当x<0时,y随x的增大而减小.
?
知识点2 二次函数y=-x2的图象与性质
12.已知点M(-2,m)在抛物线y=-x2上,过点M作MN∥x轴,交抛物线于另一点N,求△MON的面积.
答案
12.【解析】 将点M(-2,m)代入抛物线y=-x2,得m=-4,
∴点M(-2,-4).
∵MN∥x轴,点M,N在抛物线上,
∴点M,N关于y轴对称,∴N(2,-4),MN=4,
∴S△MON=12×4×4=8.
?
知识点2 二次函数y=-x2的图象与性质
1.在同一平面直角坐标系中,二次函数y=x2与一次函数y=-x-1的图象大致为 ( )
答案
1.D
2.[2019湖北咸宁中考]已知点A(-1,m),B(1,m),C(2,m-n)(n>0)在同一个函数的图象上,这个函数可能是 ( )
A.y=xB.y=-2????
C.y=x2D.y=-x2
?
答案
2.D 【解析】 ∵A(-1,m),B(1,m),∴点A与点B关于y轴对称.∵n>0,∴m-n
A.h<1 B.h=1 C.1
3.B 【解析】 如图,过点C作CE⊥AB于点E,设斜边AB交y轴于点D,连接CD.由题意设A(-a,a2)(a>0),B(a,a2),C(b,b2)
(b>0),D(0,a2),则斜边上的高为h=a2-b2.∵△ABC是直角三角形,∴CD=a,在Rt△CDE中,CE2+DE2=CD2,即h2+b2=a2,
∴h2=h,∴h=1.故选B.
4.[2019湖南衡阳中考]在平面直角坐标系中,抛物线y=x2如图所示.已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4??依次进行下去,则点A2 019的坐标为 .?
答案
4.(-1 010,1 0102) 【解析】 易知点A,A1关于y轴对称,点A2,A3关于y轴对称??点A1的坐标为(-1,1),∴直线A1A2的表达式为y=x+2,令x+2=x2,解得x1=-1(舍去),x2=2,故点A2的坐标为(2,4),∴点A3的坐标为(-2,4).同理可得A5(-3,9)??以此类推,可知点An(n为奇数)的坐标为(-????+12,(????+12)2),故点A2 019的坐标为(-1 010,1 0102).
?
5.定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1
?
答案
5.①③
6.如图,圆的半径为2,C1是二次函数y=x2的图象,C2是二次函数y=-x2 的图象,则阴影部分的面积是 .?
答案
6.2π 【解析】 由二次函数y=x2和y=-x2的图象关于x轴对称,可知阴影部分的面积即圆面积的一半,所以阴影部分的面积是12π×22=2π.
?
7.已知a>1,点(a-1,y1),(a,y2),(a+1,y3)都在二次函数y=x2的图象上,则y1,y2,y3之间的大小关系为 .?
答案
7.y3>y2>y1 【解析】 因为a>1,所以0
8.如图,正方形OABC的顶点B在抛物线y=x2上,且点B在第一象限,若点B的横坐标与纵坐标之和等于6,则正方形OABC的面积为 .?
答案
8.10 【解析】 因为正方形OABC的顶点B在抛物线y=x2上,且点B在第一象限,所以可设点B的坐标为(x,x2),x>0.因为点B的横坐标与纵坐标之和等于6,所以x+x2=6,解得x1=2,x2=-3(不合题意,舍去),所以B(2,4),所以OB2=22+42=20.因为OB2=OA2+AB2,OA=AB,所以正方形OABC的边长为10,所以正方形OABC的面积为OA2=10.
?
9.已知抛物线y=-x2与直线y=3x+m都经过点(2,n).
(1)画出函数y=-x2的图象,并求出m,n的值;
(2)两者是否存在另一个交点?若存在,请求出这个点的坐标;若不存在,请说明理由.
答案
9.【解析】 (1)函数y=-x2的图象如图所示.
∵抛物线y=-x2与直线y=3x+m都经过点(2,n),
∴n=-22,n=3×2+m,∴n=-4,m=-10.
(2)存在.
由题意得,????=3?????10,????=?????2,
解得????=?5,????=?25,或????=2,????=?4,
∴另一个交点的坐标为(-5,-25).
?
课时2 二次函数y=ax2,y=ax2+c的图象与性质
课时2
1.[2020上海闵行区模拟]若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点 ( )
A.(2,4) B.(-2,-4)
C.(-4,2) D.(4,-2)
答案
1.A 【解析】 因为二次函数y=ax2的图象的对称轴为y轴,所以若图象经过点P(-2,4),则该图象必经过点(2,4).故选A.
知识点1 二次函数y=ax2的图象与性质
2.易错题 若抛物线y=m????????2+????的开口向下,则m的值为 ( )
A.-1 B.-2
C.1 D.1或-2
?
答案
2.B 【解析】 根据题意,得m2+m=2且m<0,∴m=-2.故选B.
知识点1 二次函数y=ax2的图象与性质
3.关于抛物线y=12x2,y=x2,y=-x2,给出下列结论:①都是开口向上;②都以点(0,0)为顶点;③都以y轴为对称轴;④都关于x轴对称.其中正确的个数有( )
A.1 B.2 C.3 D.4
?
答案
3.B 【解析】 抛物线y=12x2,y=x2开口向上,y=-x2开口向下,所以①错误;抛物线y=12x2,y=x2,y=-x2都以点(0,0)为顶点,都以y轴为对称轴,所以②③正确,④错误.故选B.
?
知识点1 二次函数y=ax2的图象与性质
4.[2020山东德州模拟]给出下列函数:①y=3x+2;②y=3????;③y=2x2;④y=-3x2.其中符合条件“当x>1时,函数值y随自变量x增大而增大”的是 ( )
A.①③ B.③④ C.②④ D.②③
?
答案
4.A 【解析】 ①y=3x+2,当x>1时,函数值y随自变量x增大而增大,故①符合题意.②y=3????,当x>1时,函数值y随自变量x增大而减小,故②不符合题意.③y=2x2,当x>1时,函数值y随自变量x增大而增大,故③符合题意.④y=-3x2,当x>1时,函数值y随自变量x增大而减小,故④不符合题意.故选A.
?
知识点1 二次函数y=ax2的图象与性质
5.[2020内蒙古呼和浩特期中]已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是 .(请用“>”连接)?
答案
5. a1>a2>a3>a4 【解析】 由题图,可知抛物线y=a1x2与y=a2x2的开口向上,其中前者开口小,所以a1>a2>0,抛物线y=a3x2与y=a4x2的开口向下,其中后者开口小,所以a4
知识点1 二次函数y=ax2的图象与性质
6.若点A(x1,4),B(x2,4)(x1≠x2)均在抛物线y=ax2上,则当x=x1+x2时,y的值是 .?
答案
6.0 【解析】 由题可知,点A,B关于y轴对称,所以x=x1+x2=0,故y的值为0.
知识点1 二次函数y=ax2的图象与性质
7.函数y=x2+1的图象大致是 ( )
答案
7.C 【解析】 函数y=x2+1的图象开口向上,顶点是(0,1).故选C.
知识点2 二次函数y=ax2+c的图象与性质
8.[2020浙江杭州期末]关于二次函数y=-2x2-2,下列说法正确的是 ( )
A.图象开口向上
B.当x<0时,y随x的增大而增大
C.图象的对称轴是x=1
D.当x=0时,y有最大值-12
?
答案
8.B 【解析】 因为二次函数y=-2x2-2,a=-2<0,所以该函数图象开口向下,当x<0时,y随x的增大而增大,故A错误,B正确;二次函数y=-2x2-2图象的对称轴是x=0,顶点坐标为(0,-2),所以当x=0时,y有最大值-2,故C,D错误.故选B.
知识点2 二次函数y=ax2+c的图象与性质
9.已知直线y=2x与抛物线y=ax2+3的一个交点为(2,b).
(1)求a,b的值;
(2)若直线y=2x上纵坐标为2的点为A,抛物线y=ax2+3的顶点为B,求△AOB的面积S.
答案
9.【解析】 (1)∵点(2,b)在直线y=2x上,∴b=4.
∵点(2,b)即点(2,4)在抛物线y=ax2+3上,
∴4a+3=4,∴a=14.
(2)在y=2x中,令y=2,得x=1,∴A(1,2),
又∵抛物线y=14x2+3的顶点为B(0,3),
∴△AOB的面积S=12×3×1=32.
?
知识点2 二次函数y=ax2+c的图象与性质
10.[2020江苏盐城期末]把抛物线y=12x2向下平移2个单位长度,得到的抛物线的表达式为 ( )
A.y=12x2+2 B.y=12x2-2
C.y=12(x+2)2?D.y=12(x-2)2
?
答案
10.B 【解析】 二次函数y=12x2的顶点坐标为(0,0),向下平移2个单位长度得对应点的坐标为(0,-2),所以平移后抛物线的表达式为y=12x2-2.故选B.
?
知识点3 二次函数y=ax2+c与y=ax2的图象之间的关系
11.已知二次函数y=ax2+c与y=-5x2的图象形状相同、方向相反,且其顶点坐标是(0,3),则其表达式为 .?
答案
11.y=5x2+3 【解析】 ∵二次函数y=ax2+c与y=-5x2的形状相同、方向相反,∴a=5.∵抛物线的顶点坐标是(0,3),∴c=3,∴其表达式为y=5x2+3.
知识点3 二次函数y=ax2+c与y=ax2的图象之间的关系
12.易错题 能否通过适当地上下平移二次函数y=13x2的图象,使得到的新的函数图象过点(3,-3)?若能,说出平移的方向和距离;若不能,说明理由.
?
答案
12.【解析】 能.
把函数y=13x2的图象向下平移6个单位长度,得到的图象对应的函数表达式为y=13x2-6,该函数的图象过点(3,-3).
?
知识点3 二次函数y=ax2+c与y=ax2的图象之间的关系
1.在同一平面直角坐标系中,y关于x的一次函数y=-mx+n2与二次函数y=x2+m的图象可能是 ( )
答案
1.D
解答双图象问题的方法
(1)分类讨论法:根据函数表达式中系数的正负分类讨论.(2)逐项排除法:假定选项中的某一个函数图象正确,然后判断另一个函数图象是否合理;或根据两函数图象确定系数的取值范围,取值范围相同的正确,取值范围不同的错误.
归纳总结
2.易错题 已知拋物线y=-13x2+2,当1≤x≤5时,y的最大值是 ( )
A.2 B.23 C.53 D.73
?
答案
2.C 【解析】 ∵拋物线y=-13x2+2的二次项系数a=-13<0,∴该抛物线的开口向下,又∵其对称轴就是y轴,∴当1≤x≤5时,拋物线y=-13x2+2是下降的,∴当x=1时,y取得最大值,y最大=-13+2=53.故选C.
?
3.点A(-1,y1),B(2,y2),C(3,y3)都在二次函数y=(a2+1)x2+2的图象上,则y1,y2,y3的大小关系是 ( )
A.y1
C.y1>y3>y2 D.y2
3.A 【解析】 因为a2+1>0,所以y=(a2+1)x2+2的图象开口向上,又因为对称轴为y轴,所以当x>0时,y随x的增大而增大.因为A(-1,y1)关于y轴的对称点的坐标为(1,y1),且1<2<3,所以y1
A.10 B.8 C.6 D.4
?
答案
4.B 【解析】 如图,∵两抛物线表达式的二次项系数相同,∴两抛物线的形状完全相同.过抛物线y2=-12x2-1的顶点(0,-1)作平行于x轴的直线与抛物线y1=-12x2+1围成封闭图形,过点(0,-3)作平行于x轴的直线与抛物线y2=-12x2-1围成封闭图形,则这两个封闭图形的面积相等,故所求阴影部分的面积为4×2=8.故选B.
?
5.[2020安徽蚌埠期中]已知抛物线y=14x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等.如图,点M的坐标为(3,3),P是抛物线y=14x2+1上的一个动点,则△PMF周长的最小值是 ( )?
A.3 B.4 C.5 D.6
?
答案
5.C 【解析】 过点P作PE⊥x轴于点E,由题意可知,FP=PE,∴当点M,P,E三点共线时(如图所示),△PMF周长最小.易知ME∥y轴,∵F(0,2),M(3,3),∴ME=3,FM=(3?0)2+(3?2)2=2,∴△PMF周长的最小值为MP+FP+FM=ME+
FM=3+2=5.故选C.
?
6.已知抛物线y=mx2+m-2的顶点在y轴的负半轴上,且开口向上,则m的取值范围是 .?
答案
6.0
①只有当x=0时,y才有最大(或最小)值;②对于一切x的值,y都是负数;③当a>0时,y随x的增大而减小;④当a<0时,y随x的增大而减小.
答案
7.②③④ 【解析】 当x=0时,y有最大(或最小)值,且最大(或最小)值是-3,①正确;当a<0时,y的值可能为正数,②不正确;当a>0,x<0时,y随x的增大而增大,③不正确;当a<0,x>0时,y随x的增大而增大,④不正确.综上,不正确的是②③④.
8.已知抛物线y=x2-k的顶点为P,与x轴交于点A,B,且△ABP是等边三角形,则k的值是 .?
答案
8.3 【解析】 如图,由题意可知,k>0,点P的坐标为(0,-k),PO=k,OA=OB,AB=AP=BP,∠OPB=30°,∴tan 30°=????????????????,即????????????=33,解得OB=33k,∴点B的坐标为(33k,0).∵点B在抛物线y=x2-k上,∴将(33k,0)代入y=x2-k,得(33k)2-k=0,解得k1=0(不合题意,舍去),k2=3.故k的值为3.
?
9.已知二次函数y=mx2+1与反比例函数y=????????的图象有一个公共点(-1,-1).
(1)求二次函数和反比例函数的表达式;
(2)能否找到自变量x的取值范围,使二次函数、反比例函数的函数值都随x值的增大而减小?若能,写出这个取值范围;若不能,说明理由.
?
答案
9.【解析】 (1)因为两个函数的图象有一个公共点(-1,-1),
所以-1=m×(-1)2+1,-1=?????1,
所以m=-2,k=1,
所以二次函数的表达式为y=-2x2+1,反比例函数的表达式为y=1????.?
(2)能.
如图所示是二次函数y=-2x2+1和反比例函数y=1????在同一平面直角坐标系中的图象,
根据图象可知存在这样的自变量x的取值范围,
即当x>0时,二次函数、反比例函数的函数值都随x值的增大而减小.
?
10.如图,抛物线y=-12x2+2与x轴交于A,B两点,其中点A在x轴的正半轴上,点B在x轴的负半轴上.
(1)试写出该抛物线的对称轴和顶点C的坐标;
(2)在抛物线上是否存在一点M,使△MAC≌△OAC?若存在,求出点M的坐标;若不存在,请说明理由.
?
答案
10.【解析】 (1)抛物线的对称轴是y轴,顶点C的坐标为(0,2).
(2)不存在.理由如下:
由已知条件易得点A的坐标为(2,0),点B的坐标为(-2,0),
则OA=OB=OC=2,故三角形OAC是等腰直角三角形.
假设存在一点M,使△MAC≌△OAC,
因为AC为公共边,OA=OC,
所以点M和O关于直线AC对称,
因此四边形OAMC是正方形,所以点M的坐标为(2,2).
当x=2时,y=-12x2+2=-12×22+2=0≠2,
即点M不在抛物线y=-12x2+2上,
所以在抛物线上不存在一点M,使得△MAC≌△OAC.
?
课时3 二次函数y=a(x-h)2,y=a(x-h)2+k的图象与性质
课时3
1.二次函数y=3(x-2)2的图象的对称轴是( )
A.直线x=2 B.直线x=-2
C.y轴 D.x轴
答案
1.A
知识点1 二次函数y=a(x-h)2的图象与性质
2.二次函数y=3(x+1)2的图象不经过的象限是 ( )
A.第一、二象限 B.第二、四象限
C.第三、四象限 D.第二、三象限
答案
2.C 【解析】 因为二次函数y=3(x+1)2的图象开口向上,顶点为(-1,0),对称轴是直线x=-1,与y轴的交点是(0,3),所以二次函数y=3(x+1)2的图象经过第一、二象限,不经过第三、四象限.故选C.
知识点1 二次函数y=a(x-h)2的图象与性质
3.[2020河南焦作一模]若抛物线y=2(x-1)2经过(m,n)和(m+3,n)两点,则n的值为 ( )
A.92 B.-92 C.1 D.-12
?
答案
3.A 【解析】 由抛物线y=2(x-1)2经过(m,n)和(m+3,n)两点,可知该抛物线的对称轴为直线x=????+????+32=1,所以m=-12,将点(-12,n)代入函数表达式,得n=2(-12-1)2=92.故选A.
?
知识点1 二次函数y=a(x-h)2的图象与性质
4.[2020湖北鄂州期中]对于抛物线y=35(x-1)2,给出下列说法:①顶点坐标为(1,0);②对称轴为直线x=0;③有最低点;④当x>1时,y的值随x值的增大而增大;⑤当x=1时,y取最大值0.
其中正确的是 .(填序号)?
?
答案
4.①③④ 【解析】 因为抛物线y=35(x-1)2,所以顶点坐标为(1,0),对称轴为直线x=1,开口向上,有最低点,当x=1时,y取最小值0,当x>1时,y的值随x值的增大而增大,当x<1时,y的值随x值的增大而减小.故说法正确的是①③④.
?
知识点1 二次函数y=a(x-h)2的图象与性质
5.已知二次函数y=a(x-h)2,当x=2时,有最大值,且图象过点(1,-3),求该函数的表达式,并指出当x为何值时,y随x的增大而减小.
答案
5.【解析】 ∵当x=2时,二次函数y=a(x-h)2有最大值,
∴h=2,a<0,
又∵函数图象过点(1,-3),∴-3=a(1-2)2,解得a=-3,
∴该函数的表达式为y=-3(x-2)2.
当x>2时,y随x的增大而减小.
知识点1 二次函数y=a(x-h)2的图象与性质
6.[2020北京海淀区一模]将抛物线y=2x2向左平移3个单位长度后,所得到的抛物线的函数表达式为 ( )
A.y=2x2-3 B.y=2x2+3
C.y=2(x-3)2 D.y=2(x+3)2
答案
6.D 【解析】 抛物线y=2x2的顶点坐标为(0,0),向左平移3个单位长度后,顶点坐标变为(-3,0),所以平移后的抛物线的函数表达式为y=2(x+3)2.故选D.
知识点2 二次函数y=a(x-h)2,y=a(x-h)2+k与y=ax2的图象之间的关系
7.[2020黑龙江哈尔滨中考]将抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,所得到的抛物线的表达式为 ( )
A.y=(x+3)2+5 B.y=(x-3)2+5
C.y=(x+5)2+3 D.y=(x-5)2+3
答案
7.D 【解析】 解法一 根据抛物线的平移规律“左加右减(自变量),上加下减(常数项)”可知,抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,得到抛物线y=(x-5)2+3.
解法二 易知抛物线y=x2的顶点坐标是(0,0),将点(0,0)向上平移3个单位长度,再向右平移5个单位长度,得到点(5,3),即平移后抛物线的顶点坐标是(5,3),所以平移后得到抛物线y=(x-5)2+3.
知识点2 二次函数y=a(x-h)2,y=a(x-h)2+k与y=ax2的图象之间的关系
8.二次函数y=(x+2)2-1的图象大致为 ( )
答案
8.D 【解析】 抛物线y=(x+2)2-1的顶点坐标为(-2,-1),且开口向上.故选D.
知识点3 二次函数y=a(x-h)2+k的图象与性质
9.[2019甘肃兰州中考]已知点A(1,y1),B(2,y2)在抛物线y=-(x+1)2+2上,则下列结论正确的是 ( )
A.2>y1>y2 B.2>y2>y1
C.y1>y2>2 D.y2>y1>2
答案
9.A 【解析】 解法一 函数y=-(x+1)2+2有最大值2,图象开口向下,当x>-1时,y随x的增大而减小.∵-1<1<2,
∴2>y1>y2. 故选A.
解法二 函数y=-(x+1)2+2有最大值2,当x=1时,y1=-(1+1)2+2=-2;当x=2时,y2=-(2+1)2+2=-7,∴2>y1>y2.故选A.
知识点3 二次函数y=a(x-h)2+k的图象与性质
10.[2020安徽亳州二调]如果抛物线y=(x-m)2+m+1的对称轴是直线x=1,那么它的顶点坐标为 .?
答案
10.(1,2) 【解析】 ∵抛物线y=(x-m)2+m+1的对称轴是直线x=1,∴m=1,∴抛物线的表达式为y=(x-1)2+2,∴顶点坐标为(1,2).
知识点3 二次函数y=a(x-h)2+k的图象与性质
11.对于抛物线y=-12(x+3)2-1,给出下列说法:①抛物线的开口向下;②对称轴为直线x=3;③顶点坐标为(-3,1);④当x>3时,y随x的增大而减小.其中正确的有 .(填序号)?
?
答案
11.①④ 【解析】 因为a<0,所以抛物线开口向下,①正确;抛物线对称轴为直线x=-3,②错误;顶点坐标为(-3,-1),
③错误;当x>-3时,y随x的增大而减小,对于x>3时当然也成立,④正确.故正确的有①④.
知识点3 二次函数y=a(x-h)2+k的图象与性质
12.如图是二次函数y=(x+m)2+k的图象,其顶点为点M(1,-4).
(1)求二次函数的图象与x轴的交点A,B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=54S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
?
知识点3 二次函数y=a(x-h)2+k的图象与性质
答案
12.【解析】 (1)∵(1,-4)是二次函数y=(x+m)2+k图象的顶点坐标,
∴y=(x-1)2-4=x2-2x-3.
令y=0,则x2-2x-3=0,解得x1=-1,x2=3,
∴A,B两点的坐标分别为(-1,0),(3,0).
(2)在二次函数的图象上存在点P,使S△PAB=54S△MAB.
设点P(x,y),由(1)知AB=4,
则S△PAB=12AB×|y|=2|y|,
∵S△MAB=12AB×|-4|=8,
∴2|y|=54×8,解得y=±5.
?
知识点3 二次函数y=a(x-h)2+k的图象与性质
答案
∵二次函数的最小值为-4,∴y=5.
当y=5时,x=-2或x=4.
故存在点P,使S△PAB=54S△MAB,点P的坐标为(-2,5)或(4,5).
?
知识点3 二次函数y=a(x-h)2+k的图象与性质
1.[2019河北唐山路南区期中]抛物线y=(x+2)2+m2+1(m为常数)的顶点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
1.B 【解析】 ∵y=(x+2)2+m2+1,∴顶点坐标为(-2,m2+1),∵-2<0,m2+1>0,∴顶点在第二象限.故选B.
2.[2020黑龙江哈尔滨平房区一模]已知抛物线y=(x+2)2-1向左平移h个单位长度,向下平移k个单位长度,得到的抛物线的表达式为y=(x+3)2-4,则h和k的值分别为 ( )
A.1,3 B.3,-4 C.1,-3 D.3,-3
答案
2.A 【解析】 解法一 因为抛物线y=(x+2)2-1的顶点坐标是(-2,-1),所以向左平移h个单位长度,向下平移k个单位长度后的坐标为(-2-h,-1-k),所以平移后抛物线的表达式为y=(x+2+h)2-1-k.因为平移后抛物线的表达式为y=(x+3)2-4,所以2+h=3,-k-1=-4,所以h=1,k=3.故选A.
解法二 根据抛物线的平移规律“左加右减,上加下减”得到平移后的抛物线为y=(x+2+h)2-1-k=(x+3)2-4,所以2+h=3,-1-k=-4,所以h=1,k=3.故选A.
3.已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象是 ( )
答案
3.A 【解析】 因为二次函数的图象开口向上,所以a>0.因为二次函数的图象的顶点坐标为(1,-c),且由图象知,顶点在第四象限,所以c>0,故一次函数y=ax+c的图象经过第一、二、三象限.故选A.
4.已知二次函数y=3(x+1)2-4的图象上有三点A(-2,y1),B(1,y2),C(2,y3),则y1,y2,y3的大小关系为 ( )
A.y1>y2>y3 B.y2>y1>y3
C.y3>y2>y1 D.y3>y1>y2
答案
4.C 【解析】 由抛物线的对称性可知,点A(-2,y1)在抛物线上的对称点为A'(0,y1),对于抛物线y=3(x+1)2-4,当x>-1时,y随x的增大而增大,所以y3>y2>y1.故选C.
5.[2020浙江温州模拟]已知抛物线y=a(x-2)2+1经过点A(m,y1),B(m+2,y2),若点A在抛物线对称轴的左侧,且1
5.C 【解析】 因为抛物线y=a(x-2)2+1的顶点坐标为(2,1),且1
6.易错题已知二次函数y=-(x-h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为-1,则h的值为 ( )
A.3或6 B.1或6 C.1或3 D.4或6
答案
6.B 【解析】 如图,分h<2,2≤h≤5和h>5三种情况讨论.当h<2时,有-(2-h)2=-1,解得h1=1,h2=3(舍去).当2≤h≤5时,y=-(x-h)2的最大值为0,不符合题意.当h>5时,有-(5-h)2=-1,解得h3=4(舍去),h4=6.综上所述,h的值为1或6.故选B.
7.把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的函数表达式为 .?
答案
7.y=-(x+1)2-2 【解析】 二次函数y=(x-1)2+2图象的顶点坐标为(1,2),绕原点旋转180°后顶点坐标变为(-1,-2),所以旋转后得到的图象的函数表达式为y=a(x+1)2-2,因为旋转过程中开口大小不变,仅开口方向改变,所以a=-1,即旋转后得到的图象的函数表达式为y=-(x+1)2-2.
8.已知二次函数y=-(x-m)2+1,当x>3时,y随x的增大而减小,则m的取值范围是 .?
答案
8.m≤3 【解析】 对于二次函数y=-(x-m)2+1,当x>m时,y随x的增大而减小,结合题意可知m≤3.
9.如图,把抛物线y=x2沿直线y=x平移2个单位长度后,其顶点在直线y=x上的点A处,则平移后抛物线所对应的函数表达式是 .?
?
答案
9.y=(x-1)2+1 【解析】 把抛物线y=x2沿直线y=x平移2个单位长度,即将抛物线y=x2向上平移1个单位长度后再向右平移1个单位长度,所以平移后的抛物线所对应的表达式为y=(x-1)2+1.
?
10.[2020吉林长春一模]如图,在平面直角坐标系中,抛物线y=a(x+1)2+b与y=a(x-2)2+b+1交于点A.过点A作y轴的垂线,分别交两抛物线于点B,C(点B在点A左侧,点C在点A右侧),则线段BC的长为 .?
答案
10.6 【解析】 设抛物线y=a(x+1)2+b的对称轴与线段BC交于点E,抛物线y=a(x-2)2+b+1的对称轴与线段BC交于点F,如图所示.由抛物线的对称性,可知BE=AE,CF=AF,所以BC=BE+AE+AF+CF=2(AE+AF)=2×[2-(-1)]=6.
11.已知抛物线y=a(x+m)2的顶点坐标为(-1,0),且经过点A(-2,-12).
(1)求该抛物线对应的函数表达式;
(2)该抛物线是否经过点B(2,-2)?若不经过,怎样沿x轴方向平移,才能使它经过点B?并写出平移后的抛物线对应的函数表达式.
?
答案
11.【解析】 (1)∵抛物线y=a(x+m)2的顶点坐标为(-1,0),
∴m=1,
∵抛物线y=a(x+1)2经过点A(-2,-12),
∴a(-2+1)2=-12,解得a=-12,
∴该抛物线对应的函数表达式为y=-12(x+1)2.
?
答案
(2)不经过.
当x=2时,y=-12×(2+1)2=-92≠-2,
∴抛物线y=-12(x+1)2不经过点B(2,-2).
设平移后的抛物线对应的函数表达式为y=-12(x+1+n)2,
∵它经过点B(2,-2),∴-12(2+1+n)2=-2,
解得n=-1或n=-5,
∴将抛物线y=-12(x+1)2向右平移1个或5个单位长度,即可使它经过点B(2,-2),平移后的抛物线对应的函数表达式为y=
-12x2或y=-12(x-4)2.
?
12.如图,顶点为M的抛物线y=a(x+1)2-4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,-3).
(1)求抛物线的表达式;
(2)判断△BCM是否为直角三角形,并说明理由;
(3)在该抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
答案
12.【解析】 (1)∵抛物线y=a(x+1)2-4与y轴相交于点C(0,-3),∴-3=a(0+1)2-4,∴a=1.
∴抛物线的表达式为y=(x+1)2-4,即y=x2+2x-3.
(2)△BCM为直角三角形.理由如下:
解法一 将y=0代入y=x2+2x-3中,得
x2+2x-3=0,解得x1=-3,x2=1,
∴A(1,0),B(-3,0).∵C(0,-3),
∴OC=OB,∴∠OCB=45°.
如图1,过点M作MH⊥y轴于点H,由(1)知M(-1,-4),
则MH=CH=1,∴∠MCH=45°,
∴∠BCM=180°-∠OCB-∠MCH=90°,
∴△BCM为直角三角形.?
答案
解法二 将y=0代入y=x2+2x-3中,得x2+2x-3=0,
解得x1=-3,x2=1,
∴A(1,0),B(-3,0).
易得顶点M的坐标为(-1,-4).
在Rt△BOC中,由勾股定理得BC2=32+32=18,
∵C(0,-3),∴CM2=[(-3)-(-4)]2+12=2,
BM2=[(-1)-(-3)]2+42=20,
∴BC2+CM2=BM2,∴△BCM为直角三角形.
(3)存在.∵B(-3,0),C(0,-3),∴直线BC的表达式为y=-x-3.
在等腰直角三角形OBC中,OB=OC=3,
∴BC=32,同理可得CM=2.
由(2)可知,△BCM是直角三角形,∠BCM=90°,∴S△BCM=12×BC×CM=3.
?
答案
设点N的坐标为(t,t2+2t-3).
①当点N位于x轴的下方时,点N只能位于直线BC的下方.
如图2,过点N作ND∥y轴交BC于点D,连接BN,CN,
则D(t,-t-3),
∴DN=(-t-3)-(t2+2t-3)=-t2-3t.
∴S△BCN=S△BDN+S△CDN=-32t2-92t.
由已知得S△BCN=S△BCM,∴-32t2-92t=3,
解得t1=-2,t2=-1(舍去).
∴点N的坐标为(-2,-3).
②当点N位于x轴的上方时,
过点N作NE⊥x轴于点E,连接AN,BN,
则S△ABN=12×AB×NE=2t2+4t-6.
?
答案
由已知得S△ABN=S△BCM,∴2t2+4t-6=3,解得t=?2±222.
∴点N的坐标为(?2+222,32)或(?2?222,32).
综上所述,共存在3个满足条件的点N,它们的坐标分别为(-2,-3),(?2+222,32),(?2?222,32).
?
判断△BCM为直角三角形可通过证明三角形的一个内角是直角获得,也可通过勾股定理的逆定理获得.对于最后一问这种类型的题,当点的位置不确定时要分类讨论.
名师点睛
课时4 二次函数y=ax2+bx+c的图象与性质
课时4
1.将二次函数y=x2-4x+5化成y=a(x-h)2+k的形式为 ( )
A.y=(x-2)2+1 B.y=(x+2)2+1
C.y=(x-2)2+9 D.y=(x-4)2+1
答案
1.A 【解析】 y=x2-4x+5=x2-4x+4+1=(x-2)2+1.
知识点1 二次函数y=ax2+bx+c与y=a(x-h)2+k的关系
2.[2019山东济宁中考]将抛物线y=x2-6x+5向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线表达式是 ( )
A.y=(x-4)2-6 B.y=(x-1)2-3
C.y=(x-2)2-2 D.y=(x-4)2-2
答案
2.D 【解析】 y=x2-6x+5=(x-3)2-4,所以向上平移两个单位长度,再向右平移一个单位长度,平移后得到的抛物线表达式为y=(x-4)2-2.故选D.
知识点1 二次函数y=ax2+bx+c与y=a(x-h)2+k的关系
3.[2019重庆中考A卷]抛物线y=-3x2+6x+2的对称轴是 ( )
A.直线x=2 B.直线x=-2
C.直线x=1 D.直线x=-1
答案
3.C 【解析】 解法一 ∵y=-3x2+6x+2=-3(x-1)2+5,∴抛物线的对称轴为直线x=1.故选C.
解法二 ∵a=-3,b=6,c=2,∴抛物线y=-3x2+6x+2的图象的对称轴为直线x=-????2????=1.故选C.
?
知识点2 二次函数y=ax2+bx+c的图象与性质
4.[2020河北唐山期末]下列对二次函数y=2x2+x的描述,正确的是 ( )
A.图象开口向下
B.图象顶点坐标为(14,18)
C.图象经过原点
D.当x<0时,y随x值的增大而增大
?
答案
4.C 【解析】 ∵a=2,b=1,c=0,∴二次函数y=2x2+x的图象开口向上,顶点坐标为(-14,-18),故A,B项错误;二次函数y=2x2+x的图象的对称轴为直线x=-????2????=-14,当x<-14时,y随x值的增大而减小,当x>-14时,y随x值的增大而增大,故D项错误;当x=0时,y=2x2+x=0,∴二次函数y=2x2+x的图象经过原点,C项正确.故选C.
?
知识点2 二次函数y=ax2+bx+c的图象与性质
5.[2020湖北宜昌期中]二次函数y=ax2+bx+c的图象如图所示,若点A(-2.2,y1),B(-3.2,y2)是图象上的两点,则y1与y2的大小关系是 ( )?
A.y1
答案
5.A 【解析】 由题图,知该函数图象开口向下,对称轴是直线x=-3.因为点A(-2.2,y1),B(-3.2,y2)是图象上的两点,且点A到对称轴的距离大于点B到对称轴的距离,所以y1
6.易错题若抛物线y=ax2-x+c与y=2(x-3)2+1的对称轴相同,且两抛物线的顶点相距3个单位长度,则c的值为 .?
答案
6.112或-12 【解析】 抛物线y=2(x-3)2+1的对称轴是直线x=3,顶点坐标为(3,1).∵抛物线y=ax2-x+c与y=2(x-3)2+1的对称轴相同,∴-?12????=3,解得a=16.∵两抛物线的顶点相距3个单位长度,∴抛物线y=16x2-x+c的顶点坐标为(3,4)或(3,-2).把(3,4)代入y=16x2-x+c,得c=112;把(3,-2)代入y=16x2-x+c,得c=-12.综上,c的值为112或-12.
?
知识点2 二次函数y=ax2+bx+c的图象与性质
7.[2019浙江宁波中考]如图,已知二次函数y=x2+ax+3的图象经过点P(-2,3).
(1)求a的值和图象的顶点坐标.
(2)点Q(m,n)在该二次函数图象上.
①当m=2时,求n的值;
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
知识点2 二次函数y=ax2+bx+c的图象与性质
答案
7.【解析】 (1)把点P(-2,3)代入y=x2+ax+3中,得a=2.
∴y=x2+2x+3=(x+1)2+2,
∴图象的顶点坐标为(-1,2).
(2)①把x=2代入y=x2+2x+3,得y=11.
∴当m=2时,n=11.
②n的取值范围为2≤n<11.
∵点Q到y轴的距离小于2,
∴|m|<2,∴-2
知识点2 二次函数y=ax2+bx+c的图象与性质
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①a>0;②2a+b=0;③a+b+c>0;④当-1
A.1 B.2 C.3 D.4
答案
8.C 【解析】 ∵图象的开口向下,∴a<0,故①错误;由题图知对称轴为直线x=?1+32=1,∴-????2????=1,∴2a+b=0,故②正确;∵当x=1时,对应的y值大于0,∴a+b+c>0,故③正确;∵当-1
?
知识点3 二次函数y=ax2+bx+c的图象与a,b,c之间的关系
9.[2020甘肃四校联考]二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列四个结论:①ac<0;②4a+c<2b;③3b+2c<0;④当x>0时,y随x的增大而减小.其中正确的有 .(填序号)?
答案
9.①③④ 【解析】 ∵抛物线开口方向向下,∴a<0,∵抛物线与y轴正半轴相交,∴c>0,∴ac<0,①正确;∵x=0时,y>0,且对称轴为直线x=-1,∴当x=-2时,y>0,即4a-2b+c>0,∴4a+c>2b,②不正确;∵-????2????=-1,∴b=2a,当x=1时,y=a+b+c<0,
∴32b+c<0,∴3b+2c<0,③正确;由题中图象可知,当x>-1时,y随x的增大而减小,对于x>0时同样成立,④正确.故正确的有①③④.
?
知识点3 二次函数y=ax2+bx+c的图象与a,b,c之间的关系
1.如图,函数y=ax2-2x+1和y=ax-a(a是常数,且a≠0)在同一平面直角坐标系的图象可能是 ( )
答案
1.B 【解析】 抛物线y=ax2-2x+1过点(0,1),对称轴为直线x=1????.当a>0时,-a<0,1????>0,抛物线y=ax2-2x+1开口向上,对称轴在y轴右侧,直线y=ax-a经过第一、三、四象限,选项B符合题意,选项A,C不合题意;当a<0时,-a>0,1????<0,直线y=ax-a经过第一、二、四象限,抛物线y=ax2-2x+1开口向下,且对称轴在y轴左侧,选项D不符合题意.故选B.
?
2.已知二次函数y=ax2+(a+2)x-1(a为常数,且a≠0),则下列结论正确的是 ( )
A.若a>0,则当x<-1时,y随x的增大而增大
B.若a>0,则当x<-1时,y随x的增大而减小
C.若a<0,则当x<-1时,y随x的增大而增大
D.若a<0,则当x<-1时,y随x的增大而减小
答案
2.C 【解析】 ∵y=ax2+(a+2)x-1的对称轴为直线x=-????+22????=-12?1????.当a>0时,-1????<0,∴-12?1????<0,但大小无法确定,∴x<-1时,y随x增大的变化趋势无法判断;当a<0时,抛物线开口向下,-1????>0,∴-12?1????>-1,故当x<-1时,y随x的增大而增大.∴若a<0,则当x<-1时,y随x的增大而增大.故选C.
?
3.[2019山东烟台中考]已知二次函数y=ax2+bx+c的y与x的部分对应值如表:
给出下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0
答案
3.B 【解析】 因为x=0时,y=0,x=4时,y=0,所以抛物线的对称轴为直线x=2,故②正确.因为x=2时,y=-4,x=3时,y=-3>-4,对称轴为直线x=2,所以抛物线的开口向上,故①正确.由表格易知,③错误.抛物线与x轴的两个交点间的距离是4-0=4,故④正确.当A位于抛物线对称轴的右侧,B位于左侧时,x1>x2,故⑤错误.故选B.
x
-1
0
2
3
4
y
5
0
-4
-3
0
4.[2020河北唐山期末]已知二次函数y=x2-x+a(a>0),当自变量x取m时,其相应的函数值小于0,则下列结论正确的是 ( )
A.x取m-1时的函数值小于0
B.x取m-1时的函数值大于0
C.x取m-1时的函数值等于0
D.x取m-1时的函数值与0的大小关系不确定
答案
4.B 【解析】 由题意,画出函数y=x2-x+a(a>0)的大致图象如图所示.易知抛物线y=x2-x+a的对称轴为直线x=12.设抛物线与x轴交于点A,B,则A,B两点间的距离小于1,
∵x取m时,其相应的函数值小于0,∴观察图象可知,x=m-1在点A的左侧,∴当x=m-1时,y>0.故选B.
?
5.[2019湖北鄂州中考]二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.给出下列结论:①abc<0;②3a+c>0;
③(a+c)2-b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为 ( )?
A.1 B.2 C.3 D.4
答案
5.C 【解析】 ∵抛物线开口向上,∴a>0,∵抛物线的对称轴在y轴右侧,∴-????2????>0,∴b<0,∵抛物线与y轴交于负半轴,∴c<0,∴abc>0,①错误;当x=-1时,y>0,∴a-b+c>0,∵-????2????=1,∴b=-2a,把b=-2a代入a-b+c>0,得3a+c>0,②正确;当x=1时,y<0,∴a+b+c<0,又∵a-b+c>0,∴(a+b+c)(a-b+c)<0,∴(a+c)2-b2<0,③正确;∵抛物线的对称轴为直线x=1,∴x=1时,函数取得最小值,最小值为a+b+c,∴a+b+c≤am2+mb+c,a+b≤m(am+b),④正确.综上,②③④正确,共有3个.故选C.
?
6.[2020江苏无锡一模]已知抛物线y=-x2-2x+3,当-2≤x≤2时,对应的函数值y的取值范围为 .?
答案
6.-5≤y≤4 【解析】 y=-x2-2x+3=-(x+1)2+4,当x=-1时,二次函数有最大值4,当x=2时,y=-9+4=-5,∴-5≤y≤4.
7.[2020广东广州越秀区二段]如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,-2),且顶点在第三象限,设P=a-b+c,则P的取值范围是 .?
答案
7.-4
∴b=2-a>0,∴a<2.∵a>0,∴0
8.[2020河北保定期中]如图,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上有一点D(m,n)(m>0,n>0),使S△ABD=S△ABC,求点D的坐标.
答案
8.【解析】 (1)将A(3,0)代入y=-x2+2x+m,
得-32+2×3+m=0,解得m=3.
(2)∵m=3,∴二次函数的表达式为y=-x2+2x+3.
令y=0,得-x2+2x+3=0,
解得x=3或x=-1.
∴点B的坐标为(-1,0).
(3)∵ S△ABD=S△ABC,点D在第一象限,
∴点C,D关于函数图象的对称轴对称.
∵点C为二次函数图象与y轴的交点,∴C(0,3),
又∵该二次函数图象的对称轴为直线x=-2?1×2=1,
∴点D的坐标为(2,3).
?
9.在平面直角坐标系中,抛物线y=2x2+mx+n经过点A(-1,a),B(3,a),且最低点的纵坐标为-4.
(1)求抛物线的函数表达式及a的值;
(2)设抛物线的顶点C关于y轴的对称点为点D,点P是抛物线对称轴上一动点,记抛物线在点A,B之间的部分为图象G(包含A,B两点).若直线DP与图象G恰有两个公共点,结合函数图象,求点P的纵坐标t的取值范围.
答案
9.【解析】 (1)∵抛物线y=2x2+mx+n经过点A(-1,a),B(3,a),∴抛物线的对称轴为直线x=1.
∵抛物线最低点的纵坐标为-4,
∴抛物线的顶点是(1,-4),
∴抛物线的函数表达式是y=2(x-1)2-4,
即y=2x2-4x-2.
把x=-1,y=a代入抛物线的函数表达式,解得a=4.?
(2)∵抛物线的顶点C(1,-4)关于y轴的对称点为点D,
∴D(-1,-4),
∴直线CD的函数表达式为y=-4,
由B(3,4),D(-1,-4),可得直线BD的函数表达式为y=2x-2,
当x=1时,y=0.
结合图象(如图所示),可得-4
表达式
课时1 已知图象上两点求二次函数的表达式
课时1
1.已知抛物线y=ax2+bx-2(a≠0)经过点A(-1,-2),B(1,0),则这个二次函数的表达式为 ( )
A.y=x2+x-2 B.y=-x2+x-2
C.y=x2-x-2 D.y=-x2-x-2
答案
1.A 【解析】 将点A(-1,-2),B(1,0)代入二次函数的表达式,得??????????2=?2,????+?????2=0,解得????=1,????=1,所以这个二次函数的表达式为y=x2+x-2.故选A.
?
知识点1 已知二次函数y=ax2+bx+c的某项系数或常数项求其表达式
2.二次函数y=x2+bx+c中,y与自变量x的部分对应值如表所示,则m的值为 .?
答案
2.-1 【解析】 由题意,得????=?1,1+????+????=?2,解得????=?2,????=?1,所以y=x2-2x-1,把x=2代入,得m=4-4-1=-1.
?
知识点1 已知二次函数y=ax2+bx+c的某项系数或常数项求其表达式
x
?
-2
-1
0
1
2
?
y
?
7
2
-1
-2
m
?
3.[2020河南南阳期末]已知二次函数y=ax2-3x+c的图象经过点(2,0)和(0,4).
(1)求该二次函数的表达式;
(2)画出该函数的图象.
知识点1 已知二次函数y=ax2+bx+c的某项系数或常数项求其表达式
答案
3.【解析】 (1)∵二次函数y=ax2-3x+c的图象经过点(2,0)和(0,4),
∴4?????6+????=0,????=4,解得????=12,????=4,
∴该二次函数的表达式为y=12x2-3x+4.
(2)图象如图所示:
?
知识点1 已知二次函数y=ax2+bx+c的某项系数或常数项求其表达式
4.[2020山东泰安期中]已知抛物线l与抛物线y=-3x2+2x-5的形状和开口方向均相同,且过点A(1,2),B(4,5).
(1)求抛物线l的表达式;
(2)用配方法求抛物线l的对称轴与顶点坐标.
答案
4.【解析】 (1)∵抛物线l与抛物线y=-3x2+2x-5的形状和开口方向均相同,
∴可设抛物线l的表达式为y=-3x2+bx+c,
∵抛物线l过点A(1,2),B(4,5),
∴?3+????+????=2,?3×42+4????+????=5,解得????=16,????=?11,
∴抛物线l的表达式为y=-3x2+16x-11.
(2)y=-3x2+16x-11=-3(x2-163x+649?649)-11=-3(x-83)2+313.
∴抛物线l的对称轴为x=83,顶点坐标为(83,313).
?
知识点1 已知二次函数y=ax2+bx+c的某项系数或常数项求其表达式
5.[2019甘肃庆阳期末]抛物线的顶点坐标为M(-2,1),且经过原点,则该抛物线对应的函数表达式为 ( )
A.y=(x-2)2+1 B.y=-14(x+2)2+1
C.y=(x+2)2+1 D.y=14(x+2)2+1
?
答案
5.B 【解析】 根据题意,设抛物线对应的函数表达式为y=a(x+2)2+1,将(0,0)代入,得4a+1=0,解得a=-14,所以y=-14(x+
2)2+1.故选B.
?
知识点2 用“顶点式”求二次函数的表达式
6.当x=1时,某二次函数取得最大值5,且该二次函数的图象与y轴交于点(0,2),则其表达式为 .?
答案
6.y=-3x2+6x+2 【解析】 由题意设该二次函数的表达式为y=a(x-1)2+5,∵该二次函数的图象与y轴交于点(0,2),∴将(0,2)代入函数表达式得2=a+5,∴a=-3,∴所求的二次函数的表达式为y=-3(x-1)2+5,即y=-3x2+6x+2.
知识点2 用“顶点式”求二次函数的表达式
7.已知抛物线的顶点坐标为(-2,3),开口方向与抛物线y=12x2相反,开口大小与抛物线y=13x2相同,则该抛物线对应的函数表达式为 .?
?
答案
7.y=-13x2-43x+53 【解析】 因为所求抛物线的顶点坐标为(-2,3),所以可设其对应的函数表达式为y=a(x+2)2+3,又因为所求抛物线开口方向与抛物线y=12x2相反,开口大小与抛物线y=13x2相同,所以a=-13,因此所求抛物线对应的函数表达式为y=-13(x+2)2+3=-13x2-43x+53.
?
知识点2 用“顶点式”求二次函数的表达式
8.已知二次函数图象的顶点坐标为(3,5),且抛物线经过点A(1,3).
(1)求此抛物线的表达式;
(2)如果点A关于抛物线的对称轴的对称点是点B,且抛物线与y轴的交点为点C,求△ABC的面积.
答案
8.【解析】 (1)由题意,可设抛物线的表达式为y=a(x-3)2+5,
将点A(1,3)代入,得4a+5=3,解得a=-12,
∴抛物线的表达式为y=-12(x-3)2+5.
(2)∵A(1,3),点A与点B关于对称轴x=3对称,
∴B(5,3),AB=4.
∵当x=0时,y=12,∴C(0,12),
∴S△ABC=12×4×(3-12)=5.
?
知识点2 用“顶点式”求二次函数的表达式
1.[2019河北沧州期末]已知二次函数的部分图象如图所示,对称轴是直线x=-1,则这个二次函数的表达式为 ( )?
A.y=-x2+2x+3 B.y=x2+2x+3
C.y=-x2+2x-3 D.y=-x2-2x+3
答案
1.D 【解析】 由题意知,抛物线的对称轴为直线x=-1,过点(-3,0),(0,3),设抛物线的表达式为y=a(x+1)2+k,将(-3,0),
(0,3)代入,得4????+????=0,????+????=3,解得????=?1,????=4,则抛物线的表达式为y=-(x+1)2+4=-x2-2x+3.故选D.
?
2.[2020浙江杭州拱墅区期末]已知二次函数y=x2+bx+c的图象经过点(2,4),且其顶点在直线y=2x+1上,则它的表达式为 ( )
A.y=x2-x+2 B.y=x2-x+3
C.y=x2-x+5 D.y=x2-2x+4
答案
2.D 【解析】 将(2,4)代入y=x2+bx+c,得4+2b+c=4,得c=-2b,所以二次函数的表达式为y=x2+bx-2b=(x+????2)2-????24-2b,顶点坐标为(-????2,-????24-2b),代入直线y=2x+1,得-b+1=-????24-2b,整理得b2+4b+4=0,解得b=-2,所以c=4,所以表达式为y=x2-2x+4.故选D.
?
3.已知二次函数y=ax2+bx+c的图象是由y=12x2的图象经过平移得到的,若图象与x轴交于点A,C(-1,0),与y轴交于点D(0,52),顶点为点B,则四边形ABCD的面积为 ( )
A.9 B.10 C.11 D.12
?
答案
3.A 【解析】 ∵y=ax2+bx+c的图象是由y=12x2的图象经过平移得到的,∴a=12,∴y=12x2+bx+c.
∵抛物线过点C(-1,0),D(0,52),∴12-b+c=0,c=52,∴b=3,∴ y=12x2+3x+52,∴-????2????=-3,4?????????????24????=-2,∴顶点B的坐标为(-3,-2).∵抛物线的对称轴为直线x=-3,C(-1,0),∴A点坐标为(-5,0),∴AC=4.如图,
S四边形ABCD=S△ACB+S△ACD=12×4×2+12×4×52=9.故选A.
?
4.已知抛物线y=ax2+bx+c经过点A(1,4),B(-2,1),且对称轴为直线x=-1,则当y随x的增大而增大时,x的取值范围为 .?
答案
4.x>-1 【解析】 根据题意,设y=a(x+1)2+k,将点A(1,4),B(-2,1)代入,得4????+????=4,????+????=1,解得????=1,????=0,所以抛物线的表达式为y=(x+1)2,可知当x>-1时,y随x的增大而增大.
?
5.易错题 [2020湖北武汉模拟]已知抛物线经过原点O,还经过点A(2,m),B(4,m).若△AOB的面积为4,则抛物线的表达式为 .?
答案
5.y=-12x2+3x或y=12x2-3x 【解析】 ∵抛物线经过点A(2,m),B(4,m),∴抛物线的对称轴是直线x=3,AB=2.∵△AOB的面积为4,∴12AB·|m|=4,∴m=±4.当m=4时,A(2,4),B(4,4).设抛物线的表达式为y=a(x-3)2+h,把(0,0)和(2,4)代入得9????+h=0,????+h=4,解得????=?12,h=92, ∴抛物线的表达式为y=-12(x-3)2+92,即y=-12x2+3x.当m=-4时,A(2,-4),B(4,-4),设抛物线的表达式为y=k(x-3)2+n,把(0,0)和(2,-4)代入得9????+????=0,????+????=?4,解得????=12,????=?92, ∴抛物线的表达式为y=12(x-3)2-92=12x2-3x.综上所述,抛物线的表达式为y=-12x2+3x或y=12x2-3x.
?
6.如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点E.
(1)求此抛物线对应的函数表达式;
(2)若直线y=x+1与该抛物线交于A,D两点,与y轴交于点F,连接DE,求△DEF的面积.
答案
6.【解析】 (1)∵抛物线y=x2+bx+c与x轴交于点 A(-1,0),B(3,0),
∴1?????+????=0,9+3????+????=0,解得????=?2,????=?3,
故此抛物线对应的函数表达式为y=x2-2x-3.
(2)由????=????+1,????=????2?2?????3,解得????1=?1,????1=0或????2=4,????2=5,
∴D(4,5).
对于直线y=x+1,令x=0,得y=1,∴F(0,1).
对于抛物线y=x2-2x-3,令x=0,得y=-3,
∴E(0,-3),∴EF=4,
∴S△DEF=12EF×4=12×4×4=8.
?
7.[2020江苏苏州期末]如图,在平面直角坐标系中,二次函数y=ax2+bx+6(a≠0)的图象经过点(4,6),与x轴交于A,B(6,0)两点,与y轴交于点C.
(1)求a,b的值;
(2)若点P为直线BC上一点,点P到A,B两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点P,求新抛物线的顶点坐标.
答案
7.【解析】 (1)∵二次函数y=ax2+bx+6(a≠0)的图象经过点(4,6),与x轴交于A,B(6,0)两点,
∴16????+4????+6=6,36????+6????+6=0,解得????=?12,????=2.
?
答案
(2)∵y=-12x2+2x+6=-12(x-2)2+8,
∴抛物线的对称轴为直线x=2,点C的坐标为(0,6).
∵点P到A,B两点的距离相等,
∴点P在抛物线的对称轴x=2上.
∵点B的坐标为(6,0),点C的坐标为(0,6),
∴直线BC的表达式为y=-x+6.
令x=2,则y=-2+6=4, ∴点P的坐标为(2,4).
设平移后的新抛物线的表达式为y=-12(x-h)2+8.
∵新抛物线经过点P,∴4=-12(2-h)2+8,
解得h1=2+22,h2=2-22,
∴新抛物线的顶点坐标为(2+22,8)或(2-22,8).
?
课时2 已知图象上三点求二次函数的表达式
课时2
1.已知二次函数的图象经过点(-1,-9),(1,-3)和(3,-5)三点,则该函数的表达式为( )
A.y=x2+3x-5 B.y=-x2+3x-5
C.y=x2-3x+5 D.y=-x2-3x+5
答案
1.B 【解析】 设二次函数的表达式为y=ax2+bx+c,则?????????+????=?9,????+????+????=?3,9????+3????+????=?5,解得????=?1,????=3,????=?5,所以此二次函数的表达式为y=-x2+3x-5.故选B.
?
知识点1 用“一般式”求二次函数的表达式
2.二次函数y=ax2+bx+c(a,b,c均为常数且a≠0)中的x与y的部分对应值如表所示:
给出下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小;③当x=2时,y=5;④x=3是方程ax2+(b-1)x+c=0的一个根.其中正确的有 .(填序号)?
答案
2.①③④ 【解析】 由x=0时y=3可知c=3,将(-1,-1),(1,5)代入,得?????????+3=?1,????+????+3=5,∴????=?1,????=3,∴二次函数的表达式为y=-x2+3x+3,ac=-3<0,①正确;∵y=-x2+3x+3=-(x-32)2+214,∴当x>32时,y的值随x值的增大而减小,②不正确;当x=2时,y=-4+
6+3=5,③正确;方程ax2+(b-1)x+c=0,即-x2+2x+3=0,解得x=-1或3,④正确.故正确的有①③④.
?
知识点1 用“一般式”求二次函数的表达式
x
?
-1
0
1
?
y
?
-1
3
5
?
3.有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴是y轴.
乙:与x轴有两个交点,其中一个交点的横坐标为1.
丙:与y轴交点的纵坐标是个正数,且以与坐标轴的三个交点为顶点的三角形面积为3.
请写出满足上述全部特点的二次函数的表达式为 .?
答案
3.y=-3x2+3 【解析】 设该二次函数的表达式为y=ax2+bx+c.∵抛物线的对称轴是y轴,∴该二次函数的表达式为y=ax2+c.∵该二次函数的图象与x轴有两个交点,其中一个交点的横坐标为1,∴a+c=0,另一个交点的横坐标为-1.∵该二次函数与y轴交点的纵坐标是个正数,且以三个交点为顶点的三角形面积为3,∴c>0,12×[1-(-1)]×c=3,解得c=3,∴a=
-3.∴满足甲、乙、丙三位同学说的全部特点的二次函数的表达式为y=-3x2+3.
?
知识点1 用“一般式”求二次函数的表达式
4.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表所示.
(1)求该二次函数的表达式;
(2)当x为何值时,y有最小值?最小值是多少?
(3)若点A(m,y1),B(m+1,y2)都在该函数的图象上,试比较y1与y2的大小.
知识点1 用“一般式”求二次函数的表达式
x
?
-1
0
1
2
?
y
?
10
5
2
1
?
答案
4.【解析】 (1)由题表中数据,知当x=-1时,y=10;当x=0时,y=5;当x=1时,y=2.
∴?????????+????=10,????=5,????+????+????=2,解得????=1,????=?4,????=5,
∴该二次函数的表达式为y=x2-4x+5.
(2)由(1)知y=x2-4x+5=(x-2)2+1,
∴当x=2时,y有最小值,最小值是1.
(3)∵点A(m,y1),B(m+1,y2)都在函数y=x2-4x+5的图象上,
∴y1=m2-4m+5,y2=(m+1)2-4(m+1)+5=m2-2m+2,
∴y2-y1=(m2-2m+2)-(m2-4m+5)=2m-3,
∴①当2m-3<0,即m<32时,y1>y2;
②当2m-3=0,即m=32时,y1=y2;
③当2m-3>0,即m>32时,y1
知识点1 用“一般式”求二次函数的表达式
5.已知二次函数的图象如图所示,则该二次函数的表达式为 ( )
A.y=13x2+23x+1
B.y=13x2+23x-1
C.y=13x2-23x+1
D.y=13x2-23x-1
?
答案
5.D 【解析】 设抛物线的表达式为y=a(x+1)(x-3),将点(0,-1)代入,得-3a=-1,解得a=13,所以y=13(x+1)(x-3)=13x2-23x-1.故选D.
?
知识点2 用“交点式”求二次函数的表达式
6.易错题 已知抛物线过点A(-1,0)和点B(3,0),与y轴交于点C,且BC=32,则这条抛物线的表达式为 ( )
A.y=-x2+2x+3
B.y=x2-2x-3
C.y=-x2+2x+3或y=x2-2x-3
D.y=x2+2x-3或y=-x2+2x+3
?
答案
6.C 【解析】 设原点为O,因为BC=32,OB=3,所以点C的坐标有两种可能:C1(0,3),C2(0,-3).设所求抛物线的表达式为y=a(x+1)(x-3),将C1(0,3)代入,得a=-1;将C2(0,-3)代入,得a=1.所以所求抛物线的表达式为y=-x2+2x+3或y=x2-2x-3.故选C.
?
知识点2 用“交点式”求二次函数的表达式
7.已知抛物线y=ax2+bx+c的开口大小与开口方向均与抛物线y=-3x2+1相同,且与x轴相交于点(-2,0),(1,0),则该抛物线的表达式为 . ?
答案
7.y=-3x2-3x+6 【解析】 由题意可得a=-3.因为抛物线与x轴相交于点(-2,0),(1,0),所以抛物线的表达式为y=-3(x+
2)(x-1)=-3x2-3x+6.
知识点2 用“交点式”求二次函数的表达式
8.已知二次函数的图象与x轴的交点为(-5,0),(2,0),且经过点(3,-4),求此二次函数的表达式.
答案
8.【解析】 因为二次函数的图象与x轴的交点为(-5,0),(2,0),
所以设二次函数的表达式为y=a(x+5)(x-2),
又因为图象经过点(3,-4),
所以-4=a×8×1,解得a=-12.
所以此二次函数的表达式为y=-12(x+5)(x-2),
即y=-12x2-32x+5.
?
知识点2 用“交点式”求二次函数的表达式
9.如图,在平面直角坐标系中,已知直线y=-12x+4与y轴交于点A,与x轴交于点B,点C的坐标为(-2,0).
(1)求经过A,B,C三点的抛物线的表达式;
(2)如果M为抛物线的顶点,连接AM,BM,求四边形AOBM的面积.
?
知识点2 用“交点式”求二次函数的表达式
答案
9.【解析】 (1)对于y=-12x+4,当x=0时,y=4,∴A(0,4).
当y=0时,-12x+4=0,解得x=8,∴B(8,0).
设抛物线的表达式为y=a(x+2)(x-8),
将点A(0,4)代入,得-16a=4,解得a=-14,
∴y=-14(x+2)(x-8)=-14x2+32x+4.
(2)∵y=-14x2+32x+4=-14(x-3)2+254,∴M(3,254).
如图,过点M作MD⊥x轴于点D,则MD=254,OD=3,
∴S四边形AOBM=S梯形AODM+S△BDM=12×(4+254)×3+12×(8-3)×254=31.
?
知识点2 用“交点式”求二次函数的表达式
专项3 二次函数的存在性
问题
1.[2020山东潍坊一模]如图,抛物线y=ax2+bx+c与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的函数表达式.
(2)直线BC上方的抛物线上是否存在一点F,使四边形ABFC的面积为17?若存在,求出点F的坐标;若不存在,请说明理由.
答案
1.【解析】 (1)∵A(-2,0)与点B关于对称轴x=1对称,∴B(4,0).
设抛物线的函数表达式为y=a(x+2)(x-4),
∵C(0,4)在y=a(x+2)(x-4)的图象上,
∴4=a×2×(-4),∴a=-12,
∴y=-12(x+2)(x-4)=-12(x2-2x-8)=-12x2+x+4.
?
答案
(2)不存在.理由如下:
假设存在满足条件的点F,如图,连接OF.
∵A(-2,0),B(4,0),C(0,4),∴OA=2,OC=4,OB=4.
设点F(t,-12t2+t+4),其中0
若-t2+4t+12=17,则t2-4t=-5,
∴t2-4t+4=-5+4,∴(t-2)2=-1<0,
∴方程-t2+4t+12=17无解.
故不存在满足条件的点F.
?
2.如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C.
(1)求该抛物线的表达式.
(2)在y轴上是否存在一点P,使△PBO与△AOC相似?若存在,写出点P的坐标;若不存在,请说明理由.
(3)在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
答案
2.【解析】 (1)将点A(1,0),B(-3,0)代入抛物线y=-x2+bx+c,得?1+????+????=0,?9?3????+????=0,解得????=?2,????=3,
∴该抛物线的表达式为y=-x2-2x+3.
(2)存在.
当x=0时,y=3,∴C(0,3),
∴AO=1,BO=3,CO=3.
∵点P在y轴上,∴∠BOP=∠AOC=90°,
∴△PBO与△AOC相似分两种情况.
①当△POB∽△COA时,????????????????=????????????????,
解得PO=9,
∴点P的坐标为(0,9)或(0,-9).
?
答案
②当△POB∽△AOC时,????????????????=????????????????,
解得PO=1,
∴点P的坐标为(0,1)或(0,-1).
∴满足题意的点P的坐标为(0,1),(0,-1),(0,9),(0,-9).
(3)存在.
由题知A,B两点关于抛物线的对称轴x=-1对称,
∴直线BC与x=-1的交点即所求点Q,此时△AQC周长最小.
设直线BC的表达式为y=mx+n,
∴?3????+????=0,????=3,解得????=1,????=3,
∴直线BC的表达式为y=x+3,
当x=-1时,y=2,
∴Q(-1,2).
?
3.[2020广西钦州三模]如图是将抛物线y=-x2平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C.
(1)求该抛物线的函数表达式;
(2)若点N为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=32x+32的图象上一点,若四边形OAPQ为平行四边形,这样的点P,Q是否存在?若存在,分别求出点P,Q的坐标;若不存在,说明理由.
?
答案
3.【解析】 (1)设抛物线的函数表达式是y=-(x-1)2+k.
把A(-1,0)代入,得0=-(-1-1)2+k,解得k=4,
∴抛物线的函数表达式是y=-(x-1)2+4,即y=-x2+2x+3.
(2)在y=-x2+2x+3中,令x=0,则y=3,
∴点C的坐标是(0,3),OC=3.
易知点B的坐标是(3,0),∴OB=3,
∴OC=OB,则△OBC是等腰直角三角形,∴∠OCB=45°.
由题意知,点N在y轴的右侧.如图,过点N作NH⊥y轴,垂足为点H.
∵∠NCB=90°,∴∠NCH=45°,∴NH=CH,
∴HO=OC+CH=3+CH=3+NH.
设点N的坐标是(a,-a2+2a+3),
∴a+3=-a2+2a+3,解得a=0(舍去)或a=1,
∴-a2+2a+3=4,
∴点N的坐标是(1,4).
答案
(3)存在.
如图,∵四边形OAPQ是平行四边形,∴PQ=OA=1,且PQ∥OA,
设P(t,-t2+2t+3),则Q(t+1,-t2+2t+3),
将Q(t+1,-t2+2t+3)代入y=32x+32,得-t2+2t+3=32(t+1)+32,
解得t=0或t=12,∴-t2+2t+3的值为3或154,
∴存在这样的点P,Q,且点P,Q的坐标分别是(0,3),(1,3)或(12,154),(32,154).
?
4.[2019江苏盐城中考]如图所示,二次函数y=k(x-1)2+2的图象与一次函数y=kx-k+2的图象交于A,B两点,点B在点A的右侧,直线AB分别与x轴,y轴交于C,D两点,其中k<0.
(1)求A,B两点的横坐标;
(2)若△OAB是以OA为腰的等腰三角形,求k的值;
(3)二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.
答案
4.【解析】 (1)联立两函数的表达式为????=????(?????1)2+2,????=?????????????+2,
解得????=1,????=2或????=2,????=????+2.
∵点B在点A的右侧,
∴点A,B的横坐标分别为1,2.
(2)由(1)知点A的坐标为(1,2),点B的坐标为(2,k+2),
故OA2=12+22=5,OB2=22+(k+2)2=k2+4k+8,AB2=(2-1)2+(2-k-2)2=k2+1.
①当OA=OB时,k2+4k+8=5,
解得k1=-1,k2=-3.
②当OA=AB时,k2+1=5,
解得k3=-2,k4=2(不符合题意,舍去),
综上所述,k的值为-1,-2或-3.
?
答案
(3)存在,k的值为-3或?4?73.
解法一 ①当点B在x轴上方时,k+2>0,即-2
∵BF⊥AE,AE⊥x轴,
∴BF∥x轴,
∴∠FBE=∠BEC.
∵∠GBF=∠FBE,
∴∠GBE=∠GBF+∠FBE=2∠BEC.
∵AE∥y轴,
∴∠BAE=∠ODC.
∵∠ODC=2∠BEC,
∴∠BAE=2∠BEC,
∴∠BAE=∠GBE.
?
答案
又∵∠GEB=∠BEA,
∴△EBG∽△EAB,
∴????????????????=????????????????,即EB2=EG·EA.
∵A(1,2),B(2,k+2),
∴E(1,0),F(1,k+2).
∵GE=2EF=2k+4,BE2=12+(k+2)2=k2+4k+5,EA=2,
∴k2+4k+5=2×(2k+4),解得k1=-3,k2=3(不符合题意,舍去).
②当点B在x轴下方时,k+2<0,即k<-2.
如图2,过点B作BM⊥直线AE于点M,在线段AM的延长线上找一点N,使∠NBM=∠EBM,则EM=MN.
同①易证△BNE∽△ANB,
∴????????????????=????????????????,即BN2=EN·NA.
?
答案
∵A(1,2),B(2,k+2),
∴E(1,0),M(1,k+2),
∴NE=2EM=-2k-4,BN2=BE2=12+(k+2)2=k2+4k+5,NA=2-(2k+4)=-2k-2,
∴k2+4k+5=(-2k-4)(-2k-2),
解得k3=?4?73,k4=?4+73(不符合题意,舍去),
综上所述,存在实数k,使得∠ODC=2∠BEC,k的值为-3或?4?73.
解法二 由题意得点E的坐标为(1,0).
对于一次函数y=kx-k+2,当y=0时,x=?????2????,即点C的坐标为(?????2????,0).
当x=0时,y=-k+2,即点D的坐标为(0,-k+2),
∴tan∠ODC=????????????????=?????2?????????+2=-1????.
过点B作BP⊥x轴,垂足为P,则EP=2-1=1,BP=|k+2|,
在线段EP上找一点Q,使得QE=QB,则∠BQP=2∠BEC,
?
答案
设QE=QB=m,则PQ=1-m.
在Rt△BQP中,BP2+QP2=BQ2,
∴(k+2)2+(1-m)2=m2,
整理,得2m=k2+4k+5.
∵∠ODC=2∠BEC,
∴tan∠BQP=tan∠ODC=-1????,
∴????????????????=|????+2|1?????=-1????.
①当k+2>0,即-2
②当k+2<0,即k<-2时,
??????21?????=-1????,解得k3=?4?73,k4=?4+73(不符合题意,舍去).
综上所述,存在实数k,使得∠ODC=2∠BEC,k的值为-3或?4?73.
?
易错疑难集训(一)
集训(一)
1.[2020河南洛阳期末]已知二次函数y=mx2+x+m(m-2)的图象经过原点,则m的值为( )
A.0或2 B.0
C.2 D.无法确定
答案
1.C 【解析】 根据题意,得m(m-2)=0,∴m=0或m=2,∵二次函数的二次项系数不为0,∴m=2.故选C.
易错点1 忽略“二次项系数不为0”
2.已知函数y=(1-n)????????2+?????4是关于x的二次函数,当n为何值时,抛物线有最低点?求出这个最低点的坐标,在这种情况下,x为何值时,函数y随x的增大而增大?
?
答案
2.【解析】 因为函数y=(1-n)????????2+?????4是二次函数,
所以????2+?????4=2,1?????≠0,解得n=2或n=-3.
又因为抛物线有最低点,所以1-n>0,解得n<1,所以n=-3.
此时y=4x2,
所以当n=-3时,抛物线有最低点,这个最低点的坐标是(0,0),
在这种情况下,当x>0时,函数y随x的增大而增大.
?
易错点1 忽略“二次项系数不为0”
抛物线有最低点或最高点,是由二次函数y=ax2+bx+c的二次项系数a的符号决定的.当a>0时,抛物线有最低点;当a<0时,抛物线有最高点.本题易误认为当1-n<0时,抛物线有最低点,错误得出n=2.也易误认为当x<0时,函数y随x的增大而增大.
易错点1 忽略“二次项系数不为0”
3.将函数y=x2+x的图象向右平移a(a>0)个单位长度,得到函数y=x2-3x+2的图象,则a的值为 ( )
A.1 B.2
C.3 D.4
答案
3.B 【解析】 将函数y=x2+x的图象向右平移a(a>0)个单位长度,根据二次函数图象的平移规律可得,y=(x-a)2+(x-a),整理得y=x2-(2a-1)x+a2-a,而平移后的函数为y=x2-3x+2,可知-(2a-1)=-3,a2-a=2,所以a=2.故选B.
易错点2 对二次函数图象的平移规则理解不透
4.若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先向右平移1个单位长度,再向上平移3个单位长度,则得到的抛物线的表达式为 ( )
A.y=(x-2)2+3 B.y=(x-2)2+5
C.y=x2-1 D.y=x2+4
答案
4.C 【解析】 将平面直角坐标系xOy先向右平移1个单位长度,再向上平移3个单位长度,相当于把抛物线向左平移1个单位长度,再向下平移3个单位长度.∵y= x2-2x+3=(x-1)2+2,∴得到的抛物线的表达式为y=(x-1+1)2+2-3=x2-1.故选C.
易错点2 对二次函数图象的平移规则理解不透
5.把抛物线y=ax2+bx+c先向右平移3个单位长度,再向下平移2个单位长度,所得的图象的表达式是y=x2-3x+5,则a+b+c= .?
答案
5.11 【解析】 利用逆向思维来解题.因为将抛物线y=ax2+bx+c先向右平移3个单位长度,再向下平移2个单位长度后,得到抛物线y=x2-3x+5,所以将抛物线y=x2-3x+5先向左平移3个单位长度,再向上平移2个单位长度后,可得抛物线y=ax2+
bx+c,所以y=(x+3)2-3(x+3)+5+2=x2+3x+7=ax2+bx+c,令x=1,则a+b+c=11.
易错点2 对二次函数图象的平移规则理解不透
1.当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为 .?
答案
1.2或-3 【解析】 易知二次函数y=-(x-m)2+m2+1的图象的对称轴为直线x=m.①若m<-2,则当x=-2时,y有最大值-4m-3,令-4m-3=4,解得m=-74,与m<-2矛盾,故m值不存在;②若-2≤m≤1,则当x=m时,y有最大值m2+1,令m2+1=4,解得m1=-3,m2=
3(舍去);③若m>1,则当x=1时,y有最大值2m,令2m=4,解得m=2.综上所述,m的值为2或-3.
?
疑难点1 二次函数在自变量范围内的最值问题
本题考查二次函数的最值问题,难点在于分情况讨论.根据对称轴的位置,分三种情况讨论求解即可.
2.如图,一段抛物线y=-x2+4(-2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1,将C1绕点A1旋转180°得到C2,顶点为D2.C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是 ( )?
A.6
2.D 【解析】 翻折后的抛物线的表达式为y=(x-4)2-4=x2-8x+12.∵x1,x2,x3均为正数,∴由题图知,点P1(x1,y1),P2(x2,y2),
P3(x3,y3)在第四象限,∴2≤x3≤4,根据抛物线的对称性可知x1+x2=8,∴10≤x1+x2+x3≤12,即10≤t≤12.故选D.
疑难点2 抛物线的全等变换问题
3.[2020江苏南京期末]已知二次函数y=ax2+bx+c(a≠0),y与自变量x的部分对应值如表所示:
则该二次函数图象关于x轴对称的图象所对应的函数表达式为 .?
答案
3.y=-x2+2x+3 【解析】 解法一 根据题意,知原二次函数图象的顶点坐标为(1,-4),设原二次函数的表达式为y=a(x-1)2-4,把(0,-3)代入y=a(x-1)2-4,得-3=a(0-1)2-4, 解得a=1,所以原二次函数的表达式y=(x-1)2-4.因为原二次函数图象的顶点坐标为(1,-4),所以该点关于x轴对称的点的坐标是(1,4),所以该二次函数图象关于x轴对称的图象所对应的函数表达式是y=-(x-1)2+4=-x2+2x+3.
解法二 根据题意,知原二次函数图象的顶点坐标为(1,-4),该点关于x轴对称的点的坐标是(1,4),设新二次函数的表达式为y=a(x-1)2+4,(0,-3)关于x轴对称的点的坐标是(0,3),把(0,3)代入y=a(x-1)2+4,得3=a(0-1)2+4, 解得a=-1,所以该二次函数图象关于x轴对称的图象所对应的函数表达式是y=-(x-1)2+4=-x2+2x+3.
疑难点2 抛物线的全等变换问题
x
?
-2
-1
0
1
2
?
y
?
5
0
-3
-4
-3
?
4.[2020湖北襄阳樊城区模拟]如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点.动点P在线段OA上,从点O出发,向点A以1个单位长度/s的速度匀速运动;同时,动点Q在线段AB上,从点A出发,向点B以2个单位长度/s的速度匀速运动.连接PQ,设运动时间为t s.
(1)求抛物线的表达式;
(2)当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E;过点Q作QF∥y轴,交抛物线于点F,连接EF.当EF∥PQ时,求点F的坐标.
?
疑难点3 二次函数与动点问题的综合
答案
4.【解析】 (1)由题可知,A(3,0),B(0,3),
将A(3,0),B(0,3)代入y=-x2+bx+c,得
?9+3????+????=0,????=3,解得????=2,????=3,
∴抛物线的表达式为y=-x2+2x+3.
(2)∵OA=OB=3,OA⊥OB,∴∠PAQ=45°.
当运动时间为t s时,AQ=2t,OP=t,AP=3-t.
①当∠AQP=90°时,在Rt△APQ中,cos∠PAQ=????????????????=22,
∴2????3?????=22,解得t=1;
②当∠APQ=90°时,在Rt△APQ中,cos∠PAQ=????????????????=22,
?
疑难点3 二次函数与动点问题的综合
答案
∴3?????2????=22,解得t=32.
综上所述,当t=1或32时,△APQ为直角三角形.
(3)如图,过点Q作QH⊥x轴于点H,
由题意知点P的坐标为(t,0),
则点E的坐标为(t,3-t),EP=3-t.
∵AQ=2t,∴AH=AQcos∠PAQ=t,∴OH=3-t.
将x=3-t代入y=-x+3中,得y=t,∴Q(3-t,t),
将x=3-t代入y=-x2+2x+3中,得y=-(3-t)2+2(3-t)+3=-t2+4t,∴F(3-t,-t2+4t),
∴QF=-t2+4t-t=-t2+3t,
∵PE∥y轴,QF∥y轴,∴PE∥QF,
?
疑难点3 二次函数与动点问题的综合
答案
又∵EF ∥ PQ,∴四边形PQFE是平行四边形,
∴EP=QF,∴3-t=-t2+3t,
解得t1=1,t2=3(舍去),
∴点F的坐标为(2,3).
疑难点3 二次函数与动点问题的综合
4 二次函数的应用
课时1 利用二次函数解决面积最值问题
课时1
1.用一条长为40 cm的绳子围成一个面积为 S cm2 的矩形,则S的值不可能为 ( )
A.20 B.40 C.100 D.120
答案
1.D 【解析】 设所围成矩形的一边长为x cm,则由题意,得S=x(20-x)=-x2+20x,∵-1<0,∴S有最大值,即当 x=-202×(?1)=
10时,S最大=100.∵120>100,∴S的值不可能为120.故选D.
?
知识点 利用二次函数解决面积最值问题
2.如图,在矩形ABCD中,AD=4,点E在边AD上,不与A,D重合,连接CE,以CE为边向右上方作正方形CEFG,过点F作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED.
(2)当AE为何值时,△AEF的面积最大?
知识点 利用二次函数解决面积最值问题
答案
2.【解析】 (1)∵四边形CEFG是正方形,∴CE=EF.
∵∠FEC=∠FEH+∠CED=90°,∠DCE+∠CED=90°,
∴∠FEH=∠DCE.
∵∠FHE=∠D=90°,∴△FEH≌△ECD,
∴FH=ED.
(2)设AE=a(0
∴当AE=2时,△AEF的面积最大.
?
知识点 利用二次函数解决面积最值问题
3.如图,在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A出发沿AB边向点B以1 cm/s的速度运动,同时点Q从点B出发沿BC边向点C以2 cm/s的速度运动,当其中一点运动至终点时,另一点也随之停止运动.
(1)设运动t s后,五边形APQCD的面积为S cm2,写出S与t之间的函数关系式,并指出自变量t的取值范围.
(2)t为何值时,S最小?最小值是多少?
知识点 利用二次函数解决面积最值问题
答案
3.【解析】 (1)t s时,AP=tcm,BQ=2t cm,
故PB=(6-t)cm,
故S△PBQ=12(6-t)·2t=(-t2+6t)(cm2).
∵S矩形ABCD=6×12=72(cm2),
∴S=72-S△PBQ=t2-6t+72.
自变量t的取值范围为0
故当t=3时,S最小,最小值是63.
?
知识点 利用二次函数解决面积最值问题
4.如图,在一面靠墙的空地上,用长24 m的篱笆围成中间隔有两道篱笆的长方形花圃,墙的最大可用长度为8 m,设花圃的一边AB的长为x m,面积为S m2.
(1)求S与x之间的函数关系式.
(2)求自变量x的取值范围.
(3)当x取何值时,所围成的花圃面积最大?最大面积是多少?
知识点 利用二次函数解决面积最值问题
答案
4.【解析】 (1)花圃的一边AB长为x m,则BC长为(24-4x)m,
根据题意,得S与x之间的函数关系式为S=x(24-4x)=-4x2+24x.
(2)∵墙的最大可用长度为8 m,
∴0<24-4x≤8,解得4≤x<6,
即自变量x的取值范围为4≤x<6.
(3)由(1)知S=-4x2+24x=-4(x-3)2+36,
∴当x>3时,S的值随x值的增大而减小.
∵4≤x<6,
∴当x=4时,S取得最大值,且最大值为32,
∴当x取4时,花圃面积最大,最大面积是32 m2.
知识点 利用二次函数解决面积最值问题
5.[2020江苏连云港期末]为了节省材料,某水产养殖户利用水库堤岸(堤岸足够长)为一边,用总长为80 m的围网在水库中围成如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长为x m,矩形区域ABCD的面积为
y m2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围.
(2)x为何值时,y有最大值?最大值是多少?
知识点 利用二次函数解决面积最值问题
答案
5.【解析】 (1)解法一 设AE=a m,
由题意,得AE·AD=2BE·BC,AD=BC,
所以BE=12am,AB=32a m.
由题意,得2x+3a+a=80,
所以a=20-12x,y=AB·BC=32a·x=32(20-12x)x,
即y=-34x2+30x,其中0
DF·x=23y,DF=2????3????,
所以2x+2×????3????+3×2????3????=80,
整理,得y=-34x2+30x,其中0
知识点 利用二次函数解决面积最值问题
答案
(2)由(1)知y=-34x2+30x=-34(x-20)2+300,
因为-34<0,所以抛物线开口向下,
又因为0
知识点 利用二次函数解决面积最值问题
1.[2019浙江绍兴柯桥区期末]在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x.若在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为 ( )
A.193 m2 B.194 m2 C.195 m2 D.196 m2
答案
1.C 【解析】 ∵AB=xm,∴BC=(28-x)m,则S=AB·BC=x(28-x)=-x2+28x.由题意可知????≥6,28?????≥15,解得6≤x≤13.易知当6≤x≤13时,S随x的增大而增大,∴当x=13时,S取得最大值,最大值为195 m2.故选C.
?
2.如图,在△ABC中,∠B=90°,AB=12 cm,BC=24 cm,动点P从点A开始沿边AB向点B以2 cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向点C以4 cm/s的速度移动(不与点C重合).若P,Q分别从A,B同时出发,则经过 s,四边形APQC的面积最小.?
答案
2.3 【解析】 设运动时间为t s,易知0
?
3.如图,在直角三角形AEF内部作矩形ABCD,其中AB和AD分别在两直角边上,点C在斜边上,设矩形的一边AB长为x,矩形的面积为y,则y的最大值为 .?
答案
3.300 【解析】 由题可知,△EDC∽△EAF,CD=AB=x,∴????????????????=????????????????,∴30?????????30=????40,解得AD=30-34x,∴y=AD·AB=(30-34x)·x,即y=-34(x-20)2+300,∴当x=20时,y取得最大值300.
?
4.[2020河北石家庄新华区一模]如图,西游乐园景区内有一块矩形油菜花田地(单位:m),现在其中修建一条观花道(阴影所示),供游人赏花,设修建的观花道的面积为y m2.
(1)求y与x之间的函数关系式;
(2)若修建的观花道的面积为13 m2,求x的值;
(3)若要求0.6≤x≤1,求修建后油菜花地所占面积的最大值.
答案
4.【解析】 (1)y=6×8-2×12×(6-x)(8-x)=-x2+14x(0
∵0
则w=48-y=x2-14x+48=(x-7)2-1,
∴当x<7时,w随x的增大而减小,
又∵0.6≤x≤1,
∴当x=0.6时,w取得最大值,最大值为39.96.
答:修建后油菜花地所占面积的最大值为39.96 m2.
?
5.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3).
(1)求抛物线的函数表达式及顶点D的坐标;
(2)若P为线段BD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAC面积的最大值和此时点P的坐标.
答案
5.【解析】 (1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3),代入y=ax2+bx+c,
得????=3,?????????+????=0,9????+3????+????=0,解得????=?1,????=2,????=3,
∴抛物线的函数表达式为y=-x2+2x+3,
∴抛物线的顶点D的坐标为(1,4).
(2)设直线BD的函数表达式为y=kx+m,
由B(3,0),D(1,4)得3????+????=0,????+????=4,解得????=?2,????=6,
∴直线BD的函数表达式为y=-2x+6.
∵点P在线段BD上,∴设P(p,-2p+6)(1≤p<3),
则OM=p,PM=-2p+6,
又∵OA=1,OC=3,
?
答案
∴四边形PMAC的面积为12×1×3+12×(-2p+6+3)×p=-p2+92p+32=-( p-94)2+10516.
∵1<94<3,
∴当p=94时,四边形PMAC的面积有最大值,最大值为10516,
此时,-2p+6=-2×94+6=32,点P的坐标为(94,32).
?
6.[2019浙江绍兴中考]有一块形状如图所示的五边形余料ABCDE,AB=AE=6,BC=5,∠A=∠B=90°,∠C=135°,∠E>90°.要在这块余料中截取一块矩形材料,其中一条边在AE上,并使所截矩形材料的面积尽可能大.
(1)若所截矩形材料的一条边是BC或AE,求矩形材料的面积.
(2)能否截出比(1)中更大面积的矩形材料?如果能,求出能截取矩形材料面积的最大值;如果不能,说明理由.
答案
6.【解析】 (1)设矩形材料的面积为S.
①若所截矩形材料的一条边是BC,如图1所示.
过点C作CF⊥AE于F,S=AB·BC=6×5=30.
②若所截矩形材料的一条边是AE,如图2所示.
过点E作EF∥AB交CD于F,过点F作FG⊥AB于G,过点C作CH⊥FG于H,
则四边形AEFG为矩形,四边形BCHG为矩形,
∴AE=FG=6,HG=BC=5.
∵∠BCD=135°,∴∠FCH=45°,
∴△CHF为等腰直角三角形,
∴BG=CH=FH=FG-HG=6-5=1,
∴AG=AB-BG=6-1=5,
∴S=AE·AG=6×5=30.
答案
(2)能.
如图3,在CD上取点F,过点F作FM⊥AB于M,FN⊥AE于N,过点C作CG⊥FM于G,
则四边形ANFM为矩形,四边形BCGM为矩形,
∴MG=BC=5,BM=CG.
∵∠BCD=135°,∴∠FCG=45°,
∴△CGF为等腰直角三角形,FG=CG.
设AM=x(0
∴S=AM×FM=x(11-x)=-x2+11x=-(x-5.5)2+30.25,
∴当x=5.5时,S取得最大值,最大值为30.25.
课时2 利用二次函数解决利润最大问题
课时2
1.某鞋帽专卖店销售一种绒帽,若销售这种帽子每天的利润y(元)与销售价格x(元/件)满足关系式y=-x2+70x-800,想要获得最大利润,则销售价格为 ( )
A.30元/件 B.35元/件
C.40元/件 D.45元/件
答案
1.B 【解析】 根据题意得,y=-x2+70x-800=-(x-35)2+425,当x=35时,y有最大值.故选B.
知识点 利用二次函数解决利润最大问题
2.某商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1 558,其中15≤x≤22,那么一周可获得的最大利润是 ( )
A.2
