北师大版九年级下册数学 第二章 二次函数素养拓展+中考真题课件(58张PPT)
文档属性
| 名称 | 北师大版九年级下册数学 第二章 二次函数素养拓展+中考真题课件(58张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 10:00:29 | ||
图片预览







文档简介
第二章 二次函数
数学·九年级下册·北师
函数是反映现实世界中数量关系和变化规律的一种常见数学模型,函数的图象是研究函数性质的重要工具,体现数形结合思想的应用.解决与二次函数图象、性质有关的问题,关键是明确表达式的系数与图象的关系,能将数、形有机结合,相互转化;应用二次函数解决实际问题时,要特别注意自变量取值范围的限制条件.例如,第2题,根据绝对值的几何意义画出函数y=|ax2+bx+c|的图象,结合图象判断方程有两个不相等的实数根的条件,培养学生的分类讨论思想和分析问题、解决问题的能力;第3题,利用根的判别式探究直线与双抛物线的交点问题,关注直观想象.
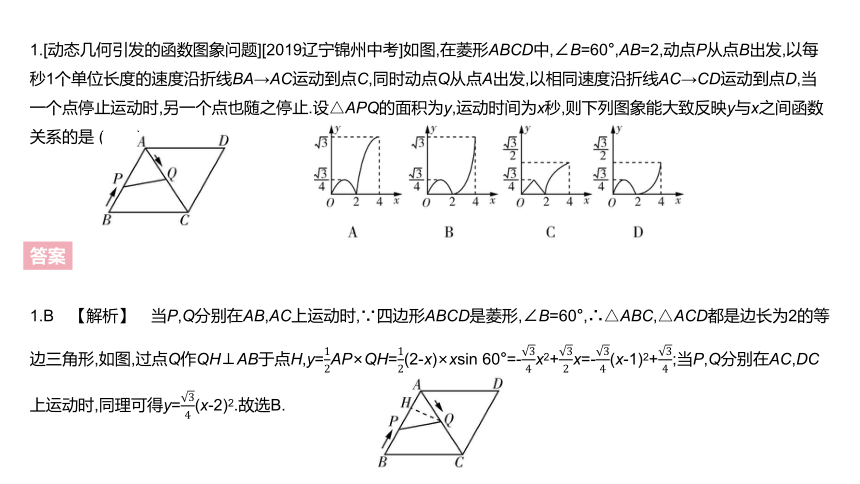
1.[动态几何引发的函数图象问题][2019辽宁锦州中考]如图,在菱形ABCD中,∠B=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD运动到点D,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是 ( )
答案
1.B 【解析】 当P,Q分别在AB,AC上运动时,∵四边形ABCD是菱形,∠B=60°,∴△ABC,△ACD都是边长为2的等边三角形,如图,过点Q作QH⊥AB于点H,y=12AP×QH=12(2-x)×xsin 60°=-34x2+32x=-34(x-1)2+34;当P,Q分别在AC,DC上运动时,同理可得y=34(x-2)2.故选B.
?
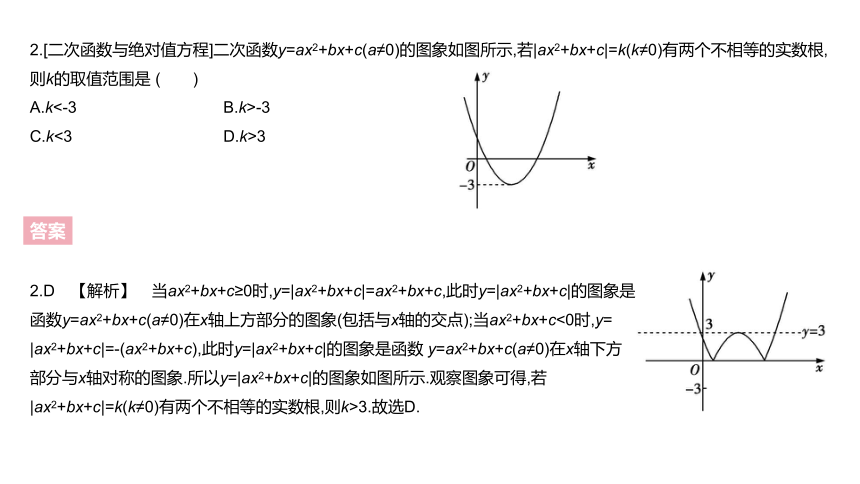
2.[二次函数与绝对值方程]二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是 ( )
A.k<-3 B.k>-3
C.k<3 D.k>3
答案
2.D 【解析】 当ax2+bx+c≥0时,y=|ax2+bx+c|=ax2+bx+c,此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c(a≠0)在x轴上方部分的图象(包括与x轴的交点);当ax2+bx+c<0时,y=
|ax2+bx+c|=-(ax2+bx+c),此时y=|ax2+bx+c|的图象是函数 y=ax2+bx+c(a≠0)在x轴下方部分与x轴对称的图象.所以y=|ax2+bx+c|的图象如图所示.观察图象可得,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k>3.故选D.
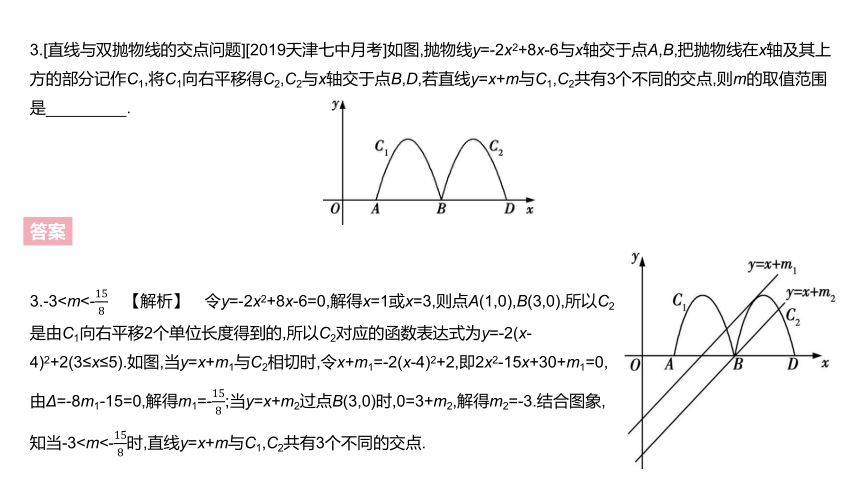
3.[直线与双抛物线的交点问题][2019天津七中月考]如图,抛物线y=-2x2+8x-6与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是 .?
答案
3.-3?
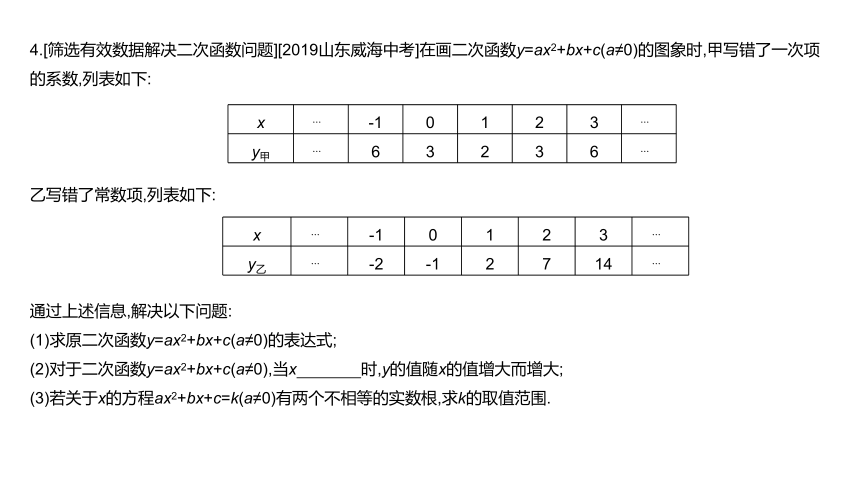
4.[筛选有效数据解决二次函数问题][2019山东威海中考]在画二次函数y=ax2+bx+c(a≠0)的图象时,甲写错了一次项的系数,列表如下:
乙写错了常数项,列表如下:
通过上述信息,解决以下问题:
(1)求原二次函数y=ax2+bx+c(a≠0)的表达式;
(2)对于二次函数y=ax2+bx+c(a≠0),当x 时,y的值随x的值增大而增大;?
(3)若关于x的方程ax2+bx+c=k(a≠0)有两个不相等的实数根,求k的取值范围.
x
?
-1
0
1
2
3
?
y甲
?
6
3
2
3
6
?
x
?
-1
0
1
2
3
?
y乙
?
-2
-1
2
7
14
?
答案
4.【解析】 (1)由甲同学的列表知c=3,由此可将乙同学的列表修正为:
把x=-1,y=2;x=1,y=6代入y=ax2+bx+3,得
?????????+3=2,????+????+3=6,解得????=1,????=2,
∴原二次函数的表达式为y=x2+2x+3.
(2)≥-1
二次函数y=x2+2x+3图象的对称轴为直线x=-22×1=-1,∵抛物线的开口向上,∴当x≥-1时,y的值随x的值增大而增大.
?
x
?
-1
0
1
2
3
?
y乙
?
2
3
6
11
18
?
答案
(3)解法一 关于x的方程ax2+bx+c=k(a≠0)有两个不相等的实数根,
即x2+2x+3-k=0有两个不相等的实数根,
∴Δ=4-4(3-k)>0,解得k>2.
解法二 由关于x的方程ax2+bx+c=k(a≠0)有两个不相等的实数根,得直线y=k与抛物线y=x2+2x+3有两个交点.
∵抛物线y=x2+2x+3的顶点坐标为(-1,2),且开口向上,
∴k的取值范围为k>2.
答案
1.B 【解析】 y=-x2+4x+3=-(x-2)2+7,所以该抛物线的顶点坐标是(2,7).故选B.
一、选择题
1.[2020福建莆田秀屿区期中]抛物线y=-x2+4x+3的顶点坐标为 ( )
A.(-2,7) B.(2,7)
C.(2,-9) D.(-2,-9)
答案
2.B 【解析】 ∵抛物线y=-x2+bx+4经过(-2,n)和(4,n)两点,∴抛物线的对称轴为直线x=1,∴????2=1,解得b=2,∴y=-x2+
2x+4.将(-2,n)代入y=-x2+2x+4,得n=-4.故选B.
?
2.[2019河南中考]已知抛物线y=-x2+bx+4经过(-2,n)和(4,n)两点,则n的值为 ( )
A.-2 B.-4 C.2 D.4
答案
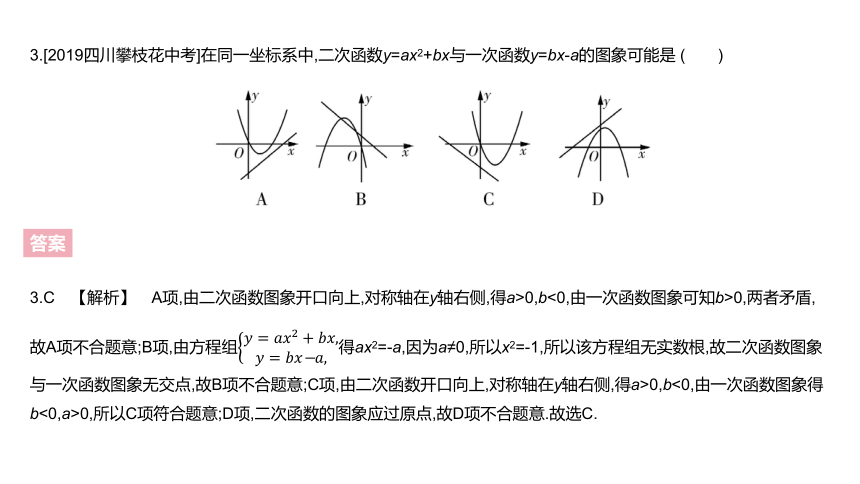
3.C 【解析】 A项,由二次函数图象开口向上,对称轴在y轴右侧,得a>0,b<0,由一次函数图象可知b>0,两者矛盾,故A项不合题意;B项,由方程组????=????????2+????????,????=?????????????,得ax2=-a,因为a≠0,所以x2=-1,所以该方程组无实数根,故二次函数图象与一次函数图象无交点,故B项不合题意;C项,由二次函数开口向上,对称轴在y轴右侧,得a>0,b<0,由一次函数图象得b<0,a>0,所以C项符合题意;D项,二次函数的图象应过原点,故D项不合题意.故选C.
?
3.[2019四川攀枝花中考]在同一坐标系中,二次函数y=ax2+bx与一次函数y=bx-a的图象可能是 ( )
答案
4.C 【解析】 抛物线y=x2+(m+1)x+m的开口向上,对称轴为直线x=-????+12.因为当x=1时,y>0,所以12+m+1+m>0,解得m>-1.因为当x<-2时, y随x的增大而减小,所以-????+12≥-2,解得m≤3.故m的取值范围为-1?
4.已知抛物线y=x2+(m+1)x+m,当x=1时,y>0,且当x<-2时, y随x的增大而减小,则m的取值范围是 ( )
A.m>-1 B.m<3
C.-1答案
5.D 【解析】 一元二次方程ax2+bx+c+7=0的根是抛物线y=ax2+bx+c与直线y=-7的交点的横坐标.由题中表格,可知抛物线y=ax2+bx+c与直线y=-7的一个交点为(3,-7).因为当x=-2和x=0时,函数值都是4,所以抛物线y=ax2+bx+c的对称轴是直线x=-1.根据抛物线的对称性,可知抛物线y=ax2+bx+c与直线y=-7的另一个交点坐标为(-5,-7),所以一元二次方程ax2+bx+c+7=0的根是x1=-5,x2=3.故选D.
5.已知二次函数y=ax2+bx+c(a≠0),下表列出了该函数x,y的部分对应值,则一元二次方程ax2+bx+c+7=0的根是 ( )
A.x1=2,x2=-3 B.x1=-5,x2=-3
C.x1=-4,x2=3 D.x1=-5,x2=3
x
?
-2
-1
0
1
2
3
?
y
?
4
5
4
2
-1
-7
?
答案
6.B 【解析】 因为抛物线的顶点A的坐标为(-3,0),所以可设B(-3-m,2)(m>0),则C(-3+m,2),所以BC=2m.因为△ABC为等边三角形,所以AC=2m,所以m2+22=(2m)2,所以m=233,所以C(-3+233,2).设抛物线的表达式为y=a(x+3)2,将点C的坐标代入,得a(-3+233+3)2=2,解得a=32,所以y=32(x+3)2,当x=0时,y=272,所以此抛物线与y轴的交点坐标为(0,272).故选B.
?
6.如图,平面直角坐标系内有一顶点为A的抛物线,此抛物线与直线y=2交于B,C两点,△ABC为等边三角形.若点A的坐标为(-3,0),则此抛物线与y轴的交点坐标为 ( )
A.(0,92) B.(0,272) C.(0,9) D.(0,19)
?
答案
7.A 【解析】 如图,以A为坐标原点,AE所在直线为x轴,AB所在直线为y轴,建立平面直角坐标系.根据题意知,抛物线的顶点C的坐标为(1.6,2.5),设抛物线的表达式为y=a(x-1.6)2+2.5,将点B(0,1.5)代入,得2.56a+2.5=1.5,解得a=-12.56,所以抛物线的表达式为y=-12.56(x-1.6)2+2.5.当y=1.86时,-12.56(x-1.6)2+2.5=1.86,解得x1=0.32(舍去),x2=2.88.所以茶几到灯柱的距离AE为2.88 m.故选A.
?
7.[2020河北衡水模拟]如图是一款抛物线型落地灯筒示意图,灯柱AB的高为1.5 m,防滑螺母C为抛物线支架的最高点,距灯柱的水平距离为1.6 m,灯罩D距离地面1.86 m,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为 ( )?
A.2.88 m B.3.2 m C.2.5 m D.1.6 m
8.[2019四川达州中考]如图,边长都为4的正方形ABCD和正三角形EFG如图放置,AB与EF在一条直线上,点A与点F重合.现将△EFG沿AB方向以每秒1个单位长度的速度匀速运动,当点F与B重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是 ( )
答案
8.C 【解析】 当0≤t≤2时,如图1,设GF与AD交于点M,AF=t,AM=AF·tan 60°=3t,所以S=12AF·AM=32t2,即S与t是二次函数关系,其图象开口向上,有最小值0.当2?
答案
9.3 【解析】 设平移后的抛物线为y=(x-3+a)2-2(a>0),因为该抛物线经过点A(2,2),所以2=(2-3+a)2-2,解得a=3或a=
-1(舍去),故将抛物线y=(x-3)2-2向左平移3个单位长度后经过点A(2,2).
二、填空题
9.[2019四川凉山州中考]将抛物线y=(x-3)2-2向左平移 个单位长度后经过点A(2,2).?
答案
10.-2 【解析】 设OA,BC交于点D.∵四边形ABOC是正方形,∴BC⊥OA,OD=BD,∴点B的坐标为(-????2????,-????2????).∵抛物线y=ax2过点B,∴-????2????=a(-????2????)2,解得b1=0(舍去),b2=-2.
?
10.如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx(a>0)的顶点为C,与x轴的正半轴交于点A,它的对称轴与抛物线y=ax2(a>0)交于点B.若四边形ABOC是正方形,则b的值是 .?
答案
11.2 【解析】 ∵y=ax2-2ax+83=a(x-1)2-a+83(a>0),且抛物线与y轴交于点A,∴A的坐标为(0,83),抛物线的对称轴为x=1,顶点P的坐标为(1,83-a),∴点M的坐标为(2,83).∵点M为线段AB的中点,∴点B的坐标为(4,83).设直线OP的函数表达式为y=kx(k为常数,且k≠0),将点B(4,83)代入,得83=4k,解得k=23,即直线OP的函数表达式为y=23x.将点P(1, 83-a)代入y=23x,得83-a=23,解得a=2.
?
11.[2019吉林长春中考]如图,在平面直角坐标系中,抛物线y=ax2-2ax+83(a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M,P为抛物线的顶点.若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为 .?
?
答案
12.3 【解析】 ∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=-????2????=1,∴b=-2a>0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc<0,故①正确;由图象的对称性知,当x=2时,y>0,即4a+2b+c>0,∴a+12b+14c>0,故②正确;∵点C的坐标为(0,c),OA=OC,∴点A的坐标为(-c,0),把A(-c,0)代入y=ax2+bx+c,得ac2-bc+c=0,∴ac-b+1=0,故③错误;∵点A的坐标为
(-c,0),对称轴为直线x=1,∴点B的坐标为(2+c,0),∴2+c是关于x的一元二次方程ax2+bx+c=0的一个根,故④正确.综上所述,①②④正确,有3个.
?
12.[2020湖北随州模拟]如图,已知二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,OA=OC,对称轴为直线x=1,给出下列结论:①abc<0;②a+12b+14c>0;③ac+b+1=0;④2+c是关于x的一元二次方程ax2+bx+c=0的一个根.其中正确的结论有 个.?
?
三、解答题
13.[2019安徽中考]一次函数y=kx+4与二次函数y=ax2+c的图象的一个交点的坐标为(1,2),另一个交点是该二次函数图象的顶点.
(1)求k,a,c的值;
(2)过点A(0,m)(0答案
13.【解析】 (1)把(1,2)代入y=kx+4,得k=-2.
∵二次函数图象的顶点(0,c)为两函数图象的另一个交点,
∴c=4.
把(1,2)代入y=ax2+c,得a+c=2,解得a=-2.
∴k=-2,a=-2,c=4.
(2)由(1)得二次函数表达式为y=-2x2+4,
令y=m,得2x2+m-4=0,解得x1=2?????2,x2=-2?????2,
∴BC=22?????2,
∵OA=m,
∴W=OA2+BC2=m2-2m+8=(m-1)2+7.
∴当m=1时,W取得最小值,最小值为7.
?
14.原创题某电器公司推出一款智能空调扇.经市场调研发现,该产品的月销售量y(台)与销售单价x(元)之间满足如图所示的一次函数关系,已知该产品的成本是每台1 500元.
(1)求出y关于x的函数表达式.
(2)设月销售利润为w(元),求w关于x的函数表达式,并求出当销售单价定为多少时,月销售利润最大,最大月销售利润是多少.
(3)公司开展了技术创新,以降低成本.预计在今后的销售中,月销售量与销售单价仍存在(1)中的函数关系.若想实现当销售单价为1 900元时,月销售利润不低于114 000元的销售目标,则该产品的成本单价应不超过多少元?
答案
14.【解析】 (1)设y关于x的函数表达式为y=kx+b,
将(1 800,200),(2 000,180)分别代入,
得1?800????+????=200,2?000????+????=180,解得????=?110,????=380,
故y关于x的函数表达式为y=-110x+380.
(2)根据题意可知,w关于x的函数表达式为w=(x-1 500)y=(x-1 500)×(-110x+380)=-110x2+530x-570 000,
配方,得w=-110(x-2 650)2+132 250,
所以当x=2 650时,w取得最大值,最大值为132 250,
故当销售单价定为2 650元时,月销售利润最大,最大月销售利润为132 250元.
?
答案
(3)设技术创新后该产品的成本为每台z元,
根据题意可得(1 900-z)(-110×1 900+380)≥114 000,
解得z≤1 300,
故该产品的成本单价应不超过1 300元.
?
15.[2020甘肃二诊]如图,已知二次函数y=x2+bx+c的图象与x轴交于点A(1,0),B(3,0),与y轴交于点C.
(1)求二次函数的表达式;
(2)若点P为抛物线上的一点,点F为其对称轴上的一点,且以点A,B,P,F为顶点的四边形为平行四边形,求点P的坐标;
(3)点E是二次函数第四象限图象上一点,过点E作x轴的垂线,交直线BC于点D,求四边形AEBD面积的最大值及此时点E的坐标.
答案
15.【解析】 (1)因为二次函数y=x2+bx+c的图象与x轴交于点A(1,0),B(3,0),所以y=(x-1)(x-3)=x2-4x+3,
故二次函数的表达式为y=x2-4x+3.
(2)抛物线y=x2-4x+3的对称轴为x=2,AB=2.
①当AB为平行四边形的一条边时,则PF=AB=2,当点P在对称轴右侧时,如图1,?
设点P的坐标为(4,m),
将P(4,m)代入y=x2-4x+3,得m=3,
所以点P的坐标为(4,3).
当点P在对称轴左侧时,即点C的位置,
当x=0时,y=3,
所以P(0,3),
故点P的坐标为(4,3)或(0,3).
答案
②当AB是平行四边形的对角线时,如图2,
AB中点的坐标为(2,0),点F的横坐标为2,
易知AF=FB,所以平行四边形APBF为菱形,
此时点P与抛物线的顶点重合,
所以点P的坐标为(2,-1).
综上所述,点P的坐标为(4,3),(0,3)或(2,-1).
(3)如图3,易知直线BC的表达式为y=-x+3.
设点E的坐标为(x,x2-4x+3),则点D的坐标为(x,-x+3),
所以S四边形AEBD=12AB(yD-yE)=-x+3-x2+4x-3=-x2+3x=-(x-32)2+94.
所以当x=32时,取得最大值,最大值为94,此时点E的坐标为(32,-34).
?
16.[2019河南中考]如图,抛物线y=ax2+12x+c交x轴于A,B两点,交y轴于点C.直线y=-12x-2经过点A,C.
(1)求抛物线的表达式;
(2)点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.
①当△PCM是直角三角形时,求点P的坐标;
②作点B关于点C的对称点B',则平面内存在直线l,使点M,B,B'到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线l:y=kx+b的表达式.(k,b可用含m的式子表示)
?
答案
16.【解析】 (1)当x=0时,y=-12x-2=-2,
∴点C的坐标为(0,-2).
当y=0时,y=-12x-2=0,
解得x=-4,∴点A的坐标为(-4,0).
将A(-4,0),C(0,-2)代入y=ax2+12x+c,
得16?????2+????=0,????=?2,解得????=14,????=?2,
∴抛物线的表达式为y=14x2+12x-2.
(2)①∵PM⊥x轴,∴∠PMC≠90°,∴分两种情况考虑.
(i)当∠MPC=90°时,PC∥x轴,
∴点P的纵坐标为-2.
?
答案
当y=-2时,14x2+12x-2=-2,
解得x1=-2,x2=0,
∴点P的坐标为(-2,-2).
(ii)当∠PCM=90°时,如图所示,设PC与x轴交于点D.
∵∠OAC+∠OCA=90°,∠OCA+∠OCD=90°,
∴∠OAC=∠OCD,
又∵∠AOC=∠COD=90°,
∴△AOC∽△COD,
∴????????????????=????????????????,即24=????????2,
∴OD=1,
∴点D的坐标为(1,0).
设直线PC的表达式为y=kx+b(k≠0),
?
答案
将C(0,-2),D(1,0)代入y=kx+b,得
????=?2,????+????=0,解得????=2,????=?2,
∴直线PC的表达式为y=2x-2.
∴2x-2=14x2+12x-2,
解得x1=0(舍去),x2=6,
当x=6时,y=2x-2=10,
∴点P的坐标为(6,10).
综上所述,当△PCM是直角三角形时,点P的坐标为(-2,-2)或(6,10).
②直线l的表达式为y=-????+42?????4x-2或y=?????+42????+4x-2或y=x-34m-2.
当y=0时,抛物线y=14x2+12x-2=0,
解得x1=-4,x2=2,
∴点B的坐标为(2,0).
?
答案
∵点C的坐标为(0,-2),点B,B'关于点C对称,∴点B'的坐标为(-2,-4).
∵点P的横坐标为m(m>0),
∴点M的坐标为(m,-12m-2),
∴直线BM的表达式为y=-????+42?????4x+????+4?????2,
直线B'M的表达式为y=?????+42????+4x-5????+4????+2,
直线BB'的表达式为y=x-2.
分情况讨论:
当直线l∥BM且过点C时,直线l的表达式为y=-????+42?????4x-2;
当直线l∥B'M且过点C时,直线l的表达式为y=?????+42????+4x-2;
当直线l∥BB'且过线段CM的中点N(12m,-14m-2)时,直线l的表达式为y=x-34m-2.
综上所述,直线l的表达式为y=-????+42?????4x-2或y=?????+42????+4x-2或y=x-34m-2.
?
第二章 二次函数
数学·九年级下册·北师
答案
1.B 【解析】 A项,由二次函数的图象,知a>0,b>0,由一次函数的图象,知a<0,b>0,故A不正确;B项,由二次函数的图象,知a<0,b<0,由一次函数的图象,知a<0,b<0,故B正确;C项,由二次函数的图象,知a>0,b<0,由一次函数的图象,知a>0,
b>0,故C不正确;D项,由二次函数的图象,知a<0,b>0,由一次函数的图象,知a>0,b<0,故D不正确.故选B.
1.[2019甘肃庆阳期中]在同一平面直角坐标系中,二次函数y=ax2+b与一次函数y=ax+2b(ab≠0)的图象可能是 ( )
答案
2.B 【解析】 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,所以x=-????2????=-1,所以b=2a,因为抛物线开口向上,所以a>0,所以b>a,故①错误;由题图知,c<0,当x=-2时,y=ax2+bx+c=4a-2b+c=c<0,故②正确;抛物线与x轴有两个交点,故b2-4ac>0,故③错误;当x=1时,y=a+b+c>0,因为b=2a,所以3b+2c>0,故④正确;当x=-1时,y取得最小值,即am2+bm+c≥a-b+c,故m(am+b)+b≥a(m是任意实数),故⑤错误.故选B.
?
2.[2020湖北黄石模拟]抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,其图象如图所示.给出下列结论:①a>b>c;②4a-2b+c<0;③b2-4ac<0;④3b+2c>0;⑤m(am+b)+b>a(m是任意实数).其中正确的个数是 ( )
A.3 B.2 C.1 D.0
答案
3.C 【解析】 由题意知,抛物线开口向下,对称轴为直线x=m,当-2≤x≤1时,①若m<-2,则当x=-2时,二次函数有最大值,此时-(-2-m)2+m2+1=4,解得m=-74,与m<-2矛盾,故舍去;②若-2≤m≤1,则当x=m时,二次函数有最大值,此时m2+1=4,解得m1=-3,m2=3(舍去);③若m>1,则当x=1时,二次函数有最大值,此时-(1-m)2+m2+1=4,解得m=2.综上所述,m的值为2或
-3.故选C.
?
3.[2019天津七中月考]已知二次函数y=-(x-m)2+m2+1,当-2≤x≤1时,y有最大值4,则实数m的值为 ( )
A.-74 B.3或-3
C.2或-3 D.2,-3或-74
?
答案
4.5≤m≤11 【解析】 抛物线y=-(x+1)2向上平移的过程中,与正方形ABCD的边(包括四个顶点)有交点时,先经过A点,最后经过C点.设平移后的抛物线表达式为y=-(x+1)2+m,将A点坐标代入,得-4+m=1,解得m=5.将C点坐标代入,得-9+m=
2,解得m=11.结合图象可知,抛物线y=-(x+1)2向上平移m(m>0)个单位长度与正方形ABCD的边(包括四个顶点)有交点,
m的取值范围是5≤m≤11.
4.[2019吉林长春模拟]如图,已知正方形ABCD中,A(1,1),B(1,2),C(2,2),D(2,1),若抛物线y=-(x+1)2向上平移m(m>0)个单位长度与正方形ABCD的边(包括四个顶点)有交点,则m的取值范围是 .?
答案
5.-4?
5.[2020浙江绍兴期末]抛物线y=ax2+c(a≠0)与直线y=6相交于点A,B(点A在点B的左侧),与y轴交于点C(0,-2),且∠ACB为直角,当y<0时,自变量x的取值范围是 .?
6.[2020湖南娄底期末]如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为点A(-3,0),B(1,0),与y轴交于点C(0,-3),顶点为D,其对称轴与x轴交于点E.
(1)求二次函数的表达式;
(2)点P为第三象限内抛物线上一点,△APC的面积记为S,求S的最大值及此时点P的坐标.
答案
6.【解析】 (1)由二次函数的图象过A(-3,0),B(1,0)两点,
设二次函数的表达式为y=a(x+3)(x-1),
∵二次函数的图象过点C(0,-3),∴-3=a(0+3)(0-1),
解得a=1,
∴y=(x+3)(x-1)=x2+2x-3.
即二次函数的表达式为y=x2+2x-3.
(2)设直线AC的表达式为y=kx+h,
∵点A的坐标为(-3,0),点C的坐标为(0,-3),
∴?3????+h=0,h=?3,解得????=?1,h=?3,
∴直线AC的表达式为y=-x-3.
如图,过点P作x轴的垂线交AC于点G,设点P的坐标为(x,x2+2x-3),
则点G的坐标为(x,-x-3),
?
答案
∵点P在第三象限,
∴PG=-x-3-(x2+2x-3)=-x2-3x,
∴S=12PG·OA=12(-x2-3x)×3=-32(x+32)2+278,
∴当x=-32时,S取得最大值,最大值是278,此时点P的坐标是(-32,-154).
?
7.[2020河北唐山路南区期末]游乐园一种新型水上滑道如图所示,其中线段PA表示距离水面(x轴)高度为5 m的平台(点P在y轴上).滑道AB可以看作反比例函数图象的一部分,滑道BCD可以看作二次函数图象的一部分,两滑道的连接点B为二次函数图象的顶点,且点B到水面的距离BE=2 m,点B到y轴的距离是5 m.当小明从上面下滑到点C时,与水面的距离CG=32 m,与点B的水平距离CF=2 m.
(1)求反比例函数的关系式及其自变量的取值范围;
(2)求整条滑道ABCD的水平宽度;
(3)若小明站在平台上相距y轴1 m的点M处,用水枪朝正前方“扫射”,水枪出口N距离平台32 m,喷出的水流呈抛物线型,点N是抛物线的顶点.设这条抛物线的二次项系数为p,若水流最终落在滑道BCD上(包括B,D两点),直接写出p的取值范围.
?
答案
7.【解析】 (1)由题意,得点B(5,2),
设反比例函数的表达式为y=????????,则k=5×2=10,
所以反比例函数的表达式为y=10????.
当y=5时,x=2,即点A(2,5),
所以反比例函数自变量的取值范围为2≤x≤5.
(2)由题意,知点B(5,2),点C(7,32),设二次函数的表达式为y=a(x-5)2+2,
将点C的坐标代入,得32=a(7-5)2+2,解得a=-18.
故二次函数的表达式为y=-18(x-5)2+2.
令y=0,得x=1(舍去)或x=9,
故滑道ABCD的水平宽度为9-2=7(m).
?
答案
(3)-932≤p≤-13128.
由题意知,点N(1,132),且点N是抛物线的顶点,
由(2)知,点D(9,0).
设抛物线的表达式为y=p(x-1)2+132,
将点D的坐标代入上式,得0=p(9-1)2+132,解得p=-13128.
同理,把点B的坐标代入上式,解得p=-932,
故-932≤p≤-13128.
?
答案
1.B 【解析】 由题意,知抛物线的对称轴为直线x=-?122×(?3)=-2,∵a=-3<0,∴当x=-2时,函数值最大,又∵-3到-2的距离比1到-2的距离小,∴y3?
1.[2020浙江温州中考]已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则 ( )
A.y3C.y2答案
2.D 【解析】 因为二次函数y=ax2+bx+c的图象开口向上,所以a>0.因为抛物线的对称轴为直线x=-????2????>0,所以b<0.因为抛物线与y轴的交点在y轴的正半轴,所以c>0,所以一次函数y=ax+b的图象经过第一、三、四象限,反比例函数y=????????的图象经过第一、三象限.故选D.
?
2.[2020新疆中考]二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y=????????在同一平面直角坐标系中的图象可能是 ( )
?
答案
3.C 【解析】 y=x(4-x)=-x2+4x=-(x-2)2+4,∴抛物线开口向下,顶点坐标是(2,4),函数的最大值是4.∵点P(a,b)在抛物线上,∴当b=5时,点P的个数为0;当b=4时,点P的个数为1;当b=3时,点P的个数为2.故甲、乙的说法正确,丙的说法错误.故选C.
3.[2020河北中考]如图,现要在抛物线y=x(4-x)上找点P (a,b),针对b的不同取值,?所找点P的个数,三人的说法如下.
甲:若b=5,则点P的个数为0.
乙:若b=4,则点P的个数为1.
丙:若b=3,则点P的个数为1.
下列判断正确的是 ( )
A.乙错,丙对 B.甲和乙都错
C.乙对,丙错 D.甲错,丙对
答案
4.C 【解析】 ∵抛物线的对称轴为直线x=-????2????=-2,∴4a-b=0,故①正确;∵抛物线与x轴的一个交点在(-3,0)和(-4,0)之间,∴由抛物线的对称性知,另一个交点在(-1,0)和(0,0)之间,∴x=-1时,y>0,且b=4a,∴a-b+c=a-4a+c=-3a+c>0,即c>3a,故②错误;∵抛物线开口向下,且顶点坐标为(-2,3),∴抛物线与直线y=2有两个交点,∴关于x的方程ax2+bx+c=2有两个不相等实数根,故③正确;∵抛物线的顶点坐标为(-2,3),∴4?????????????24????=3,∴b2+12a=4ac,∵b=4a,∴b2+3b=4ac,∵a<0,
∴b=4a<0,∴b2+2b>4ac,故④正确.综上,①③④正确.故选C.
?
4.[2020贵州遵义中考]抛物线y=ax2+bx+c的对称轴是直线x=-2.抛物线与x轴的一个交点在点(-4,0)和点(-3,0)之间,其部分图象如图所示,下列结论中正确的个数有 ( )
①4a-b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等实数根;④b2+2b>4ac.
A.1 B.2 C.3 D.4
5.[2020贵州黔西南州中考]如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x=52,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是 ( )
A.点B坐标为(5,4) B.AB=AD
C.a=-16 D.OC·OD=16
?
答案
5.D 【解析】 ∵抛物线y=ax2+bx+4交y轴于点A,∴点A的坐标为(0,4),∵对称轴为直线x=52,AB∥x轴,∴点B的坐标为(5,4),故A项结论正确.如图,过点B作BE⊥x轴于点E,则BE=4,AB=5,∵AB∥x轴,∴∠BAC=∠ACO,∵点B关于直线AC的对称点恰好落在线段OC上,∴∠ACO=∠ACB,∴∠BAC=∠ACB,∴BC=AB=5,在Rt△BCE中,由勾股定理得EC=3,∴点C的坐标为(8,0).∵对称轴为直线x=52,∴点D的坐标为(-3,0).在Rt△ADO中,OA=4,OD=3,∴AD=5, ∴AB=AD,故B项结论正确.设y=ax2+bx+4=a(x+3)(x-8),将A(0,4)代入,得4=a(0+3)(0-8),∴a=-16,故C项结论正确.∵OC=8,OD=3,∴OC·OD=24,故D项结论错误.故选D.
?
6.[2020浙江台州中考]用各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆体水桶水面离地面的高度为H(单位:cm),如果在离水面竖直距离为h(单位:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系为s2=4h(H-h).
应用思考:现用高度为20 cm的圆柱体塑料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距离h cm处开一个小孔.
(1)写出s2与h的关系式;并求出当h为何值时,射程s有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,求a,b之间的关系式.
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加16 cm,求垫高的高度及小孔离水面的竖直距离.
答案
6.【解析】 (1)s2=4h(H-h),
当H=20时,s2=4h(20-h)=-4(h-10)2+400,
当h=10时,s2有最大值400,此时,s有最大值20.
∴当h为10时,射程s有最大值,最大射程是20 cm.
(2)由(1)知,s2=4h(20-h),设存在a,b,使两孔射出水的射程相同,则4a(20-a)=4b(20-b),
∴20a-a2=20b-b2,a2-b2=20a-20b,
(a+b)(a-b)=20(a-b),
(a-b)(a+b-20)=0,
∴a-b=0,或a+b-20=0,
∴a=b或a+b=20.
答案
(3)设垫高的高度为m,则s2=4h(20+m-h)=-4(h-20+????2)2+(20+m)2,
∴当h=20+????2时,s最大=20+m=20+16,
∴m=16,此时h=20+????2=18,
∴垫高的高度为16 cm,小孔离水面的竖直距离为18 cm.
?
7.[2020陕西中考]如图,抛物线y=x2 +bx+c经过点(3,12)和(-2, -3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.
(1)求该抛物线的表达式;
(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P,D,E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.
答案
7.【解析】 (1)由题意,得
12=9+3????+????,?3=4?2????+????,解得????=2,????=?3,
∴y=x2 +2x-3.
(2)由(1)可得,对称轴l:x=-1.
令y=0,则x2 +2x-3=0,
解得x1=-3,x2=1.
∴A(-3,0),B(1,0).
令x=0,则y=-3,∴C(0,-3),∴OA=OC=3.
∵∠PDE=∠AOC=90°,
∴当PD=DE=3时,△PDE与△AOC全等.
?
答案
设P(m,n),当点P在l右侧时,m-(-1)=3.
∴m=2,∴n=22+2×2-3=5,∴P(2,5).
∴E(-1,2)或E(-1,8).
当点P在l左侧时,由抛物线的对称性可知,P(-4,5)也满足条件.
相应的点E的坐标同上,
∴满足条件的点P的坐标为(2,5)或(-4.5),点E的坐标为(-1,2)或(-1,8).
数学·九年级下册·北师
函数是反映现实世界中数量关系和变化规律的一种常见数学模型,函数的图象是研究函数性质的重要工具,体现数形结合思想的应用.解决与二次函数图象、性质有关的问题,关键是明确表达式的系数与图象的关系,能将数、形有机结合,相互转化;应用二次函数解决实际问题时,要特别注意自变量取值范围的限制条件.例如,第2题,根据绝对值的几何意义画出函数y=|ax2+bx+c|的图象,结合图象判断方程有两个不相等的实数根的条件,培养学生的分类讨论思想和分析问题、解决问题的能力;第3题,利用根的判别式探究直线与双抛物线的交点问题,关注直观想象.
1.[动态几何引发的函数图象问题][2019辽宁锦州中考]如图,在菱形ABCD中,∠B=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD运动到点D,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是 ( )
答案
1.B 【解析】 当P,Q分别在AB,AC上运动时,∵四边形ABCD是菱形,∠B=60°,∴△ABC,△ACD都是边长为2的等边三角形,如图,过点Q作QH⊥AB于点H,y=12AP×QH=12(2-x)×xsin 60°=-34x2+32x=-34(x-1)2+34;当P,Q分别在AC,DC上运动时,同理可得y=34(x-2)2.故选B.
?
2.[二次函数与绝对值方程]二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是 ( )
A.k<-3 B.k>-3
C.k<3 D.k>3
答案
2.D 【解析】 当ax2+bx+c≥0时,y=|ax2+bx+c|=ax2+bx+c,此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c(a≠0)在x轴上方部分的图象(包括与x轴的交点);当ax2+bx+c<0时,y=
|ax2+bx+c|=-(ax2+bx+c),此时y=|ax2+bx+c|的图象是函数 y=ax2+bx+c(a≠0)在x轴下方部分与x轴对称的图象.所以y=|ax2+bx+c|的图象如图所示.观察图象可得,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k>3.故选D.
3.[直线与双抛物线的交点问题][2019天津七中月考]如图,抛物线y=-2x2+8x-6与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是 .?
答案
3.-3
4.[筛选有效数据解决二次函数问题][2019山东威海中考]在画二次函数y=ax2+bx+c(a≠0)的图象时,甲写错了一次项的系数,列表如下:
乙写错了常数项,列表如下:
通过上述信息,解决以下问题:
(1)求原二次函数y=ax2+bx+c(a≠0)的表达式;
(2)对于二次函数y=ax2+bx+c(a≠0),当x 时,y的值随x的值增大而增大;?
(3)若关于x的方程ax2+bx+c=k(a≠0)有两个不相等的实数根,求k的取值范围.
x
?
-1
0
1
2
3
?
y甲
?
6
3
2
3
6
?
x
?
-1
0
1
2
3
?
y乙
?
-2
-1
2
7
14
?
答案
4.【解析】 (1)由甲同学的列表知c=3,由此可将乙同学的列表修正为:
把x=-1,y=2;x=1,y=6代入y=ax2+bx+3,得
?????????+3=2,????+????+3=6,解得????=1,????=2,
∴原二次函数的表达式为y=x2+2x+3.
(2)≥-1
二次函数y=x2+2x+3图象的对称轴为直线x=-22×1=-1,∵抛物线的开口向上,∴当x≥-1时,y的值随x的值增大而增大.
?
x
?
-1
0
1
2
3
?
y乙
?
2
3
6
11
18
?
答案
(3)解法一 关于x的方程ax2+bx+c=k(a≠0)有两个不相等的实数根,
即x2+2x+3-k=0有两个不相等的实数根,
∴Δ=4-4(3-k)>0,解得k>2.
解法二 由关于x的方程ax2+bx+c=k(a≠0)有两个不相等的实数根,得直线y=k与抛物线y=x2+2x+3有两个交点.
∵抛物线y=x2+2x+3的顶点坐标为(-1,2),且开口向上,
∴k的取值范围为k>2.
答案
1.B 【解析】 y=-x2+4x+3=-(x-2)2+7,所以该抛物线的顶点坐标是(2,7).故选B.
一、选择题
1.[2020福建莆田秀屿区期中]抛物线y=-x2+4x+3的顶点坐标为 ( )
A.(-2,7) B.(2,7)
C.(2,-9) D.(-2,-9)
答案
2.B 【解析】 ∵抛物线y=-x2+bx+4经过(-2,n)和(4,n)两点,∴抛物线的对称轴为直线x=1,∴????2=1,解得b=2,∴y=-x2+
2x+4.将(-2,n)代入y=-x2+2x+4,得n=-4.故选B.
?
2.[2019河南中考]已知抛物线y=-x2+bx+4经过(-2,n)和(4,n)两点,则n的值为 ( )
A.-2 B.-4 C.2 D.4
答案
3.C 【解析】 A项,由二次函数图象开口向上,对称轴在y轴右侧,得a>0,b<0,由一次函数图象可知b>0,两者矛盾,故A项不合题意;B项,由方程组????=????????2+????????,????=?????????????,得ax2=-a,因为a≠0,所以x2=-1,所以该方程组无实数根,故二次函数图象与一次函数图象无交点,故B项不合题意;C项,由二次函数开口向上,对称轴在y轴右侧,得a>0,b<0,由一次函数图象得b<0,a>0,所以C项符合题意;D项,二次函数的图象应过原点,故D项不合题意.故选C.
?
3.[2019四川攀枝花中考]在同一坐标系中,二次函数y=ax2+bx与一次函数y=bx-a的图象可能是 ( )
答案
4.C 【解析】 抛物线y=x2+(m+1)x+m的开口向上,对称轴为直线x=-????+12.因为当x=1时,y>0,所以12+m+1+m>0,解得m>-1.因为当x<-2时, y随x的增大而减小,所以-????+12≥-2,解得m≤3.故m的取值范围为-1
4.已知抛物线y=x2+(m+1)x+m,当x=1时,y>0,且当x<-2时, y随x的增大而减小,则m的取值范围是 ( )
A.m>-1 B.m<3
C.-1
5.D 【解析】 一元二次方程ax2+bx+c+7=0的根是抛物线y=ax2+bx+c与直线y=-7的交点的横坐标.由题中表格,可知抛物线y=ax2+bx+c与直线y=-7的一个交点为(3,-7).因为当x=-2和x=0时,函数值都是4,所以抛物线y=ax2+bx+c的对称轴是直线x=-1.根据抛物线的对称性,可知抛物线y=ax2+bx+c与直线y=-7的另一个交点坐标为(-5,-7),所以一元二次方程ax2+bx+c+7=0的根是x1=-5,x2=3.故选D.
5.已知二次函数y=ax2+bx+c(a≠0),下表列出了该函数x,y的部分对应值,则一元二次方程ax2+bx+c+7=0的根是 ( )
A.x1=2,x2=-3 B.x1=-5,x2=-3
C.x1=-4,x2=3 D.x1=-5,x2=3
x
?
-2
-1
0
1
2
3
?
y
?
4
5
4
2
-1
-7
?
答案
6.B 【解析】 因为抛物线的顶点A的坐标为(-3,0),所以可设B(-3-m,2)(m>0),则C(-3+m,2),所以BC=2m.因为△ABC为等边三角形,所以AC=2m,所以m2+22=(2m)2,所以m=233,所以C(-3+233,2).设抛物线的表达式为y=a(x+3)2,将点C的坐标代入,得a(-3+233+3)2=2,解得a=32,所以y=32(x+3)2,当x=0时,y=272,所以此抛物线与y轴的交点坐标为(0,272).故选B.
?
6.如图,平面直角坐标系内有一顶点为A的抛物线,此抛物线与直线y=2交于B,C两点,△ABC为等边三角形.若点A的坐标为(-3,0),则此抛物线与y轴的交点坐标为 ( )
A.(0,92) B.(0,272) C.(0,9) D.(0,19)
?
答案
7.A 【解析】 如图,以A为坐标原点,AE所在直线为x轴,AB所在直线为y轴,建立平面直角坐标系.根据题意知,抛物线的顶点C的坐标为(1.6,2.5),设抛物线的表达式为y=a(x-1.6)2+2.5,将点B(0,1.5)代入,得2.56a+2.5=1.5,解得a=-12.56,所以抛物线的表达式为y=-12.56(x-1.6)2+2.5.当y=1.86时,-12.56(x-1.6)2+2.5=1.86,解得x1=0.32(舍去),x2=2.88.所以茶几到灯柱的距离AE为2.88 m.故选A.
?
7.[2020河北衡水模拟]如图是一款抛物线型落地灯筒示意图,灯柱AB的高为1.5 m,防滑螺母C为抛物线支架的最高点,距灯柱的水平距离为1.6 m,灯罩D距离地面1.86 m,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为 ( )?
A.2.88 m B.3.2 m C.2.5 m D.1.6 m
8.[2019四川达州中考]如图,边长都为4的正方形ABCD和正三角形EFG如图放置,AB与EF在一条直线上,点A与点F重合.现将△EFG沿AB方向以每秒1个单位长度的速度匀速运动,当点F与B重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是 ( )
答案
8.C 【解析】 当0≤t≤2时,如图1,设GF与AD交于点M,AF=t,AM=AF·tan 60°=3t,所以S=12AF·AM=32t2,即S与t是二次函数关系,其图象开口向上,有最小值0.当2
答案
9.3 【解析】 设平移后的抛物线为y=(x-3+a)2-2(a>0),因为该抛物线经过点A(2,2),所以2=(2-3+a)2-2,解得a=3或a=
-1(舍去),故将抛物线y=(x-3)2-2向左平移3个单位长度后经过点A(2,2).
二、填空题
9.[2019四川凉山州中考]将抛物线y=(x-3)2-2向左平移 个单位长度后经过点A(2,2).?
答案
10.-2 【解析】 设OA,BC交于点D.∵四边形ABOC是正方形,∴BC⊥OA,OD=BD,∴点B的坐标为(-????2????,-????2????).∵抛物线y=ax2过点B,∴-????2????=a(-????2????)2,解得b1=0(舍去),b2=-2.
?
10.如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx(a>0)的顶点为C,与x轴的正半轴交于点A,它的对称轴与抛物线y=ax2(a>0)交于点B.若四边形ABOC是正方形,则b的值是 .?
答案
11.2 【解析】 ∵y=ax2-2ax+83=a(x-1)2-a+83(a>0),且抛物线与y轴交于点A,∴A的坐标为(0,83),抛物线的对称轴为x=1,顶点P的坐标为(1,83-a),∴点M的坐标为(2,83).∵点M为线段AB的中点,∴点B的坐标为(4,83).设直线OP的函数表达式为y=kx(k为常数,且k≠0),将点B(4,83)代入,得83=4k,解得k=23,即直线OP的函数表达式为y=23x.将点P(1, 83-a)代入y=23x,得83-a=23,解得a=2.
?
11.[2019吉林长春中考]如图,在平面直角坐标系中,抛物线y=ax2-2ax+83(a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M,P为抛物线的顶点.若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为 .?
?
答案
12.3 【解析】 ∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=-????2????=1,∴b=-2a>0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc<0,故①正确;由图象的对称性知,当x=2时,y>0,即4a+2b+c>0,∴a+12b+14c>0,故②正确;∵点C的坐标为(0,c),OA=OC,∴点A的坐标为(-c,0),把A(-c,0)代入y=ax2+bx+c,得ac2-bc+c=0,∴ac-b+1=0,故③错误;∵点A的坐标为
(-c,0),对称轴为直线x=1,∴点B的坐标为(2+c,0),∴2+c是关于x的一元二次方程ax2+bx+c=0的一个根,故④正确.综上所述,①②④正确,有3个.
?
12.[2020湖北随州模拟]如图,已知二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,OA=OC,对称轴为直线x=1,给出下列结论:①abc<0;②a+12b+14c>0;③ac+b+1=0;④2+c是关于x的一元二次方程ax2+bx+c=0的一个根.其中正确的结论有 个.?
?
三、解答题
13.[2019安徽中考]一次函数y=kx+4与二次函数y=ax2+c的图象的一个交点的坐标为(1,2),另一个交点是该二次函数图象的顶点.
(1)求k,a,c的值;
(2)过点A(0,m)(0
13.【解析】 (1)把(1,2)代入y=kx+4,得k=-2.
∵二次函数图象的顶点(0,c)为两函数图象的另一个交点,
∴c=4.
把(1,2)代入y=ax2+c,得a+c=2,解得a=-2.
∴k=-2,a=-2,c=4.
(2)由(1)得二次函数表达式为y=-2x2+4,
令y=m,得2x2+m-4=0,解得x1=2?????2,x2=-2?????2,
∴BC=22?????2,
∵OA=m,
∴W=OA2+BC2=m2-2m+8=(m-1)2+7.
∴当m=1时,W取得最小值,最小值为7.
?
14.原创题某电器公司推出一款智能空调扇.经市场调研发现,该产品的月销售量y(台)与销售单价x(元)之间满足如图所示的一次函数关系,已知该产品的成本是每台1 500元.
(1)求出y关于x的函数表达式.
(2)设月销售利润为w(元),求w关于x的函数表达式,并求出当销售单价定为多少时,月销售利润最大,最大月销售利润是多少.
(3)公司开展了技术创新,以降低成本.预计在今后的销售中,月销售量与销售单价仍存在(1)中的函数关系.若想实现当销售单价为1 900元时,月销售利润不低于114 000元的销售目标,则该产品的成本单价应不超过多少元?
答案
14.【解析】 (1)设y关于x的函数表达式为y=kx+b,
将(1 800,200),(2 000,180)分别代入,
得1?800????+????=200,2?000????+????=180,解得????=?110,????=380,
故y关于x的函数表达式为y=-110x+380.
(2)根据题意可知,w关于x的函数表达式为w=(x-1 500)y=(x-1 500)×(-110x+380)=-110x2+530x-570 000,
配方,得w=-110(x-2 650)2+132 250,
所以当x=2 650时,w取得最大值,最大值为132 250,
故当销售单价定为2 650元时,月销售利润最大,最大月销售利润为132 250元.
?
答案
(3)设技术创新后该产品的成本为每台z元,
根据题意可得(1 900-z)(-110×1 900+380)≥114 000,
解得z≤1 300,
故该产品的成本单价应不超过1 300元.
?
15.[2020甘肃二诊]如图,已知二次函数y=x2+bx+c的图象与x轴交于点A(1,0),B(3,0),与y轴交于点C.
(1)求二次函数的表达式;
(2)若点P为抛物线上的一点,点F为其对称轴上的一点,且以点A,B,P,F为顶点的四边形为平行四边形,求点P的坐标;
(3)点E是二次函数第四象限图象上一点,过点E作x轴的垂线,交直线BC于点D,求四边形AEBD面积的最大值及此时点E的坐标.
答案
15.【解析】 (1)因为二次函数y=x2+bx+c的图象与x轴交于点A(1,0),B(3,0),所以y=(x-1)(x-3)=x2-4x+3,
故二次函数的表达式为y=x2-4x+3.
(2)抛物线y=x2-4x+3的对称轴为x=2,AB=2.
①当AB为平行四边形的一条边时,则PF=AB=2,当点P在对称轴右侧时,如图1,?
设点P的坐标为(4,m),
将P(4,m)代入y=x2-4x+3,得m=3,
所以点P的坐标为(4,3).
当点P在对称轴左侧时,即点C的位置,
当x=0时,y=3,
所以P(0,3),
故点P的坐标为(4,3)或(0,3).
答案
②当AB是平行四边形的对角线时,如图2,
AB中点的坐标为(2,0),点F的横坐标为2,
易知AF=FB,所以平行四边形APBF为菱形,
此时点P与抛物线的顶点重合,
所以点P的坐标为(2,-1).
综上所述,点P的坐标为(4,3),(0,3)或(2,-1).
(3)如图3,易知直线BC的表达式为y=-x+3.
设点E的坐标为(x,x2-4x+3),则点D的坐标为(x,-x+3),
所以S四边形AEBD=12AB(yD-yE)=-x+3-x2+4x-3=-x2+3x=-(x-32)2+94.
所以当x=32时,取得最大值,最大值为94,此时点E的坐标为(32,-34).
?
16.[2019河南中考]如图,抛物线y=ax2+12x+c交x轴于A,B两点,交y轴于点C.直线y=-12x-2经过点A,C.
(1)求抛物线的表达式;
(2)点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.
①当△PCM是直角三角形时,求点P的坐标;
②作点B关于点C的对称点B',则平面内存在直线l,使点M,B,B'到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线l:y=kx+b的表达式.(k,b可用含m的式子表示)
?
答案
16.【解析】 (1)当x=0时,y=-12x-2=-2,
∴点C的坐标为(0,-2).
当y=0时,y=-12x-2=0,
解得x=-4,∴点A的坐标为(-4,0).
将A(-4,0),C(0,-2)代入y=ax2+12x+c,
得16?????2+????=0,????=?2,解得????=14,????=?2,
∴抛物线的表达式为y=14x2+12x-2.
(2)①∵PM⊥x轴,∴∠PMC≠90°,∴分两种情况考虑.
(i)当∠MPC=90°时,PC∥x轴,
∴点P的纵坐标为-2.
?
答案
当y=-2时,14x2+12x-2=-2,
解得x1=-2,x2=0,
∴点P的坐标为(-2,-2).
(ii)当∠PCM=90°时,如图所示,设PC与x轴交于点D.
∵∠OAC+∠OCA=90°,∠OCA+∠OCD=90°,
∴∠OAC=∠OCD,
又∵∠AOC=∠COD=90°,
∴△AOC∽△COD,
∴????????????????=????????????????,即24=????????2,
∴OD=1,
∴点D的坐标为(1,0).
设直线PC的表达式为y=kx+b(k≠0),
?
答案
将C(0,-2),D(1,0)代入y=kx+b,得
????=?2,????+????=0,解得????=2,????=?2,
∴直线PC的表达式为y=2x-2.
∴2x-2=14x2+12x-2,
解得x1=0(舍去),x2=6,
当x=6时,y=2x-2=10,
∴点P的坐标为(6,10).
综上所述,当△PCM是直角三角形时,点P的坐标为(-2,-2)或(6,10).
②直线l的表达式为y=-????+42?????4x-2或y=?????+42????+4x-2或y=x-34m-2.
当y=0时,抛物线y=14x2+12x-2=0,
解得x1=-4,x2=2,
∴点B的坐标为(2,0).
?
答案
∵点C的坐标为(0,-2),点B,B'关于点C对称,∴点B'的坐标为(-2,-4).
∵点P的横坐标为m(m>0),
∴点M的坐标为(m,-12m-2),
∴直线BM的表达式为y=-????+42?????4x+????+4?????2,
直线B'M的表达式为y=?????+42????+4x-5????+4????+2,
直线BB'的表达式为y=x-2.
分情况讨论:
当直线l∥BM且过点C时,直线l的表达式为y=-????+42?????4x-2;
当直线l∥B'M且过点C时,直线l的表达式为y=?????+42????+4x-2;
当直线l∥BB'且过线段CM的中点N(12m,-14m-2)时,直线l的表达式为y=x-34m-2.
综上所述,直线l的表达式为y=-????+42?????4x-2或y=?????+42????+4x-2或y=x-34m-2.
?
第二章 二次函数
数学·九年级下册·北师
答案
1.B 【解析】 A项,由二次函数的图象,知a>0,b>0,由一次函数的图象,知a<0,b>0,故A不正确;B项,由二次函数的图象,知a<0,b<0,由一次函数的图象,知a<0,b<0,故B正确;C项,由二次函数的图象,知a>0,b<0,由一次函数的图象,知a>0,
b>0,故C不正确;D项,由二次函数的图象,知a<0,b>0,由一次函数的图象,知a>0,b<0,故D不正确.故选B.
1.[2019甘肃庆阳期中]在同一平面直角坐标系中,二次函数y=ax2+b与一次函数y=ax+2b(ab≠0)的图象可能是 ( )
答案
2.B 【解析】 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,所以x=-????2????=-1,所以b=2a,因为抛物线开口向上,所以a>0,所以b>a,故①错误;由题图知,c<0,当x=-2时,y=ax2+bx+c=4a-2b+c=c<0,故②正确;抛物线与x轴有两个交点,故b2-4ac>0,故③错误;当x=1时,y=a+b+c>0,因为b=2a,所以3b+2c>0,故④正确;当x=-1时,y取得最小值,即am2+bm+c≥a-b+c,故m(am+b)+b≥a(m是任意实数),故⑤错误.故选B.
?
2.[2020湖北黄石模拟]抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,其图象如图所示.给出下列结论:①a>b>c;②4a-2b+c<0;③b2-4ac<0;④3b+2c>0;⑤m(am+b)+b>a(m是任意实数).其中正确的个数是 ( )
A.3 B.2 C.1 D.0
答案
3.C 【解析】 由题意知,抛物线开口向下,对称轴为直线x=m,当-2≤x≤1时,①若m<-2,则当x=-2时,二次函数有最大值,此时-(-2-m)2+m2+1=4,解得m=-74,与m<-2矛盾,故舍去;②若-2≤m≤1,则当x=m时,二次函数有最大值,此时m2+1=4,解得m1=-3,m2=3(舍去);③若m>1,则当x=1时,二次函数有最大值,此时-(1-m)2+m2+1=4,解得m=2.综上所述,m的值为2或
-3.故选C.
?
3.[2019天津七中月考]已知二次函数y=-(x-m)2+m2+1,当-2≤x≤1时,y有最大值4,则实数m的值为 ( )
A.-74 B.3或-3
C.2或-3 D.2,-3或-74
?
答案
4.5≤m≤11 【解析】 抛物线y=-(x+1)2向上平移的过程中,与正方形ABCD的边(包括四个顶点)有交点时,先经过A点,最后经过C点.设平移后的抛物线表达式为y=-(x+1)2+m,将A点坐标代入,得-4+m=1,解得m=5.将C点坐标代入,得-9+m=
2,解得m=11.结合图象可知,抛物线y=-(x+1)2向上平移m(m>0)个单位长度与正方形ABCD的边(包括四个顶点)有交点,
m的取值范围是5≤m≤11.
4.[2019吉林长春模拟]如图,已知正方形ABCD中,A(1,1),B(1,2),C(2,2),D(2,1),若抛物线y=-(x+1)2向上平移m(m>0)个单位长度与正方形ABCD的边(包括四个顶点)有交点,则m的取值范围是 .?
答案
5.-4
5.[2020浙江绍兴期末]抛物线y=ax2+c(a≠0)与直线y=6相交于点A,B(点A在点B的左侧),与y轴交于点C(0,-2),且∠ACB为直角,当y<0时,自变量x的取值范围是 .?
6.[2020湖南娄底期末]如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为点A(-3,0),B(1,0),与y轴交于点C(0,-3),顶点为D,其对称轴与x轴交于点E.
(1)求二次函数的表达式;
(2)点P为第三象限内抛物线上一点,△APC的面积记为S,求S的最大值及此时点P的坐标.
答案
6.【解析】 (1)由二次函数的图象过A(-3,0),B(1,0)两点,
设二次函数的表达式为y=a(x+3)(x-1),
∵二次函数的图象过点C(0,-3),∴-3=a(0+3)(0-1),
解得a=1,
∴y=(x+3)(x-1)=x2+2x-3.
即二次函数的表达式为y=x2+2x-3.
(2)设直线AC的表达式为y=kx+h,
∵点A的坐标为(-3,0),点C的坐标为(0,-3),
∴?3????+h=0,h=?3,解得????=?1,h=?3,
∴直线AC的表达式为y=-x-3.
如图,过点P作x轴的垂线交AC于点G,设点P的坐标为(x,x2+2x-3),
则点G的坐标为(x,-x-3),
?
答案
∵点P在第三象限,
∴PG=-x-3-(x2+2x-3)=-x2-3x,
∴S=12PG·OA=12(-x2-3x)×3=-32(x+32)2+278,
∴当x=-32时,S取得最大值,最大值是278,此时点P的坐标是(-32,-154).
?
7.[2020河北唐山路南区期末]游乐园一种新型水上滑道如图所示,其中线段PA表示距离水面(x轴)高度为5 m的平台(点P在y轴上).滑道AB可以看作反比例函数图象的一部分,滑道BCD可以看作二次函数图象的一部分,两滑道的连接点B为二次函数图象的顶点,且点B到水面的距离BE=2 m,点B到y轴的距离是5 m.当小明从上面下滑到点C时,与水面的距离CG=32 m,与点B的水平距离CF=2 m.
(1)求反比例函数的关系式及其自变量的取值范围;
(2)求整条滑道ABCD的水平宽度;
(3)若小明站在平台上相距y轴1 m的点M处,用水枪朝正前方“扫射”,水枪出口N距离平台32 m,喷出的水流呈抛物线型,点N是抛物线的顶点.设这条抛物线的二次项系数为p,若水流最终落在滑道BCD上(包括B,D两点),直接写出p的取值范围.
?
答案
7.【解析】 (1)由题意,得点B(5,2),
设反比例函数的表达式为y=????????,则k=5×2=10,
所以反比例函数的表达式为y=10????.
当y=5时,x=2,即点A(2,5),
所以反比例函数自变量的取值范围为2≤x≤5.
(2)由题意,知点B(5,2),点C(7,32),设二次函数的表达式为y=a(x-5)2+2,
将点C的坐标代入,得32=a(7-5)2+2,解得a=-18.
故二次函数的表达式为y=-18(x-5)2+2.
令y=0,得x=1(舍去)或x=9,
故滑道ABCD的水平宽度为9-2=7(m).
?
答案
(3)-932≤p≤-13128.
由题意知,点N(1,132),且点N是抛物线的顶点,
由(2)知,点D(9,0).
设抛物线的表达式为y=p(x-1)2+132,
将点D的坐标代入上式,得0=p(9-1)2+132,解得p=-13128.
同理,把点B的坐标代入上式,解得p=-932,
故-932≤p≤-13128.
?
答案
1.B 【解析】 由题意,知抛物线的对称轴为直线x=-?122×(?3)=-2,∵a=-3<0,∴当x=-2时,函数值最大,又∵-3到-2的距离比1到-2的距离小,∴y3
1.[2020浙江温州中考]已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则 ( )
A.y3
2.D 【解析】 因为二次函数y=ax2+bx+c的图象开口向上,所以a>0.因为抛物线的对称轴为直线x=-????2????>0,所以b<0.因为抛物线与y轴的交点在y轴的正半轴,所以c>0,所以一次函数y=ax+b的图象经过第一、三、四象限,反比例函数y=????????的图象经过第一、三象限.故选D.
?
2.[2020新疆中考]二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y=????????在同一平面直角坐标系中的图象可能是 ( )
?
答案
3.C 【解析】 y=x(4-x)=-x2+4x=-(x-2)2+4,∴抛物线开口向下,顶点坐标是(2,4),函数的最大值是4.∵点P(a,b)在抛物线上,∴当b=5时,点P的个数为0;当b=4时,点P的个数为1;当b=3时,点P的个数为2.故甲、乙的说法正确,丙的说法错误.故选C.
3.[2020河北中考]如图,现要在抛物线y=x(4-x)上找点P (a,b),针对b的不同取值,?所找点P的个数,三人的说法如下.
甲:若b=5,则点P的个数为0.
乙:若b=4,则点P的个数为1.
丙:若b=3,则点P的个数为1.
下列判断正确的是 ( )
A.乙错,丙对 B.甲和乙都错
C.乙对,丙错 D.甲错,丙对
答案
4.C 【解析】 ∵抛物线的对称轴为直线x=-????2????=-2,∴4a-b=0,故①正确;∵抛物线与x轴的一个交点在(-3,0)和(-4,0)之间,∴由抛物线的对称性知,另一个交点在(-1,0)和(0,0)之间,∴x=-1时,y>0,且b=4a,∴a-b+c=a-4a+c=-3a+c>0,即c>3a,故②错误;∵抛物线开口向下,且顶点坐标为(-2,3),∴抛物线与直线y=2有两个交点,∴关于x的方程ax2+bx+c=2有两个不相等实数根,故③正确;∵抛物线的顶点坐标为(-2,3),∴4?????????????24????=3,∴b2+12a=4ac,∵b=4a,∴b2+3b=4ac,∵a<0,
∴b=4a<0,∴b2+2b>4ac,故④正确.综上,①③④正确.故选C.
?
4.[2020贵州遵义中考]抛物线y=ax2+bx+c的对称轴是直线x=-2.抛物线与x轴的一个交点在点(-4,0)和点(-3,0)之间,其部分图象如图所示,下列结论中正确的个数有 ( )
①4a-b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等实数根;④b2+2b>4ac.
A.1 B.2 C.3 D.4
5.[2020贵州黔西南州中考]如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x=52,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是 ( )
A.点B坐标为(5,4) B.AB=AD
C.a=-16 D.OC·OD=16
?
答案
5.D 【解析】 ∵抛物线y=ax2+bx+4交y轴于点A,∴点A的坐标为(0,4),∵对称轴为直线x=52,AB∥x轴,∴点B的坐标为(5,4),故A项结论正确.如图,过点B作BE⊥x轴于点E,则BE=4,AB=5,∵AB∥x轴,∴∠BAC=∠ACO,∵点B关于直线AC的对称点恰好落在线段OC上,∴∠ACO=∠ACB,∴∠BAC=∠ACB,∴BC=AB=5,在Rt△BCE中,由勾股定理得EC=3,∴点C的坐标为(8,0).∵对称轴为直线x=52,∴点D的坐标为(-3,0).在Rt△ADO中,OA=4,OD=3,∴AD=5, ∴AB=AD,故B项结论正确.设y=ax2+bx+4=a(x+3)(x-8),将A(0,4)代入,得4=a(0+3)(0-8),∴a=-16,故C项结论正确.∵OC=8,OD=3,∴OC·OD=24,故D项结论错误.故选D.
?
6.[2020浙江台州中考]用各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆体水桶水面离地面的高度为H(单位:cm),如果在离水面竖直距离为h(单位:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系为s2=4h(H-h).
应用思考:现用高度为20 cm的圆柱体塑料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距离h cm处开一个小孔.
(1)写出s2与h的关系式;并求出当h为何值时,射程s有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,求a,b之间的关系式.
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加16 cm,求垫高的高度及小孔离水面的竖直距离.
答案
6.【解析】 (1)s2=4h(H-h),
当H=20时,s2=4h(20-h)=-4(h-10)2+400,
当h=10时,s2有最大值400,此时,s有最大值20.
∴当h为10时,射程s有最大值,最大射程是20 cm.
(2)由(1)知,s2=4h(20-h),设存在a,b,使两孔射出水的射程相同,则4a(20-a)=4b(20-b),
∴20a-a2=20b-b2,a2-b2=20a-20b,
(a+b)(a-b)=20(a-b),
(a-b)(a+b-20)=0,
∴a-b=0,或a+b-20=0,
∴a=b或a+b=20.
答案
(3)设垫高的高度为m,则s2=4h(20+m-h)=-4(h-20+????2)2+(20+m)2,
∴当h=20+????2时,s最大=20+m=20+16,
∴m=16,此时h=20+????2=18,
∴垫高的高度为16 cm,小孔离水面的竖直距离为18 cm.
?
7.[2020陕西中考]如图,抛物线y=x2 +bx+c经过点(3,12)和(-2, -3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.
(1)求该抛物线的表达式;
(2)P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P,D,E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.
答案
7.【解析】 (1)由题意,得
12=9+3????+????,?3=4?2????+????,解得????=2,????=?3,
∴y=x2 +2x-3.
(2)由(1)可得,对称轴l:x=-1.
令y=0,则x2 +2x-3=0,
解得x1=-3,x2=1.
∴A(-3,0),B(1,0).
令x=0,则y=-3,∴C(0,-3),∴OA=OC=3.
∵∠PDE=∠AOC=90°,
∴当PD=DE=3时,△PDE与△AOC全等.
?
答案
设P(m,n),当点P在l右侧时,m-(-1)=3.
∴m=2,∴n=22+2×2-3=5,∴P(2,5).
∴E(-1,2)或E(-1,8).
当点P在l左侧时,由抛物线的对称性可知,P(-4,5)也满足条件.
相应的点E的坐标同上,
∴满足条件的点P的坐标为(2,5)或(-4.5),点E的坐标为(-1,2)或(-1,8).
