北师大九年级数学下册 第二章 二次函数的图像与性质复习课件(19张)
文档属性
| 名称 | 北师大九年级数学下册 第二章 二次函数的图像与性质复习课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 21:38:55 | ||
图片预览





文档简介
(共19张PPT)
第二章《二次函数》
《二次函数的图象与性质》复习
全章内容呈现
1、二次函数的定义
2、二次函数的图象与性质
3、二次函数解析式的确定
4、二次函数的应用
5、二次函数与一元二次方程
二次函数的三种常见表现形式
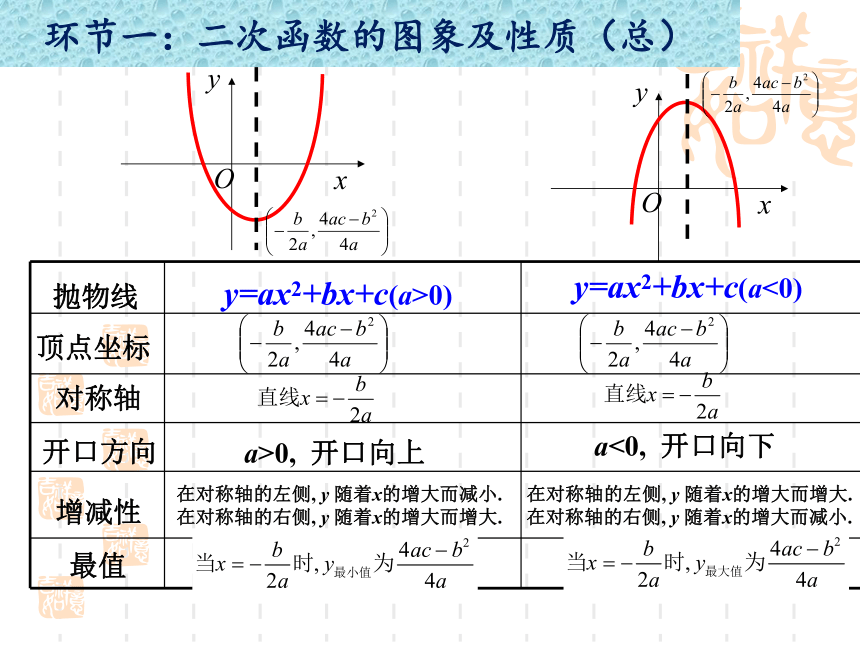
环节一:二次函数的图象及性质(总)
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
a>0,
开口向上
在对称轴的左侧,
y
随着x的增大而减小.
在对称轴的右侧,
y
随着x的增大而增大.
a<0,
开口向下
在对称轴的左侧,
y
随着x的增大而增大.
在对称轴的右侧,
y
随着x的增大而减小.
x
y
O
x
y
O
环节二:二次函数的图象及性质(分)
1、系数a的作用
(1)决定开口方向。
(2)决定开口大小。
|a|越大,抛物线的开口越小,函数值y的变化越快;
|a|越小,抛物线的开口越大,函数值y的变化越慢。
(3)a相同,形状相同;反之,形状相同,
|a|相等。
|a|相同的抛物线通过平移(或旋转)一定能重合。
(4)决定函数的最值情况。
错题呈现
(检测29页)拓展3题:
一个二次函数的图像与抛物线y=3x2的形状相同,且顶点为(1,4),那么这个函数的解析式是
。
y=±3(x-1)2+4
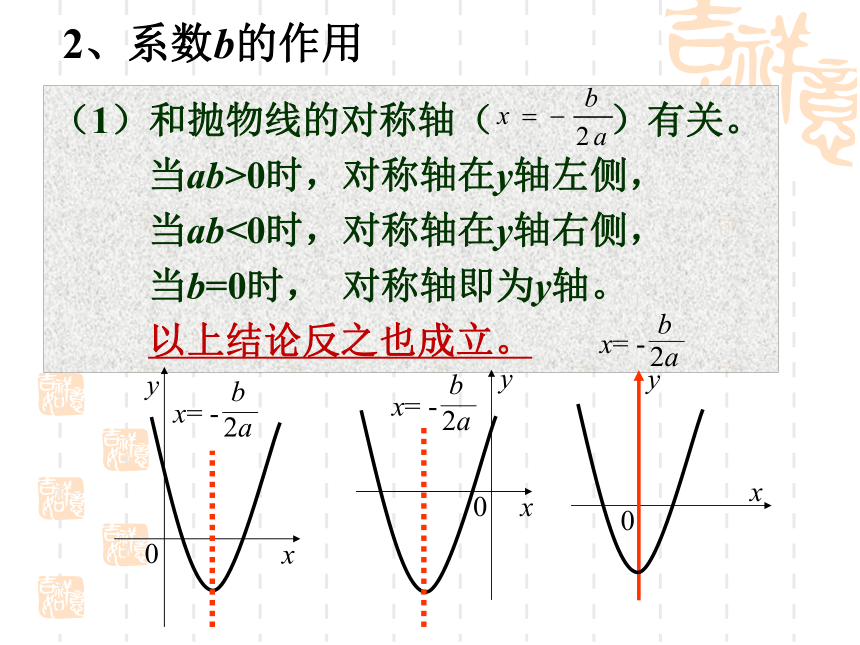
2、系数b的作用
(1)和抛物线的对称轴(
)有关。
当ab>0时,对称轴在y轴左侧,
当ab<0时,对称轴在y轴右侧,
当b=0时,
对称轴即为y轴。
以上结论反之也成立。
x
y
0
x=
-
b
2a
x
y
0
x=
-
b
2a
x
y
0
x=
-
b
2a
典例再现:检测41页2题:
①利用对程性确定交点;
(2)是二次函数增减性的分界线。
(3)根据对称性解决有关问题。
典例再现:检测35页7题:
②利用对称性解决实际问题;
7.如图所示,这是一段抛物线形状的拱梁,抛物线
的表达式为y=ax2+bx,小强骑自行车从拱梁一端
O沿直线匀速穿过拱梁部分的桥面OC.当小强骑
自行车行驶10s和26s时,拱梁的高度相同,则小
强骑自行车通过拱梁部分的桥面OC共需
s.
y
x
O
C
典例再现:检测29页6题:
③利用对称性求数量关系。
3、系数c的作用:
和y轴交点的纵坐标,任何抛物线和y轴
必有一个交点(0,c)。
当c<0时,交y轴于负半轴;
当c>0时,交y轴于正半轴;
当c=0时,图象必经过原点。
以上结论反之也成立。
y
x
?(0,c)
0
x
y
0
?(0,0)
x
y
0
?(0,c)
4、增减性
常见作用和题型:
(1)判断函数的增减性;
(2)确定函数中相关字母的范围;
例1:若二次函数y=x?-mx-1满足当x>1时,
y随x的增大而增大,则m的取值范围
是
。
(3)解决有关实际问题中的范围问题。
如课本41页“接受能力问题”。
(4)利用函数的增减性比较大小。
例2:已知抛物线y=ax2-4ax+c(a>0)
,当
x1=0,
x2=1.5,x3=3时,对应的y值依次是y1,y2,y3,
则它们之间的大小关系是
。
x
y
O
x=2
1.5
3
1
y1
y2
y3
结论:当a>0时,离对称轴
越远,函数值越大;
当a<0时,离对称轴
越近,函数值越大。
5、顶点与最值
顶点的作用:
(1)利用顶点求最值是常见的方法;
(2)顶点是函数增减性的分界点;
(3)求抛物线关于x、y轴或某点对称的抛物
线时常借助于顶点;
例3:二次函数y=-2(x-1)2+3关于x轴对称的抛物线
是
;关于y轴对称的抛物线是
;
关于原点对称的抛物线是
。
关于任意的点(m,n)对称的抛物线呢?
若是一般式y=ax2+bx+c呢?
5、顶点与最值
注意:求二次函数的最值时,要首先判断
是否在所给的自变量取值范围内,若在范围
内,常规方法求值;若不在范围内,一般要结
合图象和函数的增减性进行分析判断。
经典呈现:检测36页:5题;38页8题;39页5题。
例4:已知二次函数y=x2+4x+3,当-4≤
x
≤1时,
求y的取值范围。
变式:若改为
x
>
-5呢?如果是x
≥0呢?
6、其它
(1)几个特殊的点:
(1,a+b+c),(-1,a-b+c);
其他的呢?
(2)y=0;y>0;y<0问题(与一元二次方
程结合)
请总结本节课所学习的主要内容。
环节三:总结提升
环节四:跟踪达标
已知抛物线
y=x?+2mx+m-1.
(1)若抛物线经过坐标原点,则m_____;
(2)若抛物线与y轴交于正半轴,则m______;
(3)若抛物线的对称轴为y轴,则m______;
(4)若抛物线顶点的纵坐标最大时,m
;
(5)若当x
≤-3时,y随x的增大而减小,则m______。
=1
>
1
=0
=-0.75
≤
3
第二章《二次函数》
《二次函数的图象与性质》复习
全章内容呈现
1、二次函数的定义
2、二次函数的图象与性质
3、二次函数解析式的确定
4、二次函数的应用
5、二次函数与一元二次方程
二次函数的三种常见表现形式
环节一:二次函数的图象及性质(总)
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
a>0,
开口向上
在对称轴的左侧,
y
随着x的增大而减小.
在对称轴的右侧,
y
随着x的增大而增大.
a<0,
开口向下
在对称轴的左侧,
y
随着x的增大而增大.
在对称轴的右侧,
y
随着x的增大而减小.
x
y
O
x
y
O
环节二:二次函数的图象及性质(分)
1、系数a的作用
(1)决定开口方向。
(2)决定开口大小。
|a|越大,抛物线的开口越小,函数值y的变化越快;
|a|越小,抛物线的开口越大,函数值y的变化越慢。
(3)a相同,形状相同;反之,形状相同,
|a|相等。
|a|相同的抛物线通过平移(或旋转)一定能重合。
(4)决定函数的最值情况。
错题呈现
(检测29页)拓展3题:
一个二次函数的图像与抛物线y=3x2的形状相同,且顶点为(1,4),那么这个函数的解析式是
。
y=±3(x-1)2+4
2、系数b的作用
(1)和抛物线的对称轴(
)有关。
当ab>0时,对称轴在y轴左侧,
当ab<0时,对称轴在y轴右侧,
当b=0时,
对称轴即为y轴。
以上结论反之也成立。
x
y
0
x=
-
b
2a
x
y
0
x=
-
b
2a
x
y
0
x=
-
b
2a
典例再现:检测41页2题:
①利用对程性确定交点;
(2)是二次函数增减性的分界线。
(3)根据对称性解决有关问题。
典例再现:检测35页7题:
②利用对称性解决实际问题;
7.如图所示,这是一段抛物线形状的拱梁,抛物线
的表达式为y=ax2+bx,小强骑自行车从拱梁一端
O沿直线匀速穿过拱梁部分的桥面OC.当小强骑
自行车行驶10s和26s时,拱梁的高度相同,则小
强骑自行车通过拱梁部分的桥面OC共需
s.
y
x
O
C
典例再现:检测29页6题:
③利用对称性求数量关系。
3、系数c的作用:
和y轴交点的纵坐标,任何抛物线和y轴
必有一个交点(0,c)。
当c<0时,交y轴于负半轴;
当c>0时,交y轴于正半轴;
当c=0时,图象必经过原点。
以上结论反之也成立。
y
x
?(0,c)
0
x
y
0
?(0,0)
x
y
0
?(0,c)
4、增减性
常见作用和题型:
(1)判断函数的增减性;
(2)确定函数中相关字母的范围;
例1:若二次函数y=x?-mx-1满足当x>1时,
y随x的增大而增大,则m的取值范围
是
。
(3)解决有关实际问题中的范围问题。
如课本41页“接受能力问题”。
(4)利用函数的增减性比较大小。
例2:已知抛物线y=ax2-4ax+c(a>0)
,当
x1=0,
x2=1.5,x3=3时,对应的y值依次是y1,y2,y3,
则它们之间的大小关系是
。
x
y
O
x=2
1.5
3
1
y1
y2
y3
结论:当a>0时,离对称轴
越远,函数值越大;
当a<0时,离对称轴
越近,函数值越大。
5、顶点与最值
顶点的作用:
(1)利用顶点求最值是常见的方法;
(2)顶点是函数增减性的分界点;
(3)求抛物线关于x、y轴或某点对称的抛物
线时常借助于顶点;
例3:二次函数y=-2(x-1)2+3关于x轴对称的抛物线
是
;关于y轴对称的抛物线是
;
关于原点对称的抛物线是
。
关于任意的点(m,n)对称的抛物线呢?
若是一般式y=ax2+bx+c呢?
5、顶点与最值
注意:求二次函数的最值时,要首先判断
是否在所给的自变量取值范围内,若在范围
内,常规方法求值;若不在范围内,一般要结
合图象和函数的增减性进行分析判断。
经典呈现:检测36页:5题;38页8题;39页5题。
例4:已知二次函数y=x2+4x+3,当-4≤
x
≤1时,
求y的取值范围。
变式:若改为
x
>
-5呢?如果是x
≥0呢?
6、其它
(1)几个特殊的点:
(1,a+b+c),(-1,a-b+c);
其他的呢?
(2)y=0;y>0;y<0问题(与一元二次方
程结合)
请总结本节课所学习的主要内容。
环节三:总结提升
环节四:跟踪达标
已知抛物线
y=x?+2mx+m-1.
(1)若抛物线经过坐标原点,则m_____;
(2)若抛物线与y轴交于正半轴,则m______;
(3)若抛物线的对称轴为y轴,则m______;
(4)若抛物线顶点的纵坐标最大时,m
;
(5)若当x
≤-3时,y随x的增大而减小,则m______。
=1
>
1
=0
=-0.75
≤
3
