专题5导数之隐零点-2021届高三数学一轮复习讲义(Word版)
文档属性
| 名称 | 专题5导数之隐零点-2021届高三数学一轮复习讲义(Word版) |  | |
| 格式 | zip | ||
| 文件大小 | 370.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 20:07:27 | ||
图片预览



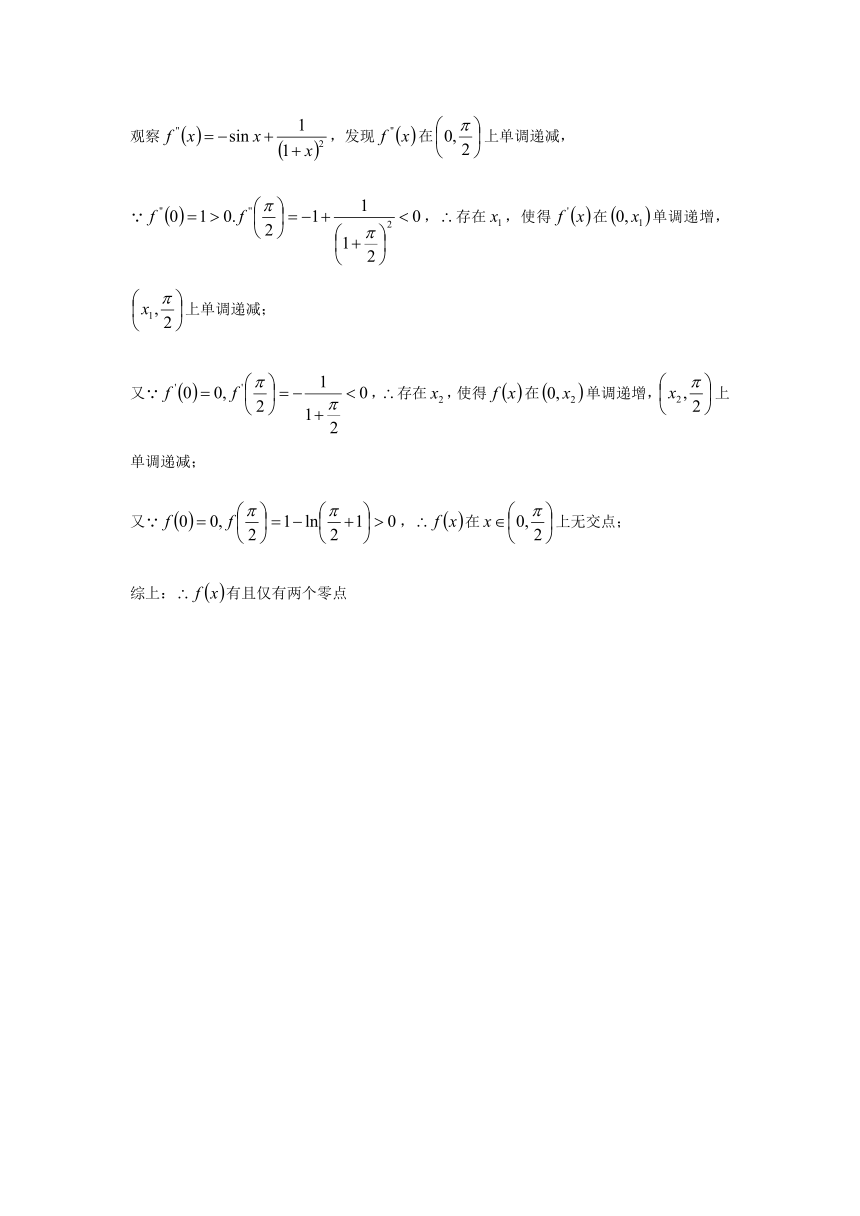
文档简介
一轮复习专题
导数之隐形零点
核心知识点:
零点存在性定理:若在上的图象是连续不断的,且是单调函数,,则在上有唯一的零点.
典型题型Ⅰ:证明函数零点个数或极值点个数(的解的个数)
解题方法:
1.确定的单调性(若无法确定的单调性,求的单调性,再往回推);2.由于零点问题就是交点问题,确定零点大概范围,再对左右进行讨论。
例:已知函数
⑴证明:存在唯一的极值点
解题思路:令
例:已知函数
⑴讨论的单调性,并证明有且仅有两个零点。
解题思路:首先确定定义域
由题意,求导得恒成立,在,上为单调递增,
,(学生可以找符合条件得其他点)
有且仅有两个零点
例:已知,函数,其中e=2.71828…为自然对数的底数.
(Ⅰ)证明:函数在上有唯一零点;
解题思路:由题意,求导,得在恒成立,在恒为单调递增函数,又,在上有唯一零点
例:已知函数,的导数,证明:
⑴在区间存在唯一极大值点;
⑵有且仅有2个零点。
解题思路:
⑴有唯一极大值,即有唯一零点
在是单调递减,且
在有唯一零点,且先增后减
在有唯一极大值点
⑵先确定零点存在范围
由图象可以看出在,,恒成立;
观察,发现在上是单调递减的,
,在上有一个交点;
观察,发现在上是单调递增的,
恒成立,在上单调递减,
在上有一个交点;
观察,发现在上单调递减,
,存在,使得在单调递增,上单调递减;
又,存在,使得在单调递增,上单调递减;
又,在上无交点;
综上:有且仅有两个零点
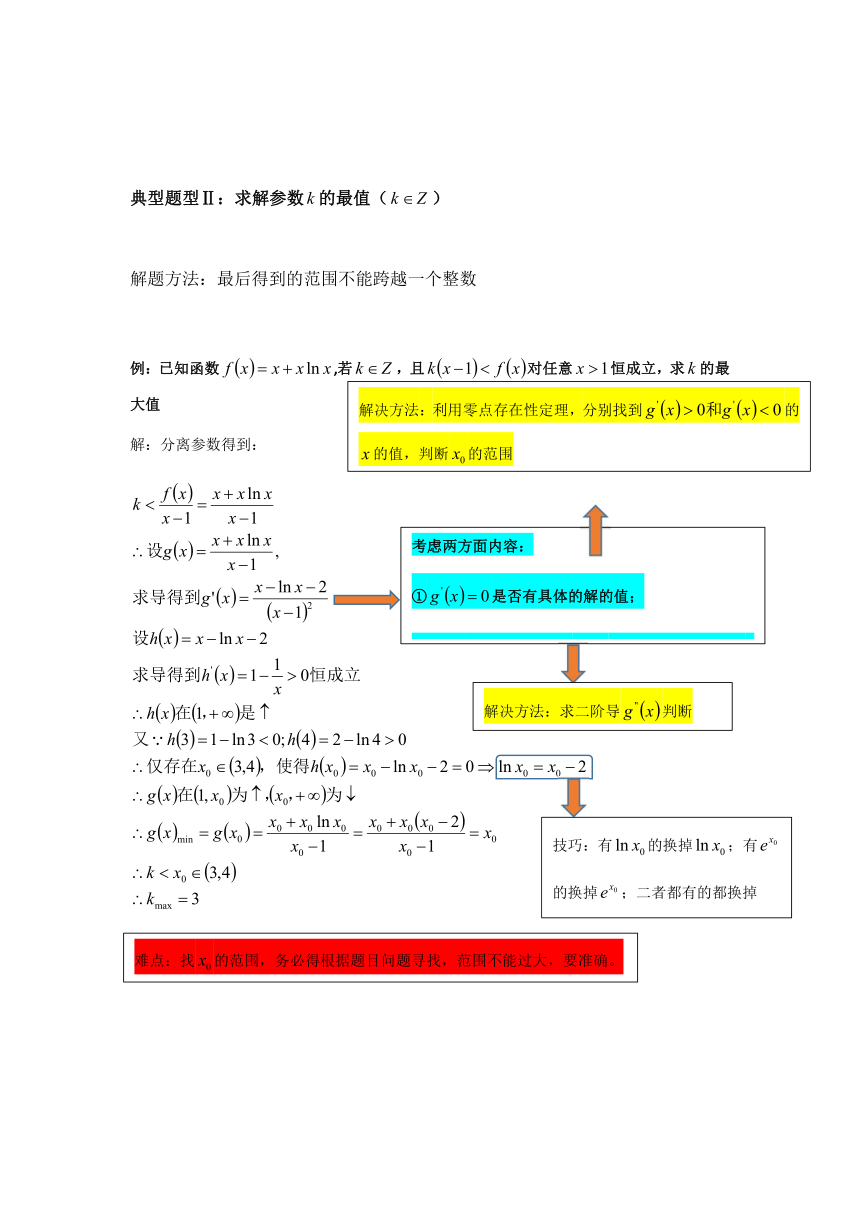
典型题型Ⅱ:求解参数的最值()
解题方法:最后得到的范围不能跨越一个整数
例:已知函数,若,且对任意恒成立,求的最大值
解:分离参数得到:
例:已知函数,若实数为整数,且对任意的时,都有恒成立,求实数的最小值
解题思路:由题意,分离参数可得,设,求导,整理得,
,设,
存在,使得,即,
在上单调递增,在上单调递减;
,
,
例:已知函数的图象在的切线方程为,若,且对任意恒成立,求的最大值
解题思路:由题意可知,
;
设,,
(这个范围可能会出现问题,但是先找出大致范围,之后再缩小范围)
存在,使得
在上单调递减,在上单调递增,
(范围跨越整数,所以利用二分法缩小范围)
,
典型题型Ⅲ:证明或求解(为极值点)取值范围
解题方法:通过结论反推范围
例:已知是函数的极值点
⑴求实数的值
⑵求证:函数存在唯一的极小值点,且(参考数据:)
解题思路:⑴由题意,求导可得,,
是的极值点,即可得
但是这里不能结束,还需要验证,因为导函数为零的点不一定是极值点。
,
,在单调递减,单调递增;
又
是的极值点,且为极大值点。
⑵由⑴可知,在单调递减,单调递增;
又(此步骤在思路上属于最后一步,空先留出来)
存在,使得,即
在单调递增,单调递减
,,
例:已知是函数的极值点
⑵求证:函数存在唯一的极小值点,且(参考数据:)
解题思路:⑵与上一道题只有范围不同,逆推可得,验证,成立。
例:已知
⑴求实数的值
⑵求证:函数存在唯一的极大值点,且
解题思路:由题意,设,若,实际上;,当是单调递减,无最小值;当时,在上是单调递减,在上是单调递增,
,,,
⑵由⑴可知,,,
,在上单调递减,在上单调递增
存在,使得,即
在单调递增,单调递减
,
另
例:已知函数
⑵当时,设函数在上的最小值为,求的值域
解题思路:由题意在上单调递增,
(这部分范围是猜测)
存在,使得,即(在这个位置验证的范围是否是,是单调递增,且,完全对上,范围成立)
,在单调递减,
例:⑴讨论的单调性,并证明当时,
⑵证明:当时,有最小值,设的最小值为,求的值域
解题思路:首先求定义域
恒成立,在上为单调递增;
若证明,即证,
成立。
⑵
存在,使得,即且为单调递减函数(同上题一样进行范围验证,成立)
,
恒成立,在单调递增,
题型Ⅳ:极值点无法确定为定值的一般求解
例:已知函数
当时,证明:
解题思路:,
设单调递增;
又
存在,使得,
在上单调递增,上单调递减
恒成立。
例:若对任意,不等式恒成立,则实数的最大值为?
解题思路:设
,当时,;
存在使得,
;
,解得
导数之隐形零点
核心知识点:
零点存在性定理:若在上的图象是连续不断的,且是单调函数,,则在上有唯一的零点.
典型题型Ⅰ:证明函数零点个数或极值点个数(的解的个数)
解题方法:
1.确定的单调性(若无法确定的单调性,求的单调性,再往回推);2.由于零点问题就是交点问题,确定零点大概范围,再对左右进行讨论。
例:已知函数
⑴证明:存在唯一的极值点
解题思路:令
例:已知函数
⑴讨论的单调性,并证明有且仅有两个零点。
解题思路:首先确定定义域
由题意,求导得恒成立,在,上为单调递增,
,(学生可以找符合条件得其他点)
有且仅有两个零点
例:已知,函数,其中e=2.71828…为自然对数的底数.
(Ⅰ)证明:函数在上有唯一零点;
解题思路:由题意,求导,得在恒成立,在恒为单调递增函数,又,在上有唯一零点
例:已知函数,的导数,证明:
⑴在区间存在唯一极大值点;
⑵有且仅有2个零点。
解题思路:
⑴有唯一极大值,即有唯一零点
在是单调递减,且
在有唯一零点,且先增后减
在有唯一极大值点
⑵先确定零点存在范围
由图象可以看出在,,恒成立;
观察,发现在上是单调递减的,
,在上有一个交点;
观察,发现在上是单调递增的,
恒成立,在上单调递减,
在上有一个交点;
观察,发现在上单调递减,
,存在,使得在单调递增,上单调递减;
又,存在,使得在单调递增,上单调递减;
又,在上无交点;
综上:有且仅有两个零点
典型题型Ⅱ:求解参数的最值()
解题方法:最后得到的范围不能跨越一个整数
例:已知函数,若,且对任意恒成立,求的最大值
解:分离参数得到:
例:已知函数,若实数为整数,且对任意的时,都有恒成立,求实数的最小值
解题思路:由题意,分离参数可得,设,求导,整理得,
,设,
存在,使得,即,
在上单调递增,在上单调递减;
,
,
例:已知函数的图象在的切线方程为,若,且对任意恒成立,求的最大值
解题思路:由题意可知,
;
设,,
(这个范围可能会出现问题,但是先找出大致范围,之后再缩小范围)
存在,使得
在上单调递减,在上单调递增,
(范围跨越整数,所以利用二分法缩小范围)
,
典型题型Ⅲ:证明或求解(为极值点)取值范围
解题方法:通过结论反推范围
例:已知是函数的极值点
⑴求实数的值
⑵求证:函数存在唯一的极小值点,且(参考数据:)
解题思路:⑴由题意,求导可得,,
是的极值点,即可得
但是这里不能结束,还需要验证,因为导函数为零的点不一定是极值点。
,
,在单调递减,单调递增;
又
是的极值点,且为极大值点。
⑵由⑴可知,在单调递减,单调递增;
又(此步骤在思路上属于最后一步,空先留出来)
存在,使得,即
在单调递增,单调递减
,,
例:已知是函数的极值点
⑵求证:函数存在唯一的极小值点,且(参考数据:)
解题思路:⑵与上一道题只有范围不同,逆推可得,验证,成立。
例:已知
⑴求实数的值
⑵求证:函数存在唯一的极大值点,且
解题思路:由题意,设,若,实际上;,当是单调递减,无最小值;当时,在上是单调递减,在上是单调递增,
,,,
⑵由⑴可知,,,
,在上单调递减,在上单调递增
存在,使得,即
在单调递增,单调递减
,
另
例:已知函数
⑵当时,设函数在上的最小值为,求的值域
解题思路:由题意在上单调递增,
(这部分范围是猜测)
存在,使得,即(在这个位置验证的范围是否是,是单调递增,且,完全对上,范围成立)
,在单调递减,
例:⑴讨论的单调性,并证明当时,
⑵证明:当时,有最小值,设的最小值为,求的值域
解题思路:首先求定义域
恒成立,在上为单调递增;
若证明,即证,
成立。
⑵
存在,使得,即且为单调递减函数(同上题一样进行范围验证,成立)
,
恒成立,在单调递增,
题型Ⅳ:极值点无法确定为定值的一般求解
例:已知函数
当时,证明:
解题思路:,
设单调递增;
又
存在,使得,
在上单调递增,上单调递减
恒成立。
例:若对任意,不等式恒成立,则实数的最大值为?
解题思路:设
,当时,;
存在使得,
;
,解得
同课章节目录
