【A典学案】二次函数-章末复习 课件(26张PPT)
文档属性
| 名称 | 【A典学案】二次函数-章末复习 课件(26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 16:23:38 | ||
图片预览








文档简介
(共28张PPT)
第二章 二次函数
第19课时 章末复习
北师大版 九年级下册
内容分析
二次函数图象和性质体现了数形结合的数学思想,对同学们基本数学思想和素养的形成起到了推动作用,它是对我们所学知识的应用和提高.学习的重点是理解二次函数的概念,掌握二次函数的图象和性质, 理解二次函数与一元二次方程的关系;难点是应用二次函数解决实际问题.
知识链接
1.用描点法画函数图象的一般步骤是:____,____,____.
2.一般地,形如 y=kx+b(k,b 是常数,k____0)的函数,叫做____函数.
3.一元二次方程 的根的情况与根的判别式
“ ”的关系:
① >0 , 方程有 ____ 的实数根;
② =0 ,方程有____的实数根;
③ <0,方程_____实数根.
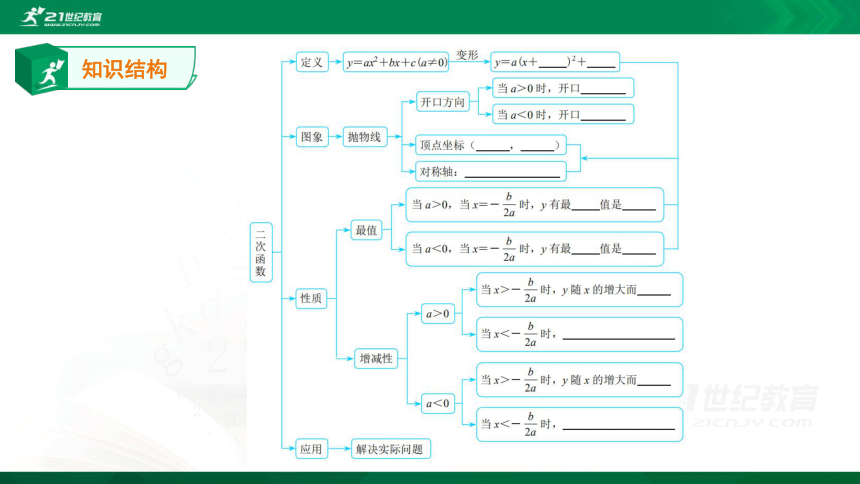
知识结构
典例精讲
类型之一 二次函数的概念
【例 1】用一根长为 800 cm 的木条做一个长方形的窗框,若宽为 x cm,写出它的面积 y 与 x 之间的函数关系式,并判断 y 是 x 的二次函数吗?
解析:设宽为x cm,由题意得,矩形的周长为800 cm,
∴矩形的长为 cm.
∴
y是x的二次函数.
典例精讲
类型之二 二次函数的图象和性质
【例 2】已知二次函数 .
(1)将 化成 的形式;
(2)求该二次函数的图象的对称轴和顶点坐标;
(3)当 x 取何值时,y 随 x 的增大而减小?
典例精讲
解析:(1) .
(2)二次函数的图象的对称轴是直线x=3,顶点坐标是(3,-4).
(3)∵抛物线的开口向上,对称轴是直线x=3,
∴当x≤3时,y随x的增大而减小.
典例精讲
类型之三 确定二次函数表达式
【例 3】关于 x 的二次函数 经过点 A(-3,0),点 C(0,3),点 D 为二次函数的顶点,DE 为二次函数的对称轴,E 在 x 轴上.
(1)求抛物线的表达式;
(2)DE 上是否存在点 P 到 AD 的距离与到 x 轴的距离相等? 若存在,请求出 P 点的坐标;若不存在,请说明理由.
典例精讲
解析:(1)把A(-3,0),C(0,3)代入
得-9-3b+c=0,c=3,解得b=-2,c=3,
∴抛物线表达式为
(2)存在.
如图,连接AD作PH⊥AD于H,
∴抛物线的对称轴为直线x=-1,
A
2
1
3
4
O
1
B
x
y
-1
-2
-3
E
H
P
C
D
典例精讲
D(-1,4),E(-1,0).
∴AD=
设P(-1,t),则PE=PH=t,DP=4-t,
∵∠PDH=∠ADE,∴Rt△DPH∽Rt△DAE.
解得t= .
∴P点坐标为(-1, ).
典例精讲
类型之四 二次函数和一元二次方程的关系
【例 4】已知函数 (m 是常数).
(1)求证:不论 m 为何值,该函数的图象都经过 y 轴上的一个定点;
(2)若该函数的图象与 x 轴只有一个交点,求 m 的值.
典例精讲
解析:(1)证明:当x=0时,y=1.
∴不论m为何值,函数 的图象都经过y轴上的一个定点(0,1)
(2)解:①当m=0时,函数 的图象与x轴只有一个交点;
②当m≠0时,若函数 的图象与x轴只有一个交点,则方程
有两个相等的实数根,
,m=9.
综上,若函数 的图象与x轴只有一个交点,则m的值为0或9.
典例精讲
类型之五 二次函数的应用
【例 5】某商店销售一种成本为 40 元/kg 的水产品,若按 50 元/kg 销售,一个月可售出 500 kg,售价每涨 1 元,月销售量就减少 10 kg.
(1)写出月销售利润 y(元)与售价 x(元/kg)之间的函数表达式;
(2)当售价定为多少元时,该商店月销售利润为 8000 元?
(3)当售价定为多少元时会获得最大利润?求出最大利润.
典例精讲
解析:(1)可卖出千克数为500-10(x-50)=1000-10x,
y与x的函数表达式为y=(x-40)(1000-10x)
(2)根据题意得 ,解得x=60或x=80.
当售价定为60元或80元时,该商店月销售利润为8000元.
(3)∵y=(x-40)[500-10(x-50)]=
∴当x=70时,利润最大为9000元.
∴当售价为70元时,最大利润是9000元.
课堂操练
1.对抛物线 而言, 下列结论正确的是( )
A.与 x 轴有两个交点
B.开口向上
C.与 y 轴的交点坐标是(0,3)
D.顶点坐标是(1,-2)
D
课堂操练
2.二次函数 的图象可以由二次函数 的图象平移而得到,下列平移正确的是( )
A.先向左平移 2 个单位,在向上平移 1 个单位
B.先向左平移 2 个单位,在向下平移 1 个单位
C.先向右平移 2 个单位,在向上平移 1 个单位
D.先向右平移 2 个单位,在向下平移 1 个单位
B
课堂操练
3.二次函数 的图象如图所示.当 y<0 时,自变量 x 的取值范围是( )
A.-1<x<3 B.x<-1
C.x>3 D.x<-1 或 x>3
4.点 是二次函数 的图象上两点,则 与 的大小关系为 _____ (填“>”、“<”、“=”).
A
<
课堂操练
5.如图,已知二次函数 的图象经过点 A(-1,0),B(1,-2),该图象与 x 轴的另一个交点为 C,则 AC 长为________.
3
课堂操练
6.已知二次函数 的图象如图所示,现有下列结论:① ,②a>0,③b>0,④c>0,⑤9a+3b+c<0,则其中结论正确的个数有_________个.
3
课堂操练
7.已知二次函数的图象以 A(3,-1)为顶点,且经过点(2,3).
(1)求抛物线的解析式;
(2)若函数 y 随 x 的增大而减小,求出此时 x 的取值范围.
课堂操练
解析:(1)∵抛物线的顶点坐标为(3,-1),
∴可设抛物线的解析式为
又∵经过点(2,3),
∴
解得a=4.
∴抛物线的解析式为 .
(2)由①知x≤3.
课堂操练
8.如图所示,二次函数 的图象与 x 轴的一个交点为 A(3,0),另一个交点为 B,且与 y轴交于点 C.
(1)求 m 的值;
(2)求点 B 的坐标;
(3)该二次函数图象上有一点 D(x,y)(其中 x>0,y>0),使
,求点 D 的坐标.
课堂操练
解析:(1)∵ 的图象与x轴的一个交点为A(3,0),∴0= .∴m=3.
(2)把m=3代入 ,得
令y=0,即 .
解得
∴点B的坐标为(-1,0).
(3)∵ ,点D在第一象限,
课堂操练
∴点C,D关于二次函数对称轴对称.
由二次函数解析式可得其对称轴为x=1,点C的坐标为(0,3),
∴点D的坐标为(2,3).
中考在线
(杭州)设二次函数 ( 是实数).
(1)甲求得当 x=0 时,y=0;当 x=1时,y=0;乙求得当 x= 时,y=- .若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.
(2)写出二次函数图象的对称轴,并求该函数的最小值(用含 的代数式表示).
中考在线
解析:(1)当x=0时,y=0;当x=1时,y=0;
∴二次函数经过点(0,0),(1,0),
∴
∴y=x(x-1)=
当x= 时,y=- ,
∴乙说的不对;
(2)对称轴为x=
当x= 时,y=- 是函数的最小值.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第二章 二次函数
第19课时 章末复习
北师大版 九年级下册
内容分析
二次函数图象和性质体现了数形结合的数学思想,对同学们基本数学思想和素养的形成起到了推动作用,它是对我们所学知识的应用和提高.学习的重点是理解二次函数的概念,掌握二次函数的图象和性质, 理解二次函数与一元二次方程的关系;难点是应用二次函数解决实际问题.
知识链接
1.用描点法画函数图象的一般步骤是:____,____,____.
2.一般地,形如 y=kx+b(k,b 是常数,k____0)的函数,叫做____函数.
3.一元二次方程 的根的情况与根的判别式
“ ”的关系:
① >0 , 方程有 ____ 的实数根;
② =0 ,方程有____的实数根;
③ <0,方程_____实数根.
知识结构
典例精讲
类型之一 二次函数的概念
【例 1】用一根长为 800 cm 的木条做一个长方形的窗框,若宽为 x cm,写出它的面积 y 与 x 之间的函数关系式,并判断 y 是 x 的二次函数吗?
解析:设宽为x cm,由题意得,矩形的周长为800 cm,
∴矩形的长为 cm.
∴
y是x的二次函数.
典例精讲
类型之二 二次函数的图象和性质
【例 2】已知二次函数 .
(1)将 化成 的形式;
(2)求该二次函数的图象的对称轴和顶点坐标;
(3)当 x 取何值时,y 随 x 的增大而减小?
典例精讲
解析:(1) .
(2)二次函数的图象的对称轴是直线x=3,顶点坐标是(3,-4).
(3)∵抛物线的开口向上,对称轴是直线x=3,
∴当x≤3时,y随x的增大而减小.
典例精讲
类型之三 确定二次函数表达式
【例 3】关于 x 的二次函数 经过点 A(-3,0),点 C(0,3),点 D 为二次函数的顶点,DE 为二次函数的对称轴,E 在 x 轴上.
(1)求抛物线的表达式;
(2)DE 上是否存在点 P 到 AD 的距离与到 x 轴的距离相等? 若存在,请求出 P 点的坐标;若不存在,请说明理由.
典例精讲
解析:(1)把A(-3,0),C(0,3)代入
得-9-3b+c=0,c=3,解得b=-2,c=3,
∴抛物线表达式为
(2)存在.
如图,连接AD作PH⊥AD于H,
∴抛物线的对称轴为直线x=-1,
A
2
1
3
4
O
1
B
x
y
-1
-2
-3
E
H
P
C
D
典例精讲
D(-1,4),E(-1,0).
∴AD=
设P(-1,t),则PE=PH=t,DP=4-t,
∵∠PDH=∠ADE,∴Rt△DPH∽Rt△DAE.
解得t= .
∴P点坐标为(-1, ).
典例精讲
类型之四 二次函数和一元二次方程的关系
【例 4】已知函数 (m 是常数).
(1)求证:不论 m 为何值,该函数的图象都经过 y 轴上的一个定点;
(2)若该函数的图象与 x 轴只有一个交点,求 m 的值.
典例精讲
解析:(1)证明:当x=0时,y=1.
∴不论m为何值,函数 的图象都经过y轴上的一个定点(0,1)
(2)解:①当m=0时,函数 的图象与x轴只有一个交点;
②当m≠0时,若函数 的图象与x轴只有一个交点,则方程
有两个相等的实数根,
,m=9.
综上,若函数 的图象与x轴只有一个交点,则m的值为0或9.
典例精讲
类型之五 二次函数的应用
【例 5】某商店销售一种成本为 40 元/kg 的水产品,若按 50 元/kg 销售,一个月可售出 500 kg,售价每涨 1 元,月销售量就减少 10 kg.
(1)写出月销售利润 y(元)与售价 x(元/kg)之间的函数表达式;
(2)当售价定为多少元时,该商店月销售利润为 8000 元?
(3)当售价定为多少元时会获得最大利润?求出最大利润.
典例精讲
解析:(1)可卖出千克数为500-10(x-50)=1000-10x,
y与x的函数表达式为y=(x-40)(1000-10x)
(2)根据题意得 ,解得x=60或x=80.
当售价定为60元或80元时,该商店月销售利润为8000元.
(3)∵y=(x-40)[500-10(x-50)]=
∴当x=70时,利润最大为9000元.
∴当售价为70元时,最大利润是9000元.
课堂操练
1.对抛物线 而言, 下列结论正确的是( )
A.与 x 轴有两个交点
B.开口向上
C.与 y 轴的交点坐标是(0,3)
D.顶点坐标是(1,-2)
D
课堂操练
2.二次函数 的图象可以由二次函数 的图象平移而得到,下列平移正确的是( )
A.先向左平移 2 个单位,在向上平移 1 个单位
B.先向左平移 2 个单位,在向下平移 1 个单位
C.先向右平移 2 个单位,在向上平移 1 个单位
D.先向右平移 2 个单位,在向下平移 1 个单位
B
课堂操练
3.二次函数 的图象如图所示.当 y<0 时,自变量 x 的取值范围是( )
A.-1<x<3 B.x<-1
C.x>3 D.x<-1 或 x>3
4.点 是二次函数 的图象上两点,则 与 的大小关系为 _____ (填“>”、“<”、“=”).
A
<
课堂操练
5.如图,已知二次函数 的图象经过点 A(-1,0),B(1,-2),该图象与 x 轴的另一个交点为 C,则 AC 长为________.
3
课堂操练
6.已知二次函数 的图象如图所示,现有下列结论:① ,②a>0,③b>0,④c>0,⑤9a+3b+c<0,则其中结论正确的个数有_________个.
3
课堂操练
7.已知二次函数的图象以 A(3,-1)为顶点,且经过点(2,3).
(1)求抛物线的解析式;
(2)若函数 y 随 x 的增大而减小,求出此时 x 的取值范围.
课堂操练
解析:(1)∵抛物线的顶点坐标为(3,-1),
∴可设抛物线的解析式为
又∵经过点(2,3),
∴
解得a=4.
∴抛物线的解析式为 .
(2)由①知x≤3.
课堂操练
8.如图所示,二次函数 的图象与 x 轴的一个交点为 A(3,0),另一个交点为 B,且与 y轴交于点 C.
(1)求 m 的值;
(2)求点 B 的坐标;
(3)该二次函数图象上有一点 D(x,y)(其中 x>0,y>0),使
,求点 D 的坐标.
课堂操练
解析:(1)∵ 的图象与x轴的一个交点为A(3,0),∴0= .∴m=3.
(2)把m=3代入 ,得
令y=0,即 .
解得
∴点B的坐标为(-1,0).
(3)∵ ,点D在第一象限,
课堂操练
∴点C,D关于二次函数对称轴对称.
由二次函数解析式可得其对称轴为x=1,点C的坐标为(0,3),
∴点D的坐标为(2,3).
中考在线
(杭州)设二次函数 ( 是实数).
(1)甲求得当 x=0 时,y=0;当 x=1时,y=0;乙求得当 x= 时,y=- .若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.
(2)写出二次函数图象的对称轴,并求该函数的最小值(用含 的代数式表示).
中考在线
解析:(1)当x=0时,y=0;当x=1时,y=0;
∴二次函数经过点(0,0),(1,0),
∴
∴y=x(x-1)=
当x= 时,y=- ,
∴乙说的不对;
(2)对称轴为x=
当x= 时,y=- 是函数的最小值.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
