2.2 第4课时 二次函数y=a(x-h)2+k的图象与性质 课件(共36张PPT)
文档属性
| 名称 | 2.2 第4课时 二次函数y=a(x-h)2+k的图象与性质 课件(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 07:30:32 | ||
图片预览



文档简介
(共36张PPT)
第二章
二次函数
2.2
二次函数的图象与性质
第4课时
二次函数y=a(x-h)2+k的图象与性质
北师大版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
1.会用描点法画出y=a(x-h)2+k
(a
≠0)的图象.
2.掌握二次函数y=a(x-h)2+k
(a
≠0)的图象的性质并会应用.(重点)
3.理解二次函数y=a(x-h)2+k
(a
≠0)与y=ax2
(a
≠0)之间的联系.(难点)
情景导学
2
情景导学
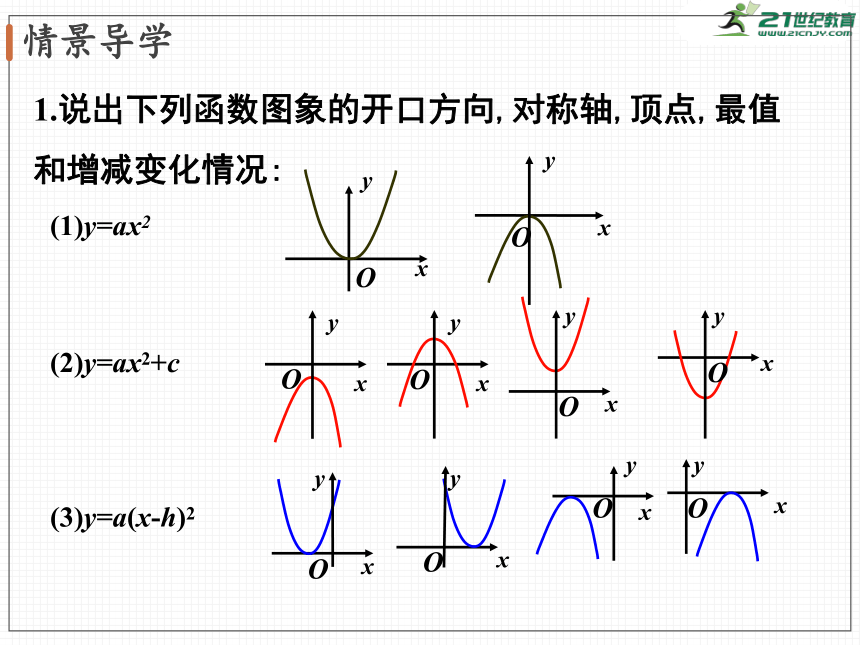
1.说出下列函数图象的开口方向,对称轴,顶点,最值和增减变化情况:
(1)y=ax2
(2)y=ax2+c
(3)y=a(x-h)2
y
y
y
y
x
x
x
x
O
O
O
O
y
y
y
y
x
x
x
x
O
O
O
O
y
y
x
x
O
O
情景导学
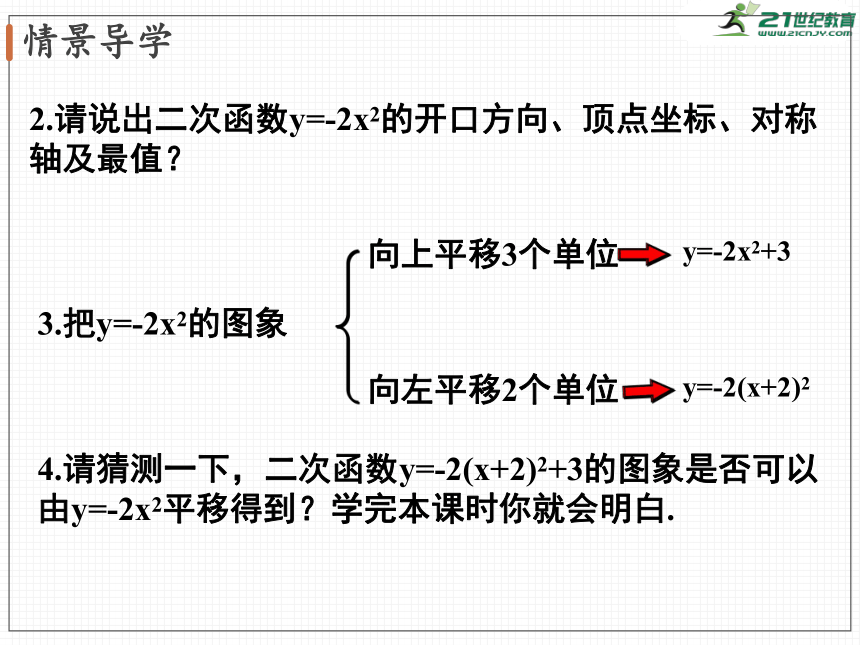
2.请说出二次函数y=-2x2的开口方向、顶点坐标、对称轴及最值?
3.把y=-2x2的图象
向上平移3个单位
y=-2x2+3
向左平移2个单位
y=-2(x+2)2
4.请猜测一下,二次函数y=-2(x+2)2+3的图象是否可以由y=-2x2平移得到?学完本课时你就会明白.
新课进行时
3
新课进行时
核心知识点一
二次函数y=a(x-h)2+k的图象和性质
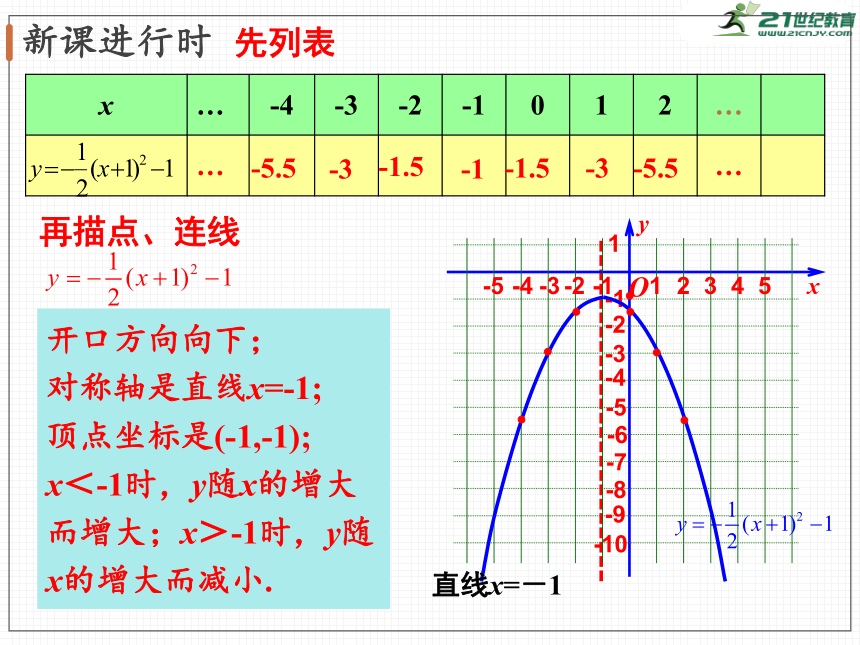
1.画出函数
的图象.指出它的开口方向、顶点、对称轴与增减性.
合作探究
新课进行时
…
…
…
…
2
1
0
-1
-2
-3
-4
x
先列表
再描点、连线
-5.5
-3
-1.5
-1
-1.5
-3
-5.5
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
直线x=-1
开口方向向下;
对称轴是直线x=-1;
顶点坐标是(-1,-1);
x<-1时,y随x的增大而增大;x>-1时,y随x的增大而减小.
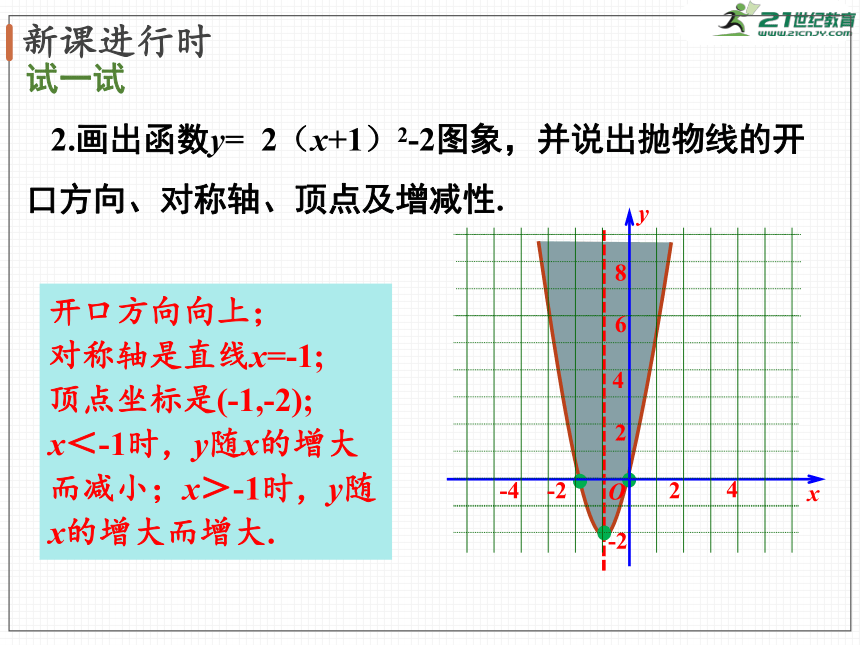
试一试
2.画出函数y=
2(x+1)2-2图象,并说出抛物线的开口方向、对称轴、顶点及增减性.
开口方向向上;
对称轴是直线x=-1;
顶点坐标是(-1,-2);
x<-1时,y随x的增大而减小;x>-1时,y随x的增大而增大.
-2
2
x
y
O
-2
4
6
8
-4
2
4
新课进行时
新课进行时
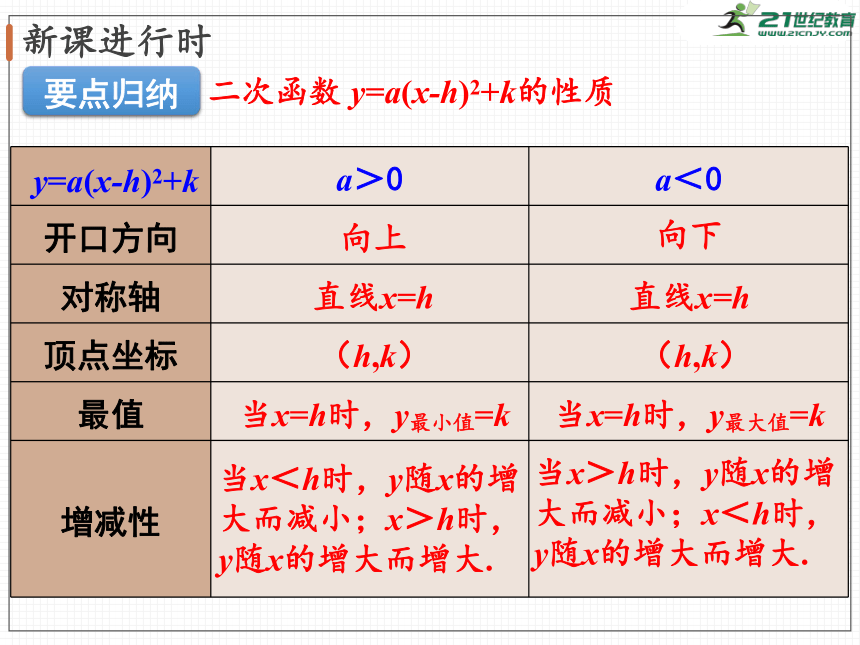
二次函数
y=a(x-h)2+k的性质
y=a(x-h)2+k
a>0
a<0
开口方向
对称轴
顶点坐标
最值
增减性
要点归纳
向上
向下
直线x=h
直线x=h
(h,k)
(h,k)
当x=h时,y最小值=k
当x=h时,y最大值=k
当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;x<h时,y随x的增大而增大.
顶点式
新课进行时
例1.已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
解析:根据二次函数开口向上则a>0,根据-c是二次函数顶点坐标的纵坐标,得出c>0,故一次函数y=ax+c的大致图象经过第一、二、三象限.故选A.
典例精析
A
新课进行时
例2.
已知二次函数y=a(x-1)2-4的图象经过点(3,0).
(1)求a的值;
(2)若A(m,y1)、B(m+n,y2)(n>0)是该函数图象上的两点,当y1=y
2时,求m、n之间的数量关系.
解:(1)将(3,0)代入y=a(x-1)2-4,
得0=4a-4,解得a=1;
(2)方法一:
根据题意,得y1=(m-1)2-4,y2=(m+n-1)2-4,
∵y1=y2,
∴(m-1)2-4=(m+n-1)2-4,即(m-1)2=(m+n-1)2.
∵n>0,∴m-1=-(m+n-1),化简,得2m+n=2;
新课进行时
方法二:
∵函数y=(x-1)2-4的图象的对称轴是经过点(1,-4),且平行于y轴的直线,
∴m+n-1=1-m,化简,得2m+n=2.
新课进行时
向左平移
1个单位
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
合作探究
怎样移动抛物线
就可以得到抛物线
?
平移方法1
向下平移
1个单位
新课进行时
核心知识点二
二次函数y=a(x-h)2+k与y=ax2的关系
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
怎样移动抛物线
就可以得到抛物线
?
平移方法2
向左平移
1个单位
向下平移
1个单位
新课进行时
要点归纳
二次函数y=ax2
与y=a(x-h)2+k的关系
可以看作互相平移得到的(h>0,k>0).
y
=
ax2
y
=
ax2
+
k
y
=
a(x
-
h
)2
y
=
a(
x
-
h
)2
+
k
上下
平移
左右
平移
上下
平移
左右
平移
平移规律
简记为:
上下平移,
括号外上加下减;
左右平移,
括号内左加右减.
二次项系数a不变.
新课进行时
1.请回答抛物线y
=
4(x-3)2+7由抛物线y=4x2怎样平移得到?
由抛物线向上平移7个单位再向右平移3个单位得到的.
2.如果一条抛物线的形状与
形状相同,且顶点坐标是(4,-2),试求这个函数关系式.
练一练
新课进行时
知识小结
4
知识小结
一般地,抛物线
y
=
a(x-h)2+k与y
=
ax2形状相同,位置不同.
二次函数y=a(x-h)2+k的图象和性质
图象特点
当a>0,开口向上;当a<0,开口向下.
对称轴是x=h,
顶点坐标是(h,k).
平移规律
左右平移:括号内左加右减;
上下平移:括号外上加下减.
随堂演练
5
随堂演练
二次函数
开口方向
对称轴
顶点坐标
y=2(x+3)2+5
向上
(
1,
-2
)
向下
向下
(
3
,
7)
(
2
,
-6
)
向上
直线x=-3
直线x=1
直线x=3
直线x=2
(-3,
5
)
y=-3(x-1)2-2
y
=
4(x-3)2+7
y=-5(2-x)2-6
1.完成下列表格:
2.抛物线y=-3x2+2的图象向右平移2个单位,再向上平移1个单位,得到抛物线的解析式为______________
3.抛物线y=2x2不动,把x轴、y轴分别向上、向左平移3个单位,则在新坐标系下,此抛物线的解析式为__________________.
y=2(x-3)2-3
随堂演练
4.已知y=
(x-3)2-2的部分图象如图所示,抛物线与x轴交点的一个坐标是(1,0),则另一个交点的坐标是________.
解析:由抛物线的对称性知,对称轴为x=3,一个交点坐标是(1,0),
则另一个交点坐标是(5,0).
(5,0)
随堂演练
5.对于抛物线y=-
(x?2)2+6,下列结论:①抛物线的开口向下;②对称轴为直线x=2;③顶点坐标为(2,6);④当x>2时,y随x的增大而减小.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
D
随堂演练
6.已知点A(x1,y1)、B(x2,y2)在二次函数
y=-(x-1)2+1的图象上,若-1<x1<0,3<x2<4,则y1_____y2(填“>”、“<”或“=”).
>
解析:抛物线y=-(x-1)2+1的对称轴为直线x=1,
∵a=-1<0,
∴抛物线开口向下,
∵-1<x1<0,3<x2<4,
∴y1>y2.
随堂演练
7.抛物线
与x轴交于B,C两点,顶点为A,则△ABC的周长为(
)
A.
B.
C.12
D.
B
随堂演练
8.如图,在平面直角坐标系xOy中,抛物线y=x2向左平移1个单位,再向下平移4个单位,得到抛物线y=(x-h)2+k.所得抛物线与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
(1)求h,k的值;
解:(1)∵将抛物线y=x2向左平移1个单位,再向下平移4个单位,得到抛物线y=(x+1)2-4,
∴h=-1,k=-4;
随堂演练
(2)判断△ACD的形状,并说明理由.
(2)△ACD为直角三角形.
理由如下:由(1)得y=(x+1)2-4.
当y=0时,(x+1)2-4=0,x=-3或x=1,
∴A(-3,0),B(1,0).
当x=0时,y=(x+1)2-4=(0+1)2-4=-3,
∴C点坐标为(0,-3).
顶点坐标为D(-1,-4).
随堂演练
作出抛物线的对称轴x=-1交x轴于点E,过D作DF⊥y轴于点F,如图所示.
在Rt△AED中,AD2=22+42=20;
在Rt△AOC中,AC2=32+32=18;
在Rt△CFD中,CD2=12+12=2.
∵AC2+CD2=AD2,
∴△ACD是直角三角形.
随堂演练
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第二章
二次函数
2.2
二次函数的图象与性质
第4课时
二次函数y=a(x-h)2+k的图象与性质
北师大版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
1.会用描点法画出y=a(x-h)2+k
(a
≠0)的图象.
2.掌握二次函数y=a(x-h)2+k
(a
≠0)的图象的性质并会应用.(重点)
3.理解二次函数y=a(x-h)2+k
(a
≠0)与y=ax2
(a
≠0)之间的联系.(难点)
情景导学
2
情景导学
1.说出下列函数图象的开口方向,对称轴,顶点,最值和增减变化情况:
(1)y=ax2
(2)y=ax2+c
(3)y=a(x-h)2
y
y
y
y
x
x
x
x
O
O
O
O
y
y
y
y
x
x
x
x
O
O
O
O
y
y
x
x
O
O
情景导学
2.请说出二次函数y=-2x2的开口方向、顶点坐标、对称轴及最值?
3.把y=-2x2的图象
向上平移3个单位
y=-2x2+3
向左平移2个单位
y=-2(x+2)2
4.请猜测一下,二次函数y=-2(x+2)2+3的图象是否可以由y=-2x2平移得到?学完本课时你就会明白.
新课进行时
3
新课进行时
核心知识点一
二次函数y=a(x-h)2+k的图象和性质
1.画出函数
的图象.指出它的开口方向、顶点、对称轴与增减性.
合作探究
新课进行时
…
…
…
…
2
1
0
-1
-2
-3
-4
x
先列表
再描点、连线
-5.5
-3
-1.5
-1
-1.5
-3
-5.5
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
直线x=-1
开口方向向下;
对称轴是直线x=-1;
顶点坐标是(-1,-1);
x<-1时,y随x的增大而增大;x>-1时,y随x的增大而减小.
试一试
2.画出函数y=
2(x+1)2-2图象,并说出抛物线的开口方向、对称轴、顶点及增减性.
开口方向向上;
对称轴是直线x=-1;
顶点坐标是(-1,-2);
x<-1时,y随x的增大而减小;x>-1时,y随x的增大而增大.
-2
2
x
y
O
-2
4
6
8
-4
2
4
新课进行时
新课进行时
二次函数
y=a(x-h)2+k的性质
y=a(x-h)2+k
a>0
a<0
开口方向
对称轴
顶点坐标
最值
增减性
要点归纳
向上
向下
直线x=h
直线x=h
(h,k)
(h,k)
当x=h时,y最小值=k
当x=h时,y最大值=k
当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;x<h时,y随x的增大而增大.
顶点式
新课进行时
例1.已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
解析:根据二次函数开口向上则a>0,根据-c是二次函数顶点坐标的纵坐标,得出c>0,故一次函数y=ax+c的大致图象经过第一、二、三象限.故选A.
典例精析
A
新课进行时
例2.
已知二次函数y=a(x-1)2-4的图象经过点(3,0).
(1)求a的值;
(2)若A(m,y1)、B(m+n,y2)(n>0)是该函数图象上的两点,当y1=y
2时,求m、n之间的数量关系.
解:(1)将(3,0)代入y=a(x-1)2-4,
得0=4a-4,解得a=1;
(2)方法一:
根据题意,得y1=(m-1)2-4,y2=(m+n-1)2-4,
∵y1=y2,
∴(m-1)2-4=(m+n-1)2-4,即(m-1)2=(m+n-1)2.
∵n>0,∴m-1=-(m+n-1),化简,得2m+n=2;
新课进行时
方法二:
∵函数y=(x-1)2-4的图象的对称轴是经过点(1,-4),且平行于y轴的直线,
∴m+n-1=1-m,化简,得2m+n=2.
新课进行时
向左平移
1个单位
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
合作探究
怎样移动抛物线
就可以得到抛物线
?
平移方法1
向下平移
1个单位
新课进行时
核心知识点二
二次函数y=a(x-h)2+k与y=ax2的关系
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
怎样移动抛物线
就可以得到抛物线
?
平移方法2
向左平移
1个单位
向下平移
1个单位
新课进行时
要点归纳
二次函数y=ax2
与y=a(x-h)2+k的关系
可以看作互相平移得到的(h>0,k>0).
y
=
ax2
y
=
ax2
+
k
y
=
a(x
-
h
)2
y
=
a(
x
-
h
)2
+
k
上下
平移
左右
平移
上下
平移
左右
平移
平移规律
简记为:
上下平移,
括号外上加下减;
左右平移,
括号内左加右减.
二次项系数a不变.
新课进行时
1.请回答抛物线y
=
4(x-3)2+7由抛物线y=4x2怎样平移得到?
由抛物线向上平移7个单位再向右平移3个单位得到的.
2.如果一条抛物线的形状与
形状相同,且顶点坐标是(4,-2),试求这个函数关系式.
练一练
新课进行时
知识小结
4
知识小结
一般地,抛物线
y
=
a(x-h)2+k与y
=
ax2形状相同,位置不同.
二次函数y=a(x-h)2+k的图象和性质
图象特点
当a>0,开口向上;当a<0,开口向下.
对称轴是x=h,
顶点坐标是(h,k).
平移规律
左右平移:括号内左加右减;
上下平移:括号外上加下减.
随堂演练
5
随堂演练
二次函数
开口方向
对称轴
顶点坐标
y=2(x+3)2+5
向上
(
1,
-2
)
向下
向下
(
3
,
7)
(
2
,
-6
)
向上
直线x=-3
直线x=1
直线x=3
直线x=2
(-3,
5
)
y=-3(x-1)2-2
y
=
4(x-3)2+7
y=-5(2-x)2-6
1.完成下列表格:
2.抛物线y=-3x2+2的图象向右平移2个单位,再向上平移1个单位,得到抛物线的解析式为______________
3.抛物线y=2x2不动,把x轴、y轴分别向上、向左平移3个单位,则在新坐标系下,此抛物线的解析式为__________________.
y=2(x-3)2-3
随堂演练
4.已知y=
(x-3)2-2的部分图象如图所示,抛物线与x轴交点的一个坐标是(1,0),则另一个交点的坐标是________.
解析:由抛物线的对称性知,对称轴为x=3,一个交点坐标是(1,0),
则另一个交点坐标是(5,0).
(5,0)
随堂演练
5.对于抛物线y=-
(x?2)2+6,下列结论:①抛物线的开口向下;②对称轴为直线x=2;③顶点坐标为(2,6);④当x>2时,y随x的增大而减小.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
D
随堂演练
6.已知点A(x1,y1)、B(x2,y2)在二次函数
y=-(x-1)2+1的图象上,若-1<x1<0,3<x2<4,则y1_____y2(填“>”、“<”或“=”).
>
解析:抛物线y=-(x-1)2+1的对称轴为直线x=1,
∵a=-1<0,
∴抛物线开口向下,
∵-1<x1<0,3<x2<4,
∴y1>y2.
随堂演练
7.抛物线
与x轴交于B,C两点,顶点为A,则△ABC的周长为(
)
A.
B.
C.12
D.
B
随堂演练
8.如图,在平面直角坐标系xOy中,抛物线y=x2向左平移1个单位,再向下平移4个单位,得到抛物线y=(x-h)2+k.所得抛物线与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
(1)求h,k的值;
解:(1)∵将抛物线y=x2向左平移1个单位,再向下平移4个单位,得到抛物线y=(x+1)2-4,
∴h=-1,k=-4;
随堂演练
(2)判断△ACD的形状,并说明理由.
(2)△ACD为直角三角形.
理由如下:由(1)得y=(x+1)2-4.
当y=0时,(x+1)2-4=0,x=-3或x=1,
∴A(-3,0),B(1,0).
当x=0时,y=(x+1)2-4=(0+1)2-4=-3,
∴C点坐标为(0,-3).
顶点坐标为D(-1,-4).
随堂演练
作出抛物线的对称轴x=-1交x轴于点E,过D作DF⊥y轴于点F,如图所示.
在Rt△AED中,AD2=22+42=20;
在Rt△AOC中,AC2=32+32=18;
在Rt△CFD中,CD2=12+12=2.
∵AC2+CD2=AD2,
∴△ACD是直角三角形.
随堂演练
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
