北师大版九年级下册2.2.2 y=ax2+c的图象与性质课件(18张PPT)
文档属性
| 名称 | 北师大版九年级下册2.2.2 y=ax2+c的图象与性质课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 18:57:00 | ||
图片预览


文档简介
第二章 二次函数
2.2 二次函数的图象与性质
第2课时 y=ax2+c的图象与性质
北师大版 九年级数学下册 教学课件
*
25
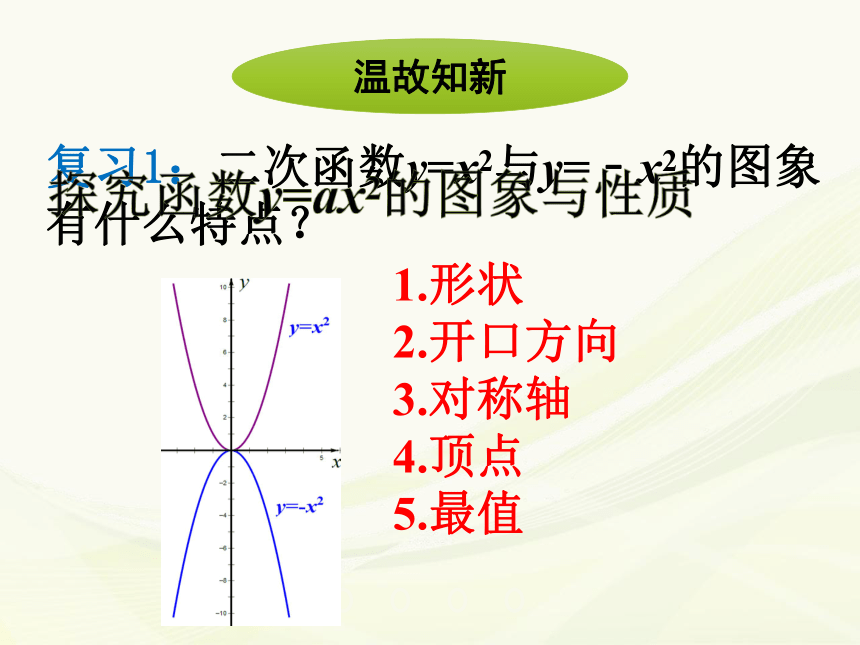
复习1:二次函数y=x2与y=﹣x2的图象有什么特点?
1.形状
2.开口方向
3.对称轴
4.顶点
5.最值
温故知新
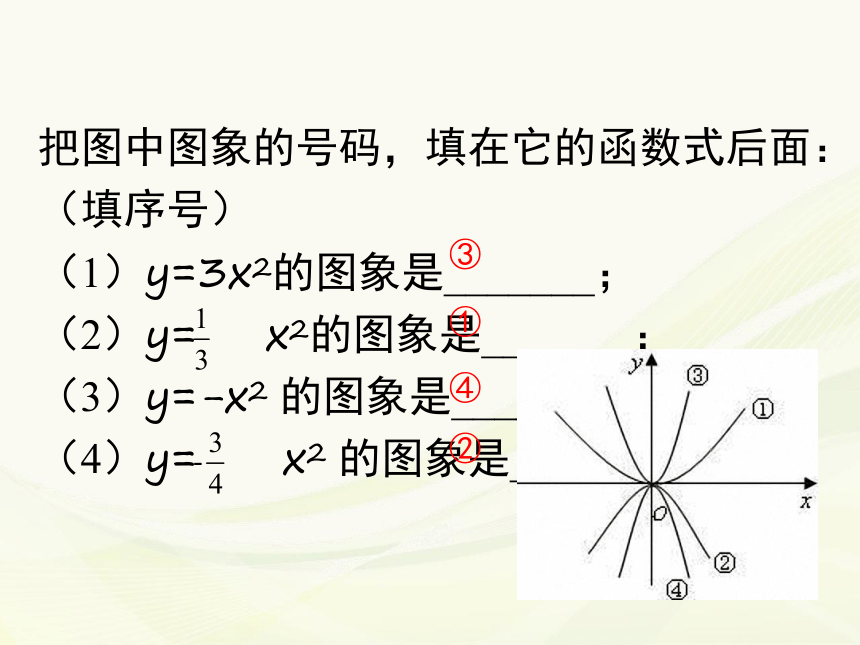
把图中图象的号码,填在它的函数式后面:(填序号)
(1)y=3x2的图象是_______;
(2)y= x2的图象是_______;
(3)y=-x2 的图象是_______;
(4)y= x2 的图象是_______.
③
①
④
②
y=ax2+1
y=x+1
y=kx-4
新课学习
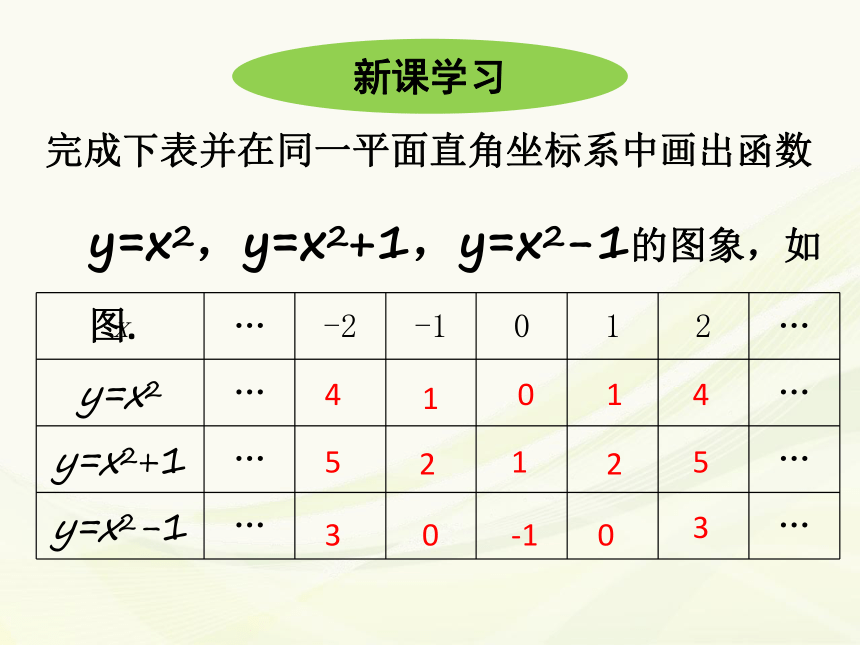
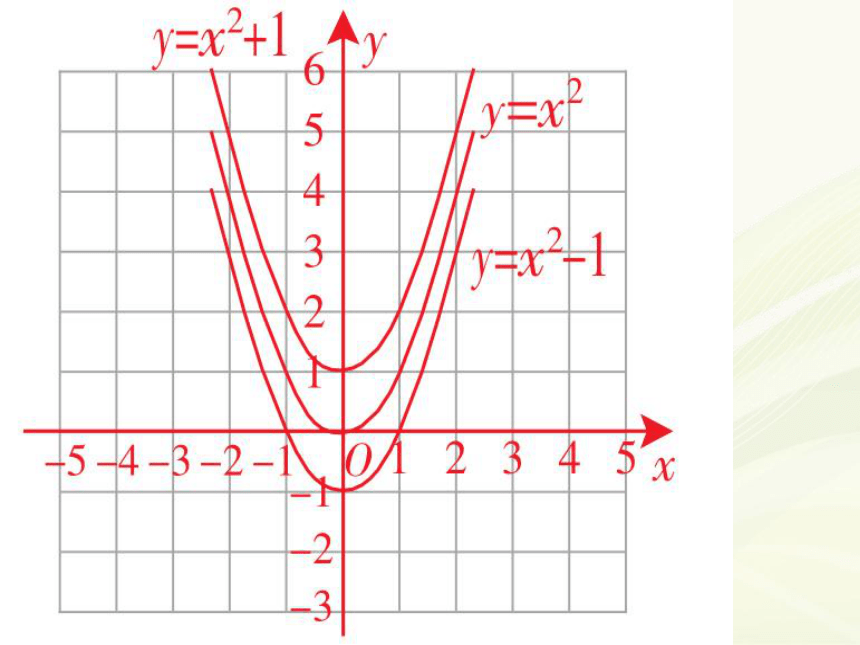
完成下表并在同一平面直角坐标系中画出函数y=x2,y=x2+1,y=x2-1的图象,如图.
x
…
-2
-1
0
1
2
…
y=x2
…
…
y=x2+1
…
…
y=x2-1
…
…
4
1
0
1
4
5
2
1
2
5
3
0
-1
0
3
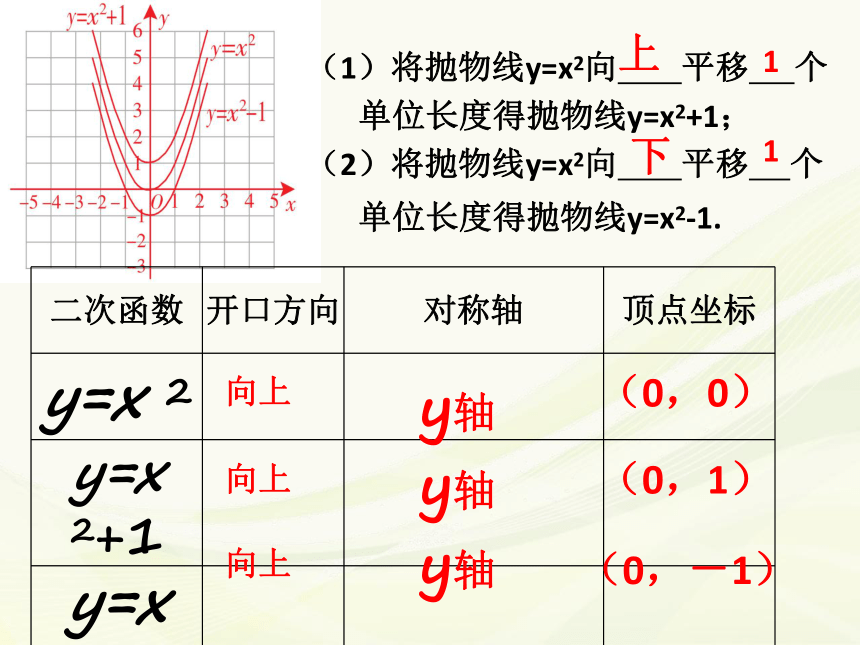
(1)将抛物线y=x2向 平移 个单位长度得抛物线y=x2+1;
(2)将抛物线y=x2向 平移 个单位长度得抛物线y=x2-1.
上
1
下
1
二次函数
开口方向
对称轴
顶点坐标
y=x 2
y=x 2+1
y=x 2-1
向上
向上
向上
y轴
y轴
y轴
(0,0)
(0,1)
(0,-1)
y=2x2-6
y=-x2 +1
y轴
(或直线x=0)
(4)抛物线y=3x2-4向下平移4个单位长度,得到的函数是__________;
函数y=3x2-4顶点坐标是_________
在x=___时,y的最____值是____
平移后的函数顶点坐标是_________
在x=___时,y的最____值是____
y=3x2-8
(0,-4)
(0,-8)
0
0
小
小
-4
-8
函数
y=ax2+c
图象
a与开口
对称轴
顶点
最值
a>0
a<0
向上
向下
y 轴或 x=0
(0,c)
x=0时ymin= c
x=0时ymax= c
小结:抛物线上下平移的规律及y=ax2+c的图象与性质:
(1)抛物线 y=ax2 向上平移 c(c>0)个单位长度,可得到的抛物线函数表达式为 .
(2)抛物线 y=ax2 向下平移 c(c>0)个单位长度,可得到的抛物线函数表达式为 .
(3)抛物线 y=ax2+c 的图象性质:
①当 a>0,开口 ;当a<0,开口 ;
②顶点坐标为 ;
③对称轴为 .
y=ax2+c
向上
向下
(0,c)
y轴(直线x=0)
y=ax2-c
y=±x2
y=2x2
y=ax2(a>0,a<0)
y=2x2±1
y=ax2+c(c>0,c<0)
一般
分类
数形结合!
a>0开口向上 a<0开口向下
|a|越大,开口越小
顶点(0,0)对称轴y轴,最值
当c>0时,向上平移|c|个单位
当c<0时,向下平移|c|个单位
(2)y=-3x2与y=3x2+3
(3)y=-2x2+2与y=-4x2+2
(1)y=3x2与y=0.3x2
巩固练习
2. 关于二次函数 y=-x2+3,下列说法中正确的是 ( )
A. 它的图象开口方向是向上
B. 当x<0时,y随x的增大而增大
C. 它的顶点坐标是(3,0)
D. 当x=0时,ymin=3
B
3. 如下图,在同一坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为 ( )
B
4. 抛物线y=2x2-6的对称轴是 ,顶点坐标是 . 当x= 时,y有最 值 .
y 轴
(0,-6)
0
小
-6
5. 若抛物线y=ax2+c与y=4x2的形状相同,
开口方向相反,且其顶点坐标是(0,2),
则该抛物线对应的函数表达式是_________.
y=-4x2+2
6. 若抛物线y=ax2+k与 x 轴没有交点,
则a,k满足的条件是________________
ak>0
二次函数 y=ax2+c的性质
y=ax2+c
a>0
a<0
开口方向
对称轴
顶点坐标
最值
增减性
要点归纳
向上
向下
y轴或直线x=0
y轴或直线x=0
(0,c)
当x=0时,y最小值=c
当x=0时,y最大值=c
当x<0时,y随x的增大而减小;x>0时,y随x的增大而增大.
当x>0时,y随x的增大而减小;x<0时,y随x的增大而增大.
(0,c)
拓展:
1.画抛物线y=ax2+c的图象有些方法?
2.抛物线y=ax2+c 中的a决定什么?c决定什么?它的对称轴是什么?顶点坐标怎样表示?
第一种方法:平移法,两步即第一步画y=ax2的图象,再向上(或向下)平移︱c ︱单位.
第二种方法:描点法,三步即列表、描点和连线.
a决定开口方向和大小;c决定顶点的纵坐标.
对称轴为y轴;顶点坐标为(0,c).
2.2 二次函数的图象与性质
第2课时 y=ax2+c的图象与性质
北师大版 九年级数学下册 教学课件
*
25
复习1:二次函数y=x2与y=﹣x2的图象有什么特点?
1.形状
2.开口方向
3.对称轴
4.顶点
5.最值
温故知新
把图中图象的号码,填在它的函数式后面:(填序号)
(1)y=3x2的图象是_______;
(2)y= x2的图象是_______;
(3)y=-x2 的图象是_______;
(4)y= x2 的图象是_______.
③
①
④
②
y=ax2+1
y=x+1
y=kx-4
新课学习
完成下表并在同一平面直角坐标系中画出函数y=x2,y=x2+1,y=x2-1的图象,如图.
x
…
-2
-1
0
1
2
…
y=x2
…
…
y=x2+1
…
…
y=x2-1
…
…
4
1
0
1
4
5
2
1
2
5
3
0
-1
0
3
(1)将抛物线y=x2向 平移 个单位长度得抛物线y=x2+1;
(2)将抛物线y=x2向 平移 个单位长度得抛物线y=x2-1.
上
1
下
1
二次函数
开口方向
对称轴
顶点坐标
y=x 2
y=x 2+1
y=x 2-1
向上
向上
向上
y轴
y轴
y轴
(0,0)
(0,1)
(0,-1)
y=2x2-6
y=-x2 +1
y轴
(或直线x=0)
(4)抛物线y=3x2-4向下平移4个单位长度,得到的函数是__________;
函数y=3x2-4顶点坐标是_________
在x=___时,y的最____值是____
平移后的函数顶点坐标是_________
在x=___时,y的最____值是____
y=3x2-8
(0,-4)
(0,-8)
0
0
小
小
-4
-8
函数
y=ax2+c
图象
a与开口
对称轴
顶点
最值
a>0
a<0
向上
向下
y 轴或 x=0
(0,c)
x=0时ymin= c
x=0时ymax= c
小结:抛物线上下平移的规律及y=ax2+c的图象与性质:
(1)抛物线 y=ax2 向上平移 c(c>0)个单位长度,可得到的抛物线函数表达式为 .
(2)抛物线 y=ax2 向下平移 c(c>0)个单位长度,可得到的抛物线函数表达式为 .
(3)抛物线 y=ax2+c 的图象性质:
①当 a>0,开口 ;当a<0,开口 ;
②顶点坐标为 ;
③对称轴为 .
y=ax2+c
向上
向下
(0,c)
y轴(直线x=0)
y=ax2-c
y=±x2
y=2x2
y=ax2(a>0,a<0)
y=2x2±1
y=ax2+c(c>0,c<0)
一般
分类
数形结合!
a>0开口向上 a<0开口向下
|a|越大,开口越小
顶点(0,0)对称轴y轴,最值
当c>0时,向上平移|c|个单位
当c<0时,向下平移|c|个单位
(2)y=-3x2与y=3x2+3
(3)y=-2x2+2与y=-4x2+2
(1)y=3x2与y=0.3x2
巩固练习
2. 关于二次函数 y=-x2+3,下列说法中正确的是 ( )
A. 它的图象开口方向是向上
B. 当x<0时,y随x的增大而增大
C. 它的顶点坐标是(3,0)
D. 当x=0时,ymin=3
B
3. 如下图,在同一坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为 ( )
B
4. 抛物线y=2x2-6的对称轴是 ,顶点坐标是 . 当x= 时,y有最 值 .
y 轴
(0,-6)
0
小
-6
5. 若抛物线y=ax2+c与y=4x2的形状相同,
开口方向相反,且其顶点坐标是(0,2),
则该抛物线对应的函数表达式是_________.
y=-4x2+2
6. 若抛物线y=ax2+k与 x 轴没有交点,
则a,k满足的条件是________________
ak>0
二次函数 y=ax2+c的性质
y=ax2+c
a>0
a<0
开口方向
对称轴
顶点坐标
最值
增减性
要点归纳
向上
向下
y轴或直线x=0
y轴或直线x=0
(0,c)
当x=0时,y最小值=c
当x=0时,y最大值=c
当x<0时,y随x的增大而减小;x>0时,y随x的增大而增大.
当x>0时,y随x的增大而减小;x<0时,y随x的增大而增大.
(0,c)
拓展:
1.画抛物线y=ax2+c的图象有些方法?
2.抛物线y=ax2+c 中的a决定什么?c决定什么?它的对称轴是什么?顶点坐标怎样表示?
第一种方法:平移法,两步即第一步画y=ax2的图象,再向上(或向下)平移︱c ︱单位.
第二种方法:描点法,三步即列表、描点和连线.
a决定开口方向和大小;c决定顶点的纵坐标.
对称轴为y轴;顶点坐标为(0,c).
