北师大版九年级数学下册:2.2.2二次函数的图象与性质(2)(11张PPT)
文档属性
| 名称 | 北师大版九年级数学下册:2.2.2二次函数的图象与性质(2)(11张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 424.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 22:22:53 | ||
图片预览



文档简介
2 二次函数的图象与性质
第二章 二次函数
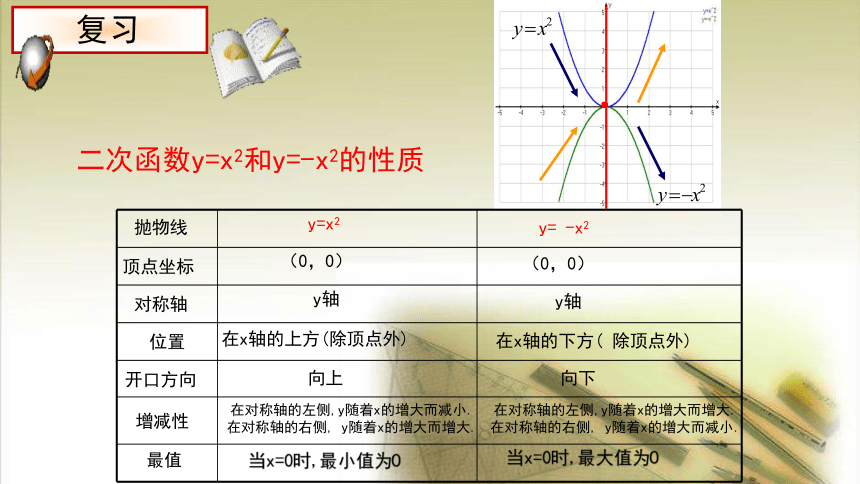
二次函数y=x2和y=-x2的性质
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=x2
y= -x2
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0
当x=0时,最大值为0
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
复习
你会用描点法画二次函数y=x2、y=2x2、y=3x2的图象吗?
想一想
解:1、列表
x
y=x2
y=2x2
y=3x2
-3
0
-1
-2
1
2
3
9
4
1
0
1
4
9
18
8
2
0
2
8
18
27
12
3
0
3
12
27
…
…
…
…
…
…
…
…
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
12
14
16
18
20
22
24
26
28
-4
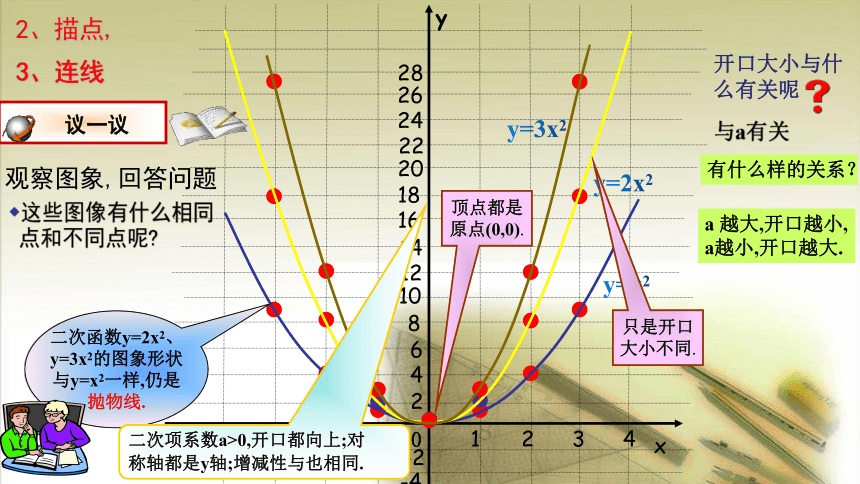
2、描点,
3、连线
y=x2
y=2x2
y=3x2
二次函数y=2x2、
y=3x2的图象形状
与y=x2一样,仍是
抛物线.
议一议
二次项系数a>0,开口都向上;对
称轴都是y轴;增减性与也相同.
顶点都是
原点(0,0).
只是开口
大小不同.
观察图象,回答问题
这些图像有什么相同
点和不同点呢?
开口大小与什么有关呢
与a有关
a 越大,开口越小,
a越小,开口越大.
有什么样的关系?
想一想
在同一坐标系中作二次函数y=-x2、y=-2x2和
y=-3x2的图象,会是什么样?
解:1、列表
x
y=-x2
y=-2x2
y=-3x2
-3
0
-1
-2
1
2
3
-9
-4
-1
0
-1
-4
-9
-18
-8
-2
0
-2
-8
-18
-27
-12
-3
0
-3
-12
-27
…
…
…
…
…
…
…
…
x
y
0
-4
-3
-2
-1
1
2
3
4
-20
-22
-24
-26
-28
-18
-16
-14
-12
-10
-8
-6
-4
-2
-30
y=-x2
y=-2x2
y=-3x2
二次函数y=-2x2、
y=-3x2的图象形状
与y=-x2一样,仍是
抛物线.
二次项系数a<0,开口都向下;对
称轴都是y轴;增减性与也相同.
顶点都是
原点(0,0).
只是开口
大小不同.
开口大小与什么有关呢
与a有关
有什么样的关系?
a 越小,开口越小,
a越大,开口越大.
二次函数y=ax2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
开口大小
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2 (a>0)
y= ax2 (a<0)
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
越小,开口越大.
越大,开口越小.
总结:
例题讲解解
例1 把图中图像的序号填在与它相应的函数表达式后面.
(1) 的图像是 ;
(2) 的图像是 ;
(3) 的图像是 ;
(4) 的图像是 .
③
②
①
④
例题讲解解
例2 . 二次函数 , , 的共有性质是( )。
A.图像开口都向上
B.图像都有最低点
C.图像都关于y轴对称
D.y随x的增大而减小
C
例题讲解解
B
例3 . 若抛物线 的图像开口向下,则 的取值范围是( ).
A.
B.
C.
D.
下课了!
再见
第二章 二次函数
二次函数y=x2和y=-x2的性质
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=x2
y= -x2
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0
当x=0时,最大值为0
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
复习
你会用描点法画二次函数y=x2、y=2x2、y=3x2的图象吗?
想一想
解:1、列表
x
y=x2
y=2x2
y=3x2
-3
0
-1
-2
1
2
3
9
4
1
0
1
4
9
18
8
2
0
2
8
18
27
12
3
0
3
12
27
…
…
…
…
…
…
…
…
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
12
14
16
18
20
22
24
26
28
-4
2、描点,
3、连线
y=x2
y=2x2
y=3x2
二次函数y=2x2、
y=3x2的图象形状
与y=x2一样,仍是
抛物线.
议一议
二次项系数a>0,开口都向上;对
称轴都是y轴;增减性与也相同.
顶点都是
原点(0,0).
只是开口
大小不同.
观察图象,回答问题
这些图像有什么相同
点和不同点呢?
开口大小与什么有关呢
与a有关
a 越大,开口越小,
a越小,开口越大.
有什么样的关系?
想一想
在同一坐标系中作二次函数y=-x2、y=-2x2和
y=-3x2的图象,会是什么样?
解:1、列表
x
y=-x2
y=-2x2
y=-3x2
-3
0
-1
-2
1
2
3
-9
-4
-1
0
-1
-4
-9
-18
-8
-2
0
-2
-8
-18
-27
-12
-3
0
-3
-12
-27
…
…
…
…
…
…
…
…
x
y
0
-4
-3
-2
-1
1
2
3
4
-20
-22
-24
-26
-28
-18
-16
-14
-12
-10
-8
-6
-4
-2
-30
y=-x2
y=-2x2
y=-3x2
二次函数y=-2x2、
y=-3x2的图象形状
与y=-x2一样,仍是
抛物线.
二次项系数a<0,开口都向下;对
称轴都是y轴;增减性与也相同.
顶点都是
原点(0,0).
只是开口
大小不同.
开口大小与什么有关呢
与a有关
有什么样的关系?
a 越小,开口越小,
a越大,开口越大.
二次函数y=ax2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
开口大小
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2 (a>0)
y= ax2 (a<0)
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
越小,开口越大.
越大,开口越小.
总结:
例题讲解解
例1 把图中图像的序号填在与它相应的函数表达式后面.
(1) 的图像是 ;
(2) 的图像是 ;
(3) 的图像是 ;
(4) 的图像是 .
③
②
①
④
例题讲解解
例2 . 二次函数 , , 的共有性质是( )。
A.图像开口都向上
B.图像都有最低点
C.图像都关于y轴对称
D.y随x的增大而减小
C
例题讲解解
B
例3 . 若抛物线 的图像开口向下,则 的取值范围是( ).
A.
B.
C.
D.
下课了!
再见
