北师大版数学四年级下册 2.3 探索与发现:三角形内角和 课件(16张ppt)
文档属性
| 名称 | 北师大版数学四年级下册 2.3 探索与发现:三角形内角和 课件(16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 07:11:19 | ||
图片预览





文档简介
二
认识三角形和四边形
第3课时 探索与发现:三角形
内角和
经历测量、拼接、折叠的过程,探索并发现三角形内角和的规律,渗透归纳思想。
1.
2.
能运用三角形内角和解决一些简单的实际问题,培养应用数学的意识。
教学目标
小组活动:每人准备一个三角形,量一量,填一填。
小组活动记录表 第 组
小组成员姓名
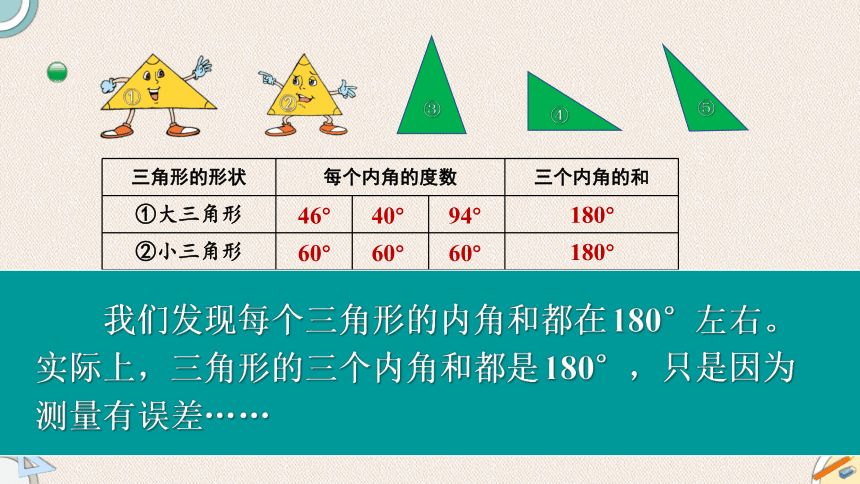
三角形的形状
每个内角的度数
三个内角的和
三角形的形状
每个内角的度数
三个内角的和
①大三角形
②小三角形
③锐角三角形
④直角三角形
⑤钝角三角形
③
④
⑤
①
②
小组交流发现了什么。
46°
40°
94°
180°
60°
60°
60°
180°
69°
70°
40°
179°
90°
30°
60°
180°
120°
41°
20°
181°
我们发现每个三角形的内角和都在180°左右。实际上,三角形的三个内角和都是180°,只是因为测量有误差……
方法一:把三角形的三个角撕下来,拼在一起,如图。
∠1,∠2,∠3正好拼成一个平角,说明三角形的内角和是180°。
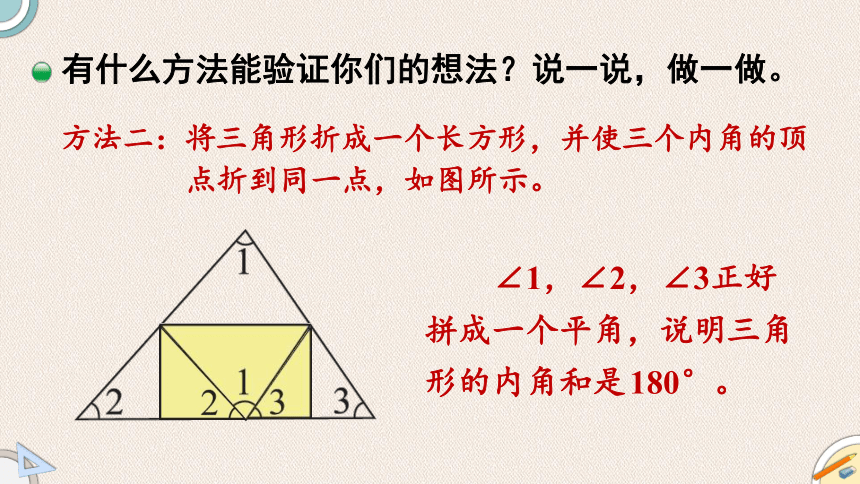
有什么方法能验证你们的想法?说一说,做一做。
方法二:将三角形折成一个长方形,并使三个内角的顶
点折到同一点,如图所示。
∠1,∠2,∠3正好拼成一个平角,说明三角形的内角和是180°。
有什么方法能验证你们的想法?说一说,做一做。
有什么方法能验证你们的想法?说一说,做一做。
综上可以得出结论:三角形的内角和等于180°。也就是说,三角形的内角和与三角形的大小、形状无关,三角形的内角和永远是180°。
60°
40°
80°
180?60?40=80°
锐角三角形
猜一猜,可能是什么三角形?
锐角三角形、直角三角形和钝角三角形都有可能。
猜一猜,可能是什么三角形?
1. 如图,用两把完全相同的三角尺分别拼出一个四边
形和一个三角形。
四边形内角和:90°+ 90°+90°+90°=360°
三角形内角和:90°+ 45°+ 45°=180°
所以,它们的内角和分别是360°和180°。
(1)想一想,它们的内角和分别
是多少?与同伴交流你是怎
么想的。
(2)量一量,算算它们的内角和。
2. 用一张长方形纸剪一剪,再填一填。
长方
三角
三角
三角
180
360
180
180
3. 它们说得对吗?
4. 填出下面各角的度数。
77°
55°
115°
1. 三角形内角和等于180°。
2. 根据“三角形内角和等于180°” ,当已知三角
形中两个内角的度数时,可以求出第三个内角的
度数,并可以由此判断三角形的形状。
认识三角形和四边形
第3课时 探索与发现:三角形
内角和
经历测量、拼接、折叠的过程,探索并发现三角形内角和的规律,渗透归纳思想。
1.
2.
能运用三角形内角和解决一些简单的实际问题,培养应用数学的意识。
教学目标
小组活动:每人准备一个三角形,量一量,填一填。
小组活动记录表 第 组
小组成员姓名
三角形的形状
每个内角的度数
三个内角的和
三角形的形状
每个内角的度数
三个内角的和
①大三角形
②小三角形
③锐角三角形
④直角三角形
⑤钝角三角形
③
④
⑤
①
②
小组交流发现了什么。
46°
40°
94°
180°
60°
60°
60°
180°
69°
70°
40°
179°
90°
30°
60°
180°
120°
41°
20°
181°
我们发现每个三角形的内角和都在180°左右。实际上,三角形的三个内角和都是180°,只是因为测量有误差……
方法一:把三角形的三个角撕下来,拼在一起,如图。
∠1,∠2,∠3正好拼成一个平角,说明三角形的内角和是180°。
有什么方法能验证你们的想法?说一说,做一做。
方法二:将三角形折成一个长方形,并使三个内角的顶
点折到同一点,如图所示。
∠1,∠2,∠3正好拼成一个平角,说明三角形的内角和是180°。
有什么方法能验证你们的想法?说一说,做一做。
有什么方法能验证你们的想法?说一说,做一做。
综上可以得出结论:三角形的内角和等于180°。也就是说,三角形的内角和与三角形的大小、形状无关,三角形的内角和永远是180°。
60°
40°
80°
180?60?40=80°
锐角三角形
猜一猜,可能是什么三角形?
锐角三角形、直角三角形和钝角三角形都有可能。
猜一猜,可能是什么三角形?
1. 如图,用两把完全相同的三角尺分别拼出一个四边
形和一个三角形。
四边形内角和:90°+ 90°+90°+90°=360°
三角形内角和:90°+ 45°+ 45°=180°
所以,它们的内角和分别是360°和180°。
(1)想一想,它们的内角和分别
是多少?与同伴交流你是怎
么想的。
(2)量一量,算算它们的内角和。
2. 用一张长方形纸剪一剪,再填一填。
长方
三角
三角
三角
180
360
180
180
3. 它们说得对吗?
4. 填出下面各角的度数。
77°
55°
115°
1. 三角形内角和等于180°。
2. 根据“三角形内角和等于180°” ,当已知三角
形中两个内角的度数时,可以求出第三个内角的
度数,并可以由此判断三角形的形状。
