北师大版九年级数学下册 2.4二次函数的应用 同步测试(word版 含答案)
文档属性
| 名称 | 北师大版九年级数学下册 2.4二次函数的应用 同步测试(word版 含答案) | 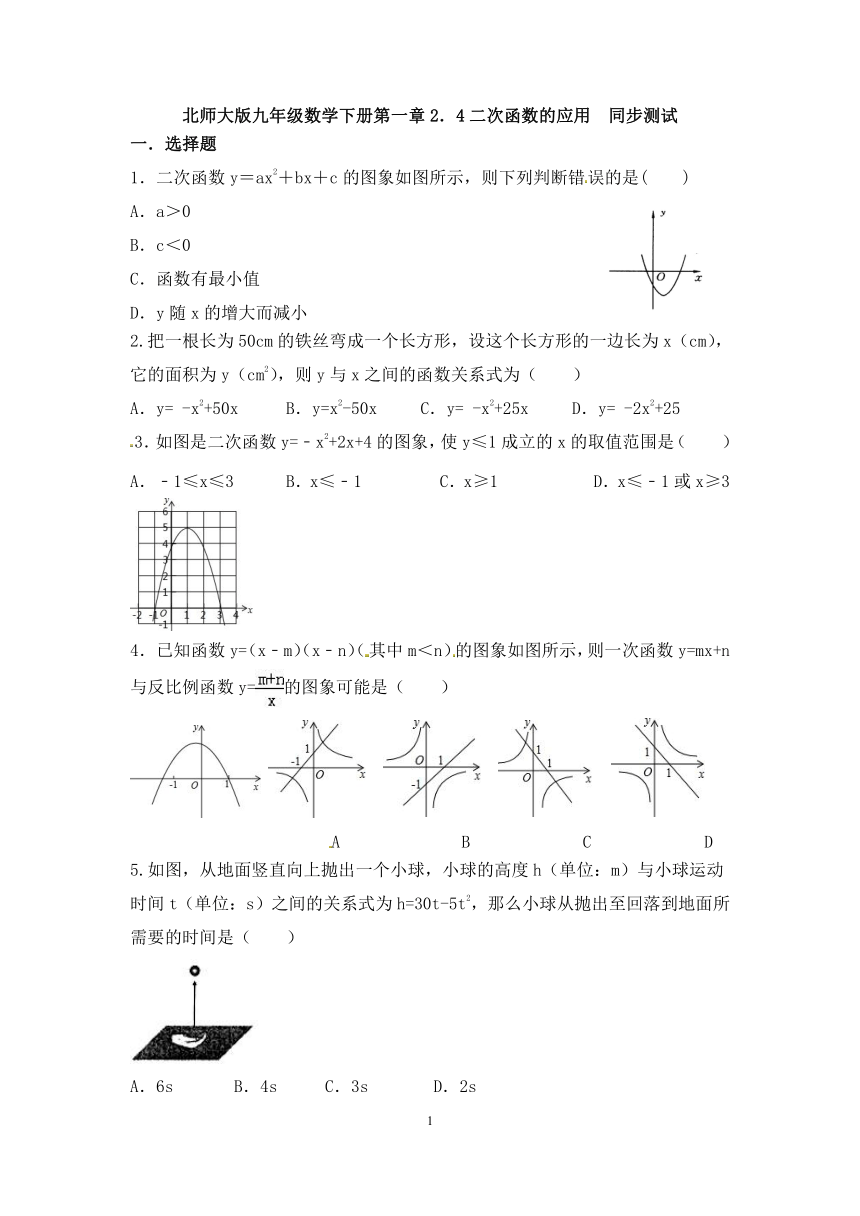 | |
| 格式 | zip | ||
| 文件大小 | 238.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 08:50:03 | ||
图片预览




文档简介
北师大版九年级数学下册第一章2.4二次函数的应用
同步测试
一.选择题
1.二次函数y=ax2+bx+c的图象如图所示,则下列判断错误的是(
)
a>0
c<0
函数有最小值
y随x的增大而减小
2.把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )
A.y=
-x2+50x
B.y=x2-50x
C.y=
-x2+25x
D.y=
-2x2+25
3.如图是二次函数y=﹣x2+2x+4的图象,使y≤1成立的x的取值范围是( )
﹣1≤x≤3
B.x≤﹣1
C.x≥1
D.x≤﹣1或x≥3
已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A
B
C
D
5.如图,从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为h=30t-5t2,那么小球从抛出至回落到地面所需要的时间是( )
A.6s
B.4s
C.3s
D.2s
6.某商品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查反映;如调整价格,每涨价1元,每星期要少卖出10件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=300﹣10x
B.y=300(60﹣40﹣x)
C.y=(300+10x)(60﹣40﹣x)
D.y=(300﹣10x)(60﹣40+x)
7.如图,隧道的截面是抛物线,可以用y=
表示,该隧道内设双行道,限高为3m,那么每条行道宽是( )
A.不大于4m
B.恰好4m
C.不小于4m
D.大于4m,小于8m
8.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒
B.第10秒
C.第12秒
D.第15秒
9.用长为8m的铝合金条制成如图所示的矩形窗框,则这个窗户的最大采光面积是( )
A.m2
B.m2
C.3m2
D.m2
10.如图所示,桥拱是抛物线形,其函数的表达式为y=
-x2,当水位线在AB位置时,水面宽12m,这时水面离桥顶的高度为( )
A.3m
B.
m
C.
m
D.9
m
11.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB间,按相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为( )
A.0.4米
B.0.16米
C.0.2米
D.0.24米
12.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是80m
②小球抛出后至3秒,速度越来越慢
③小球抛出6秒时速度为0
④小球的高度h=30m时,t=1.8s
其中正确的是( )
A.①②
B.①④
C.②③④
D.①②③
二.填空题
抛物线y=x2+bx+c与x轴的正半轴交于A,B两点,与y轴交于C点,且线段AB的长为1,△ABC的面积为l,则b的值是
.
14.某商店将进货价为70元/个的商品按零售价100元/个出售时,每天能卖出20个,若零售价在一定范围内每降价1元,其日销售量就增加1个,为了获得最大利润,则应降价
元.
15.一名男生参加抛实心球测试,已知球的高度y(m)与水平距离x(m)之间的关系是,则这名男生抛实心球的成绩是
m.
16.学校准备建一个矩形花圃,其中一边靠墙,另外三边用周长为30米的篱笆围成,已知墙长为18米,设花圃垂直于墙的一边长为x米,花圃的面积为y平方米,写出y与x的函数关系式,并写出自变量x的取值范围
.
17.某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件,商品进价为每件40元,若设涨价x(x>0)元,总利润为y元,则y与x的函数关系式为
.
18.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为____________
19.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30﹣x)件.若使利润最大,每件的售价应为 元.
20.如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P.Q分别从A.B同时出发,那么经过____秒,四边形APQC的面积最小.
三.解答题
21.每年六七月份我市荔枝大量上市,今年某水果商以5元/千克的价格购进一批荔枝进行销售,运输过程中质量损耗5%,运输费用是0.7元/千克,假设不计其他费用.
(1)水果商要把荔枝售价至少定为多少才不会亏本?
(2)在销售过程中,水果商发现每天荔枝的销售量m(千克)与销售单价x(元/千克)之间满足关系:m=
-10x+120,那么当销售单价定为多少时,每天获得的利润w最大?
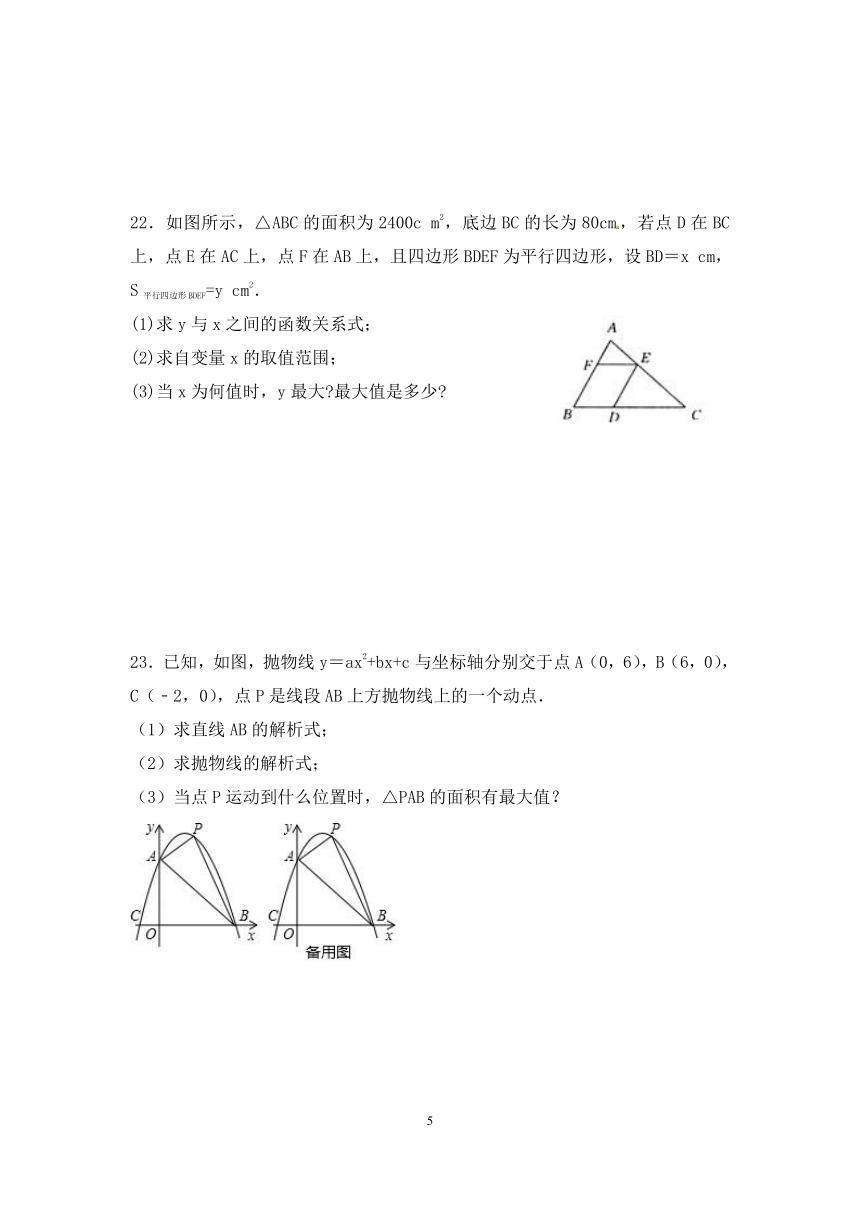
22.如图所示,△ABC的面积为2400c
m2,底边BC的长为80cm,若点D在BC上,点E在AC上,点F在AB上,且四边形BDEF为平行四边形,设BD=x
cm,S平行四边形BDEF=y
cm2.
(1)求y与x之间的函数关系式;
(2)求自变量x的取值范围;
(3)当x为何值时,y最大?最大值是多少?
23.已知,如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求直线AB的解析式;
(2)求抛物线的解析式;
(3)当点P运动到什么位置时,△PAB的面积有最大值?
24.二次函数图象的顶点在原点O,经过点A(1,),点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
25.如图,在平面直角坐标系中,直线y=kx+1与x轴交于点A,与y轴交于点C,过点C的抛物线y=ax2﹣(6a﹣2)x+b与直线AC交于另一点B(4,3).
(1)求抛物线的表达式;
(2)已知x轴上一动点Q(m,0),连接BQ,若△ABQ与△AOC相似,求出m的值.
26.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C(0,﹣3),A点的坐标为(﹣1,0).
(1)求二次函数的解析式;
(2)若点P是抛物线在第四象限上的一个动点,当四边形ABPC的面积最大时,求点P的坐标,并求出四边形ABPC的最大面积;
(3)若Q为抛物线对称轴上一动点,当Q在什么位置时QA+QC最小,求出Q点的坐标,并求出此时△QAC的周长.
答案提示
1.D.
2.C.3.D.4.C.5.A.6.D.7.A.8.B.9.B.10.D.
11.解:如图,以C坐标系的原点,OC所在直线为y轴建立坐标系,
设抛物线解析式为y=ax2,
由题知,图象过B(0.6,0.36),
代入得:0.36=0.36a
∴a=1,即y=x2.
∵F点横坐标为-0.4,
∴当x=
-0.4时,y=0.16,
∴EF=0.36-0.16=0.2米
故选C.
12.解:①由图象可知,小球在空中达到的最大高度为40m,则小球在下落到地面又走了40m,共经过80m,故①正确;
②小球抛出3秒后,速度越来越快;故②正确;
③小球抛出3秒时达到最高点,即速度为0,小球抛出6秒时速度不为0,故③错误;
④设函数解析式为h=a(t﹣3)2+40,将(0,0)代入得:
0=a(0﹣3)2+40,
解得a=﹣,
∴函数解析式为h=﹣(t﹣3)2+40,
∴当h=30m时,30=﹣(t﹣3)2+40,
解得:t=4.5或t=1.5,
∴小球的高度h=30m时,t=1.5s或4.5s,故④错误;
综上,正确的有①②,
故选:A.
13.-3.
14.5.
15.
10.
16.y=﹣2x2+30x(6≤x<15).
17.y=﹣10x2+100x+6000.
18.0.5米.
19.25.
20.解:设P.Q同时出发后经过的时间为t秒,四边形APQC的面积为S平方毫米,
则有:S=S△ABC-S△PBQ
=
=4t2-24t+144
=4(t-3)2+108.
∵4>0
∴当t=3s时,S取得最小值.
21.解:(1)设购进荔枝a千克,荔枝售价定为b元/千克时,水果商才不会亏本,由题意得
ba(1-5%)≥(5+0.7)a,
∵a>0,
∴95%b≥5.7
∴b≥6
所以,水果商要把荔枝售价至少定为6元/千克才不会亏本.
(2)由(1)可知,每千克荔枝的平均成本为6元,由题意得
w=(x-6)m
=(x-6)(-10x+120)
=
-10(x-9)2+90,
∵a=
-10<0
∴w有最大值
∴当x=9时,w有最大值.
所以,当销售单价定为9元/千克时,每天可获利润w最大.
22.解:(1)设A到BC的距离为d
cm,E到BC的距离为h
cm,则y=S平行四边形BDEF=xh.∵S△ABC=BC·d,∴2400=×80d,∴d=60.∵ED∥AB,∴△EDC∽△ABC,∴,即,∴h=,∴y=x=-x2+60x.(2)自变量x的取值范围是0<x<80.
(3)∵a=-<0,-=40,0<40<80,∴当x=40时,y最大值=1200.
23.解:(1)设直线AB的解析式为y=kx+b(k≠0),
将点A(0,6),B(6,0)代入y=kx+b(k≠0),得,
∴,
则直线AB的解析式为y=﹣x+6;
(2)∵抛物线过点B(6,0),C(﹣2,0),
∴设抛物线的解析式为y=a(x﹣6)(x+2)(a≠0),
将点A(0,6)代入y=a(x﹣6)(x+2),得﹣12a=6,
解得a=﹣,
∴抛物线的解析式为y=﹣(x﹣6)(x+2)=﹣x2+2x+6;
(3)如图,
过点P作PN∥y轴,交AB于N,
设P点坐标为(t,﹣t2+2t+6)(0<t<6),
则N(t,﹣t+6),
∴PN=yP﹣yN=﹣t2+2t+6﹣(﹣t+6)=﹣t2+2t+6+t﹣6=﹣t2+3t.
∴S△PAB=S△PAN+S△PBN
=PN?|xP﹣xA|+PN?|xB﹣xP|
=PN?(xB﹣xA)=×(﹣t2+3t)×6
=﹣(t﹣3)2+,
∴当t=3,即点P位于(3,)时,△PAB的面积有最大值.
24.解:(1)∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为y=ax2,
将点A(1,)代入y=ax2得:a=,
∴二次函数的解析式为y=x2;
(2)证明:∵点P在抛物线y=x2上,
∴可设点P的坐标为(x,x2),
如图,过点P作PB⊥y轴于点B,则BF=x2﹣1,PB=x,
∴Rt△BPF中,
PF==x2+1,
∵PM⊥直线y=﹣1,
∴PM=x2+1,
∴PF=PM,
∴∠PFM=∠PMF,
又∵PM∥x轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP;
(3)当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,
∴x2+1=4,
解得:x=±2,
∴x2=×12=3,
∴满足条件的点P的坐标为(2,3)或(﹣2,3).
25.解:(1)点C的坐标为(0,1),b=1,
将点B坐标代入代入一次函数表达式得:3=4k+1,解得:k=,
则一次函数表达式为:y=x+1,则点A坐标为(﹣2,0),
把点C.B坐标代入二次函数表达式得:3=a×42﹣4(6a﹣2)+1,解得:a=,
则二次函数表达式为:y=x2﹣x+1;
(2)①如下图,当∠AQB=90°时,
△ABQ与△AOC相似,m=4,
②当∠ABQ=90°时,△ABQ与△AOC相似,
AB==3,cos∠BAO==,
则AQ==,
则m=﹣2=,
即:m的值为4或.
26.解:(1)∵A(﹣1,0),C(0,﹣3)在y=x2+bx+c上,
则,解得,
∴二次函数的解析式为y=x2﹣2x﹣3;
(2)在y=x2﹣2x﹣3中,令y=0可得0=x2﹣2x﹣3,解得x=3或x=﹣1,
∴B(3,0),且C(0,﹣3),
∴经过B.C两点的直线为y=x﹣3,
设点P的坐标为(x,x2﹣2x﹣3),如图,过点P作PD⊥x轴,垂足为D,与直线BC交于点E,则E(x,x﹣3),
∵S四边形ABPC=S△ABC+S△BCP=×4×3+(3x﹣x2)×3=﹣x2+x+6=﹣(x﹣)2+,
∴当x=时,四边形ABPC的面积最大,此时P点坐标为(,﹣),
∴四边形ABPC的最大面积为;
(3)点A关于函数对称轴的对称点为点B,连接BC交函数对称轴于点Q,连接AQ,则此时△QAC的周长最小,
理由:△QAC的周长=AC+AQ+QC=AB+AQ+QC=BC+CQ为最小,
由点B.C的坐标得,直线BC的表达式为y=x﹣3,
当x=1时,y=x﹣3=﹣2,即点Q(1,﹣2),
则△QAC的周长最小值=BC+AC=3+=3+.
同步测试
一.选择题
1.二次函数y=ax2+bx+c的图象如图所示,则下列判断错误的是(
)
a>0
c<0
函数有最小值
y随x的增大而减小
2.把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )
A.y=
-x2+50x
B.y=x2-50x
C.y=
-x2+25x
D.y=
-2x2+25
3.如图是二次函数y=﹣x2+2x+4的图象,使y≤1成立的x的取值范围是( )
﹣1≤x≤3
B.x≤﹣1
C.x≥1
D.x≤﹣1或x≥3
已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A
B
C
D
5.如图,从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为h=30t-5t2,那么小球从抛出至回落到地面所需要的时间是( )
A.6s
B.4s
C.3s
D.2s
6.某商品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查反映;如调整价格,每涨价1元,每星期要少卖出10件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=300﹣10x
B.y=300(60﹣40﹣x)
C.y=(300+10x)(60﹣40﹣x)
D.y=(300﹣10x)(60﹣40+x)
7.如图,隧道的截面是抛物线,可以用y=
表示,该隧道内设双行道,限高为3m,那么每条行道宽是( )
A.不大于4m
B.恰好4m
C.不小于4m
D.大于4m,小于8m
8.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒
B.第10秒
C.第12秒
D.第15秒
9.用长为8m的铝合金条制成如图所示的矩形窗框,则这个窗户的最大采光面积是( )
A.m2
B.m2
C.3m2
D.m2
10.如图所示,桥拱是抛物线形,其函数的表达式为y=
-x2,当水位线在AB位置时,水面宽12m,这时水面离桥顶的高度为( )
A.3m
B.
m
C.
m
D.9
m
11.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB间,按相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为( )
A.0.4米
B.0.16米
C.0.2米
D.0.24米
12.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是80m
②小球抛出后至3秒,速度越来越慢
③小球抛出6秒时速度为0
④小球的高度h=30m时,t=1.8s
其中正确的是( )
A.①②
B.①④
C.②③④
D.①②③
二.填空题
抛物线y=x2+bx+c与x轴的正半轴交于A,B两点,与y轴交于C点,且线段AB的长为1,△ABC的面积为l,则b的值是
.
14.某商店将进货价为70元/个的商品按零售价100元/个出售时,每天能卖出20个,若零售价在一定范围内每降价1元,其日销售量就增加1个,为了获得最大利润,则应降价
元.
15.一名男生参加抛实心球测试,已知球的高度y(m)与水平距离x(m)之间的关系是,则这名男生抛实心球的成绩是
m.
16.学校准备建一个矩形花圃,其中一边靠墙,另外三边用周长为30米的篱笆围成,已知墙长为18米,设花圃垂直于墙的一边长为x米,花圃的面积为y平方米,写出y与x的函数关系式,并写出自变量x的取值范围
.
17.某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件,商品进价为每件40元,若设涨价x(x>0)元,总利润为y元,则y与x的函数关系式为
.
18.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为____________
19.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30﹣x)件.若使利润最大,每件的售价应为 元.
20.如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P.Q分别从A.B同时出发,那么经过____秒,四边形APQC的面积最小.
三.解答题
21.每年六七月份我市荔枝大量上市,今年某水果商以5元/千克的价格购进一批荔枝进行销售,运输过程中质量损耗5%,运输费用是0.7元/千克,假设不计其他费用.
(1)水果商要把荔枝售价至少定为多少才不会亏本?
(2)在销售过程中,水果商发现每天荔枝的销售量m(千克)与销售单价x(元/千克)之间满足关系:m=
-10x+120,那么当销售单价定为多少时,每天获得的利润w最大?
22.如图所示,△ABC的面积为2400c
m2,底边BC的长为80cm,若点D在BC上,点E在AC上,点F在AB上,且四边形BDEF为平行四边形,设BD=x
cm,S平行四边形BDEF=y
cm2.
(1)求y与x之间的函数关系式;
(2)求自变量x的取值范围;
(3)当x为何值时,y最大?最大值是多少?
23.已知,如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求直线AB的解析式;
(2)求抛物线的解析式;
(3)当点P运动到什么位置时,△PAB的面积有最大值?
24.二次函数图象的顶点在原点O,经过点A(1,),点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
25.如图,在平面直角坐标系中,直线y=kx+1与x轴交于点A,与y轴交于点C,过点C的抛物线y=ax2﹣(6a﹣2)x+b与直线AC交于另一点B(4,3).
(1)求抛物线的表达式;
(2)已知x轴上一动点Q(m,0),连接BQ,若△ABQ与△AOC相似,求出m的值.
26.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C(0,﹣3),A点的坐标为(﹣1,0).
(1)求二次函数的解析式;
(2)若点P是抛物线在第四象限上的一个动点,当四边形ABPC的面积最大时,求点P的坐标,并求出四边形ABPC的最大面积;
(3)若Q为抛物线对称轴上一动点,当Q在什么位置时QA+QC最小,求出Q点的坐标,并求出此时△QAC的周长.
答案提示
1.D.
2.C.3.D.4.C.5.A.6.D.7.A.8.B.9.B.10.D.
11.解:如图,以C坐标系的原点,OC所在直线为y轴建立坐标系,
设抛物线解析式为y=ax2,
由题知,图象过B(0.6,0.36),
代入得:0.36=0.36a
∴a=1,即y=x2.
∵F点横坐标为-0.4,
∴当x=
-0.4时,y=0.16,
∴EF=0.36-0.16=0.2米
故选C.
12.解:①由图象可知,小球在空中达到的最大高度为40m,则小球在下落到地面又走了40m,共经过80m,故①正确;
②小球抛出3秒后,速度越来越快;故②正确;
③小球抛出3秒时达到最高点,即速度为0,小球抛出6秒时速度不为0,故③错误;
④设函数解析式为h=a(t﹣3)2+40,将(0,0)代入得:
0=a(0﹣3)2+40,
解得a=﹣,
∴函数解析式为h=﹣(t﹣3)2+40,
∴当h=30m时,30=﹣(t﹣3)2+40,
解得:t=4.5或t=1.5,
∴小球的高度h=30m时,t=1.5s或4.5s,故④错误;
综上,正确的有①②,
故选:A.
13.-3.
14.5.
15.
10.
16.y=﹣2x2+30x(6≤x<15).
17.y=﹣10x2+100x+6000.
18.0.5米.
19.25.
20.解:设P.Q同时出发后经过的时间为t秒,四边形APQC的面积为S平方毫米,
则有:S=S△ABC-S△PBQ
=
=4t2-24t+144
=4(t-3)2+108.
∵4>0
∴当t=3s时,S取得最小值.
21.解:(1)设购进荔枝a千克,荔枝售价定为b元/千克时,水果商才不会亏本,由题意得
ba(1-5%)≥(5+0.7)a,
∵a>0,
∴95%b≥5.7
∴b≥6
所以,水果商要把荔枝售价至少定为6元/千克才不会亏本.
(2)由(1)可知,每千克荔枝的平均成本为6元,由题意得
w=(x-6)m
=(x-6)(-10x+120)
=
-10(x-9)2+90,
∵a=
-10<0
∴w有最大值
∴当x=9时,w有最大值.
所以,当销售单价定为9元/千克时,每天可获利润w最大.
22.解:(1)设A到BC的距离为d
cm,E到BC的距离为h
cm,则y=S平行四边形BDEF=xh.∵S△ABC=BC·d,∴2400=×80d,∴d=60.∵ED∥AB,∴△EDC∽△ABC,∴,即,∴h=,∴y=x=-x2+60x.(2)自变量x的取值范围是0<x<80.
(3)∵a=-<0,-=40,0<40<80,∴当x=40时,y最大值=1200.
23.解:(1)设直线AB的解析式为y=kx+b(k≠0),
将点A(0,6),B(6,0)代入y=kx+b(k≠0),得,
∴,
则直线AB的解析式为y=﹣x+6;
(2)∵抛物线过点B(6,0),C(﹣2,0),
∴设抛物线的解析式为y=a(x﹣6)(x+2)(a≠0),
将点A(0,6)代入y=a(x﹣6)(x+2),得﹣12a=6,
解得a=﹣,
∴抛物线的解析式为y=﹣(x﹣6)(x+2)=﹣x2+2x+6;
(3)如图,
过点P作PN∥y轴,交AB于N,
设P点坐标为(t,﹣t2+2t+6)(0<t<6),
则N(t,﹣t+6),
∴PN=yP﹣yN=﹣t2+2t+6﹣(﹣t+6)=﹣t2+2t+6+t﹣6=﹣t2+3t.
∴S△PAB=S△PAN+S△PBN
=PN?|xP﹣xA|+PN?|xB﹣xP|
=PN?(xB﹣xA)=×(﹣t2+3t)×6
=﹣(t﹣3)2+,
∴当t=3,即点P位于(3,)时,△PAB的面积有最大值.
24.解:(1)∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为y=ax2,
将点A(1,)代入y=ax2得:a=,
∴二次函数的解析式为y=x2;
(2)证明:∵点P在抛物线y=x2上,
∴可设点P的坐标为(x,x2),
如图,过点P作PB⊥y轴于点B,则BF=x2﹣1,PB=x,
∴Rt△BPF中,
PF==x2+1,
∵PM⊥直线y=﹣1,
∴PM=x2+1,
∴PF=PM,
∴∠PFM=∠PMF,
又∵PM∥x轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP;
(3)当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,
∴x2+1=4,
解得:x=±2,
∴x2=×12=3,
∴满足条件的点P的坐标为(2,3)或(﹣2,3).
25.解:(1)点C的坐标为(0,1),b=1,
将点B坐标代入代入一次函数表达式得:3=4k+1,解得:k=,
则一次函数表达式为:y=x+1,则点A坐标为(﹣2,0),
把点C.B坐标代入二次函数表达式得:3=a×42﹣4(6a﹣2)+1,解得:a=,
则二次函数表达式为:y=x2﹣x+1;
(2)①如下图,当∠AQB=90°时,
△ABQ与△AOC相似,m=4,
②当∠ABQ=90°时,△ABQ与△AOC相似,
AB==3,cos∠BAO==,
则AQ==,
则m=﹣2=,
即:m的值为4或.
26.解:(1)∵A(﹣1,0),C(0,﹣3)在y=x2+bx+c上,
则,解得,
∴二次函数的解析式为y=x2﹣2x﹣3;
(2)在y=x2﹣2x﹣3中,令y=0可得0=x2﹣2x﹣3,解得x=3或x=﹣1,
∴B(3,0),且C(0,﹣3),
∴经过B.C两点的直线为y=x﹣3,
设点P的坐标为(x,x2﹣2x﹣3),如图,过点P作PD⊥x轴,垂足为D,与直线BC交于点E,则E(x,x﹣3),
∵S四边形ABPC=S△ABC+S△BCP=×4×3+(3x﹣x2)×3=﹣x2+x+6=﹣(x﹣)2+,
∴当x=时,四边形ABPC的面积最大,此时P点坐标为(,﹣),
∴四边形ABPC的最大面积为;
(3)点A关于函数对称轴的对称点为点B,连接BC交函数对称轴于点Q,连接AQ,则此时△QAC的周长最小,
理由:△QAC的周长=AC+AQ+QC=AB+AQ+QC=BC+CQ为最小,
由点B.C的坐标得,直线BC的表达式为y=x﹣3,
当x=1时,y=x﹣3=﹣2,即点Q(1,﹣2),
则△QAC的周长最小值=BC+AC=3+=3+.
