北师大版九年级数学下册课件:2.2 二次函数的图像与性质(共31张PPT)
文档属性
| 名称 | 北师大版九年级数学下册课件:2.2 二次函数的图像与性质(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-16 12:27:15 | ||
图片预览










文档简介
第一讲:二次函数的图像与性质
教学内容:
1.二次函数的概念
2.y=ax2的图像与性质
3.y= 的图像与性质
4.y= 的图像与性质
5.y= 的图像与性质
6.y =a x? + b x + c的图像与性质
二次函数:
y = k x+ b (k≠0)
y = k x (k≠0)
一次函数
变量之间的关系
函数
反比例函数
正比例函数
y = (k≠0)
温故知新
1.一般地,形如y =a x? + b x + c (a、b、c是常数,a≠0)的函数叫做 x 的二次函数(图像为抛物线).
1.二次函数的概念:
例1:当m为何值时,函数y= 是二次函数
2.2.y=x2与y=-x2 的图像与性质
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
y
x
-1
-2
-3
O
1
2
3
-6
-7
-8
-3
-4
-5
-9
-1
-2
y=- x2
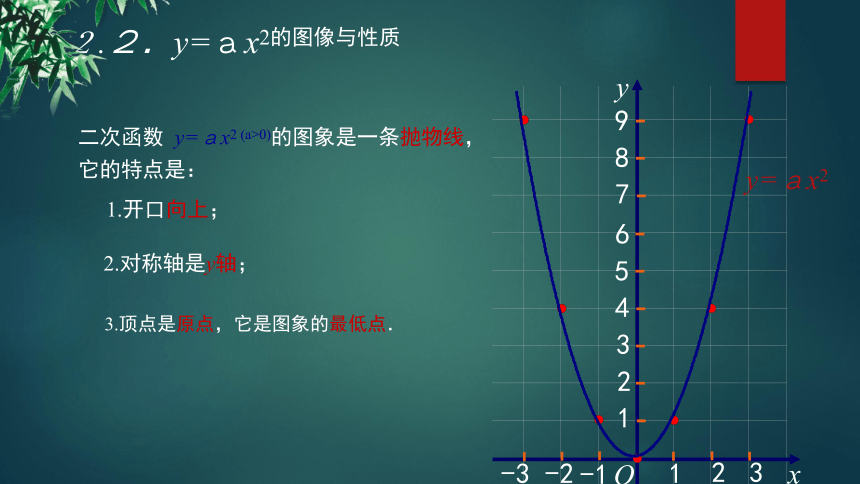
二次函数 y=ax2 (a>0)的图象是一条抛物线,它的特点是:
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=ax2
1.开口向上;
2.对称轴是y轴;
3.顶点是原点,它是图象的最低点.
2.2.y=ax2的图像与性质
例2.抛物线 y=ax2 与 y=x2 的开口大小、形状一样、开口方向相反,则 a = .
例3.点 A(2,a),B(b,9)在抛物线 y=x2 上,则 a = ,b = .
-1
4
±3
例5.二次函数 y = -x2 的图象,在 y 轴的右边,y 随 x 的增大而________.
减小
例4.若点 A(2,m)在抛物线 y=x2 上,则点A关于 y 轴对称点的坐标是 .
(-2,4)
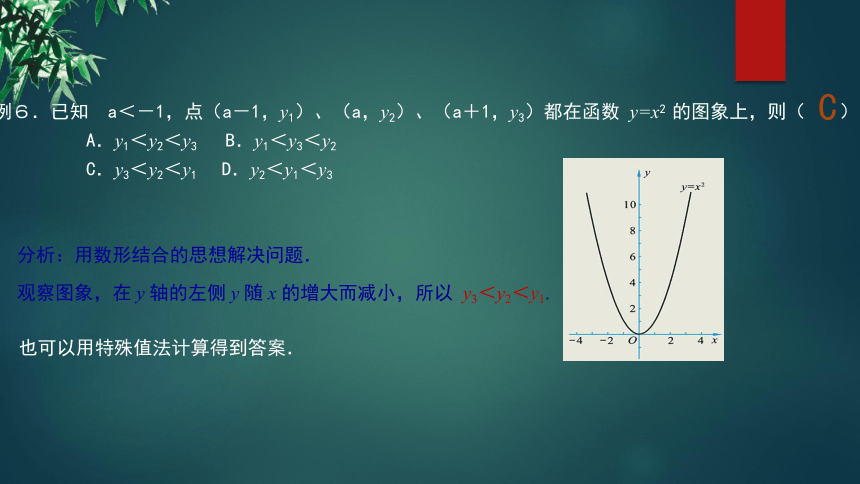
例6.已知 a<-1,点(a-1,y1)、(a,y2)、(a+1,y3)都在函数 y=x2 的图象上,则(????? )
A.y1<y2<y3 B.y1<y3<y2?????
C.y3<y2<y1 D.y2<y1<y3
C
分析:用数形结合的思想解决问题.
观察图象,在 y 轴的左侧 y 随 x 的增大而减小,所以 y3<y2<y1.
也可以用特殊值法计算得到答案.
3.1. y=x2 +1与y=-x2 -1的图像与性质
1.向上向下平移
2. 顶点坐标(0,1),(0.-1)
3.2. y=ax2 +c与y=-x2 +c的图像与性质
1.平移:上加下减
2.顶点坐标(0,c)
4. 的图像与性质
1.平移:左加右减
2.顶点坐标(h,0)
5.1 的图像与性质
1.平移:上加下减,左加右减
2.顶点坐标(h,k)
5.2 的图像与性质
y=ax2
6.y =a x? + b x + c的图像与性质
当a>0,开口向上
当a<0,开口向上
例7.把函数y=3x2+6x+10转化成y=a(x-h)2+k的形式,然后指出它的图象开口方向,对称轴,顶点坐标和最值.
例8.求函数y=3x2+6x+10(x≥4)的最小值
例9.已知点(3, )(4, ), (5, )在函数y=2x2+8x+7的图象上,则他们大小大小关系是( )
A、y1>y2>y3
B、y2> y1> y3
C、y2>y3> y1 D、y3> y2> y1
A.
B.
C.
D.
例10.二次函数y=ax2+bx+c的图像如图所示,反比例函数 与正比例函数y=(b+c)x在同一坐标系中的大致图像可能是(??? ?)
例11.在同一坐标系中,二次函数 与一次函数 的图像可能是( )
A.
B.
C.
D.
A.
例12.如图,四个二次函数的图象中,分别对应的是:
① ;② ;③ ;④ , 则的大小关系为
13.如图,抛物线 的对称轴是直线x=1,且经过点P(3,0),a-b+c的值为————
例14.如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
A.abc>0 B.a+b+c<0
C.b<a+c D.4a+2b+c>0
例15.若二次函数y=ax2+bx+c 的x与y的部分对应值如下表,则当x=1时,y的值为
例16.已知二次函数 ,函数y与自变量x的部分对应值如下表所示,下列
说法错误的是( )
A.图象开口向下 B.抛物线的对称轴是直线x=2
C.
D.当y<6时,1<x<3
例17.已知抛物线 经过点 和(-a, y1 ),则y1的值是_________.
例18.将抛物线 的解析式向上平移3个单位长度,在向右平移1个单位长度后,得到的抛物线的解析式是 .
例19.如果二次函数y=(-2k+4)x2-3x+1的图象开口向上,那么常数k的取值范围是________
k<2
例20.已知函数y=(k﹣2)xk?﹣4k+5+2x是关于x的二次函数.求:
(1)满足条件的k的值;
(2)当k为何值时,抛物线有最高点?求出这个最高点,这时,x为何值时,y随x的增大而增大?
K=1或k=3
例21.已知抛物线y= +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
m=2顶点坐标为:(1,4).
课堂小结:
谢谢观看
教学内容:
1.二次函数的概念
2.y=ax2的图像与性质
3.y= 的图像与性质
4.y= 的图像与性质
5.y= 的图像与性质
6.y =a x? + b x + c的图像与性质
二次函数:
y = k x+ b (k≠0)
y = k x (k≠0)
一次函数
变量之间的关系
函数
反比例函数
正比例函数
y = (k≠0)
温故知新
1.一般地,形如y =a x? + b x + c (a、b、c是常数,a≠0)的函数叫做 x 的二次函数(图像为抛物线).
1.二次函数的概念:
例1:当m为何值时,函数y= 是二次函数
2.2.y=x2与y=-x2 的图像与性质
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=x2
y
x
-1
-2
-3
O
1
2
3
-6
-7
-8
-3
-4
-5
-9
-1
-2
y=- x2
二次函数 y=ax2 (a>0)的图象是一条抛物线,它的特点是:
x
y
-1
-2
-3
O
1
2
3
3
2
1
6
5
4
9
8
7
y=ax2
1.开口向上;
2.对称轴是y轴;
3.顶点是原点,它是图象的最低点.
2.2.y=ax2的图像与性质
例2.抛物线 y=ax2 与 y=x2 的开口大小、形状一样、开口方向相反,则 a = .
例3.点 A(2,a),B(b,9)在抛物线 y=x2 上,则 a = ,b = .
-1
4
±3
例5.二次函数 y = -x2 的图象,在 y 轴的右边,y 随 x 的增大而________.
减小
例4.若点 A(2,m)在抛物线 y=x2 上,则点A关于 y 轴对称点的坐标是 .
(-2,4)
例6.已知 a<-1,点(a-1,y1)、(a,y2)、(a+1,y3)都在函数 y=x2 的图象上,则(????? )
A.y1<y2<y3 B.y1<y3<y2?????
C.y3<y2<y1 D.y2<y1<y3
C
分析:用数形结合的思想解决问题.
观察图象,在 y 轴的左侧 y 随 x 的增大而减小,所以 y3<y2<y1.
也可以用特殊值法计算得到答案.
3.1. y=x2 +1与y=-x2 -1的图像与性质
1.向上向下平移
2. 顶点坐标(0,1),(0.-1)
3.2. y=ax2 +c与y=-x2 +c的图像与性质
1.平移:上加下减
2.顶点坐标(0,c)
4. 的图像与性质
1.平移:左加右减
2.顶点坐标(h,0)
5.1 的图像与性质
1.平移:上加下减,左加右减
2.顶点坐标(h,k)
5.2 的图像与性质
y=ax2
6.y =a x? + b x + c的图像与性质
当a>0,开口向上
当a<0,开口向上
例7.把函数y=3x2+6x+10转化成y=a(x-h)2+k的形式,然后指出它的图象开口方向,对称轴,顶点坐标和最值.
例8.求函数y=3x2+6x+10(x≥4)的最小值
例9.已知点(3, )(4, ), (5, )在函数y=2x2+8x+7的图象上,则他们大小大小关系是( )
A、y1>y2>y3
B、y2> y1> y3
C、y2>y3> y1 D、y3> y2> y1
A.
B.
C.
D.
例10.二次函数y=ax2+bx+c的图像如图所示,反比例函数 与正比例函数y=(b+c)x在同一坐标系中的大致图像可能是(??? ?)
例11.在同一坐标系中,二次函数 与一次函数 的图像可能是( )
A.
B.
C.
D.
A.
例12.如图,四个二次函数的图象中,分别对应的是:
① ;② ;③ ;④ , 则的大小关系为
13.如图,抛物线 的对称轴是直线x=1,且经过点P(3,0),a-b+c的值为————
例14.如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
A.abc>0 B.a+b+c<0
C.b<a+c D.4a+2b+c>0
例15.若二次函数y=ax2+bx+c 的x与y的部分对应值如下表,则当x=1时,y的值为
例16.已知二次函数 ,函数y与自变量x的部分对应值如下表所示,下列
说法错误的是( )
A.图象开口向下 B.抛物线的对称轴是直线x=2
C.
D.当y<6时,1<x<3
例17.已知抛物线 经过点 和(-a, y1 ),则y1的值是_________.
例18.将抛物线 的解析式向上平移3个单位长度,在向右平移1个单位长度后,得到的抛物线的解析式是 .
例19.如果二次函数y=(-2k+4)x2-3x+1的图象开口向上,那么常数k的取值范围是________
k<2
例20.已知函数y=(k﹣2)xk?﹣4k+5+2x是关于x的二次函数.求:
(1)满足条件的k的值;
(2)当k为何值时,抛物线有最高点?求出这个最高点,这时,x为何值时,y随x的增大而增大?
K=1或k=3
例21.已知抛物线y= +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
m=2顶点坐标为:(1,4).
课堂小结:
谢谢观看
