北师大版九年级数学下册 第三章: 圆的基本性质 课件(共27张PPT)
文档属性
| 名称 | 北师大版九年级数学下册 第三章: 圆的基本性质 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 46.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 09:06:22 | ||
图片预览


文档简介
第21讲 圆的基本性质
(必考,1~3道,4~17分)
垂径定理的相关计算(2016.14)
命题点
1
玩转贵阳10年中考真题
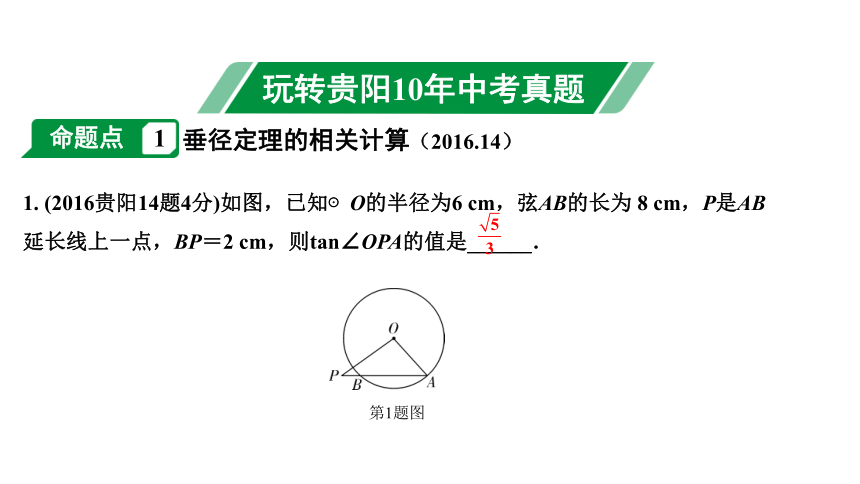
1. (2016贵阳14题4分)如图,已知⊙O的半径为6 cm,弦AB的长为 8 cm,P是AB延长线上一点,BP=2 cm,则tan∠OPA的值是______.
第1题图
拓展训练
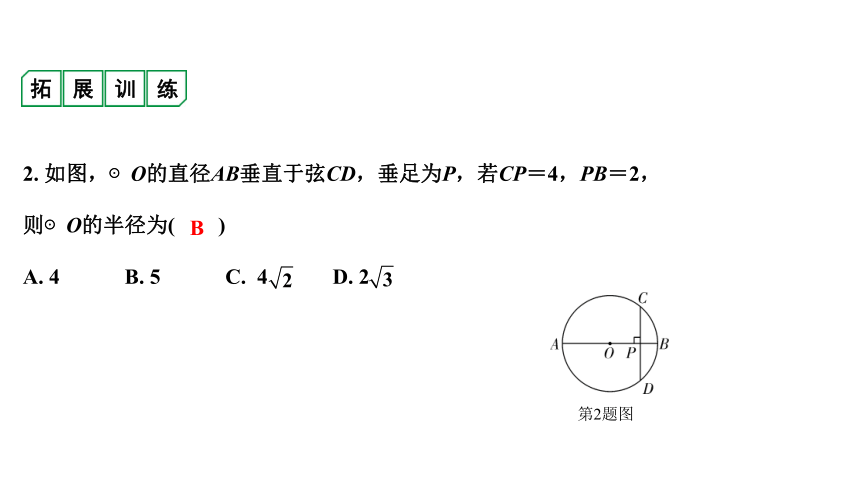
2. 如图,⊙O的直径AB垂直于弦CD,垂足为P,若CP=4,PB=2,
则⊙O的半径为( )
A. 4 B. 5 C. 4 D. 2
第2题图
B
与圆周角定理有关的计算(10年5考)
命题点
2
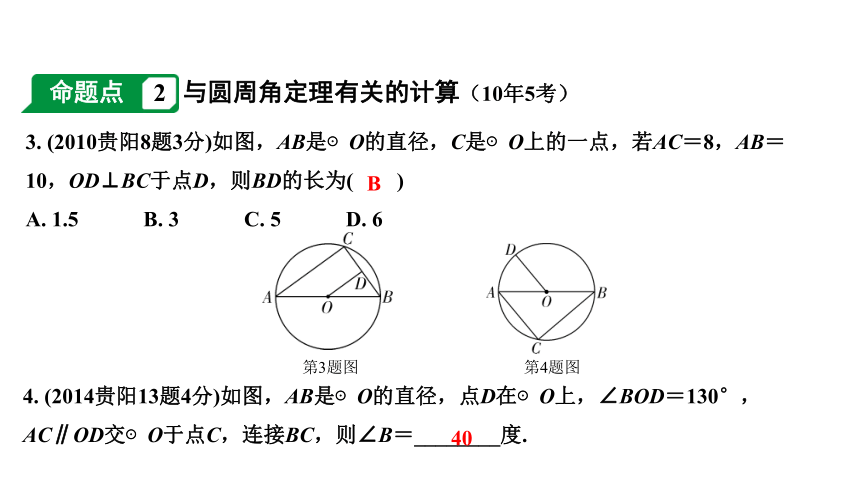
3. (2010贵阳8题3分)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )
A. 1.5 B. 3 C. 5 D. 6
4. (2014贵阳13题4分)如图,AB是⊙O的直径,点D在⊙O上,∠BOD=130°,AC∥OD交⊙O于点C,连接BC,则∠B=________度.
第3题图
第4题图
B
40
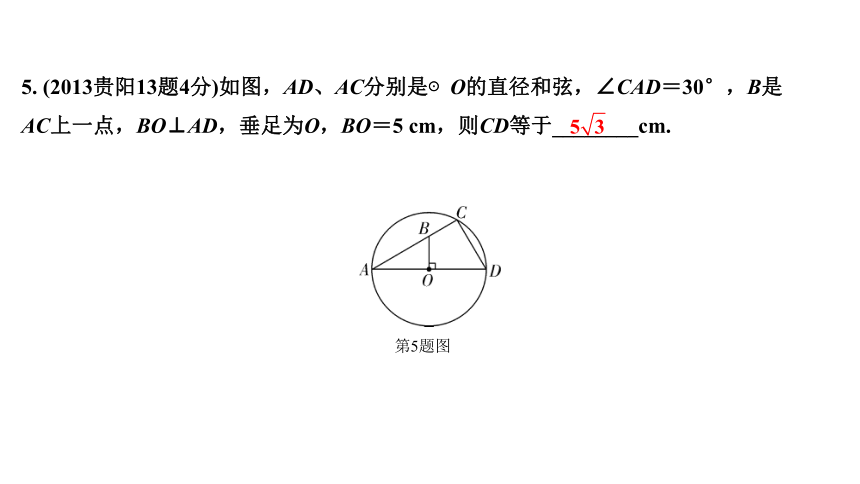
5. (2013贵阳13题4分)如图,AD、AC分别是⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5 cm,则CD等于________cm.
第5题图
拓展训练
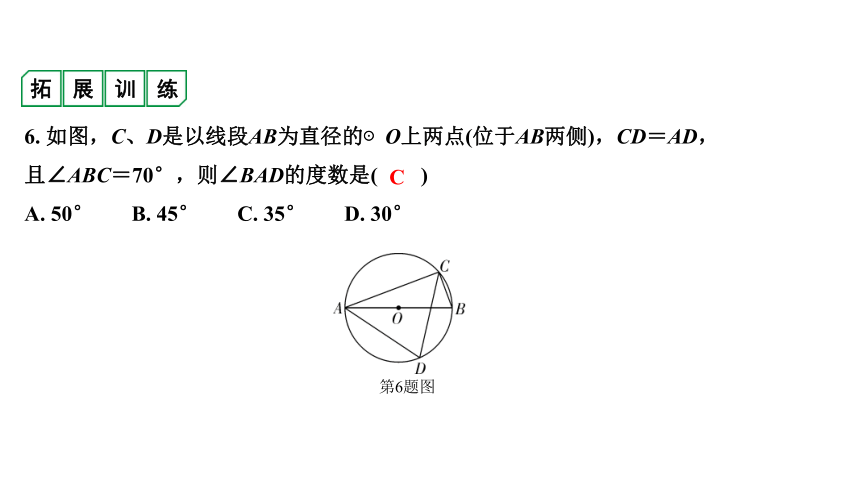
6. 如图,C、D是以线段AB为直径的⊙O上两点(位于AB两侧),CD=AD,
且∠ABC=70°,则∠BAD的度数是( )
A. 50° B. 45° C. 35° D. 30°
第6题图
C
正多边形与圆的相关计算(近5年每年必考一道选择题或填空题)
命题点
3
7. (2019贵阳6题3分)如图,正六边形ABCDEF内接于⊙O,连接BD,
则∠CBD的度数是( )
A. 30° B. 45°
C. 60° D. 90°
8. (2016贵阳8题3分)小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上.若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A. 2 cm B. 4 cm
C. 6 cm D. 8 cm
A
B
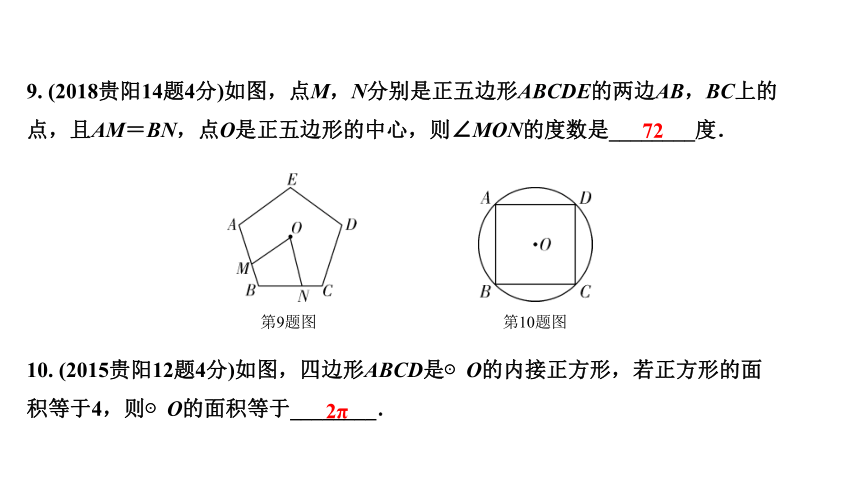
9. (2018贵阳14题4分)如图,点M,N分别是正五边形ABCDE的两边AB,BC上的点,且AM=BN,点O是正五边形的中心,则∠MON的度数是________度.
10. (2015贵阳12题4分)如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于________.
第9题图
第10题图
72
2π
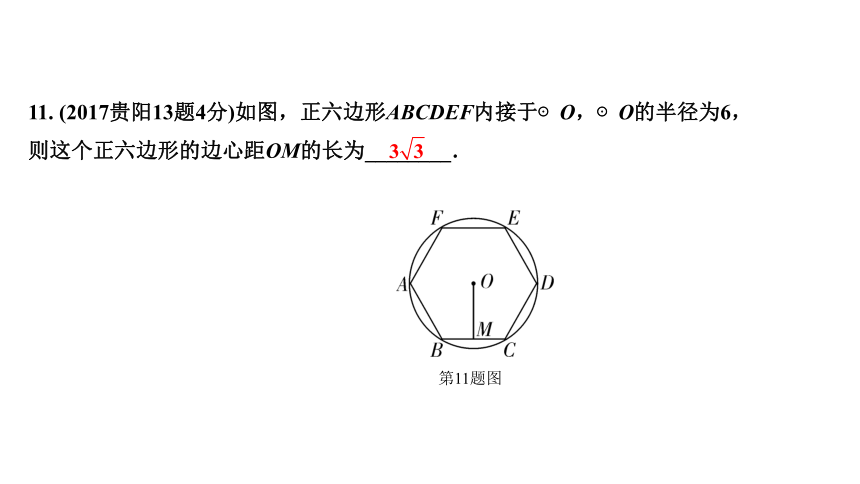
11. (2017贵阳13题4分)如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为________.
第11题图
圆的基本性质
圆内接四边形的性质
正多边形和圆的关系
垂径理论及其推论
圆的定义
圆的有关概念及性质
有关概念
性质
弦、弧、圆心角的关系
定理
推论
圆周角定理及其推论
定理
推论
三角形的
外接圆
圆心O名称
性质
角度关系
考点精讲
圆的有关概念及性质
性质
圆的定义:圆是所有到定点的距离等于定长的点的集合
有关概念
圆心角:顶点在圆心的角,如图①中的∠BOC,∠AOC,
圆周角:顶点在圆上,并且两边都和圆相交的角,
如图①中的∠BAC,
弦:连接圆上任意两点的线段叫做弦;经过圆心的弦叫做_______, 如图①中的AB
圆弧:圆上任意两点间的部分,如图①中的优弧 劣弧
1.圆是轴对称图形,任意一条直径都是它的对称轴
2.圆也是中心对称图形, 是它的对称中心
对称性
旋转不变性:圆绕圆心旋转任意角度都与自身重合
图①
直径
圆心
返回思维导图
名称
文字描述
(数学符号如图②)
垂径
定理
垂直于弦的直径平分弦,并且平分弦所对的弧
CD⊥AB
CD是直径
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧
_________
CD是直径
总结:根据圆的对称性,在以下五个结论中:① ;② ;③AM=BM;④AB⊥CD;⑤CD是直径.只要满足其中两个结论,另外三个结论一定成立,即“知二推三”
?
AM=BM= AB
?
CD= AB
应用:如图②,半径(OB)、弦心距(OM)和弦的一半(MB)构成直角三角形,满足勾股定理, OB2=OM2+BM2,常用于圆中求线段的长
AM=BM
⊥
垂径定理及其推论
图②
返回思维导图
弦、弧、圆心角的关系
定理:在同圆或等圆中,相等的圆心角所对的弧_______,所对的弦也相等,所对弦的弦心距也相等
推论:在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量, 都分别_______
内容
_____________________________________________________
情况
圆心在圆周角的一条边上
圆心在圆周角的内部
圆心在圆周角的外部
图形
结论
∠APB=_____∠AOB
圆周角定理及其推论
定理
相等
相等
圆周角的度数等于它所对弧上的圆心角度数的一半
返回思维导图
文字描述
数学符号(如图③)
作用
推论1
同弧或等弧所对的圆周角相等
证明圆周角相等
推论2
直径所对的圆周角是_________,90°的圆周角所对的弦是________
1.AB是直径?∠ACB=
_________;
2.∠ACB=_________?AB是直径
(1)连接弦,直径所对的圆周角为直角,得到直角三角形;
(2)确定圆的直径
1.∠A和_______是 所对的
圆周角?∠A=_______
2. ?∠A=_______
∠D
∠D
∠BCD
直角
直径
90°
90°
推论
图③
圆周角定理及其推论
返回思维导图
三角形的外接圆
(1)圆心O名称:外心,即三角形三条边的___________的交点
(2)性质:三角形的外心到三角形___________________
(3)角度关系:∠BOC=2∠A
如图④
圆内接四边形的
性质
1.圆内接四边形的对角互补,如图⑤,∠A+∠BCD= ________,∠B+∠D=________
2.圆内接四边形的任意一个角的外角等于它的内对角,
如图⑤,∠DCE=________
正多边形和圆
的关系
1. 设正n边形的边长为a,则边心距
2. 正n边形的周长l=na;正n边形面积
3. 中心角θ=
如图⑥
图⑤
图④
图⑥
垂直平分线
三个顶点的距离相等
180°
180°
∠A
返回思维导图
重难点突破
一、垂径定理的证明与计算
①②③⑤⑦⑧⑨?
例1 如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD于点E.
(1)连接AC,BC,AD,BD,OC,则下列结论正确的是__________________(填序号);
①CE=DE;② ;③BC=BD;④△OCB是等边三角形;⑤∠ACB=∠ADB=90°;⑥∠COB=3∠CDB;⑦△ADC是等腰三角形;⑧△ABC≌△ABD;⑨∠CDB=∠ACO;⑩CD2=4AE·AB;?DE2=AE·BE.
(2)把上述错误的结论改正确;
(3)若∠CAB=22.5°,AB=4,求CD的长;
(2)④△OCB是等腰三角形,⑥∠COB=2∠CDB,⑩CD2=4AE·BE;
例1题图
(3)∵∠CAB=22.5°,
∴∠COB=2∠CAB=45°,
∵AB=4,
∴OC= AB=2,
∵AB⊥CD,
∴∠OEC=90°,CD=2CE,
∴∠OCE=45°,OE=CE,
在Rt△COE中,
∵OE2+CE2=OC2,
∴2CE2=4,
∴CE= ,
∴CD=2CE=2 ;
(4)若CD=18,AE∶EB=9∶1,求AB的长.
(4)∵AB⊥CD,CD=18,
∴∠AEC=∠CEB=90°, ,
CE=DE= CD= ×18=9,
∵∠CAE+∠ACE=90°,∠BCE+∠ACE=90°,
∴∠CAE=∠ECB,
∴△AEC∽△CEB,
【思维教练】结合已知及所求AB恰好位于“母子型”相似模型Rt△ACB中,故构造Rt△AEC∽Rt△CEB,即可求解.
∴
即CE2=AE·EB,
∵AE∶EB=9∶1,
∴设EB的长为x,则AE为9x,
∴92=9x·x,
解得x1=-3(不合题意,舍去),x2=3,
∴AE=27,EB=3,
∴AB=AE+EB=27+3=30.
运用垂径定理解题时应注意:
1. 两条辅助线:(1)过圆心作弦的垂线,(2)连接圆心和弦的一端(即半径),这样把半径、弦心距、弦的一半构建在一个直角三角形中,运用勾股定理求解;
2. 方程思想:在直接运用垂径定理求线段的长度时,常将未知的一条线段设为x,利用勾股定理构造关于x的方程解决问题,这是一种用代数方法解决几何问题的解题思路.另外,在圆中求线段长,三角形相似也是常用的方法.
满分技法
二、圆周角定理的证明与计算
例2 如图,△ABC内接于⊙O,BC为⊙O的直径.
(1)如图①,∠CAB=________°;
(2)如图②,连接OA,若∠AOB=60°,则∠ACB=______°;
(3)如图③, P为⊙O上一点,连接AP,BP,∠ACB=30°,则∠APB=________°,若B为 的中点,则∠PAB=________°;
(4)如图④,P为 上一点,∠P=30°,AC=2,则∠ACB=_____°;AB=____.
例2题图①
例2题图②
例2题图③
例2题图④
90
30
30
30
60
练习1 如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数
为( )
A. 25°
B. 30°
C. 50°
D. 60°
练习1题图
C
练习2 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是 上任意一点,
延长AG与DC的延长线交于点F,连接AD,GD,CG.
(1)求证:∠AGD=∠FGC;
(2)若AG=12,GF=4,CD=4 ,求⊙O的半径.
练习2题图
练习2 (1)证明:如解图,连接AC、BC,
∵AB⊥CD,
∴EC=ED,
∴AC=AD,
∴∠3=∠ADC,
∵∠1+∠AGC=180°,∠AGC+∠ADC=180°,
∴∠1=∠ADC,
∵∠2=∠3,
∴∠1=∠2,
即∠AGD=∠FGC;
练习2题解图
(2)解:如解图,∵∠FCG+∠DCG=180°,∠DCG+∠DAG=180°,
∴∠FCG=∠DAG,
∵∠1=∠2,
∴∠ADG=∠F,
∵∠ADG=∠ACG,
∴∠ACG=∠F,
∵∠CAG=∠CAF,
∴△CAG∽△FAC,
∴
∴AC2=AG·AF=192,
∴AC=8,
在Rt△ACE中,
∵∠AEC=90°,AC=8 ,CE=2 ,
∴AE=
易知△ACE∽△ABC,
∴
∴AC2=AE·AB,
∴AB=
∴⊙O的半径为
满分技法
1. 如图①,四边形ABCD是⊙O的内接四边形,AC、BD是⊙O的两条弦,根据同弧所对
的圆周角相等和对顶角相等可得到①△ABM∽△DCM;②△BCM∽△ADM,从而得到
(MA·MC=MB·MD).
2. 如图②,延长四边形ABCD的边BA、CD交于点P,根据圆内接四边形的性质∠PAD=∠BCD,∠PDA=∠ABC,可得到△PDA∽△PBC, ,而AD和BC分别在△ADM和△BCM中,且△ADM∽△BCM,从而得到更多的线段关系.
3. 如图③,当AC⊥BD时,恰好构成垂径定理的基本图形,适用于与其相关的所有结论.
(必考,1~3道,4~17分)
垂径定理的相关计算(2016.14)
命题点
1
玩转贵阳10年中考真题
1. (2016贵阳14题4分)如图,已知⊙O的半径为6 cm,弦AB的长为 8 cm,P是AB延长线上一点,BP=2 cm,则tan∠OPA的值是______.
第1题图
拓展训练
2. 如图,⊙O的直径AB垂直于弦CD,垂足为P,若CP=4,PB=2,
则⊙O的半径为( )
A. 4 B. 5 C. 4 D. 2
第2题图
B
与圆周角定理有关的计算(10年5考)
命题点
2
3. (2010贵阳8题3分)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )
A. 1.5 B. 3 C. 5 D. 6
4. (2014贵阳13题4分)如图,AB是⊙O的直径,点D在⊙O上,∠BOD=130°,AC∥OD交⊙O于点C,连接BC,则∠B=________度.
第3题图
第4题图
B
40
5. (2013贵阳13题4分)如图,AD、AC分别是⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5 cm,则CD等于________cm.
第5题图
拓展训练
6. 如图,C、D是以线段AB为直径的⊙O上两点(位于AB两侧),CD=AD,
且∠ABC=70°,则∠BAD的度数是( )
A. 50° B. 45° C. 35° D. 30°
第6题图
C
正多边形与圆的相关计算(近5年每年必考一道选择题或填空题)
命题点
3
7. (2019贵阳6题3分)如图,正六边形ABCDEF内接于⊙O,连接BD,
则∠CBD的度数是( )
A. 30° B. 45°
C. 60° D. 90°
8. (2016贵阳8题3分)小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上.若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A. 2 cm B. 4 cm
C. 6 cm D. 8 cm
A
B
9. (2018贵阳14题4分)如图,点M,N分别是正五边形ABCDE的两边AB,BC上的点,且AM=BN,点O是正五边形的中心,则∠MON的度数是________度.
10. (2015贵阳12题4分)如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于________.
第9题图
第10题图
72
2π
11. (2017贵阳13题4分)如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为________.
第11题图
圆的基本性质
圆内接四边形的性质
正多边形和圆的关系
垂径理论及其推论
圆的定义
圆的有关概念及性质
有关概念
性质
弦、弧、圆心角的关系
定理
推论
圆周角定理及其推论
定理
推论
三角形的
外接圆
圆心O名称
性质
角度关系
考点精讲
圆的有关概念及性质
性质
圆的定义:圆是所有到定点的距离等于定长的点的集合
有关概念
圆心角:顶点在圆心的角,如图①中的∠BOC,∠AOC,
圆周角:顶点在圆上,并且两边都和圆相交的角,
如图①中的∠BAC,
弦:连接圆上任意两点的线段叫做弦;经过圆心的弦叫做_______, 如图①中的AB
圆弧:圆上任意两点间的部分,如图①中的优弧 劣弧
1.圆是轴对称图形,任意一条直径都是它的对称轴
2.圆也是中心对称图形, 是它的对称中心
对称性
旋转不变性:圆绕圆心旋转任意角度都与自身重合
图①
直径
圆心
返回思维导图
名称
文字描述
(数学符号如图②)
垂径
定理
垂直于弦的直径平分弦,并且平分弦所对的弧
CD⊥AB
CD是直径
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧
_________
CD是直径
总结:根据圆的对称性,在以下五个结论中:① ;② ;③AM=BM;④AB⊥CD;⑤CD是直径.只要满足其中两个结论,另外三个结论一定成立,即“知二推三”
?
AM=BM= AB
?
CD= AB
应用:如图②,半径(OB)、弦心距(OM)和弦的一半(MB)构成直角三角形,满足勾股定理, OB2=OM2+BM2,常用于圆中求线段的长
AM=BM
⊥
垂径定理及其推论
图②
返回思维导图
弦、弧、圆心角的关系
定理:在同圆或等圆中,相等的圆心角所对的弧_______,所对的弦也相等,所对弦的弦心距也相等
推论:在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量, 都分别_______
内容
_____________________________________________________
情况
圆心在圆周角的一条边上
圆心在圆周角的内部
圆心在圆周角的外部
图形
结论
∠APB=_____∠AOB
圆周角定理及其推论
定理
相等
相等
圆周角的度数等于它所对弧上的圆心角度数的一半
返回思维导图
文字描述
数学符号(如图③)
作用
推论1
同弧或等弧所对的圆周角相等
证明圆周角相等
推论2
直径所对的圆周角是_________,90°的圆周角所对的弦是________
1.AB是直径?∠ACB=
_________;
2.∠ACB=_________?AB是直径
(1)连接弦,直径所对的圆周角为直角,得到直角三角形;
(2)确定圆的直径
1.∠A和_______是 所对的
圆周角?∠A=_______
2. ?∠A=_______
∠D
∠D
∠BCD
直角
直径
90°
90°
推论
图③
圆周角定理及其推论
返回思维导图
三角形的外接圆
(1)圆心O名称:外心,即三角形三条边的___________的交点
(2)性质:三角形的外心到三角形___________________
(3)角度关系:∠BOC=2∠A
如图④
圆内接四边形的
性质
1.圆内接四边形的对角互补,如图⑤,∠A+∠BCD= ________,∠B+∠D=________
2.圆内接四边形的任意一个角的外角等于它的内对角,
如图⑤,∠DCE=________
正多边形和圆
的关系
1. 设正n边形的边长为a,则边心距
2. 正n边形的周长l=na;正n边形面积
3. 中心角θ=
如图⑥
图⑤
图④
图⑥
垂直平分线
三个顶点的距离相等
180°
180°
∠A
返回思维导图
重难点突破
一、垂径定理的证明与计算
①②③⑤⑦⑧⑨?
例1 如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD于点E.
(1)连接AC,BC,AD,BD,OC,则下列结论正确的是__________________(填序号);
①CE=DE;② ;③BC=BD;④△OCB是等边三角形;⑤∠ACB=∠ADB=90°;⑥∠COB=3∠CDB;⑦△ADC是等腰三角形;⑧△ABC≌△ABD;⑨∠CDB=∠ACO;⑩CD2=4AE·AB;?DE2=AE·BE.
(2)把上述错误的结论改正确;
(3)若∠CAB=22.5°,AB=4,求CD的长;
(2)④△OCB是等腰三角形,⑥∠COB=2∠CDB,⑩CD2=4AE·BE;
例1题图
(3)∵∠CAB=22.5°,
∴∠COB=2∠CAB=45°,
∵AB=4,
∴OC= AB=2,
∵AB⊥CD,
∴∠OEC=90°,CD=2CE,
∴∠OCE=45°,OE=CE,
在Rt△COE中,
∵OE2+CE2=OC2,
∴2CE2=4,
∴CE= ,
∴CD=2CE=2 ;
(4)若CD=18,AE∶EB=9∶1,求AB的长.
(4)∵AB⊥CD,CD=18,
∴∠AEC=∠CEB=90°, ,
CE=DE= CD= ×18=9,
∵∠CAE+∠ACE=90°,∠BCE+∠ACE=90°,
∴∠CAE=∠ECB,
∴△AEC∽△CEB,
【思维教练】结合已知及所求AB恰好位于“母子型”相似模型Rt△ACB中,故构造Rt△AEC∽Rt△CEB,即可求解.
∴
即CE2=AE·EB,
∵AE∶EB=9∶1,
∴设EB的长为x,则AE为9x,
∴92=9x·x,
解得x1=-3(不合题意,舍去),x2=3,
∴AE=27,EB=3,
∴AB=AE+EB=27+3=30.
运用垂径定理解题时应注意:
1. 两条辅助线:(1)过圆心作弦的垂线,(2)连接圆心和弦的一端(即半径),这样把半径、弦心距、弦的一半构建在一个直角三角形中,运用勾股定理求解;
2. 方程思想:在直接运用垂径定理求线段的长度时,常将未知的一条线段设为x,利用勾股定理构造关于x的方程解决问题,这是一种用代数方法解决几何问题的解题思路.另外,在圆中求线段长,三角形相似也是常用的方法.
满分技法
二、圆周角定理的证明与计算
例2 如图,△ABC内接于⊙O,BC为⊙O的直径.
(1)如图①,∠CAB=________°;
(2)如图②,连接OA,若∠AOB=60°,则∠ACB=______°;
(3)如图③, P为⊙O上一点,连接AP,BP,∠ACB=30°,则∠APB=________°,若B为 的中点,则∠PAB=________°;
(4)如图④,P为 上一点,∠P=30°,AC=2,则∠ACB=_____°;AB=____.
例2题图①
例2题图②
例2题图③
例2题图④
90
30
30
30
60
练习1 如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数
为( )
A. 25°
B. 30°
C. 50°
D. 60°
练习1题图
C
练习2 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是 上任意一点,
延长AG与DC的延长线交于点F,连接AD,GD,CG.
(1)求证:∠AGD=∠FGC;
(2)若AG=12,GF=4,CD=4 ,求⊙O的半径.
练习2题图
练习2 (1)证明:如解图,连接AC、BC,
∵AB⊥CD,
∴EC=ED,
∴AC=AD,
∴∠3=∠ADC,
∵∠1+∠AGC=180°,∠AGC+∠ADC=180°,
∴∠1=∠ADC,
∵∠2=∠3,
∴∠1=∠2,
即∠AGD=∠FGC;
练习2题解图
(2)解:如解图,∵∠FCG+∠DCG=180°,∠DCG+∠DAG=180°,
∴∠FCG=∠DAG,
∵∠1=∠2,
∴∠ADG=∠F,
∵∠ADG=∠ACG,
∴∠ACG=∠F,
∵∠CAG=∠CAF,
∴△CAG∽△FAC,
∴
∴AC2=AG·AF=192,
∴AC=8,
在Rt△ACE中,
∵∠AEC=90°,AC=8 ,CE=2 ,
∴AE=
易知△ACE∽△ABC,
∴
∴AC2=AE·AB,
∴AB=
∴⊙O的半径为
满分技法
1. 如图①,四边形ABCD是⊙O的内接四边形,AC、BD是⊙O的两条弦,根据同弧所对
的圆周角相等和对顶角相等可得到①△ABM∽△DCM;②△BCM∽△ADM,从而得到
(MA·MC=MB·MD).
2. 如图②,延长四边形ABCD的边BA、CD交于点P,根据圆内接四边形的性质∠PAD=∠BCD,∠PDA=∠ABC,可得到△PDA∽△PBC, ,而AD和BC分别在△ADM和△BCM中,且△ADM∽△BCM,从而得到更多的线段关系.
3. 如图③,当AC⊥BD时,恰好构成垂径定理的基本图形,适用于与其相关的所有结论.
