北师大版九年级数学下册2.2 二次函数的图象和性质 课件(共50张PPT)
文档属性
| 名称 | 北师大版九年级数学下册2.2 二次函数的图象和性质 课件(共50张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 09:01:44 | ||
图片预览










文档简介
第三单元 函数
第11讲 二次函数的图象与性质
(必考,1~2道,3~14分)
玩转贵阳10年中考真题
分式的相关概念(仅2019年考查)
命题点
1
1. (2015贵阳10题3分)已知二次函数y=-x2+2x+3,当x≥2时,y的取值范围是( )
A. y≥3 B. y≤3 C. y>3 D. y<3
2. (2012贵阳10题3分)已知二次函数y=ax2+bx+c(a<0)的图象如图所示,当-5≤x≤0时,下列说法正确的是( )
A. 有最小值-5、最大值0
B. 有最小值-3、最大值6
C. 有最小值0、最大值6
D. 有最小值2、最大值6
第2题图
B
B
3. (2011贵阳14题4分)写出一个开口向下的二次函数的表达式____________________.
4. (2013贵阳15题4分)已知二次函数y=x2+2mx+2,当x>2时,y的值随x值的增大而增大,则实数m的取值范围是____________.
y=-x2(答案不唯一)
m≥-2
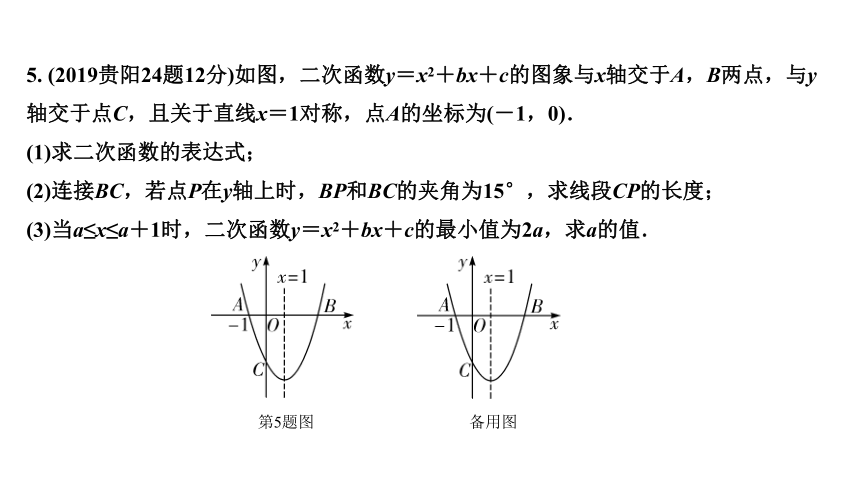
5. (2019贵阳24题12分)如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,且关于直线x=1对称,点A的坐标为(-1,0).
(1)求二次函数的表达式;
(2)连接BC,若点P在y轴上时,BP和BC的夹角为15°,求线段CP的长度;
(3)当a≤x≤a+1时,二次函数y=x2+bx+c的最小值为2a,求a的值.
第5题图
备用图
解:(1)∵A(-1,0),对称轴是直线x=1,∴B(3,0), 把A(-1,0),B(3,0)都代入y=x2+bx+c,得
,解得 , ∴二次函数的表达式为y=x2-2x-3; (2)∵y=x2-2x-3,∴C(0,-3),∴OB=OC=3, ∴∠OBC=∠OCB=45°, 如解图①,当点P在点C上方时,∠PBC=15°,则∠OBP=30°, ∴OP=OB·tan30°= ,此时CP=OC-OP=3- ; 如解图②,当点P在C点下方时,∠PBC=15°,则∠OBP=60°, ∴OP=OB·tan60°=3 ,此时CP=OP-OC=3 - 3. 综上,CP=3- 或3 -3;
第5题解图①
第5题解图②
(3)分三种情况:①当a+1<1(即a<0)时,y随x的增大而减小,当x=a+1时,y取最小值2a,即(a+1)2-2(a+1)-3=2a,
解得a1=1+ (舍去), a2=1- ;
当a≤1≤a+1,即0≤a≤1时,当x=1时,y有最小值为2a,
即1-2-3=2a,解得,a=-2(舍去);
当a>1时,y随x的增大而增大,当x=a时,y有最小值,
即a2-2a-3=2a,
解得a=2- (舍去)或a=2+ .
综上,a=1- 或2+ .
拓展训练
6. 若A(-4,y1),B(- ,y2),C(3,y3)为二次函数y=(x+2)2-9的图象上的三点,则y1,y2,y3的大小关系是( ) A. y1<y2<y3 B. y2<y1<y3 C. y3<y1<y2 D. y1<y3<y2 7. 二次函数y=x2-ax+b的图象如图所示,对称轴为直线x=2,下列结论不正确的是
( ) A. a=4 B. 当b=-6时,顶点的坐标为(2,-10) C. b>-5 D. 当x>3时,y随x的增大而增大
第7题图
B
C
8. (2019云南省卷)已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
(1)∵抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴, ∴x=- =0,即k2+k-6=0.解得k=-3或k=2. 当k=2时,二次函数解析式为y=x2+6,它的图象与x轴无交点,不满足题意,舍去. 当k=-3时,二次函数解析式为y=x2-9,它的图象与x轴有两个交点,满足题意. ∴k=-3; (2)由(1)知y=x2-9, ∵点P到y轴的距离为2, ∴点P的横坐标为-2或2. 当x=2时,y=-5; 当x=-2时,y=-5. ∴点P的坐标为(2,-5)或(-2,-5).
根据二次函数图象判断与系数有关的结论(2017.9单独考查,2015.24涉及)
命题点
2
9. (2017贵阳9题3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2-4ac>0;④- <0.正确的是( ) A. ①② B. ②④ C. ①③ D. ③④
第9题图
C
拓展训练
10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:①abc<0;②b2-4ac>0;③a+b+c>0;④a-b+c>0.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
第10题图
B
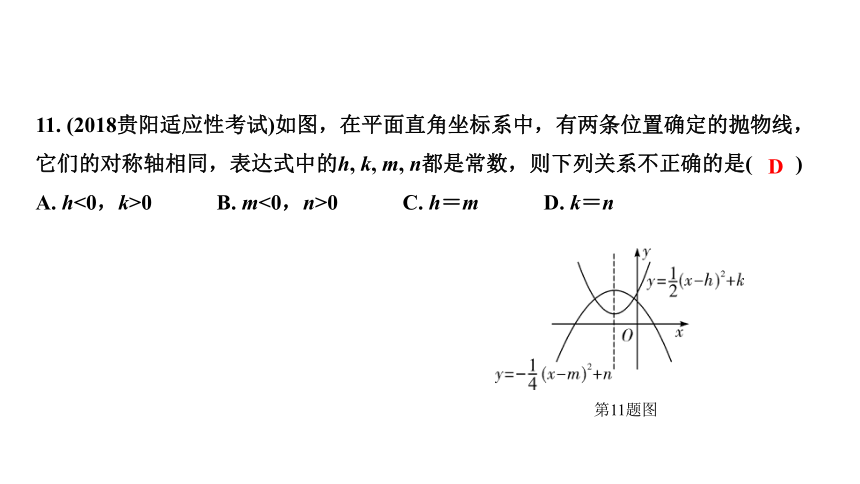
11. (2018贵阳适应性考试)如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,表达式中的h, k, m, n都是常数,则下列关系不正确的是( )
A. h<0,k>0 B. m<0,n>0 C. h=m D. k=n
第11题图
D
二次函数与方程、不等式的关系(10年4考)
命题点
3
12. (2016贵阳10题3分)若m,n(n<m)是关于x的一元二次方程1-(x-a)(x-b)=0的两个根,且b<a,则m,n,b,a的大小关系是( )
A. m<a<b<n B. a<m<n<b
C. b<n<m<a D. n<b<a<m
D
13. (2018贵阳10题3分)已知二次函数y=-x2+x+6及一次函数y=-x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=-x+m与新图象有4个交点时,m的取值范围是( )
A. -第13题图
D
14. (2013贵阳23题10分)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(1)顶点P的坐标是________;
(2)若直线y=ax+b经过另一点A(0,11),求出该直线的表达式;
(3)在(2)的条件下,若有一条直线y=mx+n与直线y=ax+b关于x轴成轴对称,求直线y=mx+n与抛物线y=-x2-2x+3的交点坐标.
第14题图
(-1,4)
解:(2)将P(-1,4)、A(0,11)代入y=ax+b中,可得
,解得 ,(5分) 故直线的表达式为y=7x+11;(6分) (3)∵y=mx+n与y=7x+11关于x轴对称, ∴直线y=mx+n的解析式为y=-(7x+11)=-7x-11,(7分) 由题意,将y=-7x-11与抛物线解析式联立,可得 , 解得 或 ,(9分) ∴交点坐标为(7,-60)和(-2,3).(10分)
拓展训练
15. 如图,在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于点A、B,若AB=4,则点M到直线l的距离为( )
A. 2 B. 3 C. 4 D. 5
16. 如图,将抛物线C:y=x2-6x+5在x轴下方的图象沿x轴翻折,翻折后得到的图象与抛物线C在x轴上方的图象记为G,已知直线l:y=x+m与图象G有两个公共点,则m的取值范围为( ) A. -5<m<-1 B. m> C. -5<m<-1或m> D. -5<m<
第15题图
第16题图
C
C
二次函数的图象与性质
二次函数与一元二次方程的关系
二次函数与不等式的关系
二次函数的图象与系数的关系
二次函数的性质
图象的平移
方法1:直接平移
方法2
考点精讲
二次函数的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}表达形式
一般式:
y=ax2+bx+c
顶点式:
y=a(x-h)2+k
交点式:
y=a(x-x1)(x-x2)
对称轴
________
x=h
x=
a的正负决定开口方向
a>0,开口向上;
a<0,开口向下
最值
a>0时,y有最小值
当x= 时,y的最值为
当x=h时,最值为k
当x= 时,y取得最值
a<0时,y有最大值
返回思维导图
(h,k)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}顶点坐标
__________
横坐标为x= ,纵坐标x= 时y的值
a>0
在对称轴左侧,y随x的增大而减小;在对称轴的右侧,y随x的增大而增大
a<0
在对称轴左侧,y随x的增大而增大;在对称轴的右侧,y随x的增大而减小
返回思维导图
二次函数的图象与系数的关系
y
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}a,b决定对称轴的位置
b=0
对称轴为______轴
a、b同号
对称轴在y轴左侧
a、b异号
对称轴在y轴右侧
c决定与y轴的交点
c=0
抛物线过原点
c>0
抛物线与y轴交于正半轴
c<0
抛物线与y轴交于负半轴
返回思维导图
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}b2-4ac决定与x轴交点个数
b2-4ac=0
与x轴有唯一的交点(顶点)
b2-4ac=0
b2-4ac>0
与x轴有两个交点
b2-4ac>0
b2-4ac<0
与x轴没有交点
b2-4ac<0
二次函数图象与a、b、c的关系
2a+b
与1比较
【易错提醒】在解题过程中,若不等号两边均有字母时,需将字母都移向不等号的一边,再进行比较
2a-b
与-1比较
a+b+c
令x=1,看纵坐标
a-b+c
令x=-1,看纵坐标
4a+2b+c
令x=2,看纵坐标
4a-2b+c
令x=-2,看纵坐标
返回思维导图
练一练 已知二次函数y=ax2+bx+c(a≠0),请用“>”、“<”或“=”判断下列各式与0的大小关系:
>
>
>
>
>
>
>
>
>
>
<
<
<
<
<
<
=
=
=
=
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(1) a____0;
b____0;
c____0;
b2-4ac____ 0;
a-b+c____0
(2) a____0;
b____0;
c____0;
b2-4ac____ 0;
2a-b____0
(3) a____0;
b____0;
c____0;
b2-4ac____ 0;
2a+b____0
(4) a____0;
b____0;
c____0;
b2-4ac____ 0;
a+b+c____0
返回思维导图
=
=
=
=
=
=
>
>
>
>
>
>
>
>
>
>
>
<
<
<
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(5) a____0;
b____0;
c____0;
b2-4ac____ 0;
4a+2b+c____0
(6) a____0;
b____0;
c____0;
b2-4ac____ 0;
a-b+c____0
(7) a____0;
b____0;
c____0;
b2-4ac____ 0;
2a+b____0
(8) a____0;
b____0;
c____0;
b2-4ac____ 0;
2a-b____0
返回思维导图
图象的平移
方法1:直接平移
1.把y=ax2+bx+c沿y轴向上(下)平移m(m>0)个单位得到
y=ax2+bx+c +m(或y=ax2+bx+c -m )
2. 把y=ax2+bx+c沿x轴向左(右)平移m(m>0)个单位得到
y=a(x +m )2+b(x +m )+c(或y=a(x -m )2+b(x -m )+c)
【满分技法】按平移规律“左加右减,上加下减”进行平移.左右平移时只变“x”,即只给x加减,切记给每一个“x”都要加减; 上下平移时,只变“c”值,即只给c值加减.
返回思维导图
图象的平移
方法2:可将二次函数解析式化为顶点式y=a(x-h)2+k
的形式,再按照下列方式变换:
【满分技法】二次函数图象的平移,其实质是图象上点的整体平移(一般研究顶点坐标),平移过程中a保持不变,因此可先求出顶点坐标,根据点的平移规律,得出平移后的顶点坐标,进而求得解析式.
返回思维导图
二次函数与一元二次方程关系
一元二次方程ax2+bx+c=0(a≠0)的解是二次函数y=ax2+bx+c的图象与x轴的交点的横坐标
方程有两个不相等的实数根?b2-4ac>0?二次函数与x轴有____个交点
方程有两个相等的实数根?b2-4ac=0?二次函数与x轴有____个交点
方程无实数根?b2-4ac<0?二次函数与x轴____交点
两
一
无
返回思维导图
二次函数与不等式的关系
函数y=ax2+bx+c的图象在x轴上方,函数图象上点的纵坐标都为正?不等式ax2+bx+c____0;
函数y=ax2+bx+c的图象在x轴下方,函数图象上点的纵坐标都为负?不等式ax2+bx+c_____0
>
<
返回思维导图
一、二次函数的图象与性质
y=(x-1)2-2
重难点突破
例1 已知抛物线y= x2-x- . (1)抛物线的开口方向为________; (2)化为顶点式的一般步骤: ①一化:________________,(将二次项系数化为1) ②二配:___________________,(将含有x的项配成完全平方式) ③三化:________________;(化为顶点式)
向上
y= (x2-2x)-
y= (x-1)2- -
y= (x-1)2-2
(3)抛物线的对称轴为直线________;
(4)抛物线的顶点坐标为________;
(5)抛物线与y轴的交点坐标是________,与x轴的交点坐标是__________________;
(6)当x________时,y随x的增大而增大;
(7)抛物线y有最______值(填“大”或“小”),值为________;
(8)若抛物线上有C(2,y1)、D(a,y2)两点,且a>2,则y1和y2的大小关系为________.
x=1
(1,-2)
(0,- )
≥1
小
(-1,0),(3,0)
-2
y2>y1
例2 已知二次函数y=x2-2x+2.
(1)在下面的直角坐标系中画出二次函数的图象;
例2题图
例2题解图
(1)画图如解图:
(2)根据(1)的图象填空: ①当-1≤x≤0时,二次函数的最大值是________,最小值是________; ②当-1≤x≤2时,二次函数的最大值是________,最小值是________; ③当0≤x≤3时,二次函数的最大值是________,最小值是________; (3)当a≤x≤3时, ①若二次函数的最小值是1,则a的取值范围是______; ②若二次函数的最小值为 ,则a的值是________; ③若二次函数的最大值为5,则a的取值范围是_________; ④若二次函数的最大值为10,则a的值是________;
5
2
5
1
5
1
a≤1
-1≤a<3
-2
(4)已知a≤x≤a+1, ①若x的取值范围在对称轴左侧,则a的取值范围是________,若此时的最小值为2,则a的值是______; ②若x的取值范围在对称轴右侧,则a的取值范围是________,若此时的最大值为5,则a的值是______; ③当x的取值范围包含二次函数的对称轴时,若x=a+1时取得最大值,此时a的取值范围是________,如此时的最大值是 ,则a的值是________,若x=a时取得最大值,此时a的取值范围________,若最大值为 ,则a的值是________.
a≤0
-1
a≥1
2
≤a≤1
0≤a≤
给定自变量取值范围的二次函数值的大小比较,其本质是比较自变量与对称轴的位置关系:
1. 当抛物线开口向上的时候,自变量到对称轴的距离越远,函数值越大,如图①;
2. 当抛物线开口向下的时候,自变量到对称轴的距离越远,函数值越小,如图②;
3. 若所给的自变量的取值范围含有参数,则在求最值的时候先要讨论抛物线的对称轴是否在自变量的取值范围内.
满分技法
图①
图②
二、二次函数解析式的确定
形式一 已知顶点坐标及a,b,c中的一个
练习1 已知抛物线y=x2 +bx+c的顶点坐标为(1,-3),求抛物线的解析式.
解:∵抛物线y=x2+bx+c的顶点坐标为(1,-3), ∴ ,解得 ,
∴抛物线的解析式为y=x2-2x-2.
形式二 已知顶点坐标和任意一点坐标
练习2 已知抛物线y=ax2+bx+c(a≠0)的图象以A(2,-3)为顶点,且过点B(4,-1),求抛物线的解析式.
解:∵抛物线y=ax2+bx+c(a≠0)的顶点坐标是(2,-3), ∴设抛物线的解析式为y=a(x-2)2-3, ∵抛物线经过点(4,-1), ∴a(4-2)2-3=-1, 解得a= , ∴抛物线的解析式为y= (x-2)2-3= x2-2x-1.
形式三 已知对称轴及x轴上一点与任意一点
练习3 对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴交于点A(3,0),且经过点B(4,-3),求抛物线的解析式.
解:∵抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=2,且与x轴交于点A(3,0),
∴抛物线与x轴的另一个交点为(1,0),
∴设抛物线的解析式为y=a(x-1)(x-3),
又∵抛物线经过点(4,-3),
∴将点(4,-3)代入解析式得:-3=a(4-1)(4-3),解得a=-1,
∴抛物线的解析式为y=-(x-1)(x-3)=-x2+4x-3.
练习4 在平面直角坐标系中,抛物线y=ax2-2ax+c(a≠0)与x轴交于点A(3,0),且经过点B(2,3),求抛物线的解析式.
解:由题意得,抛物线的对称轴为直线x=- =1, ∵抛物线与x轴交于点A(3,0), ∴抛物线与 x 轴的另一个交点为(-1,0), ∴ 设抛物线的解析式为y=a(x +1)(x-3), 又∵抛物线经过点(2,3), ∴将点(2,3)代入解析式得:3=a(2+1)(2-3),解得a=-1, ∴抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3.
形式四 已知两点坐标及a,b,c中的一个
练习5 已知抛物线y=-3x2 +bx+c经过点A(1,7)和点B(2,4),求抛物线的解析式.
解:∵抛物线y=-3x2 +bx+c经过点A(1,7)和点B(2,4), ∴将点A(1,7)和点B(2,4)代入y=-3x2+bx+c中,得
,解得 , ∴抛物线的解析式为y=-3x2 +6x+4.
解:将点(0,-6),点(2,-4)和点(3,0)代入y=ax2 +bx+c中,得
,解得 ,
∴抛物线的解析式为y=x2-x-6.
形式五 已知任意三点坐标
练习6 已知抛物线y=ax2 +bx+c(a≠0)经过点(0,-6),点(2,-4)和
点(3,0),求抛物线的解析式.
形式六 二次函数图象的平移
练习7 将抛物线y= (x-2)2+2先向左平移3个单位长度,再向下平移4个单位长度,求新的抛物线的解析式.
解:将抛物线y= (x-2)2+2向左平移3个单位,得到的抛物线为y= (x-2+3)2+2= (x+1)2+2,再向下平移4个单位后,得到的抛物线为:y= (x+1)2+2-4,即y= (x+1)2-2.
三、在坐标系中求动点所在的函数图象解析式
已知平面直角坐标系中一点A(m,m2-2m),其中m为任意实数.
(1)当m=0时,点A的坐标是________;当m=1时,点A的坐标是________;
(2)当m=x时,点A的横坐标是x;点A的纵坐标y是________;即y与x的关系式是______________;所以点A在二次函数______________的图象上
(0,0)
(1,-1)
x2-2x
y= x2-2x
y=x2-2x
热身小练习
练习8 如图,点M(x,y)为平面直角坐标系中第一象限内一点,过点M作MA⊥x轴于点A, MB⊥y轴于点B,若四边形MBOA是正方形,则y关于x的函数关系式为________,自变量x的取值范围是________.
练习8题图
y=x
x>0
练习9 如图,点A在x轴上,OA=1,B为y轴正半轴上的动点,以点A,B为直角边,在第一象限作等腰直角三角形ABM,使点B为直角顶点,求点M所在的函数图象的解析式
练习9题图
解:设OB=m,如解图,过点M作MC⊥y轴于点C,
∵△ABM是等腰直角三角形,点B是直角顶点,
∴BM=BA,∠MBC+∠OBA=90°,
∵∠MBC+∠CMB=90°,
∴∠CMB=∠OBA,
∴Rt△BMC≌Rt△ABO,
∴MC=OB=m,BC=OA=1,
∴点M(m,m+1),
即x=m,y=m+1,
∴点M所在的函数图象的解析式为y=x+1.
练习9题解图
练习10 如图,平面直角坐标系中,直线l经过点(0,-1)且平行于x轴,已知点B(0,1),M(x,y)为平面直角坐标系中的动点,过点M作MA⊥l于点A,若MB=MA,求点M所在的函数图象的解析式.
练习10题图
解:∵B(0,1),M(x,y), ∴MB2=x2+(y-1)2, ∵MA⊥l, ∴MA=y+1, ∵MB=MA, ∴x2+(y-1)2=(y+1)2, 整理得y= x2. ∴点M所在的函数图象的解析式为y= x2.
四、二次函数与方程、不等式的关系
例3 如图,直线l的解析式为y=- x+1,已知抛物线y=ax2+2x+2; (1)若抛物线与l有两个交点,则a的取值范围是______________; (2)A(-3,2),B(3,0)为l上两点.若抛物线与线段AB有两个交点,首先要满足(1)中的条件即:___________; ①当抛物线开口方向向上时,即a>0,如图①所示,当x=-3时,- x+1________ax2+2x+2;当x=3时,- x+1________ax2+2x+2.(填“>” “=”或“<”).所以此时a的取值范围是__________.
例3题图①
<
<
a< 且a≠0
a< 且a≠0
<a<
②当抛物线开口方向向下时,即a<0,如图②所示,当x=-3时,- x+1________ax2+2x+2;当x=3时,- x+1________ax2+2x+2.(填“>” “=”或“<”).所以此时a的取值范围是________. 综上,当y=ax2+2x+2与线段AB有两个交点时,a的取值范围是___________________.
例3题图②
>
>
a<-
a<- 或 <a<
练习11 (2018兰州)如图,抛物线y= x2-7x+ 与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向左平移得C2,C2与x轴交于点B,D,若直线y=
x+m与C1、C2共有3个不同的交点,则m的取值范围是( ) A. - <m<- B. - <m<- C. - <m<- D. - <m<-
练习11题图
C
第11讲 二次函数的图象与性质
(必考,1~2道,3~14分)
玩转贵阳10年中考真题
分式的相关概念(仅2019年考查)
命题点
1
1. (2015贵阳10题3分)已知二次函数y=-x2+2x+3,当x≥2时,y的取值范围是( )
A. y≥3 B. y≤3 C. y>3 D. y<3
2. (2012贵阳10题3分)已知二次函数y=ax2+bx+c(a<0)的图象如图所示,当-5≤x≤0时,下列说法正确的是( )
A. 有最小值-5、最大值0
B. 有最小值-3、最大值6
C. 有最小值0、最大值6
D. 有最小值2、最大值6
第2题图
B
B
3. (2011贵阳14题4分)写出一个开口向下的二次函数的表达式____________________.
4. (2013贵阳15题4分)已知二次函数y=x2+2mx+2,当x>2时,y的值随x值的增大而增大,则实数m的取值范围是____________.
y=-x2(答案不唯一)
m≥-2
5. (2019贵阳24题12分)如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,且关于直线x=1对称,点A的坐标为(-1,0).
(1)求二次函数的表达式;
(2)连接BC,若点P在y轴上时,BP和BC的夹角为15°,求线段CP的长度;
(3)当a≤x≤a+1时,二次函数y=x2+bx+c的最小值为2a,求a的值.
第5题图
备用图
解:(1)∵A(-1,0),对称轴是直线x=1,∴B(3,0), 把A(-1,0),B(3,0)都代入y=x2+bx+c,得
,解得 , ∴二次函数的表达式为y=x2-2x-3; (2)∵y=x2-2x-3,∴C(0,-3),∴OB=OC=3, ∴∠OBC=∠OCB=45°, 如解图①,当点P在点C上方时,∠PBC=15°,则∠OBP=30°, ∴OP=OB·tan30°= ,此时CP=OC-OP=3- ; 如解图②,当点P在C点下方时,∠PBC=15°,则∠OBP=60°, ∴OP=OB·tan60°=3 ,此时CP=OP-OC=3 - 3. 综上,CP=3- 或3 -3;
第5题解图①
第5题解图②
(3)分三种情况:①当a+1<1(即a<0)时,y随x的增大而减小,当x=a+1时,y取最小值2a,即(a+1)2-2(a+1)-3=2a,
解得a1=1+ (舍去), a2=1- ;
当a≤1≤a+1,即0≤a≤1时,当x=1时,y有最小值为2a,
即1-2-3=2a,解得,a=-2(舍去);
当a>1时,y随x的增大而增大,当x=a时,y有最小值,
即a2-2a-3=2a,
解得a=2- (舍去)或a=2+ .
综上,a=1- 或2+ .
拓展训练
6. 若A(-4,y1),B(- ,y2),C(3,y3)为二次函数y=(x+2)2-9的图象上的三点,则y1,y2,y3的大小关系是( ) A. y1<y2<y3 B. y2<y1<y3 C. y3<y1<y2 D. y1<y3<y2 7. 二次函数y=x2-ax+b的图象如图所示,对称轴为直线x=2,下列结论不正确的是
( ) A. a=4 B. 当b=-6时,顶点的坐标为(2,-10) C. b>-5 D. 当x>3时,y随x的增大而增大
第7题图
B
C
8. (2019云南省卷)已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
(1)∵抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴, ∴x=- =0,即k2+k-6=0.解得k=-3或k=2. 当k=2时,二次函数解析式为y=x2+6,它的图象与x轴无交点,不满足题意,舍去. 当k=-3时,二次函数解析式为y=x2-9,它的图象与x轴有两个交点,满足题意. ∴k=-3; (2)由(1)知y=x2-9, ∵点P到y轴的距离为2, ∴点P的横坐标为-2或2. 当x=2时,y=-5; 当x=-2时,y=-5. ∴点P的坐标为(2,-5)或(-2,-5).
根据二次函数图象判断与系数有关的结论(2017.9单独考查,2015.24涉及)
命题点
2
9. (2017贵阳9题3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2-4ac>0;④- <0.正确的是( ) A. ①② B. ②④ C. ①③ D. ③④
第9题图
C
拓展训练
10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:①abc<0;②b2-4ac>0;③a+b+c>0;④a-b+c>0.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
第10题图
B
11. (2018贵阳适应性考试)如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,表达式中的h, k, m, n都是常数,则下列关系不正确的是( )
A. h<0,k>0 B. m<0,n>0 C. h=m D. k=n
第11题图
D
二次函数与方程、不等式的关系(10年4考)
命题点
3
12. (2016贵阳10题3分)若m,n(n<m)是关于x的一元二次方程1-(x-a)(x-b)=0的两个根,且b<a,则m,n,b,a的大小关系是( )
A. m<a<b<n B. a<m<n<b
C. b<n<m<a D. n<b<a<m
D
13. (2018贵阳10题3分)已知二次函数y=-x2+x+6及一次函数y=-x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=-x+m与新图象有4个交点时,m的取值范围是( )
A. -
D
14. (2013贵阳23题10分)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(1)顶点P的坐标是________;
(2)若直线y=ax+b经过另一点A(0,11),求出该直线的表达式;
(3)在(2)的条件下,若有一条直线y=mx+n与直线y=ax+b关于x轴成轴对称,求直线y=mx+n与抛物线y=-x2-2x+3的交点坐标.
第14题图
(-1,4)
解:(2)将P(-1,4)、A(0,11)代入y=ax+b中,可得
,解得 ,(5分) 故直线的表达式为y=7x+11;(6分) (3)∵y=mx+n与y=7x+11关于x轴对称, ∴直线y=mx+n的解析式为y=-(7x+11)=-7x-11,(7分) 由题意,将y=-7x-11与抛物线解析式联立,可得 , 解得 或 ,(9分) ∴交点坐标为(7,-60)和(-2,3).(10分)
拓展训练
15. 如图,在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于点A、B,若AB=4,则点M到直线l的距离为( )
A. 2 B. 3 C. 4 D. 5
16. 如图,将抛物线C:y=x2-6x+5在x轴下方的图象沿x轴翻折,翻折后得到的图象与抛物线C在x轴上方的图象记为G,已知直线l:y=x+m与图象G有两个公共点,则m的取值范围为( ) A. -5<m<-1 B. m> C. -5<m<-1或m> D. -5<m<
第15题图
第16题图
C
C
二次函数的图象与性质
二次函数与一元二次方程的关系
二次函数与不等式的关系
二次函数的图象与系数的关系
二次函数的性质
图象的平移
方法1:直接平移
方法2
考点精讲
二次函数的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}表达形式
一般式:
y=ax2+bx+c
顶点式:
y=a(x-h)2+k
交点式:
y=a(x-x1)(x-x2)
对称轴
________
x=h
x=
a的正负决定开口方向
a>0,开口向上;
a<0,开口向下
最值
a>0时,y有最小值
当x= 时,y的最值为
当x=h时,最值为k
当x= 时,y取得最值
a<0时,y有最大值
返回思维导图
(h,k)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}顶点坐标
__________
横坐标为x= ,纵坐标x= 时y的值
a>0
在对称轴左侧,y随x的增大而减小;在对称轴的右侧,y随x的增大而增大
a<0
在对称轴左侧,y随x的增大而增大;在对称轴的右侧,y随x的增大而减小
返回思维导图
二次函数的图象与系数的关系
y
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}a,b决定对称轴的位置
b=0
对称轴为______轴
a、b同号
对称轴在y轴左侧
a、b异号
对称轴在y轴右侧
c决定与y轴的交点
c=0
抛物线过原点
c>0
抛物线与y轴交于正半轴
c<0
抛物线与y轴交于负半轴
返回思维导图
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}b2-4ac决定与x轴交点个数
b2-4ac=0
与x轴有唯一的交点(顶点)
b2-4ac=0
b2-4ac>0
与x轴有两个交点
b2-4ac>0
b2-4ac<0
与x轴没有交点
b2-4ac<0
二次函数图象与a、b、c的关系
2a+b
与1比较
【易错提醒】在解题过程中,若不等号两边均有字母时,需将字母都移向不等号的一边,再进行比较
2a-b
与-1比较
a+b+c
令x=1,看纵坐标
a-b+c
令x=-1,看纵坐标
4a+2b+c
令x=2,看纵坐标
4a-2b+c
令x=-2,看纵坐标
返回思维导图
练一练 已知二次函数y=ax2+bx+c(a≠0),请用“>”、“<”或“=”判断下列各式与0的大小关系:
>
>
>
>
>
>
>
>
>
>
<
<
<
<
<
<
=
=
=
=
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(1) a____0;
b____0;
c____0;
b2-4ac____ 0;
a-b+c____0
(2) a____0;
b____0;
c____0;
b2-4ac____ 0;
2a-b____0
(3) a____0;
b____0;
c____0;
b2-4ac____ 0;
2a+b____0
(4) a____0;
b____0;
c____0;
b2-4ac____ 0;
a+b+c____0
返回思维导图
=
=
=
=
=
=
>
>
>
>
>
>
>
>
>
>
>
<
<
<
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(5) a____0;
b____0;
c____0;
b2-4ac____ 0;
4a+2b+c____0
(6) a____0;
b____0;
c____0;
b2-4ac____ 0;
a-b+c____0
(7) a____0;
b____0;
c____0;
b2-4ac____ 0;
2a+b____0
(8) a____0;
b____0;
c____0;
b2-4ac____ 0;
2a-b____0
返回思维导图
图象的平移
方法1:直接平移
1.把y=ax2+bx+c沿y轴向上(下)平移m(m>0)个单位得到
y=ax2+bx+c +m(或y=ax2+bx+c -m )
2. 把y=ax2+bx+c沿x轴向左(右)平移m(m>0)个单位得到
y=a(x +m )2+b(x +m )+c(或y=a(x -m )2+b(x -m )+c)
【满分技法】按平移规律“左加右减,上加下减”进行平移.左右平移时只变“x”,即只给x加减,切记给每一个“x”都要加减; 上下平移时,只变“c”值,即只给c值加减.
返回思维导图
图象的平移
方法2:可将二次函数解析式化为顶点式y=a(x-h)2+k
的形式,再按照下列方式变换:
【满分技法】二次函数图象的平移,其实质是图象上点的整体平移(一般研究顶点坐标),平移过程中a保持不变,因此可先求出顶点坐标,根据点的平移规律,得出平移后的顶点坐标,进而求得解析式.
返回思维导图
二次函数与一元二次方程关系
一元二次方程ax2+bx+c=0(a≠0)的解是二次函数y=ax2+bx+c的图象与x轴的交点的横坐标
方程有两个不相等的实数根?b2-4ac>0?二次函数与x轴有____个交点
方程有两个相等的实数根?b2-4ac=0?二次函数与x轴有____个交点
方程无实数根?b2-4ac<0?二次函数与x轴____交点
两
一
无
返回思维导图
二次函数与不等式的关系
函数y=ax2+bx+c的图象在x轴上方,函数图象上点的纵坐标都为正?不等式ax2+bx+c____0;
函数y=ax2+bx+c的图象在x轴下方,函数图象上点的纵坐标都为负?不等式ax2+bx+c_____0
>
<
返回思维导图
一、二次函数的图象与性质
y=(x-1)2-2
重难点突破
例1 已知抛物线y= x2-x- . (1)抛物线的开口方向为________; (2)化为顶点式的一般步骤: ①一化:________________,(将二次项系数化为1) ②二配:___________________,(将含有x的项配成完全平方式) ③三化:________________;(化为顶点式)
向上
y= (x2-2x)-
y= (x-1)2- -
y= (x-1)2-2
(3)抛物线的对称轴为直线________;
(4)抛物线的顶点坐标为________;
(5)抛物线与y轴的交点坐标是________,与x轴的交点坐标是__________________;
(6)当x________时,y随x的增大而增大;
(7)抛物线y有最______值(填“大”或“小”),值为________;
(8)若抛物线上有C(2,y1)、D(a,y2)两点,且a>2,则y1和y2的大小关系为________.
x=1
(1,-2)
(0,- )
≥1
小
(-1,0),(3,0)
-2
y2>y1
例2 已知二次函数y=x2-2x+2.
(1)在下面的直角坐标系中画出二次函数的图象;
例2题图
例2题解图
(1)画图如解图:
(2)根据(1)的图象填空: ①当-1≤x≤0时,二次函数的最大值是________,最小值是________; ②当-1≤x≤2时,二次函数的最大值是________,最小值是________; ③当0≤x≤3时,二次函数的最大值是________,最小值是________; (3)当a≤x≤3时, ①若二次函数的最小值是1,则a的取值范围是______; ②若二次函数的最小值为 ,则a的值是________; ③若二次函数的最大值为5,则a的取值范围是_________; ④若二次函数的最大值为10,则a的值是________;
5
2
5
1
5
1
a≤1
-1≤a<3
-2
(4)已知a≤x≤a+1, ①若x的取值范围在对称轴左侧,则a的取值范围是________,若此时的最小值为2,则a的值是______; ②若x的取值范围在对称轴右侧,则a的取值范围是________,若此时的最大值为5,则a的值是______; ③当x的取值范围包含二次函数的对称轴时,若x=a+1时取得最大值,此时a的取值范围是________,如此时的最大值是 ,则a的值是________,若x=a时取得最大值,此时a的取值范围________,若最大值为 ,则a的值是________.
a≤0
-1
a≥1
2
≤a≤1
0≤a≤
给定自变量取值范围的二次函数值的大小比较,其本质是比较自变量与对称轴的位置关系:
1. 当抛物线开口向上的时候,自变量到对称轴的距离越远,函数值越大,如图①;
2. 当抛物线开口向下的时候,自变量到对称轴的距离越远,函数值越小,如图②;
3. 若所给的自变量的取值范围含有参数,则在求最值的时候先要讨论抛物线的对称轴是否在自变量的取值范围内.
满分技法
图①
图②
二、二次函数解析式的确定
形式一 已知顶点坐标及a,b,c中的一个
练习1 已知抛物线y=x2 +bx+c的顶点坐标为(1,-3),求抛物线的解析式.
解:∵抛物线y=x2+bx+c的顶点坐标为(1,-3), ∴ ,解得 ,
∴抛物线的解析式为y=x2-2x-2.
形式二 已知顶点坐标和任意一点坐标
练习2 已知抛物线y=ax2+bx+c(a≠0)的图象以A(2,-3)为顶点,且过点B(4,-1),求抛物线的解析式.
解:∵抛物线y=ax2+bx+c(a≠0)的顶点坐标是(2,-3), ∴设抛物线的解析式为y=a(x-2)2-3, ∵抛物线经过点(4,-1), ∴a(4-2)2-3=-1, 解得a= , ∴抛物线的解析式为y= (x-2)2-3= x2-2x-1.
形式三 已知对称轴及x轴上一点与任意一点
练习3 对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴交于点A(3,0),且经过点B(4,-3),求抛物线的解析式.
解:∵抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=2,且与x轴交于点A(3,0),
∴抛物线与x轴的另一个交点为(1,0),
∴设抛物线的解析式为y=a(x-1)(x-3),
又∵抛物线经过点(4,-3),
∴将点(4,-3)代入解析式得:-3=a(4-1)(4-3),解得a=-1,
∴抛物线的解析式为y=-(x-1)(x-3)=-x2+4x-3.
练习4 在平面直角坐标系中,抛物线y=ax2-2ax+c(a≠0)与x轴交于点A(3,0),且经过点B(2,3),求抛物线的解析式.
解:由题意得,抛物线的对称轴为直线x=- =1, ∵抛物线与x轴交于点A(3,0), ∴抛物线与 x 轴的另一个交点为(-1,0), ∴ 设抛物线的解析式为y=a(x +1)(x-3), 又∵抛物线经过点(2,3), ∴将点(2,3)代入解析式得:3=a(2+1)(2-3),解得a=-1, ∴抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3.
形式四 已知两点坐标及a,b,c中的一个
练习5 已知抛物线y=-3x2 +bx+c经过点A(1,7)和点B(2,4),求抛物线的解析式.
解:∵抛物线y=-3x2 +bx+c经过点A(1,7)和点B(2,4), ∴将点A(1,7)和点B(2,4)代入y=-3x2+bx+c中,得
,解得 , ∴抛物线的解析式为y=-3x2 +6x+4.
解:将点(0,-6),点(2,-4)和点(3,0)代入y=ax2 +bx+c中,得
,解得 ,
∴抛物线的解析式为y=x2-x-6.
形式五 已知任意三点坐标
练习6 已知抛物线y=ax2 +bx+c(a≠0)经过点(0,-6),点(2,-4)和
点(3,0),求抛物线的解析式.
形式六 二次函数图象的平移
练习7 将抛物线y= (x-2)2+2先向左平移3个单位长度,再向下平移4个单位长度,求新的抛物线的解析式.
解:将抛物线y= (x-2)2+2向左平移3个单位,得到的抛物线为y= (x-2+3)2+2= (x+1)2+2,再向下平移4个单位后,得到的抛物线为:y= (x+1)2+2-4,即y= (x+1)2-2.
三、在坐标系中求动点所在的函数图象解析式
已知平面直角坐标系中一点A(m,m2-2m),其中m为任意实数.
(1)当m=0时,点A的坐标是________;当m=1时,点A的坐标是________;
(2)当m=x时,点A的横坐标是x;点A的纵坐标y是________;即y与x的关系式是______________;所以点A在二次函数______________的图象上
(0,0)
(1,-1)
x2-2x
y= x2-2x
y=x2-2x
热身小练习
练习8 如图,点M(x,y)为平面直角坐标系中第一象限内一点,过点M作MA⊥x轴于点A, MB⊥y轴于点B,若四边形MBOA是正方形,则y关于x的函数关系式为________,自变量x的取值范围是________.
练习8题图
y=x
x>0
练习9 如图,点A在x轴上,OA=1,B为y轴正半轴上的动点,以点A,B为直角边,在第一象限作等腰直角三角形ABM,使点B为直角顶点,求点M所在的函数图象的解析式
练习9题图
解:设OB=m,如解图,过点M作MC⊥y轴于点C,
∵△ABM是等腰直角三角形,点B是直角顶点,
∴BM=BA,∠MBC+∠OBA=90°,
∵∠MBC+∠CMB=90°,
∴∠CMB=∠OBA,
∴Rt△BMC≌Rt△ABO,
∴MC=OB=m,BC=OA=1,
∴点M(m,m+1),
即x=m,y=m+1,
∴点M所在的函数图象的解析式为y=x+1.
练习9题解图
练习10 如图,平面直角坐标系中,直线l经过点(0,-1)且平行于x轴,已知点B(0,1),M(x,y)为平面直角坐标系中的动点,过点M作MA⊥l于点A,若MB=MA,求点M所在的函数图象的解析式.
练习10题图
解:∵B(0,1),M(x,y), ∴MB2=x2+(y-1)2, ∵MA⊥l, ∴MA=y+1, ∵MB=MA, ∴x2+(y-1)2=(y+1)2, 整理得y= x2. ∴点M所在的函数图象的解析式为y= x2.
四、二次函数与方程、不等式的关系
例3 如图,直线l的解析式为y=- x+1,已知抛物线y=ax2+2x+2; (1)若抛物线与l有两个交点,则a的取值范围是______________; (2)A(-3,2),B(3,0)为l上两点.若抛物线与线段AB有两个交点,首先要满足(1)中的条件即:___________; ①当抛物线开口方向向上时,即a>0,如图①所示,当x=-3时,- x+1________ax2+2x+2;当x=3时,- x+1________ax2+2x+2.(填“>” “=”或“<”).所以此时a的取值范围是__________.
例3题图①
<
<
a< 且a≠0
a< 且a≠0
<a<
②当抛物线开口方向向下时,即a<0,如图②所示,当x=-3时,- x+1________ax2+2x+2;当x=3时,- x+1________ax2+2x+2.(填“>” “=”或“<”).所以此时a的取值范围是________. 综上,当y=ax2+2x+2与线段AB有两个交点时,a的取值范围是___________________.
例3题图②
>
>
a<-
a<- 或 <a<
练习11 (2018兰州)如图,抛物线y= x2-7x+ 与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向左平移得C2,C2与x轴交于点B,D,若直线y=
x+m与C1、C2共有3个不同的交点,则m的取值范围是( ) A. - <m<- B. - <m<- C. - <m<- D. - <m<-
练习11题图
C
