高二数学人教B版(2019)选择性必修第二册第三章3.3二项式定理与杨辉三角课件(共16张PPT)
文档属性
| 名称 | 高二数学人教B版(2019)选择性必修第二册第三章3.3二项式定理与杨辉三角课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 422.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 22:22:54 | ||
图片预览





文档简介
二项式定理与杨辉三角
主讲人:
时间:2021年1月5日
学习目标
1、掌握二项式定理及二项展开式的通项公式,熟练地进
行二项式的展开及求解某些指定的项;
2、熟练掌握赋值法的应用,领会函数方程思想和转化化
归思想;能够求展开式中系数的最大值,培养数学运
算的核心素养。
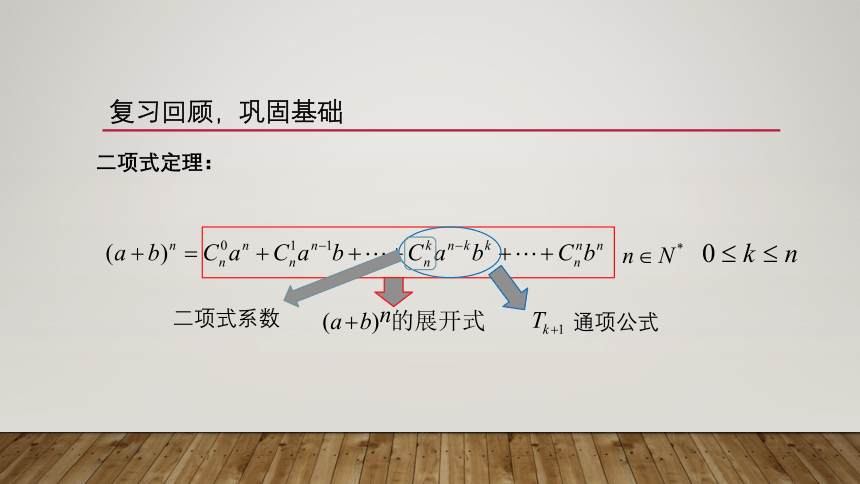
复习回顾,巩固基础
二项式定理:
通项公式
二项式系数
复习回顾,巩固基础
令
令
所有二项式系数之和为
奇数项和偶数项的二项式系数和相同
复习回顾,巩固基础
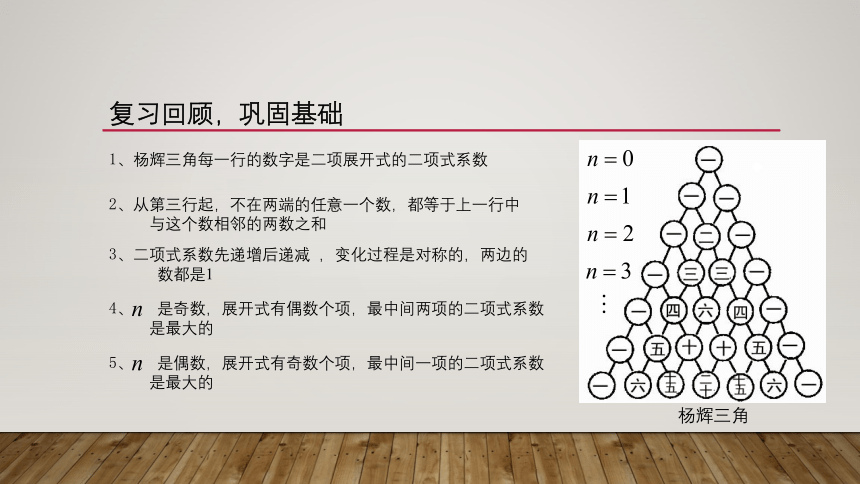
1、杨辉三角每一行的数字是二项展开式的二项式系数
2、从第三行起,不在两端的任意一个数,都等于上一行中
与这个数相邻的两数之和
4、 是奇数,展开式有偶数个项,最中间两项的二项式系数
是最大的
5、 是偶数,展开式有奇数个项,最中间一项的二项式系数
是最大的
杨辉三角
3、二项式系数先递增后递减 ,变化过程是对称的,两边的
数都是1
题型一:求特定项的系数
解:
令
解得
得
于是 的系数为
例题1、求 的展开式中 的系数
题型一:求特定项的系数
变式1-1、求 的展开式中 的系数
解:
的通项公式为
其中 的系数为
其中 的系数为
所以 的展开式中 的系数为
题型一:求特定项系数
变式1-2、求 的展开式中 的系数
答案:-11
解:
题型一:求特定项系数
总结:1、通过二项展开式的通项公式求解
2、通过二项式定理的证明方法求解
题型二:赋值法的应用
例题2:已知 。求
令
解:
(1)
(2)
(3)
(4)
函数方程思想的体现
题型二:赋值法的应用
变式2-1: ,求 的值。
解:令 得
的通项公式为
且
令 原式变为
于是
换元法 转化与化归思想
题型二:赋值法的应用
变式2-1: ,求 的值。
是新的二项展开式中 的系数
由此可知,
令 原式变为
解:
题型三:最大系数问题
例题3:已知 的展开式中各项系数和比各项的二项式系数和大 .
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项。
解:(1)
即
是奇数,因此二项式系数最大的项是第3,4项,分别是
题型三:最大系数问题
例题3:已知 的展开式中各项系数和比各项的二项式系数和大 .
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项。
解得
因为 ,可得
故系数最大的项是
解:(2)设第 项的系数最大,则有
课堂回顾
一、求展开式中的特定项的系数
二、赋值法的应用
三、最大系数问题
题型方法总结
思想方法总结
一、函数与方程思想
二、转化与化归思想
课后作业
1、完成导学案课后例题
2、整理笔记
主讲人:
时间:2021年1月5日
学习目标
1、掌握二项式定理及二项展开式的通项公式,熟练地进
行二项式的展开及求解某些指定的项;
2、熟练掌握赋值法的应用,领会函数方程思想和转化化
归思想;能够求展开式中系数的最大值,培养数学运
算的核心素养。
复习回顾,巩固基础
二项式定理:
通项公式
二项式系数
复习回顾,巩固基础
令
令
所有二项式系数之和为
奇数项和偶数项的二项式系数和相同
复习回顾,巩固基础
1、杨辉三角每一行的数字是二项展开式的二项式系数
2、从第三行起,不在两端的任意一个数,都等于上一行中
与这个数相邻的两数之和
4、 是奇数,展开式有偶数个项,最中间两项的二项式系数
是最大的
5、 是偶数,展开式有奇数个项,最中间一项的二项式系数
是最大的
杨辉三角
3、二项式系数先递增后递减 ,变化过程是对称的,两边的
数都是1
题型一:求特定项的系数
解:
令
解得
得
于是 的系数为
例题1、求 的展开式中 的系数
题型一:求特定项的系数
变式1-1、求 的展开式中 的系数
解:
的通项公式为
其中 的系数为
其中 的系数为
所以 的展开式中 的系数为
题型一:求特定项系数
变式1-2、求 的展开式中 的系数
答案:-11
解:
题型一:求特定项系数
总结:1、通过二项展开式的通项公式求解
2、通过二项式定理的证明方法求解
题型二:赋值法的应用
例题2:已知 。求
令
解:
(1)
(2)
(3)
(4)
函数方程思想的体现
题型二:赋值法的应用
变式2-1: ,求 的值。
解:令 得
的通项公式为
且
令 原式变为
于是
换元法 转化与化归思想
题型二:赋值法的应用
变式2-1: ,求 的值。
是新的二项展开式中 的系数
由此可知,
令 原式变为
解:
题型三:最大系数问题
例题3:已知 的展开式中各项系数和比各项的二项式系数和大 .
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项。
解:(1)
即
是奇数,因此二项式系数最大的项是第3,4项,分别是
题型三:最大系数问题
例题3:已知 的展开式中各项系数和比各项的二项式系数和大 .
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项。
解得
因为 ,可得
故系数最大的项是
解:(2)设第 项的系数最大,则有
课堂回顾
一、求展开式中的特定项的系数
二、赋值法的应用
三、最大系数问题
题型方法总结
思想方法总结
一、函数与方程思想
二、转化与化归思想
课后作业
1、完成导学案课后例题
2、整理笔记
同课章节目录
