北师大版九年级数学下册 第二章 2.2二次函数的图象与性质(4) 课件(共19张PPT)
文档属性
| 名称 | 北师大版九年级数学下册 第二章 2.2二次函数的图象与性质(4) 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 22:48:37 | ||
图片预览






文档简介
二次函数的一般形式是:
y=ax2+bx+c (a ≠ 0)
二次函数的顶点式是:
y=a(x-h)2+k (a ≠ 0)
二次函数y=a(x-h)2+k的性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
(h,k)
(h,k)
直线x=h
向上
向下
当x=h时,y有最小值为k.
当x=h时, y有最大值为k.
当x当x>h时, y随着x的增大而增大.
根据图象填表:
直线x=h
当x当x>h时, y随着x的增大而减小.
y=a(x-h)2+k(a<0)
y=a(x-h)2+k(a>0)
0
1
2
3
4
5
x
-1
-2
-3
-4
1
2
4
6
8
10
y
2.二次函数 y=2(x+3)2 -5
图象开口 ,对称轴是 ,顶点坐标是 ,当x= 时,y有最 值是 。
向上
直线x=-3
(-3,-5)
-3
小
-5
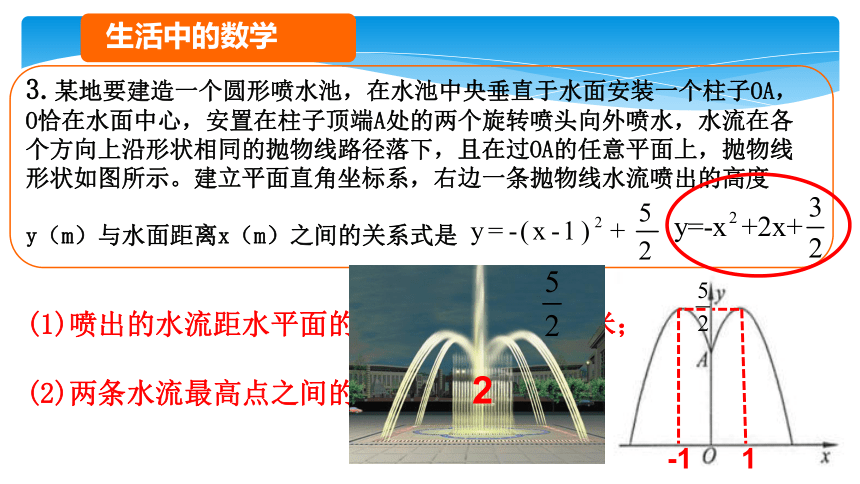
3.某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个柱子OA,
O恰在水面中心,安置在柱子顶端A处的两个旋转喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任意平面上,抛物线形状如图所示。建立平面直角坐标系,右边一条抛物线水流喷出的高度
y(m)与水面距离x(m)之间的关系式是
(1)喷出的水流距水平面的最大高度是 米;
(2)两条水流最高点之间的距离是 米。
1
2
-1
生活中的数学
y=2x2-8x+7
y=a(x-h)2+k
转化
?
用配方法求二次函数y=2x2-8x+7图象的
对称轴和顶点坐标。
2.用配方法将二次函数由一般式转化为顶点式的步骤:
①提二次项系数;
1.选择最优的解题方法
题后反思:
②配方;
③化简
用配方法确定下列二次函数图象的对称轴
和顶点坐标。
(1) y=3x2-6x+7 (2) y=-2x2-12x+8
求二次函数y=ax?+bx+c图象的对称轴和顶点坐标.
顶点式
y=a(x-h)2 +k
二次函数y=ax2+bx+c (a ≠ 0)的图象是一条抛物线
用公式法求二次函数y=2x2-8x+7图象的
对称轴和顶点坐标。
根据公式法确定下列二次函数图象的对称轴和顶点坐标。
y=2x2-4x-1
如图,桥梁的两条钢缆具有相同的抛物线形状,而且左、右两条抛物线关于y轴对称。按照图中的直角坐标系,左面的一条抛物线可以用
表示.
(1)钢缆的最低点到桥面的距离是多少?
(2)两条钢缆最低点之间的距离是多少?
-20
1
20
1m
40m
通过本节课的学习,
你学习了哪些知识…
掌握了哪些数学思想方法…
②公式法
将二次函数y=ax2+bx+c转化为y=a(x-h)2+k的形式
①配方法
对称轴:直线x=h
顶点坐标 : (h,k)
对称轴:
顶点坐标 :
③代入法
直线
通过本节课的学习,
你掌握了哪些知识…
应用了哪些数学思想方法…
1.确定下列二次函数的开口方向、对称轴和顶点坐标.
(1)y=2x2-12x+3 (配方法) (2) y=3x2-6x+2(公式法)
(3)y=-5x2+80x-319(代入法)
2.当火箭被竖直向上发射时,它的高度 h (m) 与时间 t(s) 的
关系可以用公式 h=-5t2+150t+10表示,经过多长时间,火箭
到达它的最高点?最高点的高度是多少?
3※若二次函数y=x2+bx+5 配方后为 y=(x-2)2+k,
则k,b的值分别为( )
A. 5,0 B. 1,0 C. 5,-4 D. 1,-4
开口向上
直线x=3
(3,-15)
开口向上
直线x=1
(1,-1)
15s
1135m
D
开口向下
直线x=8
(8, 1)
课本P41 随堂练习 习题2.5 问题解决第4题
※课本P41 数学理解 第2题 问题解决第5题
谢 谢 大家
y=ax2+bx+c (a ≠ 0)
二次函数的顶点式是:
y=a(x-h)2+k (a ≠ 0)
二次函数y=a(x-h)2+k的性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
(h,k)
(h,k)
直线x=h
向上
向下
当x=h时,y有最小值为k.
当x=h时, y有最大值为k.
当x
根据图象填表:
直线x=h
当x
y=a(x-h)2+k(a<0)
y=a(x-h)2+k(a>0)
0
1
2
3
4
5
x
-1
-2
-3
-4
1
2
4
6
8
10
y
2.二次函数 y=2(x+3)2 -5
图象开口 ,对称轴是 ,顶点坐标是 ,当x= 时,y有最 值是 。
向上
直线x=-3
(-3,-5)
-3
小
-5
3.某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个柱子OA,
O恰在水面中心,安置在柱子顶端A处的两个旋转喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任意平面上,抛物线形状如图所示。建立平面直角坐标系,右边一条抛物线水流喷出的高度
y(m)与水面距离x(m)之间的关系式是
(1)喷出的水流距水平面的最大高度是 米;
(2)两条水流最高点之间的距离是 米。
1
2
-1
生活中的数学
y=2x2-8x+7
y=a(x-h)2+k
转化
?
用配方法求二次函数y=2x2-8x+7图象的
对称轴和顶点坐标。
2.用配方法将二次函数由一般式转化为顶点式的步骤:
①提二次项系数;
1.选择最优的解题方法
题后反思:
②配方;
③化简
用配方法确定下列二次函数图象的对称轴
和顶点坐标。
(1) y=3x2-6x+7 (2) y=-2x2-12x+8
求二次函数y=ax?+bx+c图象的对称轴和顶点坐标.
顶点式
y=a(x-h)2 +k
二次函数y=ax2+bx+c (a ≠ 0)的图象是一条抛物线
用公式法求二次函数y=2x2-8x+7图象的
对称轴和顶点坐标。
根据公式法确定下列二次函数图象的对称轴和顶点坐标。
y=2x2-4x-1
如图,桥梁的两条钢缆具有相同的抛物线形状,而且左、右两条抛物线关于y轴对称。按照图中的直角坐标系,左面的一条抛物线可以用
表示.
(1)钢缆的最低点到桥面的距离是多少?
(2)两条钢缆最低点之间的距离是多少?
-20
1
20
1m
40m
通过本节课的学习,
你学习了哪些知识…
掌握了哪些数学思想方法…
②公式法
将二次函数y=ax2+bx+c转化为y=a(x-h)2+k的形式
①配方法
对称轴:直线x=h
顶点坐标 : (h,k)
对称轴:
顶点坐标 :
③代入法
直线
通过本节课的学习,
你掌握了哪些知识…
应用了哪些数学思想方法…
1.确定下列二次函数的开口方向、对称轴和顶点坐标.
(1)y=2x2-12x+3 (配方法) (2) y=3x2-6x+2(公式法)
(3)y=-5x2+80x-319(代入法)
2.当火箭被竖直向上发射时,它的高度 h (m) 与时间 t(s) 的
关系可以用公式 h=-5t2+150t+10表示,经过多长时间,火箭
到达它的最高点?最高点的高度是多少?
3※若二次函数y=x2+bx+5 配方后为 y=(x-2)2+k,
则k,b的值分别为( )
A. 5,0 B. 1,0 C. 5,-4 D. 1,-4
开口向上
直线x=3
(3,-15)
开口向上
直线x=1
(1,-1)
15s
1135m
D
开口向下
直线x=8
(8, 1)
课本P41 随堂练习 习题2.5 问题解决第4题
※课本P41 数学理解 第2题 问题解决第5题
谢 谢 大家
