第1部分 第3讲平面向量和复数-2021届高三高考数学二轮复习课件(80张PPT)
文档属性
| 名称 | 第1部分 第3讲平面向量和复数-2021届高三高考数学二轮复习课件(80张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 21:30:57 | ||
图片预览








文档简介
第一部分
方法篇?素养形成(文理)
第3讲 平面向量和复数(文理)
1 解题策略 · 明方向
2 考点分类 · 析重点
3 易错清零 · 免失误
4 真题回放 · 悟高考
5 预测演练 · 巧押题
1.高考中主要考查平面向量基本定理、向量的运算及平面向量共线的坐标表示.
2.主要考查复数的基本概念、复数的四则运算,及复数的几何意义.
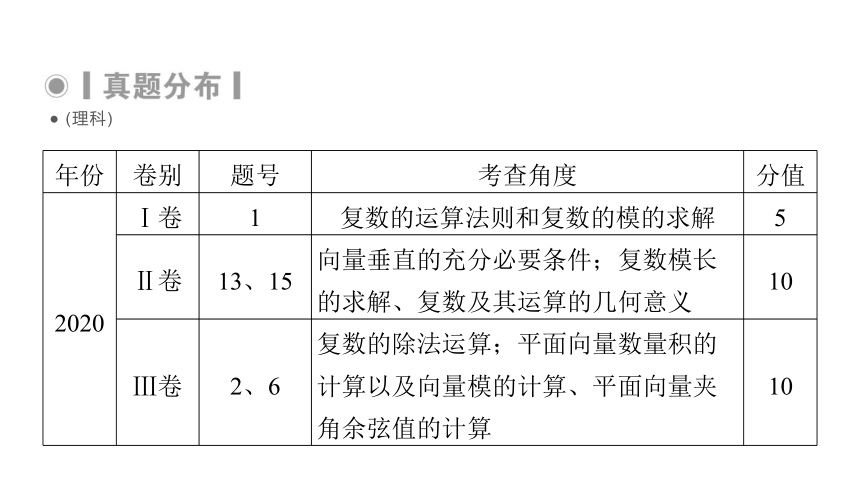
(理科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
1
复数的运算法则和复数的模的求解
5
Ⅱ卷
13、15
向量垂直的充分必要条件;复数模长的求解、复数及其运算的几何意义
10
Ⅲ卷
2、6
复数的除法运算;平面向量数量积的计算以及向量模的计算、平面向量夹角余弦值的计算
10
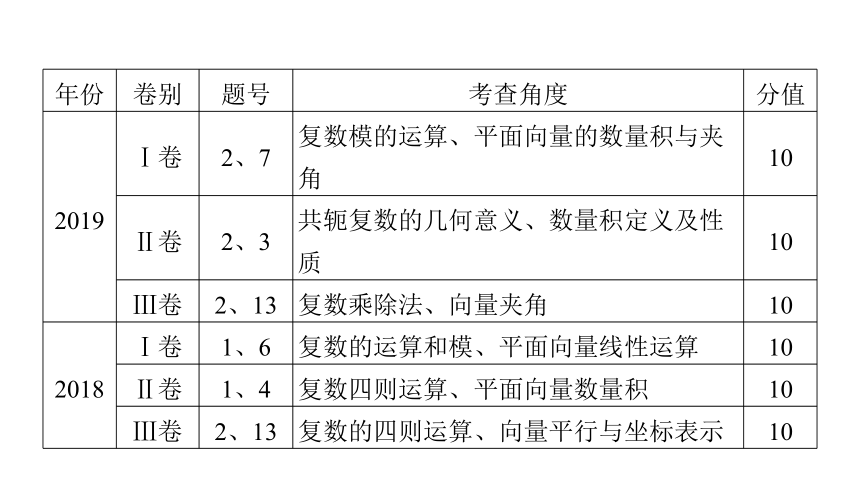
年份
卷别
题号
考查角度
分值
2019
Ⅰ卷
2、7
复数模的运算、平面向量的数量积与夹角
10
Ⅱ卷
2、3
共轭复数的几何意义、数量积定义及性质
10
Ⅲ卷
2、13
复数乘除法、向量夹角
10
2018
Ⅰ卷
1、6
复数的运算和模、平面向量线性运算
10
Ⅱ卷
1、4
复数四则运算、平面向量数量积
10
Ⅲ卷
2、13
复数的四则运算、向量平行与坐标表示
10
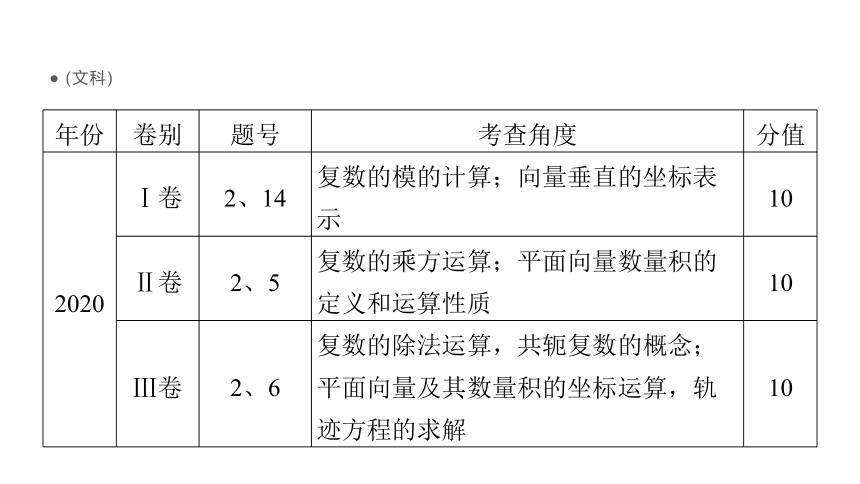
(文科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
2、14
复数的模的计算;向量垂直的坐标表示
10
Ⅱ卷
2、5
复数的乘方运算;平面向量数量积的定义和运算性质
10
Ⅲ卷
2、6
复数的除法运算,共轭复数的概念;平面向量及其数量积的坐标运算,轨迹方程的求解
10
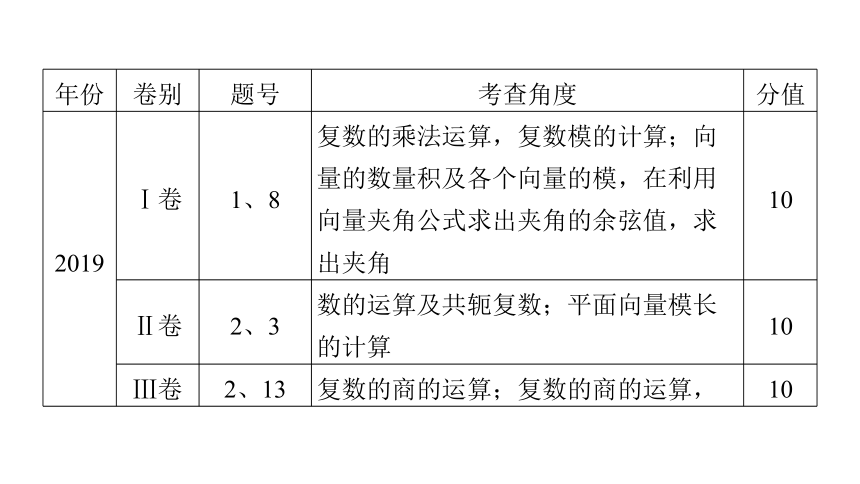
年份
卷别
题号
考查角度
分值
2019
Ⅰ卷
1、8
复数的乘法运算,复数模的计算;向量的数量积及各个向量的模,在利用向量夹角公式求出夹角的余弦值,求出夹角
10
Ⅱ卷
2、3
数的运算及共轭复数;平面向量模长的计算
10
Ⅲ卷
2、13
复数的商的运算;复数的商的运算,
10
年份
卷别
题号
考查角度
分值
2018
Ⅰ卷
1、7
复数模的计算;平面向量基本定理
10
Ⅱ卷
1、4
复数的乘法运算;向量模的性质以及向量乘法
10
Ⅲ卷
2、13
复数的四则运算;向量的坐标运算,以及两向量共线
10
02 考点分类 · 析重点
1.平面向量的线性运算
(1)常用的法则是平行四边形法则和三角形法则,一般共起点的向量求和用平行四边形法则,求差用三角形法则,求首尾相连的向量的和用三角形法则.
(2)找出图形中的相等向量、共线向量,将所求向量与已知向量转化到同一个平行四边形或三角形中求解.
考点一 平面向量的线性运算
3.平面向量的基本定理
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.其中,不共线的向量e1,e2叫做表示这一平面内所有向量的一组基底.
考向1 平面向量的线性运算
C
A
B
4.(2020·淮南二模)已知向量a=(m,1),b=(3,3).
若(a-b)⊥b,则实数m=____.
【解析】 因为(a-b)⊥b,故(a-b)·b=0,
即3m+3-18=0,故m=5.
5
平面向量线性运算的两个技巧
(1)对于平面向量的线性运算问题,要尽可能转化到三角形或平行四边形中,灵活运用三角形法则、平行四边形法则,紧密结合图形的几何性质进行运算.
(2)在证明两向量平行时,若已知两向量的坐标形式,常利用坐标运算来判断;若两向量不是以坐标形式呈现的,常利用共线向量定理(当b≠0时,a∥b?存在唯一实数λ,使得a=λb)来判断.
1.平面向量数量积的性质及其坐标表示
已知非零向量a=(x1,y1),b=(x2,y2),a与b的夹角为θ.
考点二 平面向量的数量积
2.平面向量数量积的运算律
(1)a·b=b·a(交换律).
(2)λa·b=λ(a·b)=a·(λb)(结合律).
(3)(a+b)·c=a·c+b·c(分配律).
B
14
B
C
D
D
1.解决以平面图形为载体的向量数量积问题的方法
(1)选择平面图形中模与夹角确定的向量作为一组基底,用该基底表示构成数量积的两个向量,结合向量数量积运算律求解.
(2)若已知图形中有明显的适合建立直角坐标系的条件,可建立直角坐标系将向量数量积运算转化为代数运算来解决.
2.求两向量夹角应注意
两个向量夹角的范围是[0,π],在使用平面向量解决问题时要特别注意两个向量夹角可能是0或π的情况,如已知两个向量的夹角为钝角时,不仅要求其数量积小于零,还要求不能反向共线.
1.复数的运算法则
设z1=a+bi,z2=c+di(a,b,c,d∈R),则:
(1)z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i;
(2)z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i;
考点三 复数
A
D
D
4.(2020·江苏省扬州市调研)若(3+i)z=2-i(i为虚数单位),则复
数z=__________.
C
6.(2020·北京昌平区期末)在复平面内,复数i(i-1)对应的点位于
( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】 ∵i(i-1)=i2-i=-1-i,在复平面内对应的点的坐标为(-1,-1),位于第三象限,故选C.
C
掌握复数代数形式运算的方法
(1)复数的乘法:复数的乘法类似于多项式的四则运算,可将含有虚数单位i的看作一类项,不含i的看作另一类项,分别合并同类项即可.
(2)复数的除法:除法的关键是分子分母同乘以分母的共轭复数,解题时要注意把i的幂写成最简形式.复数的除法类似初中所学化简分数常用的“分母有理化”,其实质就是“分母实数化”.
03 易错清零 · 免失误
典例1
1.混淆向量共线与向量垂直的坐标表示
C
【剖析】 以上错误把向量共线的坐标表示利用成向量垂直的坐标表示,导致结果错误.
【错解】 a与b的夹角为锐角,∴a·b>0,∴-2λ+2>0,解得λ<1,
故选D.
典例2
2.忽视两向量的夹角的范围
B
【剖析】 上述解法的错误就是忽略了向量夹角的范围是[0,π],而夹角为0时数量积也是大于0的,应该排除.
典例3
3.错用复数运算法则
D
典例4
4.不能正确理解复数的几何意义
A
04 真题回放 · 悟高考
【解析】 由题意可得:
z2=(1+i)2=2i,则z2-2z=2i-2(1+i)=-2.
故|z2-2z|=|-2|=2.
故选D.
D
C
2.(文)(2020·全国卷Ⅱ卷)(1-i)4= ( )
A.-4 B.4
C.-4i D.4i
【解析】 (1-i)4=[(1-i)2]2=(1-2i+i2)2=(-2i)2=-4.
A
C
D
4.(理)(2020·全国卷Ⅲ卷)若z(1+i)=2i,则z= ( )
A.-1-i B.-1+i
C.1-i D.1+i
D
4.(文)(2020·全国卷Ⅱ卷)已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是 ( )
A.a+2b B.2a+b
C.a-2b D.2a-b
D
5.(理)(2019·全国卷Ⅰ)设复数|z-i|=1,z在复平面内对应的点为(x,y),则 ( )
A.(x+1)2+y2=1 B.(x-1)2+y2=1
C.x2+(y-1)2=1 D.x2+(y+1)2=1
C
A
C
A
D
B
C
9.(理)(2020·全国卷Ⅰ卷)设a,b为单位向量,且|a+b|=1,则|a-b|=_____.
9.(文)(2020·全国卷Ⅰ卷)设向量a=(1,-1),b=(m+1,2m-4),若a⊥b,则m=____.
【解析】 由a⊥b可得a·b=0,
又因为a=(1,-1),b=(m+1,2m-4),
所以a·b=1·(m+1)+(-1)·(2m-4)=0,
即m=5.
5
10.(文)(2019·全国卷Ⅲ)已知向量a=(2,2),b=(-8,6),则cos〈a,
b〉=_______.
方法篇?素养形成(文理)
第3讲 平面向量和复数(文理)
1 解题策略 · 明方向
2 考点分类 · 析重点
3 易错清零 · 免失误
4 真题回放 · 悟高考
5 预测演练 · 巧押题
1.高考中主要考查平面向量基本定理、向量的运算及平面向量共线的坐标表示.
2.主要考查复数的基本概念、复数的四则运算,及复数的几何意义.
(理科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
1
复数的运算法则和复数的模的求解
5
Ⅱ卷
13、15
向量垂直的充分必要条件;复数模长的求解、复数及其运算的几何意义
10
Ⅲ卷
2、6
复数的除法运算;平面向量数量积的计算以及向量模的计算、平面向量夹角余弦值的计算
10
年份
卷别
题号
考查角度
分值
2019
Ⅰ卷
2、7
复数模的运算、平面向量的数量积与夹角
10
Ⅱ卷
2、3
共轭复数的几何意义、数量积定义及性质
10
Ⅲ卷
2、13
复数乘除法、向量夹角
10
2018
Ⅰ卷
1、6
复数的运算和模、平面向量线性运算
10
Ⅱ卷
1、4
复数四则运算、平面向量数量积
10
Ⅲ卷
2、13
复数的四则运算、向量平行与坐标表示
10
(文科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
2、14
复数的模的计算;向量垂直的坐标表示
10
Ⅱ卷
2、5
复数的乘方运算;平面向量数量积的定义和运算性质
10
Ⅲ卷
2、6
复数的除法运算,共轭复数的概念;平面向量及其数量积的坐标运算,轨迹方程的求解
10
年份
卷别
题号
考查角度
分值
2019
Ⅰ卷
1、8
复数的乘法运算,复数模的计算;向量的数量积及各个向量的模,在利用向量夹角公式求出夹角的余弦值,求出夹角
10
Ⅱ卷
2、3
数的运算及共轭复数;平面向量模长的计算
10
Ⅲ卷
2、13
复数的商的运算;复数的商的运算,
10
年份
卷别
题号
考查角度
分值
2018
Ⅰ卷
1、7
复数模的计算;平面向量基本定理
10
Ⅱ卷
1、4
复数的乘法运算;向量模的性质以及向量乘法
10
Ⅲ卷
2、13
复数的四则运算;向量的坐标运算,以及两向量共线
10
02 考点分类 · 析重点
1.平面向量的线性运算
(1)常用的法则是平行四边形法则和三角形法则,一般共起点的向量求和用平行四边形法则,求差用三角形法则,求首尾相连的向量的和用三角形法则.
(2)找出图形中的相等向量、共线向量,将所求向量与已知向量转化到同一个平行四边形或三角形中求解.
考点一 平面向量的线性运算
3.平面向量的基本定理
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.其中,不共线的向量e1,e2叫做表示这一平面内所有向量的一组基底.
考向1 平面向量的线性运算
C
A
B
4.(2020·淮南二模)已知向量a=(m,1),b=(3,3).
若(a-b)⊥b,则实数m=____.
【解析】 因为(a-b)⊥b,故(a-b)·b=0,
即3m+3-18=0,故m=5.
5
平面向量线性运算的两个技巧
(1)对于平面向量的线性运算问题,要尽可能转化到三角形或平行四边形中,灵活运用三角形法则、平行四边形法则,紧密结合图形的几何性质进行运算.
(2)在证明两向量平行时,若已知两向量的坐标形式,常利用坐标运算来判断;若两向量不是以坐标形式呈现的,常利用共线向量定理(当b≠0时,a∥b?存在唯一实数λ,使得a=λb)来判断.
1.平面向量数量积的性质及其坐标表示
已知非零向量a=(x1,y1),b=(x2,y2),a与b的夹角为θ.
考点二 平面向量的数量积
2.平面向量数量积的运算律
(1)a·b=b·a(交换律).
(2)λa·b=λ(a·b)=a·(λb)(结合律).
(3)(a+b)·c=a·c+b·c(分配律).
B
14
B
C
D
D
1.解决以平面图形为载体的向量数量积问题的方法
(1)选择平面图形中模与夹角确定的向量作为一组基底,用该基底表示构成数量积的两个向量,结合向量数量积运算律求解.
(2)若已知图形中有明显的适合建立直角坐标系的条件,可建立直角坐标系将向量数量积运算转化为代数运算来解决.
2.求两向量夹角应注意
两个向量夹角的范围是[0,π],在使用平面向量解决问题时要特别注意两个向量夹角可能是0或π的情况,如已知两个向量的夹角为钝角时,不仅要求其数量积小于零,还要求不能反向共线.
1.复数的运算法则
设z1=a+bi,z2=c+di(a,b,c,d∈R),则:
(1)z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i;
(2)z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i;
考点三 复数
A
D
D
4.(2020·江苏省扬州市调研)若(3+i)z=2-i(i为虚数单位),则复
数z=__________.
C
6.(2020·北京昌平区期末)在复平面内,复数i(i-1)对应的点位于
( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】 ∵i(i-1)=i2-i=-1-i,在复平面内对应的点的坐标为(-1,-1),位于第三象限,故选C.
C
掌握复数代数形式运算的方法
(1)复数的乘法:复数的乘法类似于多项式的四则运算,可将含有虚数单位i的看作一类项,不含i的看作另一类项,分别合并同类项即可.
(2)复数的除法:除法的关键是分子分母同乘以分母的共轭复数,解题时要注意把i的幂写成最简形式.复数的除法类似初中所学化简分数常用的“分母有理化”,其实质就是“分母实数化”.
03 易错清零 · 免失误
典例1
1.混淆向量共线与向量垂直的坐标表示
C
【剖析】 以上错误把向量共线的坐标表示利用成向量垂直的坐标表示,导致结果错误.
【错解】 a与b的夹角为锐角,∴a·b>0,∴-2λ+2>0,解得λ<1,
故选D.
典例2
2.忽视两向量的夹角的范围
B
【剖析】 上述解法的错误就是忽略了向量夹角的范围是[0,π],而夹角为0时数量积也是大于0的,应该排除.
典例3
3.错用复数运算法则
D
典例4
4.不能正确理解复数的几何意义
A
04 真题回放 · 悟高考
【解析】 由题意可得:
z2=(1+i)2=2i,则z2-2z=2i-2(1+i)=-2.
故|z2-2z|=|-2|=2.
故选D.
D
C
2.(文)(2020·全国卷Ⅱ卷)(1-i)4= ( )
A.-4 B.4
C.-4i D.4i
【解析】 (1-i)4=[(1-i)2]2=(1-2i+i2)2=(-2i)2=-4.
A
C
D
4.(理)(2020·全国卷Ⅲ卷)若z(1+i)=2i,则z= ( )
A.-1-i B.-1+i
C.1-i D.1+i
D
4.(文)(2020·全国卷Ⅱ卷)已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是 ( )
A.a+2b B.2a+b
C.a-2b D.2a-b
D
5.(理)(2019·全国卷Ⅰ)设复数|z-i|=1,z在复平面内对应的点为(x,y),则 ( )
A.(x+1)2+y2=1 B.(x-1)2+y2=1
C.x2+(y-1)2=1 D.x2+(y+1)2=1
C
A
C
A
D
B
C
9.(理)(2020·全国卷Ⅰ卷)设a,b为单位向量,且|a+b|=1,则|a-b|=_____.
9.(文)(2020·全国卷Ⅰ卷)设向量a=(1,-1),b=(m+1,2m-4),若a⊥b,则m=____.
【解析】 由a⊥b可得a·b=0,
又因为a=(1,-1),b=(m+1,2m-4),
所以a·b=1·(m+1)+(-1)·(2m-4)=0,
即m=5.
5
10.(文)(2019·全国卷Ⅲ)已知向量a=(2,2),b=(-8,6),则cos〈a,
b〉=_______.
同课章节目录
