第1部分 第5讲排列、组合、二项式定理-2021届高三高考数学二轮复习课件(66张PPT)
文档属性
| 名称 | 第1部分 第5讲排列、组合、二项式定理-2021届高三高考数学二轮复习课件(66张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 21:29:45 | ||
图片预览











文档简介
第一部分
方法篇?素养形成(文理)
第5讲 排列、组合、二项式定理(理)
1 解题策略 · 明方向
2 考点分类 · 析重点
3 易错清零 · 免失误
4 真题回放 · 悟高考
5 预测演练 · 巧押题
1.以理解和应用排列、组合的概念为主,常常以实际问题为载体,考查解决问题的能力.
2.以理解和应用二项式定理为主,常考查二项展开式,通项公式以及二项式系数的性质,赋值法求系数的和也是考查的热点.
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
8
二项式定理及其展开式的通项公式
5
Ⅱ卷
14
排列组合解决实际问题
5
Ⅲ卷
14
二项式定理,利用通项公式求二项展开式中的指定项
5
年份
卷别
题号
考查角度
分值
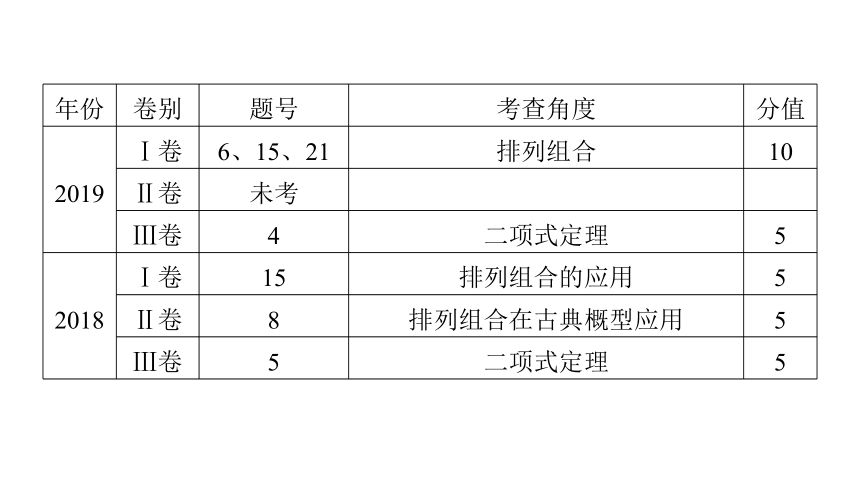
2019
Ⅰ卷
6、15、21
排列组合
10
Ⅱ卷
未考
?
?
Ⅲ卷
4
二项式定理
5
2018
Ⅰ卷
15
排列组合的应用
5
Ⅱ卷
8
排列组合在古典概型应用
5
Ⅲ卷
5
二项式定理
5
02 考点分类 · 析重点
排列数、组合数的定义、公式、性质
考点一 排列、组合的应用
?
排列数
组合数
定
义
从n个不同元素中取出m(m≤n,m,n∈N*)个元素的所有不同排列的个数
从n个不同元素中取出m(m≤n,m,n∈N*)个元素的所有不同组合的个数
考向1 带附加条件的排列、组合问题
1.(2020·辽宁省沈阳市实验中学月考)将6枚硬币放入如图所示的9个方格中,要求每个方格中至多放一枚硬币,并且每行每列都有2枚硬币,则放置硬币的方法共有几种 ( )
A.6
B.12
C.18
D.36
A
【解析】 先在第一列里任意选一格不放硬币,有3种选法;再在第二列选一格(不能选与第一步同行的空格)不放硬币,有2种选法;最后在第三列选一格(不能选与第一、二步同行的空格)不放硬币,有1种方法.所以共有3×2×1=6种方法.故选A.
2.(2020·北京东城区期末)从数字1,2,3,4,5中,取出3个数字(允许重复),组成三位数,各位数字之和等于6,这样的三位数的个数为
( )
A.7 B.9 C.10 D.13
C
3.(2020·山西四校联考)高三要安排毕业晚会的4个音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求2个舞蹈节目不连排,则不同排法的种数是 ( )
A.1 800 B.3 600 C.4 320 D.5 040
B
考向2 分组、分配问题
4.(2020·北京市朝阳区高三上期末)从3名教师和5名学生中,选出4人参加“我和我的祖国”快闪活动.要求至少有一名教师入选,且入选教师人数不多于入选学生人数,则不同的选派方案的种数是
( )
A.20 B.40 C.60 D.120
C
5.(2020·合肥模拟)现有三本相同的语文书和一本数学书,分发给三个学生,每个学生至少分得一本,不同分法的种数为 ( )
A.36 B.9 C.18 D.15
B
6.(2020·恩施质检)将4位女生和4位男生分为两组参加不同的两个兴趣小组,一组3个男生1个女生,余下的组成另外一组,则不同的选法共有_____种(用数字填写答案).
32
求解有限制条件排列问题的主要方法
(1)直接法:①分类法:选定一个适当的分类标准,将要完成的事件分成几个类型,分别计算每个类型中的排列数,再由分类加法计数原理得出总数.②分步法:选定一个适当的标准,将事件分成几个步骤来完成,分别计算出各步骤的排列数,再由分步乘法计数原理得出总数.
(2)捆绑法:相邻问题捆绑处理,即可以把相邻元素看作一个整体与其他元素进行排列,同时注意捆绑元素的内部排列.
(3)插空法:不相邻问题插空处理,即先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列后的空中.
(4)除法:对于定序问题,可先不考虑顺序限制,排列后,再除以已定元素的全排列.
(5)间接法:对于分类过多的问题,一般利用正难则反、等价转化的方法.
考点二 二项式定理
B
C
B
C
B
15
考向3 赋值问题
7.(2020·益阳调研)若(1-3x)2 020=a0+a1x+…+a2 020x2 020,x∈R,则a1·3+a2·32+…+a2 020·32 020的值为 ( )
A.22 020-1 B.82 020-1
C.22 020 D.82 020
【解析】 由已知,令x=0,得a0=1,令x=3,得a0+a1·3+a2·32+…+a2 020·32 020=(1-9)2 020=82 020,所以a1·3+a2·32+…+a2 020·32 020=82 020-a0=82 020-1,故选B.
B
8.(2020·衢州五校联考)若(3x-1)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a1=_____,a0+a1+a2+a3+a4+a5=_____.
15
32
1.求二项式与代数式积的展开式特定项系数问题的关键
一是将二项式看作一个整体,利用分配律整理所给式子;二是利用二项展开式的通项公式,求特定项,特定项的系数即为所要求的系数.
2.求(x+y+z)n的展开式的特定项的系数问题的技巧
若三项能用完全平方公式,那当然比较简单,若三项不能用完全平方公式,只需根据题目特点,把“三项”当成“两项”看,再利用二项展开式的通项公式去求特定项的系数;把(x+y+z)n看作n个因式x+y+z的乘积,再利用组合数公式求解.
03 易错清零 · 免失误
为适应高考改革,某学校在一次模拟测试中实行“3+1+2”模式,其中“3”指语文、数学、外语三门必考科目,“1”指在物理、历史两门科目中必选一门,“2”指在化学、生物、政治、地理以及除了“1”中已选的一门以外的历史或物理这五门科目中任意选择两门,则一名学生的不同选科组合有 ( )
A.8种 B.12种 C.16种 D.20种
典例1
1.混淆“分类”与“分步”
C
【剖析】 上述解法的错误主要是审题不清,不能正确的分类,误以为“1”是只能从物理和历史中选1门,从而漏掉物理和历史全选,而导致错误;二是此题不仅是分步,更重要的分类,只利用了分步而没有分类,导致错误.
典例2
2.混淆“排列”与“组合”
D
(3)2+2+2显然2根算筹可以表示2个不同的数字,故不同的三位数有2×2×2=8(个).
综上,可以用六根算筹表示的不含0的三位数共有6+24+8=38(个).
故选D.
【剖析】 该题的易错点主要有两个:一是不能正确理解“三位数”对顺序的要求,误以为只是组合问题,只需将六根算筹分成三份即可,导致错解;二是忽视“算筹根数不是1时,可以表示2个不同的数字”,导致漏解.区别组合问题与排列问题的关键是“顺序”,排列是有顺序的,组合是没有顺序的.
(2020·福州八中10月月考)在乌镇举行的第六届世界互联网大会中,为了提高安保的级别同时又方便接待,对其中的五个参会国的人员安排酒店住宿,这五个参会国要在a,b,c三家酒店中选择一家,且每家酒店至少有一个参会国入住,则不同的安排方法共有 ( )
A.124种 B.130种 C.150种 D.240种
典例3
3.忽略“平均分组”与“非平均分组”的差异
C
【剖析】 上述解法的错误主要是不能正确处理分组问题,显然将5个参会国分为1,1,3和2,2,1三组,都涉及部分均分,但整体不是均分,故易误认为只需利用组合数公式直接逐组选出即可求解,忽视部分组中元素个数相等而出现的部分均分问题,只要出现两组(或组数大于2)的元素个数相等,就是均分问题.如果各组元素个数都相等,就是整体均分;如果部分组元素个数相等,就是部分均分.
典例4
4.错用二项展开式的通项公式
B
(2020·山东济南外国语学校10月月考)已知x(x-2)8=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)9,则a1+a2+…+a9=______,a2=_____.
典例5
5.混淆二项式系数与展开式的项的系数
-1
20
【剖析】 该题的易错点有两个:一是混淆展开式的项的系数与二项式系数,误以为a1,a2,…,a9是二项式系数,导致错误;二是不能正确理解展开式的形式,前后形式不一致,导致解题没有思路.求解二项展开式中某些项的系数之和,可以直接利用赋值法求解,求值时注意展开式与所求式子之间的对应,从而进行恰当赋值,不是求任意项的系数之和都是令x=1,抓住对应关系是关键,如该题中要得到a0+a1+a2+…+a9,必须令x=2;而求a0,就需要令x=1.
04 真题回放 · 悟高考
C
2.(2017·全国卷Ⅱ)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有 ( )
A.12种 B.18种 C.24种 D.36种
D
3.(2016·全国卷Ⅱ)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为 ( )
A.24
B.18
C.12
D.9
【解析】 由题意可知E→F共有6种走法,F→G共有3种走法,由乘法计数原理知,共有6×3=18种走法,故选B.
B
4.(2018·全国卷Ⅰ)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有_____种.(用数字填写答案)
16
5.(2019·全国卷Ⅲ)(1+2x2)(1+x)4的展开式中x3的系数为 ( )
A.12 B.16 C.20 D.24
A
C
C
8.(2017·全国卷Ⅲ)(x+y)(2x-y)5的展开式中x3y3的系数为 ( )
A.-80 B.-40 C.40 D.80
C
9.(2020·全国卷Ⅱ卷)4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,则不同的安排方法共有_____种.
36
240
方法篇?素养形成(文理)
第5讲 排列、组合、二项式定理(理)
1 解题策略 · 明方向
2 考点分类 · 析重点
3 易错清零 · 免失误
4 真题回放 · 悟高考
5 预测演练 · 巧押题
1.以理解和应用排列、组合的概念为主,常常以实际问题为载体,考查解决问题的能力.
2.以理解和应用二项式定理为主,常考查二项展开式,通项公式以及二项式系数的性质,赋值法求系数的和也是考查的热点.
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
8
二项式定理及其展开式的通项公式
5
Ⅱ卷
14
排列组合解决实际问题
5
Ⅲ卷
14
二项式定理,利用通项公式求二项展开式中的指定项
5
年份
卷别
题号
考查角度
分值
2019
Ⅰ卷
6、15、21
排列组合
10
Ⅱ卷
未考
?
?
Ⅲ卷
4
二项式定理
5
2018
Ⅰ卷
15
排列组合的应用
5
Ⅱ卷
8
排列组合在古典概型应用
5
Ⅲ卷
5
二项式定理
5
02 考点分类 · 析重点
排列数、组合数的定义、公式、性质
考点一 排列、组合的应用
?
排列数
组合数
定
义
从n个不同元素中取出m(m≤n,m,n∈N*)个元素的所有不同排列的个数
从n个不同元素中取出m(m≤n,m,n∈N*)个元素的所有不同组合的个数
考向1 带附加条件的排列、组合问题
1.(2020·辽宁省沈阳市实验中学月考)将6枚硬币放入如图所示的9个方格中,要求每个方格中至多放一枚硬币,并且每行每列都有2枚硬币,则放置硬币的方法共有几种 ( )
A.6
B.12
C.18
D.36
A
【解析】 先在第一列里任意选一格不放硬币,有3种选法;再在第二列选一格(不能选与第一步同行的空格)不放硬币,有2种选法;最后在第三列选一格(不能选与第一、二步同行的空格)不放硬币,有1种方法.所以共有3×2×1=6种方法.故选A.
2.(2020·北京东城区期末)从数字1,2,3,4,5中,取出3个数字(允许重复),组成三位数,各位数字之和等于6,这样的三位数的个数为
( )
A.7 B.9 C.10 D.13
C
3.(2020·山西四校联考)高三要安排毕业晚会的4个音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求2个舞蹈节目不连排,则不同排法的种数是 ( )
A.1 800 B.3 600 C.4 320 D.5 040
B
考向2 分组、分配问题
4.(2020·北京市朝阳区高三上期末)从3名教师和5名学生中,选出4人参加“我和我的祖国”快闪活动.要求至少有一名教师入选,且入选教师人数不多于入选学生人数,则不同的选派方案的种数是
( )
A.20 B.40 C.60 D.120
C
5.(2020·合肥模拟)现有三本相同的语文书和一本数学书,分发给三个学生,每个学生至少分得一本,不同分法的种数为 ( )
A.36 B.9 C.18 D.15
B
6.(2020·恩施质检)将4位女生和4位男生分为两组参加不同的两个兴趣小组,一组3个男生1个女生,余下的组成另外一组,则不同的选法共有_____种(用数字填写答案).
32
求解有限制条件排列问题的主要方法
(1)直接法:①分类法:选定一个适当的分类标准,将要完成的事件分成几个类型,分别计算每个类型中的排列数,再由分类加法计数原理得出总数.②分步法:选定一个适当的标准,将事件分成几个步骤来完成,分别计算出各步骤的排列数,再由分步乘法计数原理得出总数.
(2)捆绑法:相邻问题捆绑处理,即可以把相邻元素看作一个整体与其他元素进行排列,同时注意捆绑元素的内部排列.
(3)插空法:不相邻问题插空处理,即先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列后的空中.
(4)除法:对于定序问题,可先不考虑顺序限制,排列后,再除以已定元素的全排列.
(5)间接法:对于分类过多的问题,一般利用正难则反、等价转化的方法.
考点二 二项式定理
B
C
B
C
B
15
考向3 赋值问题
7.(2020·益阳调研)若(1-3x)2 020=a0+a1x+…+a2 020x2 020,x∈R,则a1·3+a2·32+…+a2 020·32 020的值为 ( )
A.22 020-1 B.82 020-1
C.22 020 D.82 020
【解析】 由已知,令x=0,得a0=1,令x=3,得a0+a1·3+a2·32+…+a2 020·32 020=(1-9)2 020=82 020,所以a1·3+a2·32+…+a2 020·32 020=82 020-a0=82 020-1,故选B.
B
8.(2020·衢州五校联考)若(3x-1)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a1=_____,a0+a1+a2+a3+a4+a5=_____.
15
32
1.求二项式与代数式积的展开式特定项系数问题的关键
一是将二项式看作一个整体,利用分配律整理所给式子;二是利用二项展开式的通项公式,求特定项,特定项的系数即为所要求的系数.
2.求(x+y+z)n的展开式的特定项的系数问题的技巧
若三项能用完全平方公式,那当然比较简单,若三项不能用完全平方公式,只需根据题目特点,把“三项”当成“两项”看,再利用二项展开式的通项公式去求特定项的系数;把(x+y+z)n看作n个因式x+y+z的乘积,再利用组合数公式求解.
03 易错清零 · 免失误
为适应高考改革,某学校在一次模拟测试中实行“3+1+2”模式,其中“3”指语文、数学、外语三门必考科目,“1”指在物理、历史两门科目中必选一门,“2”指在化学、生物、政治、地理以及除了“1”中已选的一门以外的历史或物理这五门科目中任意选择两门,则一名学生的不同选科组合有 ( )
A.8种 B.12种 C.16种 D.20种
典例1
1.混淆“分类”与“分步”
C
【剖析】 上述解法的错误主要是审题不清,不能正确的分类,误以为“1”是只能从物理和历史中选1门,从而漏掉物理和历史全选,而导致错误;二是此题不仅是分步,更重要的分类,只利用了分步而没有分类,导致错误.
典例2
2.混淆“排列”与“组合”
D
(3)2+2+2显然2根算筹可以表示2个不同的数字,故不同的三位数有2×2×2=8(个).
综上,可以用六根算筹表示的不含0的三位数共有6+24+8=38(个).
故选D.
【剖析】 该题的易错点主要有两个:一是不能正确理解“三位数”对顺序的要求,误以为只是组合问题,只需将六根算筹分成三份即可,导致错解;二是忽视“算筹根数不是1时,可以表示2个不同的数字”,导致漏解.区别组合问题与排列问题的关键是“顺序”,排列是有顺序的,组合是没有顺序的.
(2020·福州八中10月月考)在乌镇举行的第六届世界互联网大会中,为了提高安保的级别同时又方便接待,对其中的五个参会国的人员安排酒店住宿,这五个参会国要在a,b,c三家酒店中选择一家,且每家酒店至少有一个参会国入住,则不同的安排方法共有 ( )
A.124种 B.130种 C.150种 D.240种
典例3
3.忽略“平均分组”与“非平均分组”的差异
C
【剖析】 上述解法的错误主要是不能正确处理分组问题,显然将5个参会国分为1,1,3和2,2,1三组,都涉及部分均分,但整体不是均分,故易误认为只需利用组合数公式直接逐组选出即可求解,忽视部分组中元素个数相等而出现的部分均分问题,只要出现两组(或组数大于2)的元素个数相等,就是均分问题.如果各组元素个数都相等,就是整体均分;如果部分组元素个数相等,就是部分均分.
典例4
4.错用二项展开式的通项公式
B
(2020·山东济南外国语学校10月月考)已知x(x-2)8=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)9,则a1+a2+…+a9=______,a2=_____.
典例5
5.混淆二项式系数与展开式的项的系数
-1
20
【剖析】 该题的易错点有两个:一是混淆展开式的项的系数与二项式系数,误以为a1,a2,…,a9是二项式系数,导致错误;二是不能正确理解展开式的形式,前后形式不一致,导致解题没有思路.求解二项展开式中某些项的系数之和,可以直接利用赋值法求解,求值时注意展开式与所求式子之间的对应,从而进行恰当赋值,不是求任意项的系数之和都是令x=1,抓住对应关系是关键,如该题中要得到a0+a1+a2+…+a9,必须令x=2;而求a0,就需要令x=1.
04 真题回放 · 悟高考
C
2.(2017·全国卷Ⅱ)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有 ( )
A.12种 B.18种 C.24种 D.36种
D
3.(2016·全国卷Ⅱ)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为 ( )
A.24
B.18
C.12
D.9
【解析】 由题意可知E→F共有6种走法,F→G共有3种走法,由乘法计数原理知,共有6×3=18种走法,故选B.
B
4.(2018·全国卷Ⅰ)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有_____种.(用数字填写答案)
16
5.(2019·全国卷Ⅲ)(1+2x2)(1+x)4的展开式中x3的系数为 ( )
A.12 B.16 C.20 D.24
A
C
C
8.(2017·全国卷Ⅲ)(x+y)(2x-y)5的展开式中x3y3的系数为 ( )
A.-80 B.-40 C.40 D.80
C
9.(2020·全国卷Ⅱ卷)4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,则不同的安排方法共有_____种.
36
240
同课章节目录
