第1部分 第2讲集合与常用逻辑用语-2021届高三高考数学二轮复习课件(72张PPT)
文档属性
| 名称 | 第1部分 第2讲集合与常用逻辑用语-2021届高三高考数学二轮复习课件(72张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 21:09:14 | ||
图片预览










文档简介
第一部分
方法篇?素养形成(文理)
第2讲 集合与常用逻辑用语(文理)
1 解题策略 · 明方向
2 考点分类 · 析重点
3 易错清零 · 免失误
4 真题回放 · 悟高考
5 预测演练 · 巧押题
1.本部分作为高考必考内容,仍会以选择题的形式在前几题的位置考查,难度较低.
2.命题的热点依然会考查集合的运算,集合的基本关系的相关命题要注意.
3.常用逻辑用语考查的频率不多,且命题点分散,主要是充要条件的判断及含有量词的命题的否定交汇综合命题.
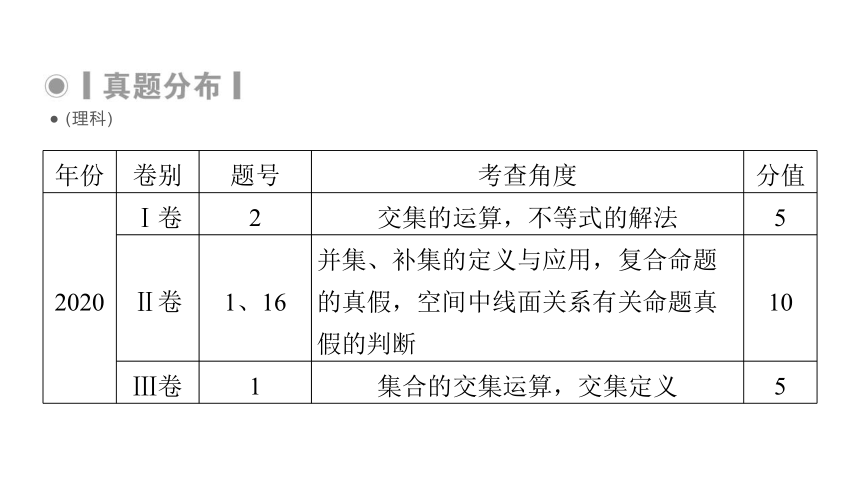
(理科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
2
交集的运算,不等式的解法
5
Ⅱ卷
1、16
并集、补集的定义与应用,复合命题的真假,空间中线面关系有关命题真假的判断
10
Ⅲ卷
1
集合的交集运算,交集定义
5
年份
卷别
题号
考查角度
分值
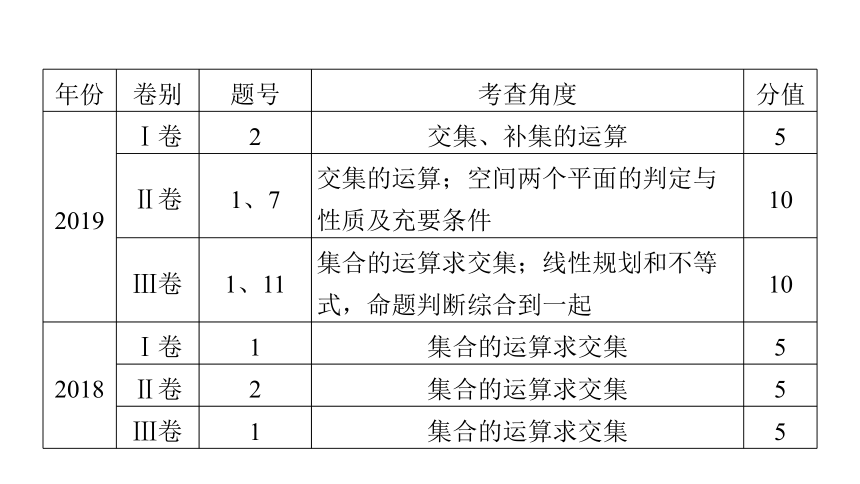
2019
Ⅰ卷
1
交集、二次不等式、韦恩图
5
Ⅱ卷
1、7
二次不等式、充要条件与面面平行
10
Ⅲ卷
1
交集、不等式
5
2018
Ⅰ卷
2
集合的补集与一元二次不等式
5
Ⅱ卷
2
集合元素个数的确定
5
Ⅲ卷
1
集合的交集与一元二次不等式
5
(文科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
1
利用一元二次不等式的解法求集合,集合的交运算
5
Ⅱ卷
1、16
绝对值不等式的解法,集合交集的定义;复合命题的真假,空间中线面关系有关命题真假的判断
10
Ⅲ卷
1
集合的交集运算,交集定义
5
年份
卷别
题号
考查角度
分值
2019
Ⅰ卷
2
交集、补集的运算
5
Ⅱ卷
1、7
交集的运算;空间两个平面的判定与性质及充要条件
10
Ⅲ卷
1、11
集合的运算求交集;线性规划和不等式,命题判断综合到一起
10
2018
Ⅰ卷
1
集合的运算求交集
5
Ⅱ卷
2
集合的运算求交集
5
Ⅲ卷
1
集合的运算求交集
5
02 考点分类 · 析重点
考点一 集合
(3)任何一个集合是它本身的子集,即A?A;空集只有一个子集,即它本身.
(4)含有n(n∈N*)个元素的集合有2n个子集,有(2n-1)个真子集,有(2n-2)个非空真子集.
2.集合的运算性质及重要结论
(1)A∪B=A?B?A,A∩B=A?A?B.
(2)A∩A=A,A∩?=?.
(3)A∪A=A,A∪?=A.
(4)A∩(?UA)=?,A∪(?UA)=U,?U(?UA)=A.
(5)A?B?A∩B=A?A∪B=B?(?UA)?(?UB)?A∩(?UB)=?.
1.(2020·青海省玉树州高三联考)已知集合M={-1,0,1},N={x|x=2a,a∈M},则集合M∪N= ( )
A.{-1,0,1} B.{-2,0,2}
C.{0} D.{-2,-1,0,1,2}
【解析】 因为N={x|x=2a,a∈M},M={-1,0,1},
所以N={-2,0,2},
所以M∪N={-2,-1,0,1,2},故选D.
D
2.(2020·陕西省汉中市质检)已知集合A={x|-1 A.{x|0 C.{1,2} D.{2,3,4}
【解析】 ∵B={x∈Z|x2-4x<0}={x∈Z|0 ∴B={1,2,3},
∵A={x|-1 ∴A∩B={1,2},故选C.
C
C
4.(2020·云南省昆明市月考)已知集合A={x∈N|x2≤1},集合B={x∈Z|-1≤x≤3},则图中阴影部分表示的集合为 ( )
A.[1,3] B.(1,3]
C.{-1,2,3} D.{-1,0,2,3}
【解析】 A={x∈N|x2≤1}={0,1},
B={-1,0,1,2,3},
阴影部分对应的集合为?BA,
则?BA={-1,2,3},故选C.
C
5.(2020·江苏省天一中学调研)设全集U={x|x<5,x∈N*},集合A={1,3},B={3,4},则?U(A∪B)=________.
【解析】 ∵A={1,3},B={3,4},
∴A∪B={1,3,4},
∵U={x|x<5,x∈N*}={1,2,3,4},
∴?U(A∪B)={2}.
{2}
6.(2020·武昌统考)已知集合A={x|log2(x-1)<1},B={x||x-a|<2},若A?B,则实数a的取值范围为__________.
[1,3]
7.(2020·江苏南京师大附中模拟)给定集合A,若对于任意a,b∈A,有a+b∈A,a-b∈A,则称集合A为闭集合.给出如下三个结论:
①集合A={-4,-2,0,2,4}为闭集合;
②集合A={n|n=3k,k∈Z}为闭集合;
③若集合A1,A2为闭集合,则A1∪A2为闭集合.
其中正确结论的序号是_____.
②
1.集合运算中的常用方法
(1)数轴法:若已知的集合是不等式的解集,用数轴法求解.
(2)图象法:若已知的集合是点集,用图象法求解.
(3)Venn图法:若已知的集合是抽象集合,用Venn图法求解.
2.规避误区
(1)在化简集合时易忽视元素的特定范围(如集合中x∈N,x∈Z等)致误.
(2)在解决含参数的集合问题时,要注意检验集合中元素的互异性,否则很可能会因为不满足“互异性”而导致解题错误.
1.四种命题的关系
(1)两个命题互为逆否命题,它们有相同的真假性.
(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.
2.全(特)称命题及其否定
(1)全称命题p:?x∈M,p(x).它的否定?p:?x0∈M,?p(x0).
(2)特称命题p:?x0∈M,p(x0).它的否定?p:?x∈M,?p(x).
考点二 命题及真假判断
C
2.(2020·吉林省重点中学联考)关于“a+b=4,则a,b至少有一个等于2”及其逆命题的说法正确的是 ( )
A.原命题为真,逆命题为假
B.原命题为假,逆命题为真
C.原命题与逆命题均为真命题
D.原命题与逆命题均为假命题
【解析】 若a=1.9,b=2.1,则a+b=4,故原命题为假;
若a=2,b=2.1,则a+b≠4,故其逆命题为假.故选D.
D
3.(2020·安徽省十四校联盟段考)下列命题中正确的是 ( )
A.?x0∈R,ex0≤
B.?x∈R,2x≥x2
C.若(?p)∧q是真命题,则p∨(?q)是假命题
D.1≥0是假命题
【解析】 ?x∈R,ex>0,故A错误;当x=3时,2x ∵(?p)∧q是真命题,∴p是假命题,q是真命题,
∴p∨(?q)是假命题,故C正确;选项D显然错误.故选C.
C
D
B
6.(2020·四川省成都七中一诊)命题“?x∈N,x2>1”的否定为_______________.
【解析】 全称命题“?x∈M,p(x)”的否定是存在性命题“?x∈M,?p(x)”,所以“?x∈N,x2>1”的否定是“?x∈N,x2≤1”.
?x∈N,x2≤1
(-∞,1]
1.命题真假的判定方法
(1)一般命题p的真假由涉及的相关知识辨别.
(2)四种命题真假的判断:一个命题和它的逆否命题同真假,而互为逆命题和互为否命题的两个命题的真假无此规律.
(3)形如p∨q,p∧q,?p命题的真假根据p,q的真假与联结词的含义判定.
2.全称命题与特称命题真假的判定
(1)全称命题:要判定一个全称命题是真命题,必须对限定集合M中的每一个元素x验证p(x)成立,要判定其为假命题时,只需举出一个反例即可.
(2)特称命题:要判定一个特称命题为真命题,只要在限定集合M中至少能找到一个元素x0,使得p(x0)成立即可;否则,这一特称命题就是假命题.
1.若p?q,则p是q的充分条件,q是p的必要条件.
2.若p?q,则p,q互为充要条件.
考点三 充要条件
1.(2020·柯桥区模拟)已知a,b∈R,则“a2>b2”是“a>|b|”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】 由a>|b|?a2>b2;反之不成立,例如:取a=-2,b=-1.
∴“a2>b2”是“a>|b|”的必要不充分条件.故选B.
B
2.(2020·宣城二模)若直线m,n表示两条不同的直线,则m∥n的充要条件是 ( )
A.存在直线l,使m⊥l,n⊥l
B.存在平面α,使m⊥α,n⊥α
C.存在平面α,使m∥α,n∥α
D.存在直线l,使m,n与直线l所成的角都是45°
B
【解析】 A.存在直线l,使m⊥l,n⊥l,则直线m,n可能平行、相交或异面,因此不正确.
B.存在平面α,使m⊥α,n⊥α?m∥n.
C.存在平面α,使m∥α,n∥α,则直线m,n可能平行、相交或异面直线,因此不正确.
D.存在直线l,使m,n与直线l所成的角都是45°,则m与n可能相交、平行或为异面直线.故选B.
3.(2020·海淀区校级一模)数列{an}的通项公式为an=|n-c|(n∈N*).则“c<2”是“{an}为递增数列”的什么条件 ( )
A.必要而不充分 B.充要
C.充分而不必要 D.即不充分也不必要
A
A
5.(2020·崇川区校级模拟)设命题p:x≤4;命题q:x2-5x+4≤0,那么p是q的_____________条件.(填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
【解析】 命题q:x2-5x+4≤0,解得:1≤x≤4.
∴q?p,反之不成立.
那么p是q的必要不充分条件.
必要不充分
6.(2020·南通模拟)已知命题p:-1<x-a<1,命题q:(x-4)(8-x)>0,若p是q的充分不必要条件,则实数a的取值范围是__________.
[5,7]
03 易错清零 · 免失误
已知全集U={1,3,x3+3x2+2x}和它的子集A={1,|2x-1|},如果集合A在U中的补集为{0},求实数x的值.
典例1
1.因忽视集合中元素的互异性而致误
【解析】 因为U={1,3,x3+3x2+2x},且集合A在U中的补集为{0},
所以0∈U,x3+3x2+2x=0,
解得x1=0,x2=-1,x3=-2.
设P={y|y=x2,x∈R},Q={y|y=2-|x|,x∈R},求P∩Q.
典例2
2.忽视代表元素而致误
【剖析】 上述解法混淆了集合的代表元素,本题中两个集合中的代表元素是y,而不是点的坐标.
【正解】 因为P={y|y=x2,x∈R}={y|y≥0},Q={y|y=2-|x|,x∈R}={y|y≤2},所以P∩Q={y|y≥0}∩{y|y≤2}={y|0≤y≤2}.
(2020·宜昌一中第一次月考)集合A={-1,2},B={x|ax-2=0},若B?A,则由实数a的取值组成的集合为 ( )
A.{-2} B.{1}
C.{-2,1} D.{-2,1,0}
典例3
3.遗忘空集或区间端点致误
D
【剖析】 上述解法的错误在于忽略了B=?,因为空集是任何集合的子集.
空集作为一种特殊的集合,在集合的相关问题中,稍不注意就会出现错误.在解答含有参数的集合问题时,遇到以下三种情形不能忽略空集:①B?A;②B∩A=B;③B∪A=A.如果遗忘了对空集的讨论,就会容易导致解题错误或解题不全面.
(2020·衡阳八中第一次月考)已知集合A={x|y=log2(x2-4)},B={x|x2-3mx+2m2<0(m>0)},若B?A,则实数m的取值范围为 ( )
A.(4,+∞) B.[4,+∞)
C.(2,+∞) D.[2,+∞)
典例4
D
【解析】 由x2-4 >0,得x<-2或x>2,
则A=(-∞,-2)∪(2,+∞).
由x2-3mx+2m2<0(m>0),得m0),
则B=(m,2m).
由B?A可知m≥2,
所以实数m的取值范围为[2,+∞).故选D.
【剖析】 用数轴分析法求解集合的包含关系时,要注意“端点”能否取到.本题中,注意到集合A,B都是开区间,因此m可以取到2,若遗漏掉m =2,则会导致求出的符合题意的实数m的取值不完整,就会出现错解.
【错解】 C
典例5
4.混淆充分条件与必要条件的关系致误
A
【错解】 A
典例6
5.对“或、且、非”理解不准致误
B
【正解】 在平面直角坐标系中作出y=2x与y=x2的图象,如图1所示,结合图可知当x∈(2,4)时,2x 在平面直角坐标系中作出
y=x3与y=1-x2的图象,如图2
所示,结合图可知y=x3与
y=1-x2的图象有交点,可知
q为真命题.
所以(?p)∧q为真命题.故选B.
04 真题回放 · 悟高考
1.(2019·全国卷Ⅰ)已知集合M={x|-4<x<2},N={x|x2-x-6<0},则M∩N= ( )
A.{x|-4<x<3} B.{x|-4<x<-2}
C.{x|-2<x<2} D.{x|2<x<3}
【解析】 ∵M={x|-4<x<2},N={x|x2-x-6<0}={x|-2<x<3},∴M∩N={x|-2<x<2}.故选C.
C
2.(2019·全国卷Ⅱ)设集合A={x|x2-5x+6>0},B={x|x-1<0},则A∩B= ( )
A.(-∞,1) B.(-2,1)
C.(-3,-1) D.(3,+∞)
【解析】 根据题意,A={x|x2-5x+6>0}={x|x>3或x<2},B={x|x-1<0}={x|x<1},则A∩B={x|x<1}=(-∞,1),故选A.
A
3.(2018·全国卷Ⅰ)已知集合A={x|x2-x-2>0},则?RA= ( )
A.{x|-1 C.{x|x<-1}∪{x|x>2} D.{x|x≤-1}∪{x|x≥2}
【解析】 ∵x2-x-2>0,∴(x-2)(x+1)>0,∴x>2或x<-1,即A={x|x>2或x<-1}.在数轴上表示出集合A,如图所示.
由图可得?RA={x|-1≤x≤2}.故选B.
B
4.(2018·全国卷Ⅱ)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为 ( )
A.9 B.8
C.5 D.4
【解析】 将满足x2+y2≤3的整数x,y全部列举出来,即(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),共有9个.故选A.
A
A
【解析】 法一:画出可行域如图中阴影部分所示.
目标函数z=2x+y是一条平行移动的直线,且z的几何意义是直线z=2x+y的纵截距.
显然,直线过点A(2,4)时,zmin=2×2+4=8,
即z=2x+y≥8.∴2x+y∈[8,+∞).
由此得命题p:?(x,y)∈D,2x+y≥9正确;
命题q:?(x,y)∈D,2x+y≤12不正确.
∴①③真,②④假.故选A.
6.(2020·全国卷Ⅱ卷)已知集合U={-2,-1,0,1,2,3},A={-1,0,1},B={1,2},则?U(A∪B)= ( )
A.{-2,3} B.{-2,2,3}
C.{-2,-1,0,3} D.{-2,-1,0,2,3}
【解析】 由题意可得:A∪B={-1,0,1,2},则?U(A∪B)={-2,3}.
A
7.(2020·全国卷Ⅰ卷)设集合A={x|x2–4≤0},B={x|2x+a≤0},且A∩B={x|–2≤x≤1},则a= ( )
A.-4 B.-2
C.2 D.4
B
8.(2020·全国卷Ⅱ卷)已知集合A={1,2,3,5,7,11},B={x|3 A.2 B.3
C.4 D.5
【解析】 由题意,A∩B={5,7,11},故A∩B中元素的个数为3.
B
方法篇?素养形成(文理)
第2讲 集合与常用逻辑用语(文理)
1 解题策略 · 明方向
2 考点分类 · 析重点
3 易错清零 · 免失误
4 真题回放 · 悟高考
5 预测演练 · 巧押题
1.本部分作为高考必考内容,仍会以选择题的形式在前几题的位置考查,难度较低.
2.命题的热点依然会考查集合的运算,集合的基本关系的相关命题要注意.
3.常用逻辑用语考查的频率不多,且命题点分散,主要是充要条件的判断及含有量词的命题的否定交汇综合命题.
(理科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
2
交集的运算,不等式的解法
5
Ⅱ卷
1、16
并集、补集的定义与应用,复合命题的真假,空间中线面关系有关命题真假的判断
10
Ⅲ卷
1
集合的交集运算,交集定义
5
年份
卷别
题号
考查角度
分值
2019
Ⅰ卷
1
交集、二次不等式、韦恩图
5
Ⅱ卷
1、7
二次不等式、充要条件与面面平行
10
Ⅲ卷
1
交集、不等式
5
2018
Ⅰ卷
2
集合的补集与一元二次不等式
5
Ⅱ卷
2
集合元素个数的确定
5
Ⅲ卷
1
集合的交集与一元二次不等式
5
(文科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
1
利用一元二次不等式的解法求集合,集合的交运算
5
Ⅱ卷
1、16
绝对值不等式的解法,集合交集的定义;复合命题的真假,空间中线面关系有关命题真假的判断
10
Ⅲ卷
1
集合的交集运算,交集定义
5
年份
卷别
题号
考查角度
分值
2019
Ⅰ卷
2
交集、补集的运算
5
Ⅱ卷
1、7
交集的运算;空间两个平面的判定与性质及充要条件
10
Ⅲ卷
1、11
集合的运算求交集;线性规划和不等式,命题判断综合到一起
10
2018
Ⅰ卷
1
集合的运算求交集
5
Ⅱ卷
2
集合的运算求交集
5
Ⅲ卷
1
集合的运算求交集
5
02 考点分类 · 析重点
考点一 集合
(3)任何一个集合是它本身的子集,即A?A;空集只有一个子集,即它本身.
(4)含有n(n∈N*)个元素的集合有2n个子集,有(2n-1)个真子集,有(2n-2)个非空真子集.
2.集合的运算性质及重要结论
(1)A∪B=A?B?A,A∩B=A?A?B.
(2)A∩A=A,A∩?=?.
(3)A∪A=A,A∪?=A.
(4)A∩(?UA)=?,A∪(?UA)=U,?U(?UA)=A.
(5)A?B?A∩B=A?A∪B=B?(?UA)?(?UB)?A∩(?UB)=?.
1.(2020·青海省玉树州高三联考)已知集合M={-1,0,1},N={x|x=2a,a∈M},则集合M∪N= ( )
A.{-1,0,1} B.{-2,0,2}
C.{0} D.{-2,-1,0,1,2}
【解析】 因为N={x|x=2a,a∈M},M={-1,0,1},
所以N={-2,0,2},
所以M∪N={-2,-1,0,1,2},故选D.
D
2.(2020·陕西省汉中市质检)已知集合A={x|-1
【解析】 ∵B={x∈Z|x2-4x<0}={x∈Z|0
∵A={x|-1
C
C
4.(2020·云南省昆明市月考)已知集合A={x∈N|x2≤1},集合B={x∈Z|-1≤x≤3},则图中阴影部分表示的集合为 ( )
A.[1,3] B.(1,3]
C.{-1,2,3} D.{-1,0,2,3}
【解析】 A={x∈N|x2≤1}={0,1},
B={-1,0,1,2,3},
阴影部分对应的集合为?BA,
则?BA={-1,2,3},故选C.
C
5.(2020·江苏省天一中学调研)设全集U={x|x<5,x∈N*},集合A={1,3},B={3,4},则?U(A∪B)=________.
【解析】 ∵A={1,3},B={3,4},
∴A∪B={1,3,4},
∵U={x|x<5,x∈N*}={1,2,3,4},
∴?U(A∪B)={2}.
{2}
6.(2020·武昌统考)已知集合A={x|log2(x-1)<1},B={x||x-a|<2},若A?B,则实数a的取值范围为__________.
[1,3]
7.(2020·江苏南京师大附中模拟)给定集合A,若对于任意a,b∈A,有a+b∈A,a-b∈A,则称集合A为闭集合.给出如下三个结论:
①集合A={-4,-2,0,2,4}为闭集合;
②集合A={n|n=3k,k∈Z}为闭集合;
③若集合A1,A2为闭集合,则A1∪A2为闭集合.
其中正确结论的序号是_____.
②
1.集合运算中的常用方法
(1)数轴法:若已知的集合是不等式的解集,用数轴法求解.
(2)图象法:若已知的集合是点集,用图象法求解.
(3)Venn图法:若已知的集合是抽象集合,用Venn图法求解.
2.规避误区
(1)在化简集合时易忽视元素的特定范围(如集合中x∈N,x∈Z等)致误.
(2)在解决含参数的集合问题时,要注意检验集合中元素的互异性,否则很可能会因为不满足“互异性”而导致解题错误.
1.四种命题的关系
(1)两个命题互为逆否命题,它们有相同的真假性.
(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.
2.全(特)称命题及其否定
(1)全称命题p:?x∈M,p(x).它的否定?p:?x0∈M,?p(x0).
(2)特称命题p:?x0∈M,p(x0).它的否定?p:?x∈M,?p(x).
考点二 命题及真假判断
C
2.(2020·吉林省重点中学联考)关于“a+b=4,则a,b至少有一个等于2”及其逆命题的说法正确的是 ( )
A.原命题为真,逆命题为假
B.原命题为假,逆命题为真
C.原命题与逆命题均为真命题
D.原命题与逆命题均为假命题
【解析】 若a=1.9,b=2.1,则a+b=4,故原命题为假;
若a=2,b=2.1,则a+b≠4,故其逆命题为假.故选D.
D
3.(2020·安徽省十四校联盟段考)下列命题中正确的是 ( )
A.?x0∈R,ex0≤
B.?x∈R,2x≥x2
C.若(?p)∧q是真命题,则p∨(?q)是假命题
D.1≥0是假命题
【解析】 ?x∈R,ex>0,故A错误;当x=3时,2x
∴p∨(?q)是假命题,故C正确;选项D显然错误.故选C.
C
D
B
6.(2020·四川省成都七中一诊)命题“?x∈N,x2>1”的否定为_______________.
【解析】 全称命题“?x∈M,p(x)”的否定是存在性命题“?x∈M,?p(x)”,所以“?x∈N,x2>1”的否定是“?x∈N,x2≤1”.
?x∈N,x2≤1
(-∞,1]
1.命题真假的判定方法
(1)一般命题p的真假由涉及的相关知识辨别.
(2)四种命题真假的判断:一个命题和它的逆否命题同真假,而互为逆命题和互为否命题的两个命题的真假无此规律.
(3)形如p∨q,p∧q,?p命题的真假根据p,q的真假与联结词的含义判定.
2.全称命题与特称命题真假的判定
(1)全称命题:要判定一个全称命题是真命题,必须对限定集合M中的每一个元素x验证p(x)成立,要判定其为假命题时,只需举出一个反例即可.
(2)特称命题:要判定一个特称命题为真命题,只要在限定集合M中至少能找到一个元素x0,使得p(x0)成立即可;否则,这一特称命题就是假命题.
1.若p?q,则p是q的充分条件,q是p的必要条件.
2.若p?q,则p,q互为充要条件.
考点三 充要条件
1.(2020·柯桥区模拟)已知a,b∈R,则“a2>b2”是“a>|b|”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】 由a>|b|?a2>b2;反之不成立,例如:取a=-2,b=-1.
∴“a2>b2”是“a>|b|”的必要不充分条件.故选B.
B
2.(2020·宣城二模)若直线m,n表示两条不同的直线,则m∥n的充要条件是 ( )
A.存在直线l,使m⊥l,n⊥l
B.存在平面α,使m⊥α,n⊥α
C.存在平面α,使m∥α,n∥α
D.存在直线l,使m,n与直线l所成的角都是45°
B
【解析】 A.存在直线l,使m⊥l,n⊥l,则直线m,n可能平行、相交或异面,因此不正确.
B.存在平面α,使m⊥α,n⊥α?m∥n.
C.存在平面α,使m∥α,n∥α,则直线m,n可能平行、相交或异面直线,因此不正确.
D.存在直线l,使m,n与直线l所成的角都是45°,则m与n可能相交、平行或为异面直线.故选B.
3.(2020·海淀区校级一模)数列{an}的通项公式为an=|n-c|(n∈N*).则“c<2”是“{an}为递增数列”的什么条件 ( )
A.必要而不充分 B.充要
C.充分而不必要 D.即不充分也不必要
A
A
5.(2020·崇川区校级模拟)设命题p:x≤4;命题q:x2-5x+4≤0,那么p是q的_____________条件.(填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
【解析】 命题q:x2-5x+4≤0,解得:1≤x≤4.
∴q?p,反之不成立.
那么p是q的必要不充分条件.
必要不充分
6.(2020·南通模拟)已知命题p:-1<x-a<1,命题q:(x-4)(8-x)>0,若p是q的充分不必要条件,则实数a的取值范围是__________.
[5,7]
03 易错清零 · 免失误
已知全集U={1,3,x3+3x2+2x}和它的子集A={1,|2x-1|},如果集合A在U中的补集为{0},求实数x的值.
典例1
1.因忽视集合中元素的互异性而致误
【解析】 因为U={1,3,x3+3x2+2x},且集合A在U中的补集为{0},
所以0∈U,x3+3x2+2x=0,
解得x1=0,x2=-1,x3=-2.
设P={y|y=x2,x∈R},Q={y|y=2-|x|,x∈R},求P∩Q.
典例2
2.忽视代表元素而致误
【剖析】 上述解法混淆了集合的代表元素,本题中两个集合中的代表元素是y,而不是点的坐标.
【正解】 因为P={y|y=x2,x∈R}={y|y≥0},Q={y|y=2-|x|,x∈R}={y|y≤2},所以P∩Q={y|y≥0}∩{y|y≤2}={y|0≤y≤2}.
(2020·宜昌一中第一次月考)集合A={-1,2},B={x|ax-2=0},若B?A,则由实数a的取值组成的集合为 ( )
A.{-2} B.{1}
C.{-2,1} D.{-2,1,0}
典例3
3.遗忘空集或区间端点致误
D
【剖析】 上述解法的错误在于忽略了B=?,因为空集是任何集合的子集.
空集作为一种特殊的集合,在集合的相关问题中,稍不注意就会出现错误.在解答含有参数的集合问题时,遇到以下三种情形不能忽略空集:①B?A;②B∩A=B;③B∪A=A.如果遗忘了对空集的讨论,就会容易导致解题错误或解题不全面.
(2020·衡阳八中第一次月考)已知集合A={x|y=log2(x2-4)},B={x|x2-3mx+2m2<0(m>0)},若B?A,则实数m的取值范围为 ( )
A.(4,+∞) B.[4,+∞)
C.(2,+∞) D.[2,+∞)
典例4
D
【解析】 由x2-4 >0,得x<-2或x>2,
则A=(-∞,-2)∪(2,+∞).
由x2-3mx+2m2<0(m>0),得m
则B=(m,2m).
由B?A可知m≥2,
所以实数m的取值范围为[2,+∞).故选D.
【剖析】 用数轴分析法求解集合的包含关系时,要注意“端点”能否取到.本题中,注意到集合A,B都是开区间,因此m可以取到2,若遗漏掉m =2,则会导致求出的符合题意的实数m的取值不完整,就会出现错解.
【错解】 C
典例5
4.混淆充分条件与必要条件的关系致误
A
【错解】 A
典例6
5.对“或、且、非”理解不准致误
B
【正解】 在平面直角坐标系中作出y=2x与y=x2的图象,如图1所示,结合图可知当x∈(2,4)时,2x
y=x3与y=1-x2的图象,如图2
所示,结合图可知y=x3与
y=1-x2的图象有交点,可知
q为真命题.
所以(?p)∧q为真命题.故选B.
04 真题回放 · 悟高考
1.(2019·全国卷Ⅰ)已知集合M={x|-4<x<2},N={x|x2-x-6<0},则M∩N= ( )
A.{x|-4<x<3} B.{x|-4<x<-2}
C.{x|-2<x<2} D.{x|2<x<3}
【解析】 ∵M={x|-4<x<2},N={x|x2-x-6<0}={x|-2<x<3},∴M∩N={x|-2<x<2}.故选C.
C
2.(2019·全国卷Ⅱ)设集合A={x|x2-5x+6>0},B={x|x-1<0},则A∩B= ( )
A.(-∞,1) B.(-2,1)
C.(-3,-1) D.(3,+∞)
【解析】 根据题意,A={x|x2-5x+6>0}={x|x>3或x<2},B={x|x-1<0}={x|x<1},则A∩B={x|x<1}=(-∞,1),故选A.
A
3.(2018·全国卷Ⅰ)已知集合A={x|x2-x-2>0},则?RA= ( )
A.{x|-1
【解析】 ∵x2-x-2>0,∴(x-2)(x+1)>0,∴x>2或x<-1,即A={x|x>2或x<-1}.在数轴上表示出集合A,如图所示.
由图可得?RA={x|-1≤x≤2}.故选B.
B
4.(2018·全国卷Ⅱ)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为 ( )
A.9 B.8
C.5 D.4
【解析】 将满足x2+y2≤3的整数x,y全部列举出来,即(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),共有9个.故选A.
A
A
【解析】 法一:画出可行域如图中阴影部分所示.
目标函数z=2x+y是一条平行移动的直线,且z的几何意义是直线z=2x+y的纵截距.
显然,直线过点A(2,4)时,zmin=2×2+4=8,
即z=2x+y≥8.∴2x+y∈[8,+∞).
由此得命题p:?(x,y)∈D,2x+y≥9正确;
命题q:?(x,y)∈D,2x+y≤12不正确.
∴①③真,②④假.故选A.
6.(2020·全国卷Ⅱ卷)已知集合U={-2,-1,0,1,2,3},A={-1,0,1},B={1,2},则?U(A∪B)= ( )
A.{-2,3} B.{-2,2,3}
C.{-2,-1,0,3} D.{-2,-1,0,2,3}
【解析】 由题意可得:A∪B={-1,0,1,2},则?U(A∪B)={-2,3}.
A
7.(2020·全国卷Ⅰ卷)设集合A={x|x2–4≤0},B={x|2x+a≤0},且A∩B={x|–2≤x≤1},则a= ( )
A.-4 B.-2
C.2 D.4
B
8.(2020·全国卷Ⅱ卷)已知集合A={1,2,3,5,7,11},B={x|3
C.4 D.5
【解析】 由题意,A∩B={5,7,11},故A∩B中元素的个数为3.
B
同课章节目录
