第1部分 第4讲不等式、算法与推理-2021届高三高考数学二轮复习课件(99张PPT)
文档属性
| 名称 | 第1部分 第4讲不等式、算法与推理-2021届高三高考数学二轮复习课件(99张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 21:26:53 | ||
图片预览











文档简介
第一部分
方法篇?素养形成(文理)
第4讲 不等式、算法与推理(文理)
1 解题策略 · 明方向
2 考点分类 · 析重点
3 易错清零 · 免失误
4 真题回放 · 悟高考
5 预测演练 · 巧押题
1.高考中主要考查求程序框图中的执行结果和确定控制条件.
2.在高考中主要以客观题形式考查不等式的性质和一元二次不等式的解法.
3.以画二元一次不等式(组)表示的平面区域、目标函数最值的求法为主.
4.利用基本不等式求最值,题型多样,突出“小而巧”的特点.
(理科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
2、13
二元一次不等式的解法;线性规划求最值
10
Ⅱ卷
8、17(2)
基本不等式应用
10
Ⅲ卷
13
线性规划求最值
5
年份
卷别
题号
考查角度
分值
2019
Ⅰ卷
1、3、4、8
不等式比较大小推理、框图
20
Ⅱ卷
6
不等式的性质
5
Ⅲ卷
1、9
二次不等式的求解、程序框图
10
2018
Ⅰ卷
2、3、13
集合补集、程序框图、一元二次不等式的解集、线性规划
15
Ⅱ卷
7、14
程序框图、线性规划
10
Ⅲ卷
1、12
一元一次不等式的解集、集合运算、不等式的性质、对数运算
10
(文科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
1、9、13
利用一元二次不等式的解法求集合;程序框图的算法功能;简单线性规划求最值
15
Ⅱ卷
7、15
程序框图的应用;简单线性规划求最值
10
Ⅲ卷
13
简单线性规划求线性目标函数的最大值
5
年份
卷别
题号
考查角度
分值
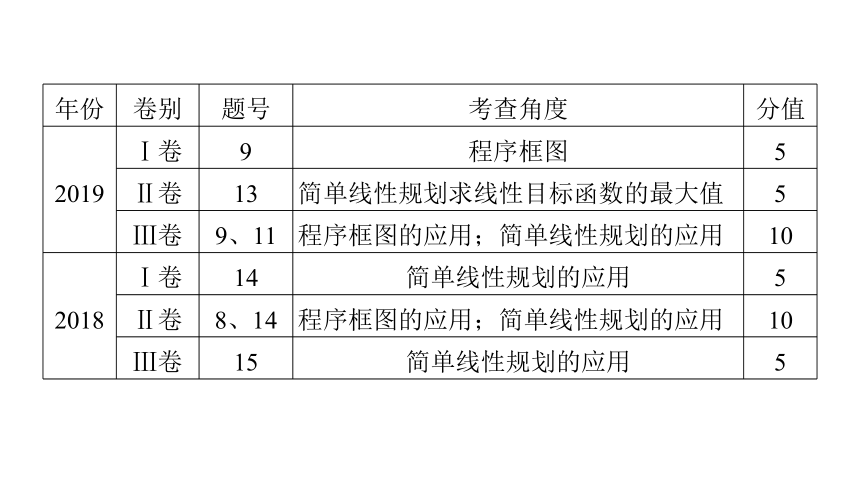
2019
Ⅰ卷
9
程序框图
5
Ⅱ卷
13
简单线性规划求线性目标函数的最大值
5
Ⅲ卷
9、11
程序框图的应用;简单线性规划的应用
10
2018
Ⅰ卷
14
简单线性规划的应用
5
Ⅱ卷
8、14
程序框图的应用;简单线性规划的应用
10
Ⅲ卷
15
简单线性规划的应用
5
02 考点分类 · 析重点
1.一元二次不等式的解法
先化为一般形式ax2+bx+c>0(a≠0),再求相应一元二次方程ax2+bx+c=0(a≠0)的根,最后根据相应二次函数图象与x轴的位置关系,确定一元二次不等式的解集.
考点一 不等式的性质及解法
D
B
B
4.(2020·重庆朝阳中学期中)关于x的不等式x2-(m+1)x+(m+1)≥0对一切x∈R恒成立,则实数m的取值范围为 ( )
A.[-3,1] B.[-3,3]
C.[-1,1] D.[-1,3]
【解析】 ∵关于x的不等式x2-(m+1)x+(m+1)≥0对一切x∈R恒成立,∴Δ=(m+1)2-4(m+1)=(m+1)(m-3)≤0,
解得-1≤m≤3,∴实数m的取值范围为[-1,3].故选D.
D
不等式的求解技巧
(1)对于和函数有关的不等式,可利用函数的单调性进行转化.
(2)求解一元二次不等式的步骤:
第一步,二次项系数化为正数;
第二步,解相应的一元二次方程;
第三步,若有两个不相等的实根,则利用“大于在两边,小于夹中间”得不等式的解集.
(3)含参数的不等式的求解,要对参数进行分类讨论.
1.线性规划
(1)①不等式y>kx+b表示直线y=kx+b上方区域;
②等式y=kx+b表示直线y=kx+b上的区域;
③不等式y ④x>a表直线x=a右侧区域,x考点二 线性规划和基本不等式
(2)线性目标函数z=ax+by,作可行域与直线l:ax+by=0,并平移直线l
①b>0时上移l、z增大,下移l、z减小,即“上增下减”;
②b<0时“上减下增”.
D
B
B
B
考向2 基本不等式
5.(2020·吉林省重点中学联考)若实数x,y满足x+y=8,则x2+y2的最小值是 ( )
A.8 B.32
C.16 D.4
B
A
8
8.(2020·江苏省八校联考)已知实数a,b满足4a2-5ab+4b2=9,则a+b最大值为______.
两种循环结构的特点
直到型循环结构:在执行了一次循环体后,对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.
当型循环结构:在每次执行循环体前,对条件进行判断,当条件满足时,执行循环体,否则终止循环.
考点三 算法与程序框图
考向1 直接循环计算
1.(2020·四川省成都七中一诊)执行如图所示的程序框图,输出的S值为 ( )
A.3 B.-6
C.10 D.-15
【解析】 根据程序框图可知S=-12+22-32+42=10,故选C.
C
C
考向2 完善判断框
3.(2020·四川省成都七中模拟)按照如图的程序框图执行,若输出结果为15,则M处条件为 ( )
A.k≥16?
B.k<8?
C.k<16?
D.k≥8?
A
【解析】 根据题中所给的程序框图,可以确定该题要求的是S=1+2+4+8+...,
对应的正好是以1为首项,以2为公比的等比数列,
该数列的前4项和正好是15,结合题中所给的条件,一一试过,可知当k≥16时,退出循环,故选A.
解答程序框图(流程图)问题的方法
(1)首先要读懂程序框图,要熟练掌握程序框图的三种基本结构,特别是循环结构,在累加求和、累乘求积、多次输入等有规律的科学计算中,都有循环结构.
(2)准确把握控制循环的变量,变量的初值和循环条件,弄清在哪一步结束循环;弄清循环体和输入条件、输出结果.
(3)对于循环次数比较少的可逐步写出,对于循环次数较多的可先依次列出前几次循环结果,找出规律.
1.合情推理
合情推理是根据已有的事实和正确的结论推测某些结果的推理过程.通过观察特例,形成猜想,严格论证,是发现(提出)问题,解决问题的常用方法.归纳、类比推理是根据个别事实,通过分析提出猜想的推理,其结论可能是错误的.
考点四 推理与证明
而演绎推理是由一般性原理出发,推出某个特殊情况下的结论,其结论是准确的.在进行类比推理时要尽量从本质上类比,不要被表面现象所迷惑,犯机械类比的错误.类比除了发现结论外,还可以发现证明结论的思路和方法.要善于观察和总结,养成归纳、类比、联想的习惯.
2.反证法
有些问题如果从正面求解繁琐或无法求解时,则可从其反面进行思考,通过否定结论的反面来肯定结论正确,这就是“正难则反”的思路.用反证法证题推出矛盾主要有下列情形:
①与已知条件矛盾;
②与公理、定理、定义及性质矛盾;
③与假设矛盾.
宜用反证法证明的题型:
①易导出与已知矛盾的命题;
②否定性命题;
③唯一性命题;
④至少、至多型命题;
⑤某些基本定理;
⑥必然性命题.
【答案】 C
2.观察下列等式:
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
……
照此规律,第n个等式可为
?
_________________________________________________.
C
考向3 直接证明与间接证明
4.(2020·潍坊检测)用反证法证明命题:“若a∈R,则函数y=x3+ax+b至少有一个零点”时,要做的假设是 ( )
A.函数y=x3+ax+b没有零点
B.函数y=x3+ax+b至多有一个零点
C.函数y=x3+ax+b至多有两个零点
D.函数y=x3+ax+b恰好有一个零点
【解析】 根据反证法的定义,可知“若a∈R,则函数y=x3+ax+b至少有一个零点”的反设应为“若a∈R,则函数y=x3+ax+b没有零点”.故选A.
A
C
1.破解归纳推理题的思维三步骤
(1)发现共性:通过观察特例发现某些相似性(特例的共性或一般规律);
(2)归纳推理:把这种相似性推广为一个明确表述的一般命题(猜想);
(3)检验结论:对所得的一般性命题进行检验,一般地,“求同存异”“逐步细化”“先粗后精”是求解由特殊结论推广到一般结论型创新题的基本技巧.
2.破解类比推理题的三个关键
(1)会定类,即找出两类对象之间可以确切表述的相似特征;
(2)会推测,即用一类事物的性质去推测另一类事物的性质,得出一个明确的猜想;
(3)会检验,即检验猜想的正确性.要将类比推理运用正确.
03 易错清零 · 免失误
(2020·青羊期中)若不等式ax2+2ax-1<0的解集为R,则a的取值范围是___________.
典例1
1.解含参数的不等式时不知道如何对参数分类讨论
(-1,0]
【剖析】 上述解法的错误是忽略了对a的讨论,若在二次不等式中二次项的系数中含有参数,就要讨论二次项系数等于0和不等于0两种情况.
典例2
2.忽略应用基本不等式的前提条件致误
D
(2020·江西名校第一次联考)执行如图所示的程序框图,若输出的S=1 320,则判断框中可填入 ( )
A.k≤12?
B.k≤11?
C.k≤10?
D.k≤9?
典例3
3.错判程序框图中判断框内的条件
D
【解析】 初始值k=12,S=1,
执行框图如下.
S=1,若满足判断框内的条件,则输出1,与已知不符,故判断框内的条件不成立,
S=1×12=12,k=12-1=11;
此时若满足判断框内的条件,则输出12,与已知不符,故判断框内的条件不成立,
S=12×11=132,k=11-1=10;
此时若满足判断框内的条件,则输出132,与已知不符,故判断框内的条件不成立,
S=132×10=1 320,k=10-1=9;
此时若满足判断框内的条件,则输出1 320,与已知相符,故此时判断框内的条件成立.
此时k=9,结合选项可知只有D项满足,故选D.
【剖析】 (1)该题易出现的问题主要是忽视输出结果与判断框内条件的对应,导致判断错误.
(2)解决此类问题需要注意两个方面.一是整体把握程序框图的功能.显然本题中的程序框图的功能是计算12×11×…的值,输出的结果1 320=12×11×10,故当k=10时,仍要进入循环体进行运算,当k=9时,跳出循环体,输出结果,二是要注意判断框内条件的形式.“等号”会影响计算的次数与输出的结果,如该题,若判断框内的条件不带等号,即改为“k<9?”,则需要再进行一次运算,输出的结果就是1 320×9了,事实上,该题中判断框内还可以填入“k<10?”.
(2020·湖南长郡中学模拟)已知从1开始的连续奇数按照蛇形排列形成宝塔形数表,第一行为1,第二行为3,5,第三行为11,9,7,第四行为13,15,17,19,…,如图所示,将在宝塔形数表中位于第i行,第j列的数记为aij,比如a32=9,a42=15,a54=23,若aij=2 019,则i+j= ( )
A.72 B.71
C.66 D.65
典例4
4.归纳不当致误
B
【剖析】 该题易出现的问题主要有以下几个方面:一是不能准确确定2 019在宝塔形数表中的位置,导致判断错误;二是在判断2 019所在行时,不能正确归纳出每行中的奇数的个数,从而导致求得的前i行的奇数个数之和出错,行数定位错误;三是在确定2 019所在列时,不能正确利用其所在行的首位奇数和排列方向,导致列数定位出错,该题根据已如归纳第i行奇数的个数以及第i行奇数的排列顺序是关键.
04 真题回放 · 悟高考
C
A
B
【解析】 把各循环变量在各次循环中的值用表格表示如下.
4.(2019·全国Ⅱ理6)若a>b,则 ( )
A.ln (a-b)>0 B.3a<3b
C.a3-b3>0 D.|a|>|b|
C
5.(2019·全国卷Ⅱ)在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测.
甲:我的成绩比乙高.
乙:丙的成绩比我和甲的都高.
丙:我的成绩比乙高.
成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为 ( )
A.甲、乙、丙 B.乙、甲、丙
C.丙、乙、甲 D.甲、丙、乙
A
【解析】 若甲预测正确,则乙、丙预测错误,则甲比乙成绩高,丙比乙成绩低,故3人成绩由高到低依次为甲,乙,丙;若乙预测正确,则丙预测也正确,不符合题意;若丙预测正确,则甲必预测错误,丙比乙的成绩高,乙比甲成绩高,即丙比甲,乙成绩都高,即乙预测正确,不符合题意.故选A.
6.(2020·全国卷Ⅰ卷)执行下面的程序框图,则输出的n= ( )
A.17
B.19
C.21
D.23
C
7.(2020·全国卷Ⅱ卷)执行下面的程序框图,若输入的k=0,a=0,则输出的k为 ( )
A.2
B.3
C.4
D.5
C
【解析】 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出的k值
模拟程序的运行过程
k=0,a=0
第1次循环,a=2×0+1=1,k=0+1=1,1>10为否
第2次循环,a=2×1+1=3,k=1+1=2,3>10为否
第3次循环,a=2×3+1=7,k=2+1=3,7>10为否
第4次循环,a=2×7+1=15,k=3+1=4,15>10为是
退出循环
输出k=4.
故选C.
1
【解析】 绘制不等式组表示的平面区域如图所示,
7
【解析】 不等式组所表示的可行域如图:
方法篇?素养形成(文理)
第4讲 不等式、算法与推理(文理)
1 解题策略 · 明方向
2 考点分类 · 析重点
3 易错清零 · 免失误
4 真题回放 · 悟高考
5 预测演练 · 巧押题
1.高考中主要考查求程序框图中的执行结果和确定控制条件.
2.在高考中主要以客观题形式考查不等式的性质和一元二次不等式的解法.
3.以画二元一次不等式(组)表示的平面区域、目标函数最值的求法为主.
4.利用基本不等式求最值,题型多样,突出“小而巧”的特点.
(理科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
2、13
二元一次不等式的解法;线性规划求最值
10
Ⅱ卷
8、17(2)
基本不等式应用
10
Ⅲ卷
13
线性规划求最值
5
年份
卷别
题号
考查角度
分值
2019
Ⅰ卷
1、3、4、8
不等式比较大小推理、框图
20
Ⅱ卷
6
不等式的性质
5
Ⅲ卷
1、9
二次不等式的求解、程序框图
10
2018
Ⅰ卷
2、3、13
集合补集、程序框图、一元二次不等式的解集、线性规划
15
Ⅱ卷
7、14
程序框图、线性规划
10
Ⅲ卷
1、12
一元一次不等式的解集、集合运算、不等式的性质、对数运算
10
(文科)
年份
卷别
题号
考查角度
分值
2020
Ⅰ卷
1、9、13
利用一元二次不等式的解法求集合;程序框图的算法功能;简单线性规划求最值
15
Ⅱ卷
7、15
程序框图的应用;简单线性规划求最值
10
Ⅲ卷
13
简单线性规划求线性目标函数的最大值
5
年份
卷别
题号
考查角度
分值
2019
Ⅰ卷
9
程序框图
5
Ⅱ卷
13
简单线性规划求线性目标函数的最大值
5
Ⅲ卷
9、11
程序框图的应用;简单线性规划的应用
10
2018
Ⅰ卷
14
简单线性规划的应用
5
Ⅱ卷
8、14
程序框图的应用;简单线性规划的应用
10
Ⅲ卷
15
简单线性规划的应用
5
02 考点分类 · 析重点
1.一元二次不等式的解法
先化为一般形式ax2+bx+c>0(a≠0),再求相应一元二次方程ax2+bx+c=0(a≠0)的根,最后根据相应二次函数图象与x轴的位置关系,确定一元二次不等式的解集.
考点一 不等式的性质及解法
D
B
B
4.(2020·重庆朝阳中学期中)关于x的不等式x2-(m+1)x+(m+1)≥0对一切x∈R恒成立,则实数m的取值范围为 ( )
A.[-3,1] B.[-3,3]
C.[-1,1] D.[-1,3]
【解析】 ∵关于x的不等式x2-(m+1)x+(m+1)≥0对一切x∈R恒成立,∴Δ=(m+1)2-4(m+1)=(m+1)(m-3)≤0,
解得-1≤m≤3,∴实数m的取值范围为[-1,3].故选D.
D
不等式的求解技巧
(1)对于和函数有关的不等式,可利用函数的单调性进行转化.
(2)求解一元二次不等式的步骤:
第一步,二次项系数化为正数;
第二步,解相应的一元二次方程;
第三步,若有两个不相等的实根,则利用“大于在两边,小于夹中间”得不等式的解集.
(3)含参数的不等式的求解,要对参数进行分类讨论.
1.线性规划
(1)①不等式y>kx+b表示直线y=kx+b上方区域;
②等式y=kx+b表示直线y=kx+b上的区域;
③不等式y
(2)线性目标函数z=ax+by,作可行域与直线l:ax+by=0,并平移直线l
①b>0时上移l、z增大,下移l、z减小,即“上增下减”;
②b<0时“上减下增”.
D
B
B
B
考向2 基本不等式
5.(2020·吉林省重点中学联考)若实数x,y满足x+y=8,则x2+y2的最小值是 ( )
A.8 B.32
C.16 D.4
B
A
8
8.(2020·江苏省八校联考)已知实数a,b满足4a2-5ab+4b2=9,则a+b最大值为______.
两种循环结构的特点
直到型循环结构:在执行了一次循环体后,对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.
当型循环结构:在每次执行循环体前,对条件进行判断,当条件满足时,执行循环体,否则终止循环.
考点三 算法与程序框图
考向1 直接循环计算
1.(2020·四川省成都七中一诊)执行如图所示的程序框图,输出的S值为 ( )
A.3 B.-6
C.10 D.-15
【解析】 根据程序框图可知S=-12+22-32+42=10,故选C.
C
C
考向2 完善判断框
3.(2020·四川省成都七中模拟)按照如图的程序框图执行,若输出结果为15,则M处条件为 ( )
A.k≥16?
B.k<8?
C.k<16?
D.k≥8?
A
【解析】 根据题中所给的程序框图,可以确定该题要求的是S=1+2+4+8+...,
对应的正好是以1为首项,以2为公比的等比数列,
该数列的前4项和正好是15,结合题中所给的条件,一一试过,可知当k≥16时,退出循环,故选A.
解答程序框图(流程图)问题的方法
(1)首先要读懂程序框图,要熟练掌握程序框图的三种基本结构,特别是循环结构,在累加求和、累乘求积、多次输入等有规律的科学计算中,都有循环结构.
(2)准确把握控制循环的变量,变量的初值和循环条件,弄清在哪一步结束循环;弄清循环体和输入条件、输出结果.
(3)对于循环次数比较少的可逐步写出,对于循环次数较多的可先依次列出前几次循环结果,找出规律.
1.合情推理
合情推理是根据已有的事实和正确的结论推测某些结果的推理过程.通过观察特例,形成猜想,严格论证,是发现(提出)问题,解决问题的常用方法.归纳、类比推理是根据个别事实,通过分析提出猜想的推理,其结论可能是错误的.
考点四 推理与证明
而演绎推理是由一般性原理出发,推出某个特殊情况下的结论,其结论是准确的.在进行类比推理时要尽量从本质上类比,不要被表面现象所迷惑,犯机械类比的错误.类比除了发现结论外,还可以发现证明结论的思路和方法.要善于观察和总结,养成归纳、类比、联想的习惯.
2.反证法
有些问题如果从正面求解繁琐或无法求解时,则可从其反面进行思考,通过否定结论的反面来肯定结论正确,这就是“正难则反”的思路.用反证法证题推出矛盾主要有下列情形:
①与已知条件矛盾;
②与公理、定理、定义及性质矛盾;
③与假设矛盾.
宜用反证法证明的题型:
①易导出与已知矛盾的命题;
②否定性命题;
③唯一性命题;
④至少、至多型命题;
⑤某些基本定理;
⑥必然性命题.
【答案】 C
2.观察下列等式:
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
……
照此规律,第n个等式可为
?
_________________________________________________.
C
考向3 直接证明与间接证明
4.(2020·潍坊检测)用反证法证明命题:“若a∈R,则函数y=x3+ax+b至少有一个零点”时,要做的假设是 ( )
A.函数y=x3+ax+b没有零点
B.函数y=x3+ax+b至多有一个零点
C.函数y=x3+ax+b至多有两个零点
D.函数y=x3+ax+b恰好有一个零点
【解析】 根据反证法的定义,可知“若a∈R,则函数y=x3+ax+b至少有一个零点”的反设应为“若a∈R,则函数y=x3+ax+b没有零点”.故选A.
A
C
1.破解归纳推理题的思维三步骤
(1)发现共性:通过观察特例发现某些相似性(特例的共性或一般规律);
(2)归纳推理:把这种相似性推广为一个明确表述的一般命题(猜想);
(3)检验结论:对所得的一般性命题进行检验,一般地,“求同存异”“逐步细化”“先粗后精”是求解由特殊结论推广到一般结论型创新题的基本技巧.
2.破解类比推理题的三个关键
(1)会定类,即找出两类对象之间可以确切表述的相似特征;
(2)会推测,即用一类事物的性质去推测另一类事物的性质,得出一个明确的猜想;
(3)会检验,即检验猜想的正确性.要将类比推理运用正确.
03 易错清零 · 免失误
(2020·青羊期中)若不等式ax2+2ax-1<0的解集为R,则a的取值范围是___________.
典例1
1.解含参数的不等式时不知道如何对参数分类讨论
(-1,0]
【剖析】 上述解法的错误是忽略了对a的讨论,若在二次不等式中二次项的系数中含有参数,就要讨论二次项系数等于0和不等于0两种情况.
典例2
2.忽略应用基本不等式的前提条件致误
D
(2020·江西名校第一次联考)执行如图所示的程序框图,若输出的S=1 320,则判断框中可填入 ( )
A.k≤12?
B.k≤11?
C.k≤10?
D.k≤9?
典例3
3.错判程序框图中判断框内的条件
D
【解析】 初始值k=12,S=1,
执行框图如下.
S=1,若满足判断框内的条件,则输出1,与已知不符,故判断框内的条件不成立,
S=1×12=12,k=12-1=11;
此时若满足判断框内的条件,则输出12,与已知不符,故判断框内的条件不成立,
S=12×11=132,k=11-1=10;
此时若满足判断框内的条件,则输出132,与已知不符,故判断框内的条件不成立,
S=132×10=1 320,k=10-1=9;
此时若满足判断框内的条件,则输出1 320,与已知相符,故此时判断框内的条件成立.
此时k=9,结合选项可知只有D项满足,故选D.
【剖析】 (1)该题易出现的问题主要是忽视输出结果与判断框内条件的对应,导致判断错误.
(2)解决此类问题需要注意两个方面.一是整体把握程序框图的功能.显然本题中的程序框图的功能是计算12×11×…的值,输出的结果1 320=12×11×10,故当k=10时,仍要进入循环体进行运算,当k=9时,跳出循环体,输出结果,二是要注意判断框内条件的形式.“等号”会影响计算的次数与输出的结果,如该题,若判断框内的条件不带等号,即改为“k<9?”,则需要再进行一次运算,输出的结果就是1 320×9了,事实上,该题中判断框内还可以填入“k<10?”.
(2020·湖南长郡中学模拟)已知从1开始的连续奇数按照蛇形排列形成宝塔形数表,第一行为1,第二行为3,5,第三行为11,9,7,第四行为13,15,17,19,…,如图所示,将在宝塔形数表中位于第i行,第j列的数记为aij,比如a32=9,a42=15,a54=23,若aij=2 019,则i+j= ( )
A.72 B.71
C.66 D.65
典例4
4.归纳不当致误
B
【剖析】 该题易出现的问题主要有以下几个方面:一是不能准确确定2 019在宝塔形数表中的位置,导致判断错误;二是在判断2 019所在行时,不能正确归纳出每行中的奇数的个数,从而导致求得的前i行的奇数个数之和出错,行数定位错误;三是在确定2 019所在列时,不能正确利用其所在行的首位奇数和排列方向,导致列数定位出错,该题根据已如归纳第i行奇数的个数以及第i行奇数的排列顺序是关键.
04 真题回放 · 悟高考
C
A
B
【解析】 把各循环变量在各次循环中的值用表格表示如下.
4.(2019·全国Ⅱ理6)若a>b,则 ( )
A.ln (a-b)>0 B.3a<3b
C.a3-b3>0 D.|a|>|b|
C
5.(2019·全国卷Ⅱ)在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测.
甲:我的成绩比乙高.
乙:丙的成绩比我和甲的都高.
丙:我的成绩比乙高.
成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为 ( )
A.甲、乙、丙 B.乙、甲、丙
C.丙、乙、甲 D.甲、丙、乙
A
【解析】 若甲预测正确,则乙、丙预测错误,则甲比乙成绩高,丙比乙成绩低,故3人成绩由高到低依次为甲,乙,丙;若乙预测正确,则丙预测也正确,不符合题意;若丙预测正确,则甲必预测错误,丙比乙的成绩高,乙比甲成绩高,即丙比甲,乙成绩都高,即乙预测正确,不符合题意.故选A.
6.(2020·全国卷Ⅰ卷)执行下面的程序框图,则输出的n= ( )
A.17
B.19
C.21
D.23
C
7.(2020·全国卷Ⅱ卷)执行下面的程序框图,若输入的k=0,a=0,则输出的k为 ( )
A.2
B.3
C.4
D.5
C
【解析】 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出的k值
模拟程序的运行过程
k=0,a=0
第1次循环,a=2×0+1=1,k=0+1=1,1>10为否
第2次循环,a=2×1+1=3,k=1+1=2,3>10为否
第3次循环,a=2×3+1=7,k=2+1=3,7>10为否
第4次循环,a=2×7+1=15,k=3+1=4,15>10为是
退出循环
输出k=4.
故选C.
1
【解析】 绘制不等式组表示的平面区域如图所示,
7
【解析】 不等式组所表示的可行域如图:
同课章节目录
