3.7弧长及扇形的面积课件
图片预览



文档简介
(共16张PPT)
3.7弧长及扇形的面积
九年级数学(上)第三章圆
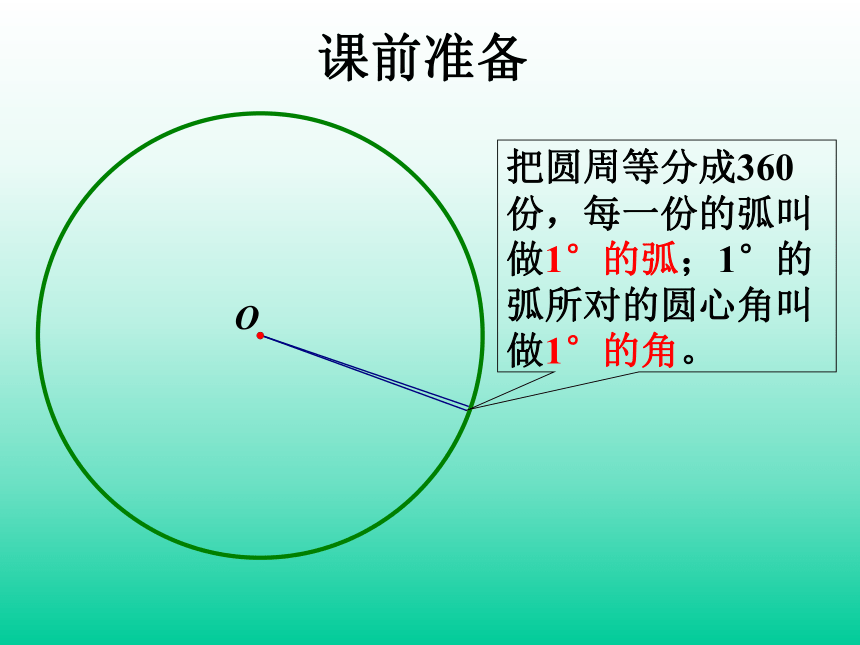
把圆周等分成360份,每一份的弧叫做1°的弧;1°的弧所对的圆心角叫做1°的角。
课前准备
探索弧长公式
设一圆的圆心为O,半径为r。
圆周长为多少
圆周角为360°,则1°的圆心角所对的弧长为多少?
n°的圆心角所对的弧长为多少
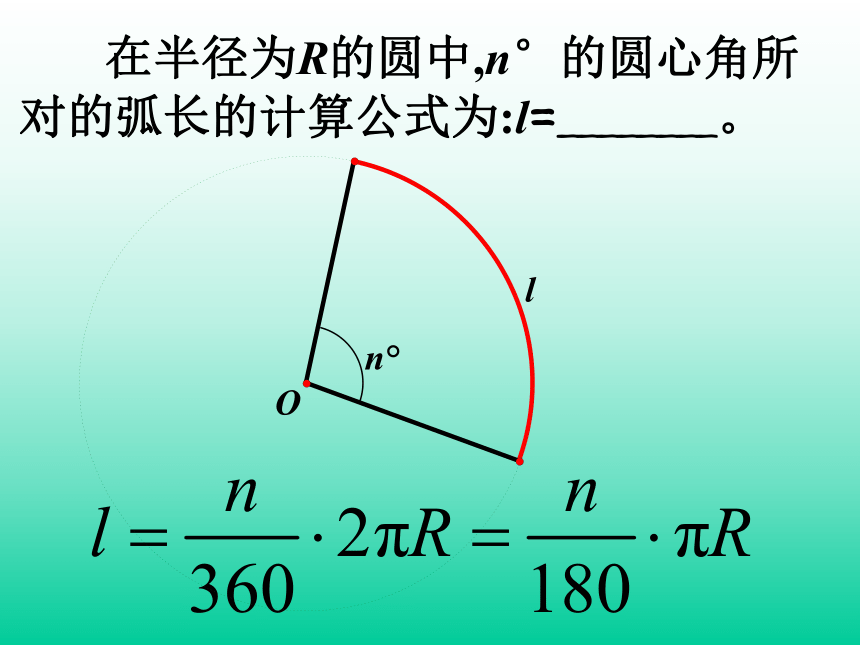
在半径为R的圆中,n°的圆心角所对的弧长的计算公式为:l=________。
探索弧长公式
设一圆的为⊙O,半径为r。
圆面积为多少
圆周角为360°,则1°的圆心角所对的扇形面积为多少?
n°的圆心角所对的扇形面积为多少
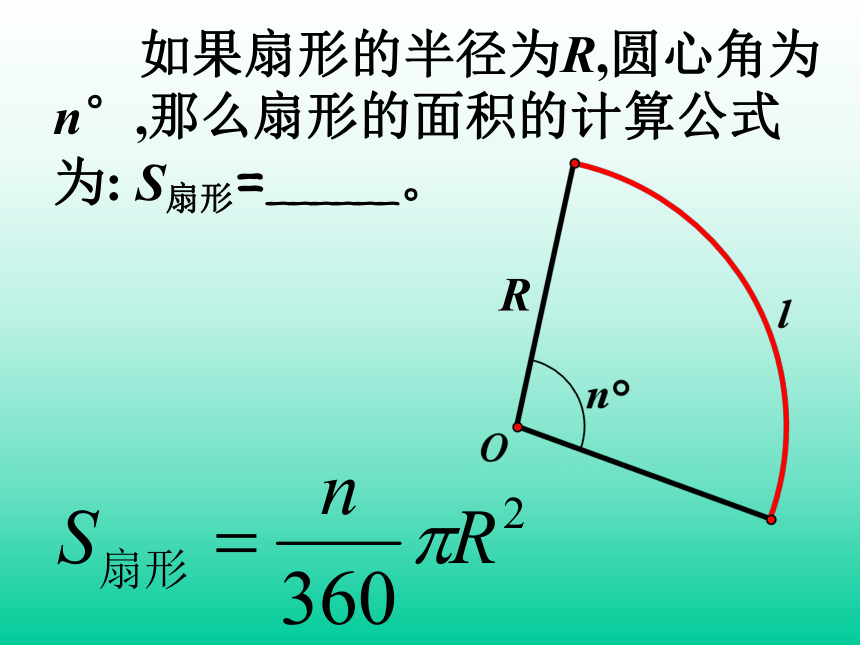
如果扇形的半径为R,圆心角为n°,那么扇形的面积的计算公式为: S扇形=______。
R
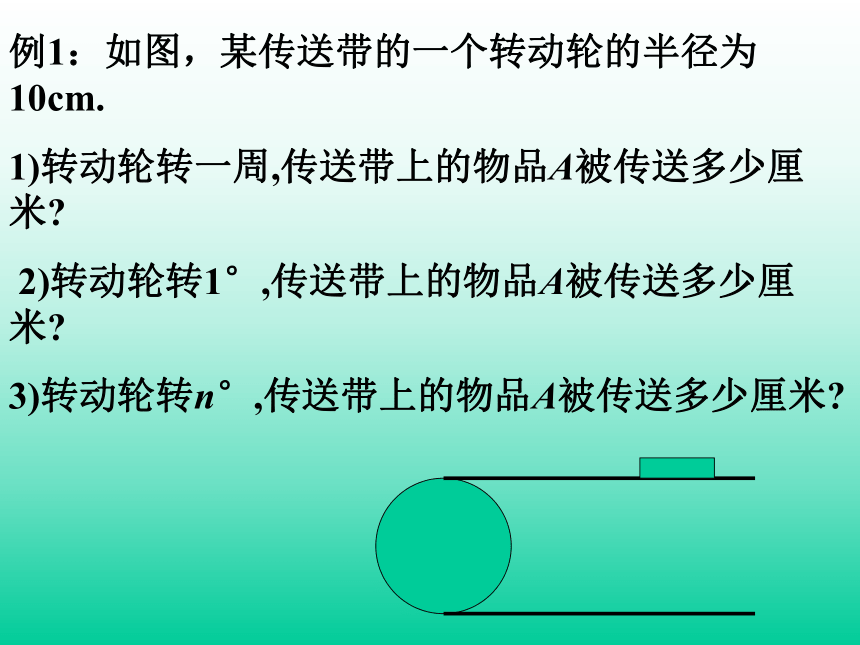
例1:如图,某传送带的一个转动轮的半径为10cm.
1)转动轮转一周,传送带上的物品A被传送多少厘米
2)转动轮转1°,传送带上的物品A被传送多少厘米
3)转动轮转n°,传送带上的物品A被传送多少厘米
例2:制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算如图所示的管道的展直长度,即弧AB的长.
解:R=40mm, n=110,
∴弧AB的长
例3:在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗. 1)这只狗的最大活动区域有多大
2)如果这只够只能绕柱子转过n°角,那么它的最大活动区域有多大
n°
l
O
比较扇形面积(S)公式和弧长(l)公式,你能用弧长来表示扇形的面积吗
探索弧长与扇形面积的关系
S
R
例4:扇形AOB的半径12cm,∠AOB=120°,
求弧AB的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到0.1cm2)
练习1:如图,已知扇形的圆心角为150°,弧长为20πcm,求扇形的半径.
O
A
B
练习2:如图,圆心角为60°的扇形的半径为10cm, 求这个扇形的面积和周长.
O
A
B
练习3:扇形的面积是S,它的半径是r,求这个扇形的弧长.
练习4:如图,在同心圆中,两圆半径分别为2, 1,∠AOB=120°,求阴影部分的面积.
A
B
O
120°
B
C
A
练习5:⊙A, ⊙B, ⊙C两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少 弧长的和为多少
B
C
A
D
练习6:⊙A, ⊙B, ⊙C, ⊙D两两不相交,且半径都是1cm,则图中的四个扇形的面积之和为多少 弧长的和为多少
B
C
A
D
练习7:⊙A, ⊙B, ⊙C, ⊙D ,⊙E两两不相交,且半径都是1cm,则图中的五个扇形的面积之和为多少 弧长的和为多少
E
若象这样的n个圆呢?
3.7弧长及扇形的面积
九年级数学(上)第三章圆
把圆周等分成360份,每一份的弧叫做1°的弧;1°的弧所对的圆心角叫做1°的角。
课前准备
探索弧长公式
设一圆的圆心为O,半径为r。
圆周长为多少
圆周角为360°,则1°的圆心角所对的弧长为多少?
n°的圆心角所对的弧长为多少
在半径为R的圆中,n°的圆心角所对的弧长的计算公式为:l=________。
探索弧长公式
设一圆的为⊙O,半径为r。
圆面积为多少
圆周角为360°,则1°的圆心角所对的扇形面积为多少?
n°的圆心角所对的扇形面积为多少
如果扇形的半径为R,圆心角为n°,那么扇形的面积的计算公式为: S扇形=______。
R
例1:如图,某传送带的一个转动轮的半径为10cm.
1)转动轮转一周,传送带上的物品A被传送多少厘米
2)转动轮转1°,传送带上的物品A被传送多少厘米
3)转动轮转n°,传送带上的物品A被传送多少厘米
例2:制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算如图所示的管道的展直长度,即弧AB的长.
解:R=40mm, n=110,
∴弧AB的长
例3:在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗. 1)这只狗的最大活动区域有多大
2)如果这只够只能绕柱子转过n°角,那么它的最大活动区域有多大
n°
l
O
比较扇形面积(S)公式和弧长(l)公式,你能用弧长来表示扇形的面积吗
探索弧长与扇形面积的关系
S
R
例4:扇形AOB的半径12cm,∠AOB=120°,
求弧AB的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到0.1cm2)
练习1:如图,已知扇形的圆心角为150°,弧长为20πcm,求扇形的半径.
O
A
B
练习2:如图,圆心角为60°的扇形的半径为10cm, 求这个扇形的面积和周长.
O
A
B
练习3:扇形的面积是S,它的半径是r,求这个扇形的弧长.
练习4:如图,在同心圆中,两圆半径分别为2, 1,∠AOB=120°,求阴影部分的面积.
A
B
O
120°
B
C
A
练习5:⊙A, ⊙B, ⊙C两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少 弧长的和为多少
B
C
A
D
练习6:⊙A, ⊙B, ⊙C, ⊙D两两不相交,且半径都是1cm,则图中的四个扇形的面积之和为多少 弧长的和为多少
B
C
A
D
练习7:⊙A, ⊙B, ⊙C, ⊙D ,⊙E两两不相交,且半径都是1cm,则图中的五个扇形的面积之和为多少 弧长的和为多少
E
若象这样的n个圆呢?
