2.5.2 二次函数与一元二次方程 课件(共27张PPT)
文档属性
| 名称 | 2.5.2 二次函数与一元二次方程 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 18:08:15 | ||
图片预览






文档简介
第5节 二次函数与一元二次方程
(第2课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.会用二次函数图象求一元二次方程的近似解及一元二次不等式的解集; (重点)
2.通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.(难点)
学习目标
二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?
二次函数y=ax2+bx+c的图象和x轴交点
一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
两个相异的实根
b2-4ac > 0
有一个交点
两个相等的实根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
新课导入
用图象法求一元二次方程的近似解
知识点一
你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗?
探究新知
如图是函数y=x2+2x-10的图象.由图象可知方程有两个根,一个在-5和-4之间,另一个在2和3之间.
(1)先求-5和-4之间的根.利用计算器进行探索:
{073A0DAA-6AF3-43AB-8588-CEC1D06C72B9}x
-4.1
-4.2
-4.3
-4.4
y
-1.39
-0.76
-0.11
0.56
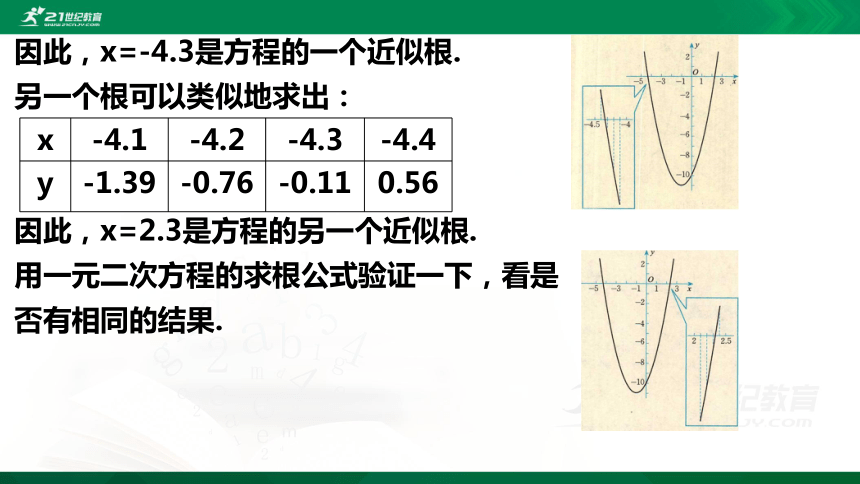
因此,x=-4.3是方程的一个近似根.
另一个根可以类似地求出:
因此,x=2.3是方程的另一个近似根.
用一元二次方程的求根公式验证一下,看是否有相同的结果.
{073A0DAA-6AF3-43AB-8588-CEC1D06C72B9}x
-4.1
-4.2
-4.3
-4.4
y
-1.39
-0.76
-0.11
0.56
总结:利用二次函数的图象求一元二次方程的近似根的一般步骤:
(1)画出二次函数y=ax2+bx+c的图象;
(2)确定二次函数的图象与x轴交点的个数,看交点的横坐标在哪两个整数之间;
(3)列表,在两个整数之间取值,并用计算器算出对应的y值,当x由x1变到x2,对应的y值出现y1>0,y2<0(或y1<0,y2>0)且|y1|≠|y2|时,x1,x2中必有一个是方程的近似根,再比较|y1|和|y2|,若|y1|<|y2|,则x1是方程的近似根;若|y1|>|y2|,则x2是方程的近似根.
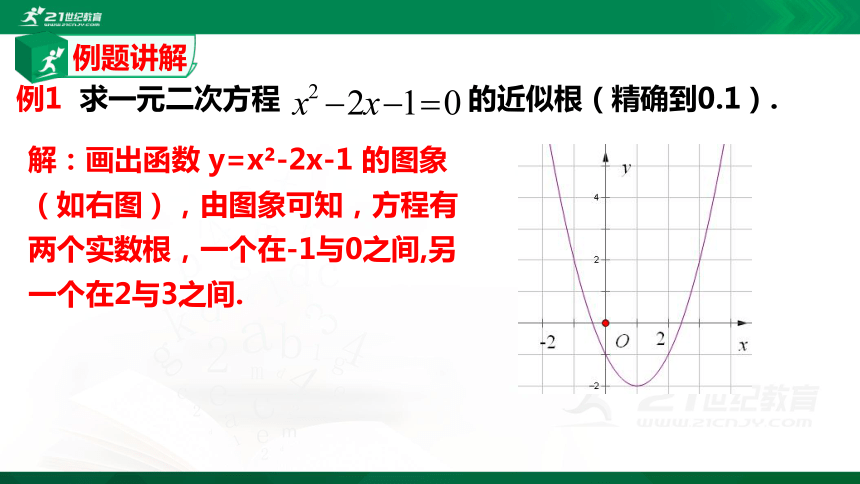
例1 求一元二次方程 的近似根(精确到0.1).
解:画出函数 y=x?-2x-1 的图象(如右图),由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.
例题讲解
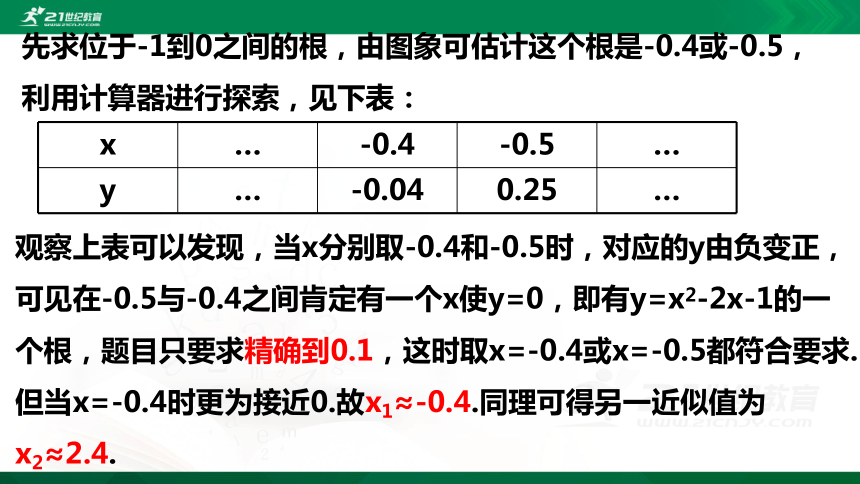
先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:
x
…
-0.4
-0.5
…
y
…
-0.04
0.25
…
观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.同理可得另一近似值为x2≈2.4.
(1)用描点法作二次函数 y=ax2+bx+c的图象;
(2)观察估计二次函数 的图象与x轴的交点的横坐标;
(可将单位长度十等分,借助计算器确定其近似值);
(3)确定方程ax2+bx+c=0的近似根;
总结:利用图象法求一元二次方程的近似根
解:先把方程化成x2=-2x+3.如图,
在同一直角坐标系中分别画出函数
y=x2和y=-2x+3的图象,得到它
则方程x2+2x-3=0的解为x=-3或x=1.
例2 利用函数的图象,求方程x2+2x-3=0的根.
例题讲解
总结:利用图象交点法求一元二次方程的根的步骤:
(1)将ax2+bx+c=0化为ax2=-bx-c的形式;
(2)在同一坐标系中画出y=ax2与y=-bx-c的图象;
(3)观察图象:两图象的公共点情况即为方程的根的情况,如有公共点,则公共点的横坐标即为ax2+bx+c=0的根.
用图象法求一元二次不等式的解集
知识点二
问题1 函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=0的根是 _____ _____;
不等式ax2+bx+c>0的解集是___________;
不等式ax2+bx+c<0的解集是_________.
3
-1
O
x
y
x1=-1, x2=3
x<-1或x>3
-1问题2 函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=2的根是 ______________;
不等式ax2+bx+c>2的解集是___________;
不等式ax2+bx+c<2的解集是_________.
3
-1
O
x
2
(4,2)
(-2,2)
x1=-2, x2=4
x<-2或x>4
-2y
问题3 如果不等式ax2+bx+c>0(a≠0)的解集是x≠2 的一切实数,那么函数y=ax2+bx+c的图象与 x轴有____ 个交点,坐标是______.方程ax2+bx+c=0的根是______.
1
(2,0)
x=2
问题4 如果方程ax2+bx+c=0 (a≠0)没有实数根,那么函数y=ax2+bx+c的图象与 x轴有______个交点;不等式ax2+bx+c<0的解集是多少?
0
解:(1)当a>0时, ax2+bx+c<0无解;
(2)当a<0时, ax2+bx+c<0的解集是一切实数.
例3 画出抛物线y=-x2+4x+5,观察抛物线,回答下列问题:
(1)x为何值时,函数值y>0?
(2)x为何值时,函数值y=0?
(3)x为何值时,函数值y<0?
例题讲解
解:∵y=-x2+4x+5=-(x2-4x)+5=-(x2-4x+4)+9=-(x-2)2+9.∴抛物线的顶点坐标为(2,9),对称轴为直线x=2.
令-x2+4x+5=0,即x2-4x-5=0,∴x1=5,x2=-1.
∴抛物线与x轴的两个交点为(-1,0),(5,0).
令x=0,则y=5,即抛物线与y轴的交点为(0,5).由抛物线的对称性知抛物线上的另一点为(4,5).在坐标系中描出各点,并连线得到如图所示的图象.观察图象会发现:
(1)当-1<x<5时,函数值y>0;
(2)当x=-1或x=5时,函数值y=0;
(3)当x<-1或x>5时,函数值y<0
二次函y=ax2+bx+c的图象与x轴交点
a>0
a<0
有两个交点x1,x2 (x1<x2)
有一个交点x0
没有交点
y<0,x1<x<x2.
y>0,x2<x或x<x1
y>0,x1<x<x2.
y<0,x2<x或x<x1
y>0,x0之外的所有实数;y<0,无解
y<0,x0之外的所有实数;y>0,无解
y>0,所有实数;
y<0,无解
y<0,所有实数;
y>0,无解
总结:二次函数y=ax2+bx+c的图象与x轴交点的坐标与
一元二次不等式的关系
例4 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点A在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:①4ac-b2<0;②2a-b=0;③a+b+c<0; ④点M(x1,y1),N(x2,y2)在抛物线上,若x1<x2,则y1<y2.正确结论的个数是( )
A.1 B.2
C.3 D.4
C
例题讲解
1 已知一次函数y1=4x,二次函数y2=2x2+2,在实数范围内,对于x的同一个值,这两个函数所对应的函数值分别为y1与y2,则下列关系正确的是( )
A.y1>y2 B.y1≥y2
C.y1<y2 D.y1≤y2
课堂练习
2 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
A.b2>4ac
B.ax2+bx+c≥-6
C.若点(-2,m),(-5,n)
在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=-4
的两根为-5和-1
3 已知二次函数 的图象,利用图象回答问题:
(1)方程 的解是什么?
(2)x取什么值时,y>0 ?
(3)x取什么值时,y<0 ?
x
y
O
2
4
8
利用图象求一元二次方程的根的方法:直接画出二次函数y=ax2+bx+c的图象,则图象与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.其步骤一般为
(1)作出二次函数y=ax2+bx+c的图象;
(2)观察图象与x轴交点的个数;
(3)若图象与x轴有交点,估计出图象与x轴交点的横坐标即可得到一元二次方程的近似根.
课堂小结
图象
函数值
自变量的取值(范围)
y>0
x<x1或x>x2
y=0
x=x1或x=x2
y<0
x1<x<x2
y>0
x1<x<x2
y=0
x=x1或x=x2
y<0
x<x1或x>x2
谢谢聆听
(第2课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.会用二次函数图象求一元二次方程的近似解及一元二次不等式的解集; (重点)
2.通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.(难点)
学习目标
二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?
二次函数y=ax2+bx+c的图象和x轴交点
一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
两个相异的实根
b2-4ac > 0
有一个交点
两个相等的实根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
新课导入
用图象法求一元二次方程的近似解
知识点一
你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗?
探究新知
如图是函数y=x2+2x-10的图象.由图象可知方程有两个根,一个在-5和-4之间,另一个在2和3之间.
(1)先求-5和-4之间的根.利用计算器进行探索:
{073A0DAA-6AF3-43AB-8588-CEC1D06C72B9}x
-4.1
-4.2
-4.3
-4.4
y
-1.39
-0.76
-0.11
0.56
因此,x=-4.3是方程的一个近似根.
另一个根可以类似地求出:
因此,x=2.3是方程的另一个近似根.
用一元二次方程的求根公式验证一下,看是否有相同的结果.
{073A0DAA-6AF3-43AB-8588-CEC1D06C72B9}x
-4.1
-4.2
-4.3
-4.4
y
-1.39
-0.76
-0.11
0.56
总结:利用二次函数的图象求一元二次方程的近似根的一般步骤:
(1)画出二次函数y=ax2+bx+c的图象;
(2)确定二次函数的图象与x轴交点的个数,看交点的横坐标在哪两个整数之间;
(3)列表,在两个整数之间取值,并用计算器算出对应的y值,当x由x1变到x2,对应的y值出现y1>0,y2<0(或y1<0,y2>0)且|y1|≠|y2|时,x1,x2中必有一个是方程的近似根,再比较|y1|和|y2|,若|y1|<|y2|,则x1是方程的近似根;若|y1|>|y2|,则x2是方程的近似根.
例1 求一元二次方程 的近似根(精确到0.1).
解:画出函数 y=x?-2x-1 的图象(如右图),由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.
例题讲解
先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:
x
…
-0.4
-0.5
…
y
…
-0.04
0.25
…
观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.同理可得另一近似值为x2≈2.4.
(1)用描点法作二次函数 y=ax2+bx+c的图象;
(2)观察估计二次函数 的图象与x轴的交点的横坐标;
(可将单位长度十等分,借助计算器确定其近似值);
(3)确定方程ax2+bx+c=0的近似根;
总结:利用图象法求一元二次方程的近似根
解:先把方程化成x2=-2x+3.如图,
在同一直角坐标系中分别画出函数
y=x2和y=-2x+3的图象,得到它
则方程x2+2x-3=0的解为x=-3或x=1.
例2 利用函数的图象,求方程x2+2x-3=0的根.
例题讲解
总结:利用图象交点法求一元二次方程的根的步骤:
(1)将ax2+bx+c=0化为ax2=-bx-c的形式;
(2)在同一坐标系中画出y=ax2与y=-bx-c的图象;
(3)观察图象:两图象的公共点情况即为方程的根的情况,如有公共点,则公共点的横坐标即为ax2+bx+c=0的根.
用图象法求一元二次不等式的解集
知识点二
问题1 函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=0的根是 _____ _____;
不等式ax2+bx+c>0的解集是___________;
不等式ax2+bx+c<0的解集是_________.
3
-1
O
x
y
x1=-1, x2=3
x<-1或x>3
-1
方程ax2+bx+c=2的根是 ______________;
不等式ax2+bx+c>2的解集是___________;
不等式ax2+bx+c<2的解集是_________.
3
-1
O
x
2
(4,2)
(-2,2)
x1=-2, x2=4
x<-2或x>4
-2
问题3 如果不等式ax2+bx+c>0(a≠0)的解集是x≠2 的一切实数,那么函数y=ax2+bx+c的图象与 x轴有____ 个交点,坐标是______.方程ax2+bx+c=0的根是______.
1
(2,0)
x=2
问题4 如果方程ax2+bx+c=0 (a≠0)没有实数根,那么函数y=ax2+bx+c的图象与 x轴有______个交点;不等式ax2+bx+c<0的解集是多少?
0
解:(1)当a>0时, ax2+bx+c<0无解;
(2)当a<0时, ax2+bx+c<0的解集是一切实数.
例3 画出抛物线y=-x2+4x+5,观察抛物线,回答下列问题:
(1)x为何值时,函数值y>0?
(2)x为何值时,函数值y=0?
(3)x为何值时,函数值y<0?
例题讲解
解:∵y=-x2+4x+5=-(x2-4x)+5=-(x2-4x+4)+9=-(x-2)2+9.∴抛物线的顶点坐标为(2,9),对称轴为直线x=2.
令-x2+4x+5=0,即x2-4x-5=0,∴x1=5,x2=-1.
∴抛物线与x轴的两个交点为(-1,0),(5,0).
令x=0,则y=5,即抛物线与y轴的交点为(0,5).由抛物线的对称性知抛物线上的另一点为(4,5).在坐标系中描出各点,并连线得到如图所示的图象.观察图象会发现:
(1)当-1<x<5时,函数值y>0;
(2)当x=-1或x=5时,函数值y=0;
(3)当x<-1或x>5时,函数值y<0
二次函y=ax2+bx+c的图象与x轴交点
a>0
a<0
有两个交点x1,x2 (x1<x2)
有一个交点x0
没有交点
y<0,x1<x<x2.
y>0,x2<x或x<x1
y>0,x1<x<x2.
y<0,x2<x或x<x1
y>0,x0之外的所有实数;y<0,无解
y<0,x0之外的所有实数;y>0,无解
y>0,所有实数;
y<0,无解
y<0,所有实数;
y>0,无解
总结:二次函数y=ax2+bx+c的图象与x轴交点的坐标与
一元二次不等式的关系
例4 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点A在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:①4ac-b2<0;②2a-b=0;③a+b+c<0; ④点M(x1,y1),N(x2,y2)在抛物线上,若x1<x2,则y1<y2.正确结论的个数是( )
A.1 B.2
C.3 D.4
C
例题讲解
1 已知一次函数y1=4x,二次函数y2=2x2+2,在实数范围内,对于x的同一个值,这两个函数所对应的函数值分别为y1与y2,则下列关系正确的是( )
A.y1>y2 B.y1≥y2
C.y1<y2 D.y1≤y2
课堂练习
2 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
A.b2>4ac
B.ax2+bx+c≥-6
C.若点(-2,m),(-5,n)
在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=-4
的两根为-5和-1
3 已知二次函数 的图象,利用图象回答问题:
(1)方程 的解是什么?
(2)x取什么值时,y>0 ?
(3)x取什么值时,y<0 ?
x
y
O
2
4
8
利用图象求一元二次方程的根的方法:直接画出二次函数y=ax2+bx+c的图象,则图象与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.其步骤一般为
(1)作出二次函数y=ax2+bx+c的图象;
(2)观察图象与x轴交点的个数;
(3)若图象与x轴有交点,估计出图象与x轴交点的横坐标即可得到一元二次方程的近似根.
课堂小结
图象
函数值
自变量的取值(范围)
y>0
x<x1或x>x2
y=0
x=x1或x=x2
y<0
x1<x<x2
y>0
x1<x<x2
y=0
x=x1或x=x2
y<0
x<x1或x>x2
谢谢聆听
