2.2.4二次函数的图像与性质 课件(共23张PPT)
文档属性
| 名称 | 2.2.4二次函数的图像与性质 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 22:20:49 | ||
图片预览






文档简介
第2节 二次函数的图像与性质
(第4课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.体会建立二次函数对称轴和顶点坐标公式的必要性.
2.能够作出y=a(x-h)2和y=a(x-h)2+k的图象,并能理解它与y=ax2的图象的关系.理解a,h和k对二次函数图象的影响.
3.能够正确说出y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标.
学习目标
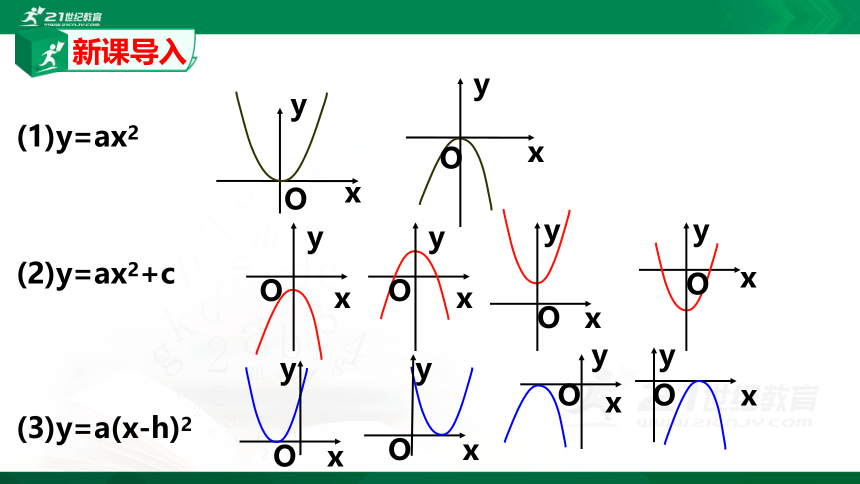
(1)y=ax2
(2)y=ax2+c
(3)y=a(x-h)2
y
y
y
y
x
x
x
x
O
O
O
O
y
y
y
y
x
x
x
x
O
O
O
O
y
y
x
x
O
O
新课导入
二次函数y=a(x-h)2+k的图象
知识点一
1.画出函数 的图象.指出它的开口方向、顶点、对称轴与增减性.
探究新知
…
…
…
…
2
1
0
-1
-2
-3
-4
x
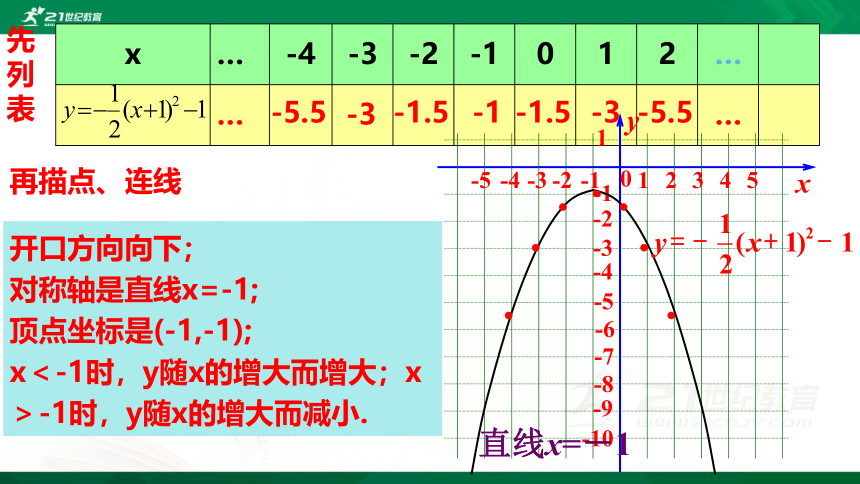
先列表
再描点、连线
-5.5
-3
-1.5
-1
-1.5
-3
-5.5
开口方向向下;
对称轴是直线x=-1;
顶点坐标是(-1,-1);
x<-1时,y随x的增大而增大;x>-1时,y随x的增大而减小.
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
0
-1
-2
-3
-4
-5
-10
直线x=-1
例1 对于抛物线y=-(x+1)2+3,下列结论:
① 抛物线的开口向下;② 对称轴为直线x=1;③ 顶点坐标为(-1,3);④ x>1 时,y 随x 的增大而减小.
其中正确结论有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
C
例题讲解
总结:解答抛物线y=a(x-h)2+k 的开口方向、对称轴、顶点坐标、最值、增减性规律等问题,首先必须弄清顶点式y=a(x-h)2+k中a,h,k 与开口方向、对称轴、顶点坐标、最值间的关系,比较题中给出的相关数据与a,h,k 间的关系,再结合相关知识按题目要求解答.
二次函数y=a(x-h)2+k的性质
知识点二
议一议
观察图象得到:抛物线的开口向下,
对称轴是直线x=-1,
顶点是(-1, -1).
抛物线 的开口方向、对称轴、顶点?
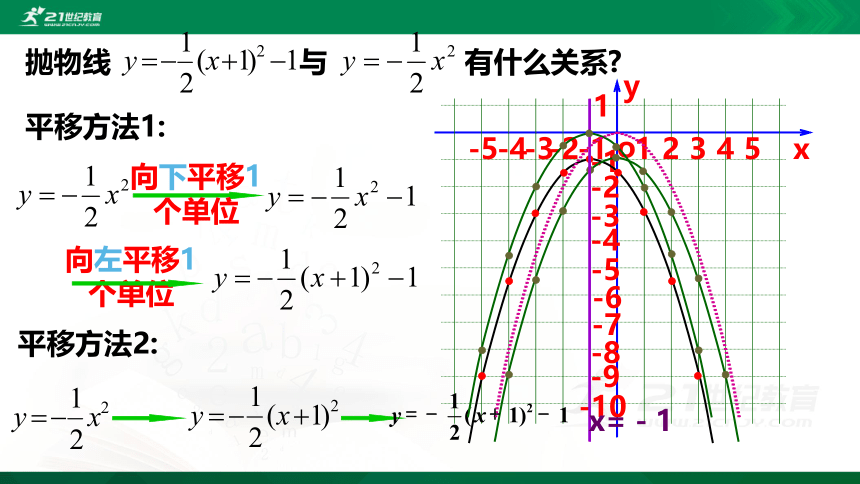
向左平移1个单位
向下平移1个单位
平移方法1:
平移方法2:
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x=-1
抛物线 与 有什么关系?
二次函数 y=a(x-h)2+k的性质
y=a(x-h)2+k
a>0
a<0
开口方向
对称轴
顶点坐标
最值
增减性
要点归纳
向上
向下
直线x=h
直线x=h
(h,k)
(h,k)
当x=h时,y最小值=k
当x=h时,y最大值=k
当x<h时,y随x的增大而减小;
x>h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;
x<h时,y随x的增大而增大.
例2 已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
解析:根据二次函数开口向上则a>0,根据-c是二次函数顶点坐标的纵坐标,得出c>0,故一次函数y=ax+c的大致图象经过第一、二、三象限.故选A.
A
例题讲解
例3 若二次函数y=(x-m)2-1,当x≤1时,y随x的增大而减小,则m的取值范围是( )
A.m=1 B.m>1
C.m≥1 D.m≤1
C
例题讲解
二次函数y=a(x-h)2+k与y=ax2图象间的平移关系
知识点三
向左平移
1个单位
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
怎样移动抛物线 就可以得到抛物线 ?
平移方法1
向下平移
1个单位
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
怎样移动抛物线 就可以得到抛物线 ?
平移方法2
向左平移
1个单位
向下平移
1个单位
要点归纳
二次函数y=ax2 与y=a(x-h)2+k的关系
可以看作互相平移得到的(h>0,k>0).
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下
平移
左右
平移
上下
平移
左右
平移
平移规律
简记为:
上下平移,
括号外上加下减;
左右平移,
括号内左加右减.
二次项系数a不变.
例4 将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线对应的函数关系式为( )
A.y=3(x+2)2+3 B.y=3(x-2)2+3
C.y=3(x+2)2-3 D.y=3(x-2)2-3
A
总结:将抛物线在平面直角坐标系中平移,关键就是顶点坐标在发生变化,抛物线的形状和大小不变,故紧扣顶点式y=a(x-h)2+k中h,k的变化即可.
例题讲解
1.抛物线y=2(x-3)2+4的顶点坐标是( )
A.(3,4) B.(-3,4)
C.(3,-4) D.(2,4)
课堂练习
2.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( )
A.m>1 B.m>0
C.m>-1 D.-1<m<0
3.将抛物线y=2(x-4)2-1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线对应的函数表达式为( )
A.y=2x2+1 B.y=2x2-3
C.y=2(x-8)2+1 D.y=2(x-8)2-3
4.如图,在△ABC中,∠C=90°,AB=10 cm,BC=8 cm,点P从点A沿AC向点C以1 cm/s的速度运动,同时点Q从点C沿CB向点B以2 cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19 cm2 B.16 cm2
C.15 cm2 D.12 cm2
5.将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式是( )
A.y=(x+2)2+1
B.y=(x+2)2-1
C.y=(x-2)2+1
D.y=(x-2)2-1
一般地,抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同.
二次函数y=a(x-h)2+k的图象和性质
图象特点
当a>0,开口向上;当a<0,开口向下.
对称轴是x=h,
顶点坐标是(h,k).
平移规律
左右平移:括号内左加右减;
上下平移:括号外上加下减.
课堂小结
谢谢聆听
(第4课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.体会建立二次函数对称轴和顶点坐标公式的必要性.
2.能够作出y=a(x-h)2和y=a(x-h)2+k的图象,并能理解它与y=ax2的图象的关系.理解a,h和k对二次函数图象的影响.
3.能够正确说出y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标.
学习目标
(1)y=ax2
(2)y=ax2+c
(3)y=a(x-h)2
y
y
y
y
x
x
x
x
O
O
O
O
y
y
y
y
x
x
x
x
O
O
O
O
y
y
x
x
O
O
新课导入
二次函数y=a(x-h)2+k的图象
知识点一
1.画出函数 的图象.指出它的开口方向、顶点、对称轴与增减性.
探究新知
…
…
…
…
2
1
0
-1
-2
-3
-4
x
先列表
再描点、连线
-5.5
-3
-1.5
-1
-1.5
-3
-5.5
开口方向向下;
对称轴是直线x=-1;
顶点坐标是(-1,-1);
x<-1时,y随x的增大而增大;x>-1时,y随x的增大而减小.
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
0
-1
-2
-3
-4
-5
-10
直线x=-1
例1 对于抛物线y=-(x+1)2+3,下列结论:
① 抛物线的开口向下;② 对称轴为直线x=1;③ 顶点坐标为(-1,3);④ x>1 时,y 随x 的增大而减小.
其中正确结论有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
C
例题讲解
总结:解答抛物线y=a(x-h)2+k 的开口方向、对称轴、顶点坐标、最值、增减性规律等问题,首先必须弄清顶点式y=a(x-h)2+k中a,h,k 与开口方向、对称轴、顶点坐标、最值间的关系,比较题中给出的相关数据与a,h,k 间的关系,再结合相关知识按题目要求解答.
二次函数y=a(x-h)2+k的性质
知识点二
议一议
观察图象得到:抛物线的开口向下,
对称轴是直线x=-1,
顶点是(-1, -1).
抛物线 的开口方向、对称轴、顶点?
向左平移1个单位
向下平移1个单位
平移方法1:
平移方法2:
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x=-1
抛物线 与 有什么关系?
二次函数 y=a(x-h)2+k的性质
y=a(x-h)2+k
a>0
a<0
开口方向
对称轴
顶点坐标
最值
增减性
要点归纳
向上
向下
直线x=h
直线x=h
(h,k)
(h,k)
当x=h时,y最小值=k
当x=h时,y最大值=k
当x<h时,y随x的增大而减小;
x>h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;
x<h时,y随x的增大而增大.
例2 已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
解析:根据二次函数开口向上则a>0,根据-c是二次函数顶点坐标的纵坐标,得出c>0,故一次函数y=ax+c的大致图象经过第一、二、三象限.故选A.
A
例题讲解
例3 若二次函数y=(x-m)2-1,当x≤1时,y随x的增大而减小,则m的取值范围是( )
A.m=1 B.m>1
C.m≥1 D.m≤1
C
例题讲解
二次函数y=a(x-h)2+k与y=ax2图象间的平移关系
知识点三
向左平移
1个单位
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
怎样移动抛物线 就可以得到抛物线 ?
平移方法1
向下平移
1个单位
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
O
-1
-2
-3
-4
-5
-10
怎样移动抛物线 就可以得到抛物线 ?
平移方法2
向左平移
1个单位
向下平移
1个单位
要点归纳
二次函数y=ax2 与y=a(x-h)2+k的关系
可以看作互相平移得到的(h>0,k>0).
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下
平移
左右
平移
上下
平移
左右
平移
平移规律
简记为:
上下平移,
括号外上加下减;
左右平移,
括号内左加右减.
二次项系数a不变.
例4 将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线对应的函数关系式为( )
A.y=3(x+2)2+3 B.y=3(x-2)2+3
C.y=3(x+2)2-3 D.y=3(x-2)2-3
A
总结:将抛物线在平面直角坐标系中平移,关键就是顶点坐标在发生变化,抛物线的形状和大小不变,故紧扣顶点式y=a(x-h)2+k中h,k的变化即可.
例题讲解
1.抛物线y=2(x-3)2+4的顶点坐标是( )
A.(3,4) B.(-3,4)
C.(3,-4) D.(2,4)
课堂练习
2.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( )
A.m>1 B.m>0
C.m>-1 D.-1<m<0
3.将抛物线y=2(x-4)2-1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线对应的函数表达式为( )
A.y=2x2+1 B.y=2x2-3
C.y=2(x-8)2+1 D.y=2(x-8)2-3
4.如图,在△ABC中,∠C=90°,AB=10 cm,BC=8 cm,点P从点A沿AC向点C以1 cm/s的速度运动,同时点Q从点C沿CB向点B以2 cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19 cm2 B.16 cm2
C.15 cm2 D.12 cm2
5.将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式是( )
A.y=(x+2)2+1
B.y=(x+2)2-1
C.y=(x-2)2+1
D.y=(x-2)2-1
一般地,抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同.
二次函数y=a(x-h)2+k的图象和性质
图象特点
当a>0,开口向上;当a<0,开口向下.
对称轴是x=h,
顶点坐标是(h,k).
平移规律
左右平移:括号内左加右减;
上下平移:括号外上加下减.
课堂小结
谢谢聆听
