2.2.5二次函数的图像与性质 课件(共29张PPT)
文档属性
| 名称 | 2.2.5二次函数的图像与性质 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 22:23:14 | ||
图片预览








文档简介
第2节 二次函数的图像与性质
(第5课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
2.能够利用二次函数的对称轴和顶点坐标公式解决一些数学问题.
1.经历探索y=ax2+bx+c的图象特征,会用配方法求其对称轴、顶点坐标公式.
学习目标
二次函数y=a(x-h)2+k的性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
(h,k)
(h,k)
直线x=h
向上
向下
当x=h时,y有最小值为k.
当x=h时, y有最大值为k.
当xh时, y随着x的增大而增大.
根据图象填表:
直线x=h
当xh时, y随着x的增大而减小.
y=a(x-h)2+k(a<0)
y=a(x-h)2+k(a>0)
新课导入
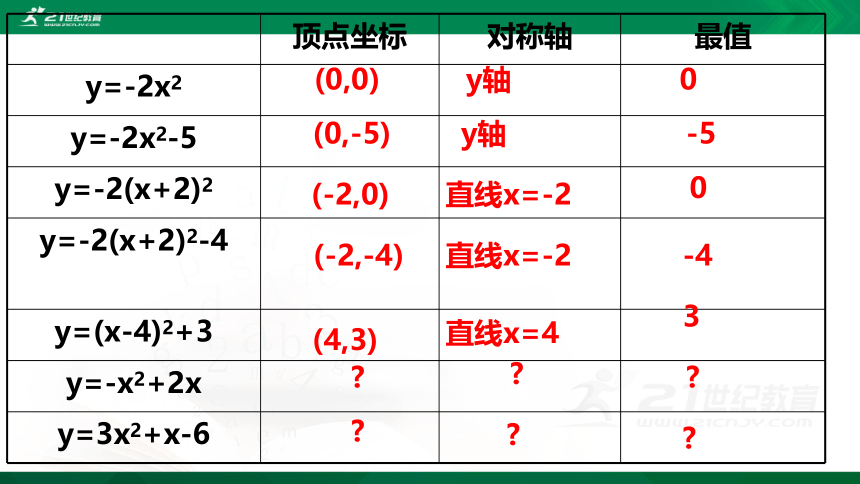
顶点坐标
对称轴
最值
y=-2x2
y=-2x2-5
y=-2(x+2)2
y=-2(x+2)2-4
y=(x-4)2+3
y=-x2+2x
y=3x2+x-6
(0,0)
y轴
0
(0,-5)
y轴
-5
(-2,0)
直线x=-2
0
(-2,-4)
直线x=-2
-4
(4,3)
直线x=4
3
?
?
?
?
?
?
探究:
如何画出y= x2-6x+21的图象呢?
我们知道,像y=a(x-h)2 +k这样的函数,容易确定相应抛物线的顶点为(h,k),二次函数y= x2-6x+21也能化成这样的形式吗?
二次函数y=ax2+bx+c与y=a(x-h)2+k之间的关系
知识点一
探究新知
y= x2-6x+21
配
方
y= (x-6)2+3.
你知道是怎样配方的吗?
3.“化”:化成顶点式.
y= (x2-12x)+21
y= (x2-12x+36-36)+21
y= (x-6) 2+21-18
y= (x-6) 2+3
1. “提”:提出二次项系数;
2.“配”:括号内配成完全平方式;
求二次函数y=ax2+bx+c的顶点式?
配方:
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为平方形式,后两项合并同类项
化简:去掉中括号
所以y=ax2+bx+c的对称轴是:
顶点坐标是:
因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1),当x<2时,y随x的增大而减小,当x>2时,y随x的增大而增大.
解:
例1 求二次函数y=2x2-8x+7图象的对称轴、顶点坐标和增减性.
例题讲解
例2 求二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
解:把二次函数y=ax2+bx+c的右边配方,得y=ax2+bx+c
例题讲解
因此,二次函数y=ax2+bx+c图象的对称轴是直
线x= ,顶点坐标是
顶点式
y=a(x-h)2 +k
二次函数y=ax2+bx+c (a ≠ 0)的图象是一条抛物线
二次函数y=ax2+bx+c的图象和性质
(1)
x
y
O
如果a>0,当x< 时,y随x的增大而减小;当x> 时,y随x的增大而增大;当x= 时,函数达到最小值,最小值为 .
(2)
x
y
O
如果a<0,当x< 时,y随x的增大而增大;当x> 时,y随x的增大而减小;当x= 时,函数达到最大值,最大值为 .
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随x的增大而减小. 在对称轴的右侧, y随x的增大而增大.
在对称轴的左侧,y随x的增大而增大. 在对称轴的右侧, y随x的增大而减小.
二次函数y=ax2+bx+c的图象和性质
知识点二
思考:1.你能画出 的图象吗?
2.如何直接画出 的图象?
3.观察图象,二次函数 的性质是什么?
如果直接画二次函数y= x2-6x+21的图象,可按如下步骤进行
由配方的结果可知,抛物线y= x2-6x+21的顶点是(6,3),对称轴是x=6.
先利用图象的对称性列表:
x
…
3
4
5
6
7
8
9
…
y=
…
7.5
5
3.5
3
3.5
5
7.5
…
然后描点画图,得到y= 的图象(如图).
从图中二次函数y= x2-6x+21的图象可以看出:在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛物线从左到右上升.也就是说,当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大.
二次函数y=ax2 +bx+c的图形与a,b,c之间的关系
知识点三
项目
字母
字母的符号
图象的特征
a
a>0
开口向上
a<0
开口向下
b
ab>0(a,b同号)
对称轴在y轴左侧
ab<0(a,b异号)
对称轴在y轴右侧
c
c=0
图象过原点
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
例3 已知二次函数y=ax2+bx+c 的图象如图,有下列结论:
① a+b+c<0;② a-b+c>0;③ abc>0;④ b=2a. 其中正确的结论有( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
B
总结:当x=1 时,对应的函数值y=ax2+bx+c=a+b+c,观察图象可知此时抛物线上对应的点在x 轴下方,说明此时的函数值y<0,即a+b+c<0.
例题讲解
1.若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位长度,再沿铅直方向向上平移三个单位,则原抛物线的表达式应变为( )
A.y=(x-2)2+3 B.y=(x-2)2+5
C.y=x2-1 D.y=x2+4
课堂练习
2.在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的表达式是( )
A. B.
C. D.
3 对于二次函数y=- x2+x-4,下列说法正确的是( )
A.当x>0时,y随x的增大而增大
B.当x=2时,y有最大值-3
C.图象的顶点坐标为(-2,-7)
D.图象与x轴有两个交点
4. 在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图所示,下列说法正确的是( )
A.abc<0,b2-4ac>0
B.abc>0,b2-4ac>0
C.abc<0,b2-4ac<0
D.abc>0,b2-4ac<0
5.二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列四个结论:①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).其中结论正确的个数是( )
A.1 B.2
C.3 D.4
二次函数y=ax2+bx+c的图象与性质
开口方向:当a>0时,开口向上;
当a<0时,开口向下;
顶点坐标:
对称轴:直线x=-
课堂小结
函数
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
增减性
当x<- 时,y随x的增大而减小;
当x>- 时,y随x的增大而增大
当x<- 时,y随x的增大而增大;
当x>- 时,y随x的增大而减小
最值
当x=- 时,y有最小
值,为
当x=- 时,y有最大
值,为
谢谢聆听
(第5课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
2.能够利用二次函数的对称轴和顶点坐标公式解决一些数学问题.
1.经历探索y=ax2+bx+c的图象特征,会用配方法求其对称轴、顶点坐标公式.
学习目标
二次函数y=a(x-h)2+k的性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
(h,k)
(h,k)
直线x=h
向上
向下
当x=h时,y有最小值为k.
当x=h时, y有最大值为k.
当x
根据图象填表:
直线x=h
当x
y=a(x-h)2+k(a<0)
y=a(x-h)2+k(a>0)
新课导入
顶点坐标
对称轴
最值
y=-2x2
y=-2x2-5
y=-2(x+2)2
y=-2(x+2)2-4
y=(x-4)2+3
y=-x2+2x
y=3x2+x-6
(0,0)
y轴
0
(0,-5)
y轴
-5
(-2,0)
直线x=-2
0
(-2,-4)
直线x=-2
-4
(4,3)
直线x=4
3
?
?
?
?
?
?
探究:
如何画出y= x2-6x+21的图象呢?
我们知道,像y=a(x-h)2 +k这样的函数,容易确定相应抛物线的顶点为(h,k),二次函数y= x2-6x+21也能化成这样的形式吗?
二次函数y=ax2+bx+c与y=a(x-h)2+k之间的关系
知识点一
探究新知
y= x2-6x+21
配
方
y= (x-6)2+3.
你知道是怎样配方的吗?
3.“化”:化成顶点式.
y= (x2-12x)+21
y= (x2-12x+36-36)+21
y= (x-6) 2+21-18
y= (x-6) 2+3
1. “提”:提出二次项系数;
2.“配”:括号内配成完全平方式;
求二次函数y=ax2+bx+c的顶点式?
配方:
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为平方形式,后两项合并同类项
化简:去掉中括号
所以y=ax2+bx+c的对称轴是:
顶点坐标是:
因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1),当x<2时,y随x的增大而减小,当x>2时,y随x的增大而增大.
解:
例1 求二次函数y=2x2-8x+7图象的对称轴、顶点坐标和增减性.
例题讲解
例2 求二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
解:把二次函数y=ax2+bx+c的右边配方,得y=ax2+bx+c
例题讲解
因此,二次函数y=ax2+bx+c图象的对称轴是直
线x= ,顶点坐标是
顶点式
y=a(x-h)2 +k
二次函数y=ax2+bx+c (a ≠ 0)的图象是一条抛物线
二次函数y=ax2+bx+c的图象和性质
(1)
x
y
O
如果a>0,当x< 时,y随x的增大而减小;当x> 时,y随x的增大而增大;当x= 时,函数达到最小值,最小值为 .
(2)
x
y
O
如果a<0,当x< 时,y随x的增大而增大;当x> 时,y随x的增大而减小;当x= 时,函数达到最大值,最大值为 .
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随x的增大而减小. 在对称轴的右侧, y随x的增大而增大.
在对称轴的左侧,y随x的增大而增大. 在对称轴的右侧, y随x的增大而减小.
二次函数y=ax2+bx+c的图象和性质
知识点二
思考:1.你能画出 的图象吗?
2.如何直接画出 的图象?
3.观察图象,二次函数 的性质是什么?
如果直接画二次函数y= x2-6x+21的图象,可按如下步骤进行
由配方的结果可知,抛物线y= x2-6x+21的顶点是(6,3),对称轴是x=6.
先利用图象的对称性列表:
x
…
3
4
5
6
7
8
9
…
y=
…
7.5
5
3.5
3
3.5
5
7.5
…
然后描点画图,得到y= 的图象(如图).
从图中二次函数y= x2-6x+21的图象可以看出:在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛物线从左到右上升.也就是说,当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大.
二次函数y=ax2 +bx+c的图形与a,b,c之间的关系
知识点三
项目
字母
字母的符号
图象的特征
a
a>0
开口向上
a<0
开口向下
b
ab>0(a,b同号)
对称轴在y轴左侧
ab<0(a,b异号)
对称轴在y轴右侧
c
c=0
图象过原点
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
例3 已知二次函数y=ax2+bx+c 的图象如图,有下列结论:
① a+b+c<0;② a-b+c>0;③ abc>0;④ b=2a. 其中正确的结论有( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
B
总结:当x=1 时,对应的函数值y=ax2+bx+c=a+b+c,观察图象可知此时抛物线上对应的点在x 轴下方,说明此时的函数值y<0,即a+b+c<0.
例题讲解
1.若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位长度,再沿铅直方向向上平移三个单位,则原抛物线的表达式应变为( )
A.y=(x-2)2+3 B.y=(x-2)2+5
C.y=x2-1 D.y=x2+4
课堂练习
2.在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的表达式是( )
A. B.
C. D.
3 对于二次函数y=- x2+x-4,下列说法正确的是( )
A.当x>0时,y随x的增大而增大
B.当x=2时,y有最大值-3
C.图象的顶点坐标为(-2,-7)
D.图象与x轴有两个交点
4. 在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象如图所示,下列说法正确的是( )
A.abc<0,b2-4ac>0
B.abc>0,b2-4ac>0
C.abc<0,b2-4ac<0
D.abc>0,b2-4ac<0
5.二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列四个结论:①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).其中结论正确的个数是( )
A.1 B.2
C.3 D.4
二次函数y=ax2+bx+c的图象与性质
开口方向:当a>0时,开口向上;
当a<0时,开口向下;
顶点坐标:
对称轴:直线x=-
课堂小结
函数
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
增减性
当x<- 时,y随x的增大而减小;
当x>- 时,y随x的增大而增大
当x<- 时,y随x的增大而增大;
当x>- 时,y随x的增大而减小
最值
当x=- 时,y有最小
值,为
当x=- 时,y有最大
值,为
谢谢聆听
