2.2.2 二次函数的图像与性质 课件(共25张PPT)
文档属性
| 名称 | 2.2.2 二次函数的图像与性质 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 22:31:07 | ||
图片预览





文档简介
第2节 二次函数的图像与性质
(第2课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.会画二次函数y=ax2+c的图象.(难点)
2.掌握二次函数y=ax2+c的性质并会应用.(重点)
3.比较函数y=ax2与y=ax2+c的联系.
学习目标
门禁反映了图形的平移,大家还记得平移的要点吗?
羽毛球的运动轨迹可以用y=ax2的图象刻画,大家能回忆出二次函数y=x2的性质吗?
新课导入
二次函数y=ax2的图象
知识点一
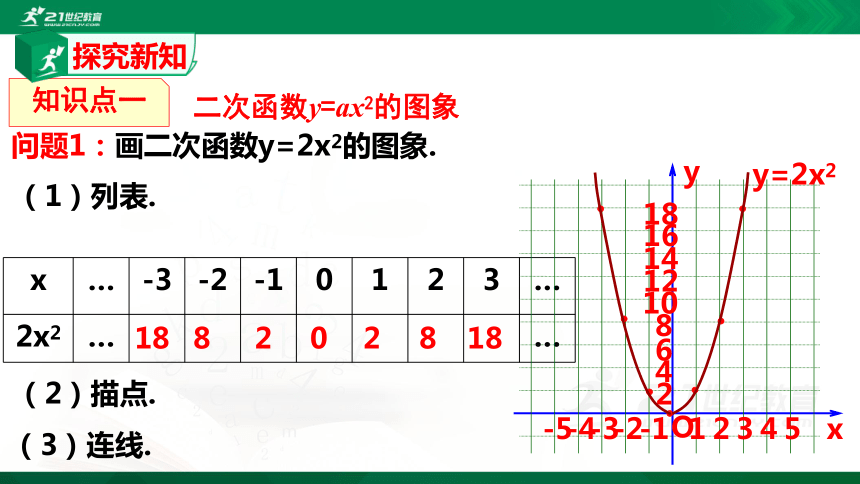
(2)描点.
(3)连线.
(1)列表.
问题1:画二次函数y=2x2的图象.
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-3
-2
-1
0
1
2
3
…
2x2
…
…
18
8
2
0
2
8
18
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2x2
探究新知
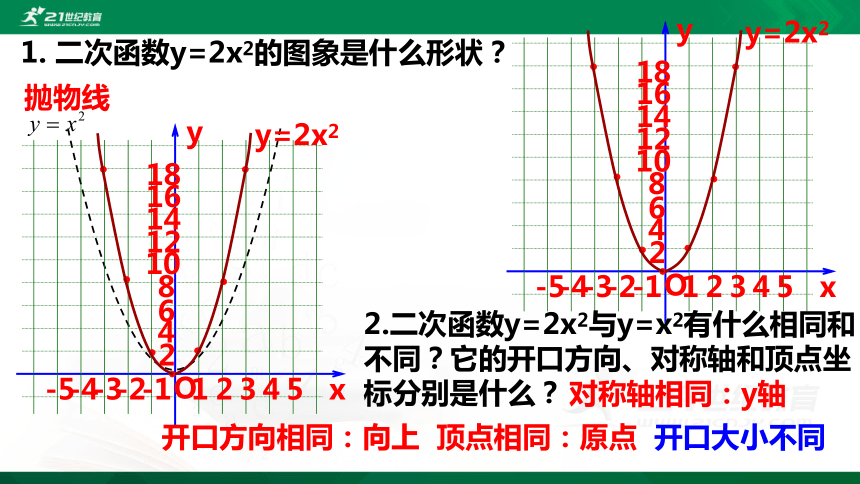
1. 二次函数y=2x2的图象是什么形状?
抛物线
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2x2
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2x2
2.二次函数y=2x2与y=x2有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
开口方向相同:向上
对称轴相同:y轴
顶点相同:原点
开口大小不同
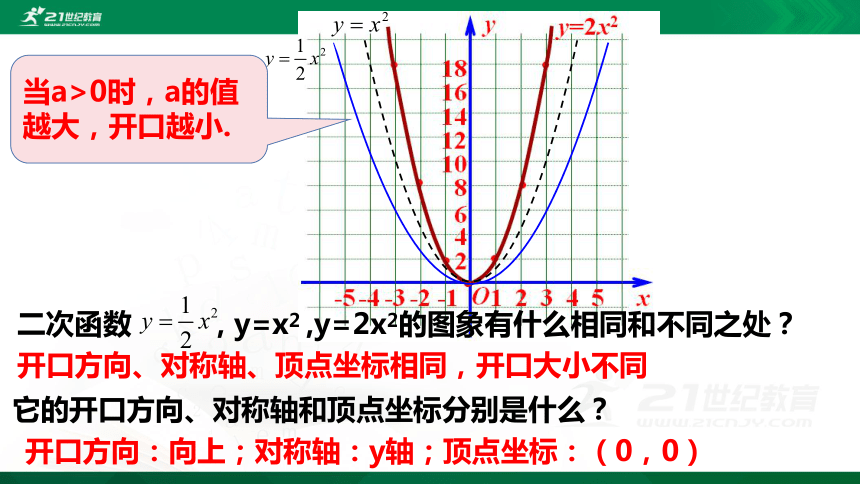
开口方向:向上;对称轴:y轴;顶点坐标:(0,0)
它的开口方向、对称轴和顶点坐标分别是什么?
开口方向、对称轴、顶点坐标相同,开口大小不同
二次函数 , y=x2 ,y=2x2的图象有什么相同和不同之处?
当a>0时,a的值越大,开口越小.
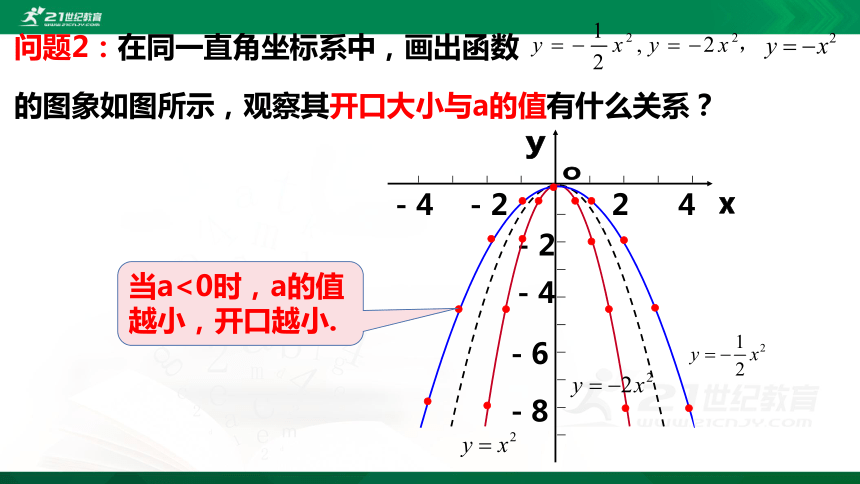
问题2:在同一直角坐标系中,画出函数
的图象如图所示,观察其开口大小与a的值有什么关系?
x
y
O
-2
2
-2
-4
-6
4
-4
-8
当a<0时,a的值越小,开口越小.
例1 在同一坐标系中画出y1=2x2,y2=-2x2和
y3= x2的图象,正确的是图中的( )
D
例题讲解
二次函数y=ax2的性质
知识点二
二次函数y=ax2(a≠0)的图象和性质如下表:
函数
y=ax2
图象
开口方向
开口大小
顶点坐标
对称轴
增减性
最值
a>0
向上
|a|越大,
开口越小
(0,0)
y轴(直线x=0)
左减
右增
当x=0时,
y最小值=0
a<0
向下
|a|越小,
开口越大
(0,0)
y轴(直线x=0)
左增
右减
当x=0时,
y最大值=0
例2 如图所示,四个二次函数的图象分别对应的是:
① y=ax2;② y=bx2;
③ y=cx2;④ y=dx 2.
①与③,②与④分别关于x 轴对称.
(1)比较a,b,c,d 的大小关系;
(2)说明a 与c,b 与d 的数量关系.
例题讲解
总结:用特殊值法:当x=1时,四个函数值分别等于二次项系数,
∴直线x=1 与四条抛物线的交点从上到下依次为
(1,a),(1,b),(1,d),(1,c),
∴ a>b>d>c.
例3 根据下列条件分别求a的取值范围:
(1)函数y=(a-2)x2,当x>0时,y随x的增大而减小,
当x<0时,y随x的增大而增大;
(2)函数y=(3a-2)x2有最大值;
(3)抛物线y=(a+2)x2与抛物线y=- x2的形状相同;
(4)函数y=axa2+a的图象是开口向上的抛物线.
例题讲解
解:(1)由题意得a-2<0,解得a<2.
(2)由题意得3a-2<0,解得a< .
(3)由题意得|a+2|= ,解得a1=- ,a2=- .
(4)由题意得a2+a=2,解得a1=-2,a2=1,
由题知a>0,∴a=1.
问题3: 画出二次函数y=2x2+1和y=2x2-1的图象,观察图象,看一看它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?
(1)列表:
x
···
-2
-1.5
-1
0
1
1.5
2
···
y=2x2+1
···
···
y=2x2-1
···
···
9
5.5
3
1
3
5.5
9
7
3.5
1
-1
1
3.5
7
(2)描点
(3)连线
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
y=2x2+1的图象是轴对称图形
开口:向上
对称轴:y轴
顶点坐标:(0,1)
y=2x2-1的图象是轴对称图形 开口:向上
对称轴:y轴 顶点坐标:(0,-1)
可以发现,把抛物线y=2x2 向 平移1个单位长度,就得到抛物线 ;把抛物线 y=2x2 向 平移1个单位长度,就得到抛物线 y=2x2-1.
下
y=2x2+1
上
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
结论:
抛物线y=ax2+c的图象相当于把抛物线y=ax2的图象 (c>0)或 (c<0)平移 个单位.
向上
向下
|c|
1.若二次函数y=ax2的图象过点P(-2,4),则该图象必经过点( )
A.(2,4) B.(-2,-4)
C.(-4,2) D.(4,-2)
课堂练习
2.函数y=ax-2与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是( )
3.函数y=k(x-k)与y=kx2,y= (k≠0)在同一平面直角坐标系中的图象可能是( )
4.抛物线y= x2,y=x2,y=-x2的共同性质是:
①都是开口向上;②都以点(0,0)为顶点;③都以y轴为对
称轴;④都关于x轴对称.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.若二次函数y=-ax2,当x=2时,y= ;则当x=-2时,y=________.
y=±x2
y=2x2
y=ax2(a>0,a<0)
y=2x2±1
y=ax2+c(c>0,c<0)
特殊
一般
分类
数形结合!
a>0开口向上 a<0开口向下|a|越大,开口越小,顶点(0,0)对称轴y轴,最值
当c>0时,向上平移|c|个单位
当c<0时,向下平移|c|个单位
课堂小结
抛物线
y=ax2(a≠0)
y= ax2 +c
开口方向
对称轴
顶点
增减性
最值
关系
y=ax2向上(下)平移|c|个单位
a>0,开口向上, a<0,开口向下
y轴
原点(0,0)
a>0时,在对称轴左侧递减,在对称轴右侧递增;a<0时,在对称轴左侧递增,在对称轴右侧递减
最大(小)值是0
最大(小)值是c
(0,c)
a>0时,在对称轴左侧递减,在对称轴右侧递增;a<0时,在对称轴左侧递增,在对称轴右侧递减
谢谢聆听
(第2课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.会画二次函数y=ax2+c的图象.(难点)
2.掌握二次函数y=ax2+c的性质并会应用.(重点)
3.比较函数y=ax2与y=ax2+c的联系.
学习目标
门禁反映了图形的平移,大家还记得平移的要点吗?
羽毛球的运动轨迹可以用y=ax2的图象刻画,大家能回忆出二次函数y=x2的性质吗?
新课导入
二次函数y=ax2的图象
知识点一
(2)描点.
(3)连线.
(1)列表.
问题1:画二次函数y=2x2的图象.
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-3
-2
-1
0
1
2
3
…
2x2
…
…
18
8
2
0
2
8
18
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2x2
探究新知
1. 二次函数y=2x2的图象是什么形状?
抛物线
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2x2
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2x2
2.二次函数y=2x2与y=x2有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
开口方向相同:向上
对称轴相同:y轴
顶点相同:原点
开口大小不同
开口方向:向上;对称轴:y轴;顶点坐标:(0,0)
它的开口方向、对称轴和顶点坐标分别是什么?
开口方向、对称轴、顶点坐标相同,开口大小不同
二次函数 , y=x2 ,y=2x2的图象有什么相同和不同之处?
当a>0时,a的值越大,开口越小.
问题2:在同一直角坐标系中,画出函数
的图象如图所示,观察其开口大小与a的值有什么关系?
x
y
O
-2
2
-2
-4
-6
4
-4
-8
当a<0时,a的值越小,开口越小.
例1 在同一坐标系中画出y1=2x2,y2=-2x2和
y3= x2的图象,正确的是图中的( )
D
例题讲解
二次函数y=ax2的性质
知识点二
二次函数y=ax2(a≠0)的图象和性质如下表:
函数
y=ax2
图象
开口方向
开口大小
顶点坐标
对称轴
增减性
最值
a>0
向上
|a|越大,
开口越小
(0,0)
y轴(直线x=0)
左减
右增
当x=0时,
y最小值=0
a<0
向下
|a|越小,
开口越大
(0,0)
y轴(直线x=0)
左增
右减
当x=0时,
y最大值=0
例2 如图所示,四个二次函数的图象分别对应的是:
① y=ax2;② y=bx2;
③ y=cx2;④ y=dx 2.
①与③,②与④分别关于x 轴对称.
(1)比较a,b,c,d 的大小关系;
(2)说明a 与c,b 与d 的数量关系.
例题讲解
总结:用特殊值法:当x=1时,四个函数值分别等于二次项系数,
∴直线x=1 与四条抛物线的交点从上到下依次为
(1,a),(1,b),(1,d),(1,c),
∴ a>b>d>c.
例3 根据下列条件分别求a的取值范围:
(1)函数y=(a-2)x2,当x>0时,y随x的增大而减小,
当x<0时,y随x的增大而增大;
(2)函数y=(3a-2)x2有最大值;
(3)抛物线y=(a+2)x2与抛物线y=- x2的形状相同;
(4)函数y=axa2+a的图象是开口向上的抛物线.
例题讲解
解:(1)由题意得a-2<0,解得a<2.
(2)由题意得3a-2<0,解得a< .
(3)由题意得|a+2|= ,解得a1=- ,a2=- .
(4)由题意得a2+a=2,解得a1=-2,a2=1,
由题知a>0,∴a=1.
问题3: 画出二次函数y=2x2+1和y=2x2-1的图象,观察图象,看一看它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?
(1)列表:
x
···
-2
-1.5
-1
0
1
1.5
2
···
y=2x2+1
···
···
y=2x2-1
···
···
9
5.5
3
1
3
5.5
9
7
3.5
1
-1
1
3.5
7
(2)描点
(3)连线
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
y=2x2+1的图象是轴对称图形
开口:向上
对称轴:y轴
顶点坐标:(0,1)
y=2x2-1的图象是轴对称图形 开口:向上
对称轴:y轴 顶点坐标:(0,-1)
可以发现,把抛物线y=2x2 向 平移1个单位长度,就得到抛物线 ;把抛物线 y=2x2 向 平移1个单位长度,就得到抛物线 y=2x2-1.
下
y=2x2+1
上
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
结论:
抛物线y=ax2+c的图象相当于把抛物线y=ax2的图象 (c>0)或 (c<0)平移 个单位.
向上
向下
|c|
1.若二次函数y=ax2的图象过点P(-2,4),则该图象必经过点( )
A.(2,4) B.(-2,-4)
C.(-4,2) D.(4,-2)
课堂练习
2.函数y=ax-2与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是( )
3.函数y=k(x-k)与y=kx2,y= (k≠0)在同一平面直角坐标系中的图象可能是( )
4.抛物线y= x2,y=x2,y=-x2的共同性质是:
①都是开口向上;②都以点(0,0)为顶点;③都以y轴为对
称轴;④都关于x轴对称.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.若二次函数y=-ax2,当x=2时,y= ;则当x=-2时,y=________.
y=±x2
y=2x2
y=ax2(a>0,a<0)
y=2x2±1
y=ax2+c(c>0,c<0)
特殊
一般
分类
数形结合!
a>0开口向上 a<0开口向下|a|越大,开口越小,顶点(0,0)对称轴y轴,最值
当c>0时,向上平移|c|个单位
当c<0时,向下平移|c|个单位
课堂小结
抛物线
y=ax2(a≠0)
y= ax2 +c
开口方向
对称轴
顶点
增减性
最值
关系
y=ax2向上(下)平移|c|个单位
a>0,开口向上, a<0,开口向下
y轴
原点(0,0)
a>0时,在对称轴左侧递减,在对称轴右侧递增;a<0时,在对称轴左侧递增,在对称轴右侧递减
最大(小)值是0
最大(小)值是c
(0,c)
a>0时,在对称轴左侧递减,在对称轴右侧递增;a<0时,在对称轴左侧递增,在对称轴右侧递减
谢谢聆听
