2.2.1二次函数的图象与性质 课件(共23张PPT)
文档属性
| 名称 | 2.2.1二次函数的图象与性质 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 22:33:22 | ||
图片预览




文档简介
第2节 二次函数的图像与性质
(第1课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.知道二次函数的图象是一条抛物线.
2.会画二次函数y=x2与y=-x2的图象.(难点)
3.掌握二次函数y=x2与y=-x2的性质,并会灵活应用.(重点)
学习目标
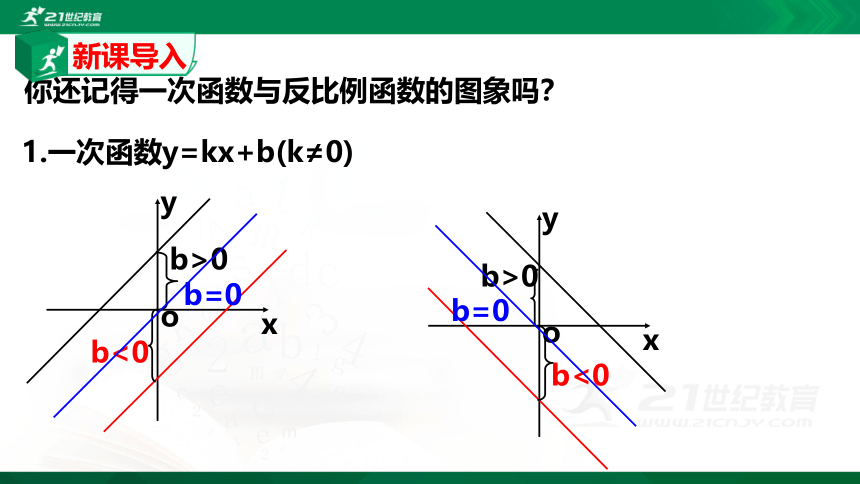
1.一次函数y=kx+b(k≠0)
x
y
o
b<0
b>0
b=0
x
y
o
b<0
b>0
b=0
你还记得一次函数与反比例函数的图象吗?
新课导入
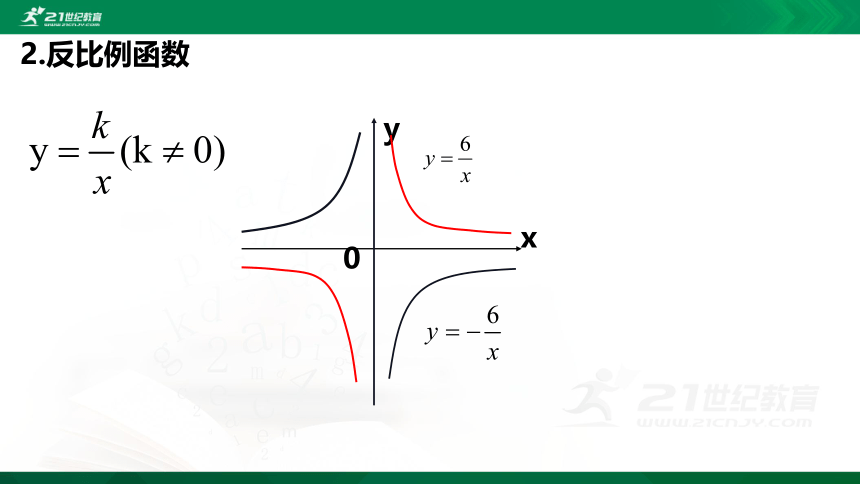
2.反比例函数
0
x
y
(1)一次函数的图象是什么?
一条直线
(2)画函数图象的基本方法与步骤是什么?
列表——描点——连线
(3)研究函数时,主要用什么来了解函数的性质呢?
主要工具是函数的图象
二次函数y=x2与y=-x2的图象
知识点一
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
…
你会用描点法画二次函数 y=x2 的图象吗?
9
4
1
0
1
9
4
1. 列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
探究新知
2
4
-2
-4
0
3
6
9
x
y
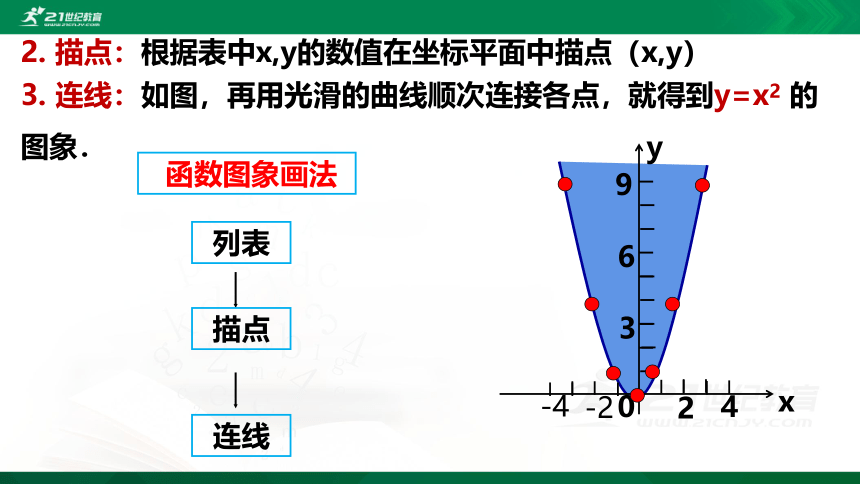
函数图象画法
列表
描点
连线
2. 描点:根据表中x,y的数值在坐标平面中描点(x,y)
3. 连线:如图,再用光滑的曲线顺次连接各点,就得到y=x2 的图象.
2
4
-2
-4
O
3
6
9
x
y
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
9
4
1
0
1
4
9
…
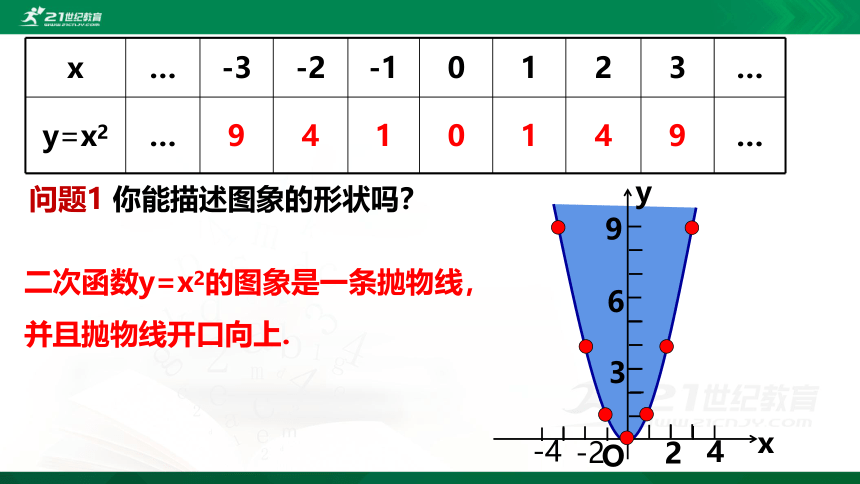
问题1 你能描述图象的形状吗?
二次函数y=x2的图象是一条抛物线,
并且抛物线开口向上.
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
2
4
-2
-4
O
3
6
9
x
y
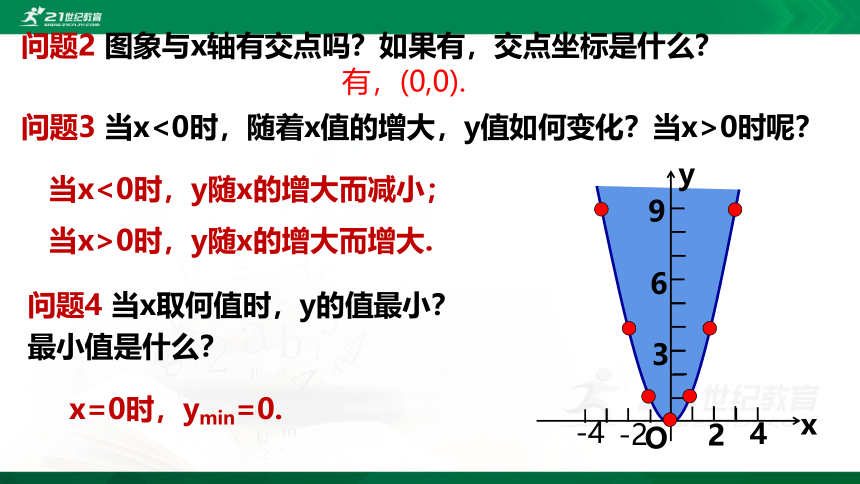
问题2 图象与x轴有交点吗?如果有,交点坐标是什么?
有,(0,0).
问题3 当x<0时,随着x值的增大,y值如何变化?当x>0时呢?
问题4 当x取何值时,y的值最小?
最小值是什么?
x=0时,ymin=0.
-3
3
o
3
6
9
x
y
对称轴与抛物线的交
点叫做抛物线的顶点,
它是图象的最低点,
为(0,0).
问题5 图象是轴对称图形吗?如果是,它的对称轴是什么?
这条抛物线关于y轴对称,
y轴就是它的对称轴.
例1 画出函数y=-x2的图象,并仿照y=x2的性质说出y=-x2有哪些性质?
y
2
4
-2
-4
0
-3
-6
-9
x
x
…
-3
-2
-1
0
1
2
3
…
y=-x2
…
-9
-4
-1
0
-1
-4
-9
…
例题讲解
抛物线关于y轴对称.
顶点坐标是(0,0);是抛物线上的最高点.
2
4
-2
-4
0
-3
-6
-9
x
图象是一条开口向下的抛物线.
当x<0时,y随x的增大而增大;
当x>0时,y随x的增大而减小,
当x=0时,ymax=0.
二次函数y=x2与y=-x2的性质
知识点二
议一议
观察二次函数y=x2与 y =-x2的图象,你能发现什么问题?
抛物线
y=x2
y=-x2
顶点坐标
对称轴
位置
开口方向
极值
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方(除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
例2 抛物线y=x2,y=-x2 的共同性质是:
①都是开口向上; ②都以点(0,0)为顶点;③都以y 轴为对称轴; ④都关于x 轴对称.其中正确的有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
例题讲解
例3 已知 是二次函数,且当x>0时,y随x
的增大而减小,则a=________.
解析:由题意可知
解得a=3或a=-3.
又∵当x>0时,y随x的增大而减小,
∴a=3.
3
例题讲解
1.已知正方形的边长为x(cm),则它的面积y(cm2)与边长x(cm)的函数关系图象为( )
课堂练习
2.关于y=x2与y=-x2的图象,下列说法中错误的是( )
A.其形状相同,但开口方向相反,原因是函数表达式的系数互为相反数
B.都关于y轴对称
C.图象都有最低点,且其坐标均为(0,0)
D.两图象关于x轴对称
3.如图,一次函数y1=kx+b的图象与二次函数y2=x2的图象交于A(-1,1)和B(2,4)两点,则当y1A.x<-1
B.x>2
C.-1D.x<-1或x>2
4.已知点(x1,y1),(x2,y2)是二次函数y=-x2的图象上的两点,当x15.若 是二次函数,且开口向上,则m值
是_____.
函数
图像
开口方向
顶点
坐标
对称轴
函数变化
最值
a>0
a<0
二次函数y=ax2的图像和性质
向上
向下
(0,0)
(0,0)
y轴
y轴
当X=0时
y有最小值y最小=0
当X=0时
y有最大
值y最大=0
当x<0时,y随x的增大而增大;
当x>0时,y随x的增大而减小;
y=ax2
当x<0时,y随x的增大而减小;
当x>0时,y随x的增大而增大;
抛物线
x
y
o
抛物线
x
y
o
y=ax2
课堂小结
谢谢聆听
(第1课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.知道二次函数的图象是一条抛物线.
2.会画二次函数y=x2与y=-x2的图象.(难点)
3.掌握二次函数y=x2与y=-x2的性质,并会灵活应用.(重点)
学习目标
1.一次函数y=kx+b(k≠0)
x
y
o
b<0
b>0
b=0
x
y
o
b<0
b>0
b=0
你还记得一次函数与反比例函数的图象吗?
新课导入
2.反比例函数
0
x
y
(1)一次函数的图象是什么?
一条直线
(2)画函数图象的基本方法与步骤是什么?
列表——描点——连线
(3)研究函数时,主要用什么来了解函数的性质呢?
主要工具是函数的图象
二次函数y=x2与y=-x2的图象
知识点一
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
…
你会用描点法画二次函数 y=x2 的图象吗?
9
4
1
0
1
9
4
1. 列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
探究新知
2
4
-2
-4
0
3
6
9
x
y
函数图象画法
列表
描点
连线
2. 描点:根据表中x,y的数值在坐标平面中描点(x,y)
3. 连线:如图,再用光滑的曲线顺次连接各点,就得到y=x2 的图象.
2
4
-2
-4
O
3
6
9
x
y
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
9
4
1
0
1
4
9
…
问题1 你能描述图象的形状吗?
二次函数y=x2的图象是一条抛物线,
并且抛物线开口向上.
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
2
4
-2
-4
O
3
6
9
x
y
问题2 图象与x轴有交点吗?如果有,交点坐标是什么?
有,(0,0).
问题3 当x<0时,随着x值的增大,y值如何变化?当x>0时呢?
问题4 当x取何值时,y的值最小?
最小值是什么?
x=0时,ymin=0.
-3
3
o
3
6
9
x
y
对称轴与抛物线的交
点叫做抛物线的顶点,
它是图象的最低点,
为(0,0).
问题5 图象是轴对称图形吗?如果是,它的对称轴是什么?
这条抛物线关于y轴对称,
y轴就是它的对称轴.
例1 画出函数y=-x2的图象,并仿照y=x2的性质说出y=-x2有哪些性质?
y
2
4
-2
-4
0
-3
-6
-9
x
x
…
-3
-2
-1
0
1
2
3
…
y=-x2
…
-9
-4
-1
0
-1
-4
-9
…
例题讲解
抛物线关于y轴对称.
顶点坐标是(0,0);是抛物线上的最高点.
2
4
-2
-4
0
-3
-6
-9
x
图象是一条开口向下的抛物线.
当x<0时,y随x的增大而增大;
当x>0时,y随x的增大而减小,
当x=0时,ymax=0.
二次函数y=x2与y=-x2的性质
知识点二
议一议
观察二次函数y=x2与 y =-x2的图象,你能发现什么问题?
抛物线
y=x2
y=-x2
顶点坐标
对称轴
位置
开口方向
极值
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方(除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
例2 抛物线y=x2,y=-x2 的共同性质是:
①都是开口向上; ②都以点(0,0)为顶点;③都以y 轴为对称轴; ④都关于x 轴对称.其中正确的有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
例题讲解
例3 已知 是二次函数,且当x>0时,y随x
的增大而减小,则a=________.
解析:由题意可知
解得a=3或a=-3.
又∵当x>0时,y随x的增大而减小,
∴a=3.
3
例题讲解
1.已知正方形的边长为x(cm),则它的面积y(cm2)与边长x(cm)的函数关系图象为( )
课堂练习
2.关于y=x2与y=-x2的图象,下列说法中错误的是( )
A.其形状相同,但开口方向相反,原因是函数表达式的系数互为相反数
B.都关于y轴对称
C.图象都有最低点,且其坐标均为(0,0)
D.两图象关于x轴对称
3.如图,一次函数y1=kx+b的图象与二次函数y2=x2的图象交于A(-1,1)和B(2,4)两点,则当y1
B.x>2
C.-1
4.已知点(x1,y1),(x2,y2)是二次函数y=-x2的图象上的两点,当x1
是_____.
函数
图像
开口方向
顶点
坐标
对称轴
函数变化
最值
a>0
a<0
二次函数y=ax2的图像和性质
向上
向下
(0,0)
(0,0)
y轴
y轴
当X=0时
y有最小值y最小=0
当X=0时
y有最大
值y最大=0
当x<0时,y随x的增大而增大;
当x>0时,y随x的增大而减小;
y=ax2
当x<0时,y随x的增大而减小;
当x>0时,y随x的增大而增大;
抛物线
x
y
o
抛物线
x
y
o
y=ax2
课堂小结
谢谢聆听
