四年级下册数学课件-第2单元 3.探索与发现:三角形内角和 北师大版(共19张PPT)
文档属性
| 名称 | 四年级下册数学课件-第2单元 3.探索与发现:三角形内角和 北师大版(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 06:33:10 | ||
图片预览

文档简介
北师大版四年级下册
三角形内角和
激趣导入
他们在争论什么?
他说的对吗?
我的三个内角的和一定比你大。
是这样吗?
探究新知
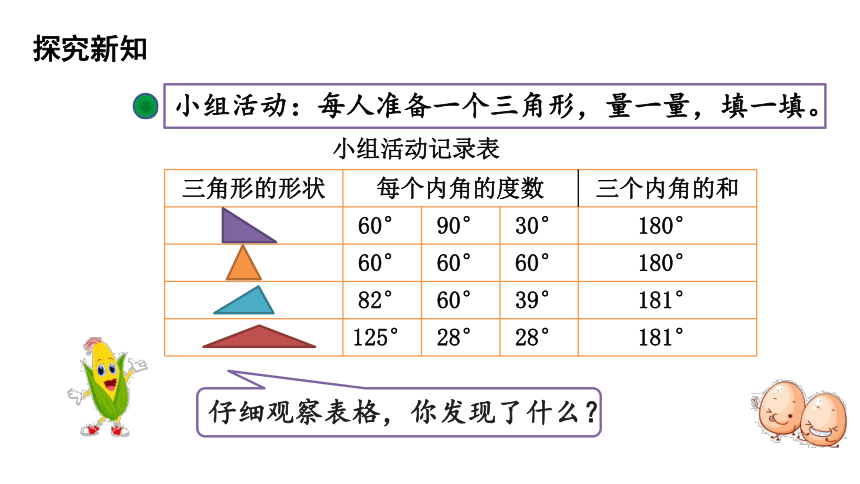
小组活动:每人准备一个三角形,量一量,填一填。
仔细观察表格,你发现了什么?
小组活动记录表
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}三角形的形状
每个内角的度数
三个内角的和
60°
90°
30°
180°
60°
60°
60°
180°
82°
60°
39°
181°
125°
28°
28°
181°
探究新知
你发现了什么?
我发现每个三角形的内角和都在180°左右。
实际上,三角形内角和就是180°,只是因为测量有误差,才影响内角和的准确。
探究新知
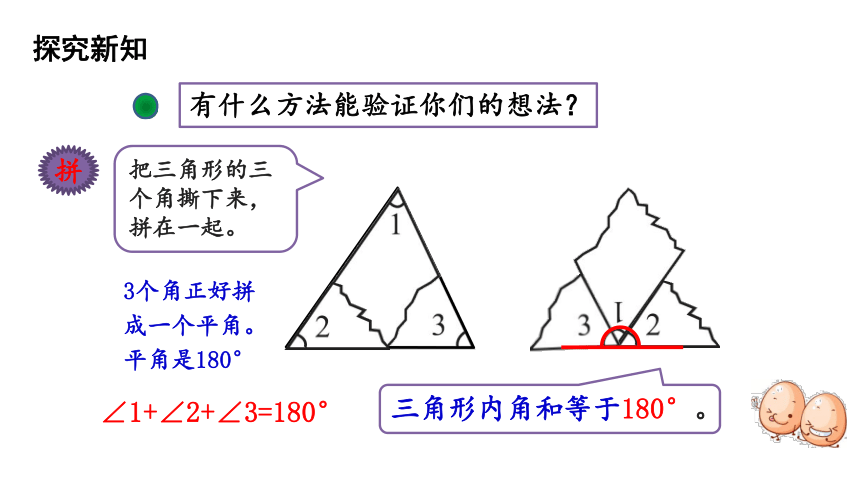
有什么方法能验证你们的想法?
把三角形的三个角撕下来,拼在一起。
三角形内角和等于180°。
拼
3个角正好拼成一个平角。平角是180°
∠1+∠2+∠3=180°
探究新知
有什么方法能验证你们的想法?
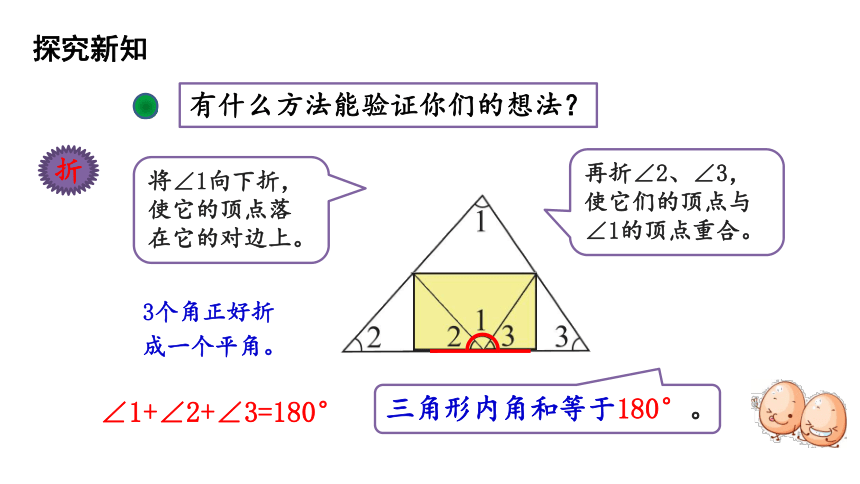
将∠1向下折,使它的顶点落在它的对边上。
折
再折∠2、∠3,使它们的顶点与∠1的顶点重合。
3个角正好折成一个平角。
三角形内角和等于180°。
∠1+∠2+∠3=180°
探究新知
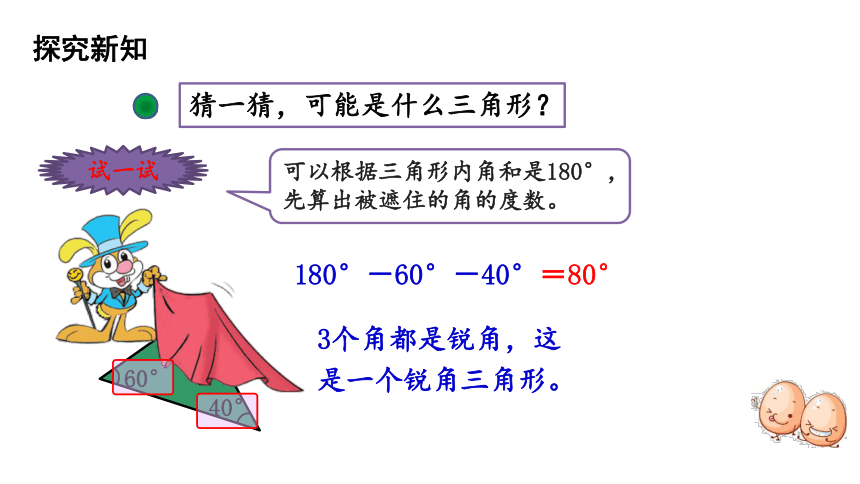
猜一猜,可能是什么三角形?
试一试
可以根据三角形内角和是180°,先算出被遮住的角的度数。
3个角都是锐角,这是一个锐角三角形。
180°-60°-40°=80°
60°
40°
80°
探究新知
你还能猜出是什么三角形?
试一试
等边三角形每个角都是60°。
可能是等边三角形。
180°-60°=120°
剩下两个角度数和:
探究新知
你还能猜出是什么三角形?
试一试
如果一个角是100°。
可能是钝角三角形。
180°-60° - 100°=20°
另一个角:
探究新知
你还能猜出是什么三角形?
试一试
如果一个角是90°。
可能是直角三角形。
180°-60° - 90°=30°
另一个角:
还有可能是什么三角形呢?
巩固练习
填出下面各角的度数。
77°
180°- 75° - 28°=87°
75°
28°
A
B
C
45°
20°
A
B
C
∠B=_____
∠C=_____
∠A=____
35°
C
A
B
85°
60°
115°
巩固练习
填空。
直角三角形的一个锐角是20°,另一个锐角是
( )°度。
直角三角形的一个锐角是54°,另一个锐角是
( )°度。
70
36
90° - 20°=70°
巩固练习
它们说的对吗?
不对,因为这是一个钝角三角形,其中一个角大于90°小于180°,而三角形内角和是180°,所以另外两个锐角之和要小于90°。
我的两个锐角之和大于90°。
我的两个锐角之和正好等于90°。
钝角
巩固练习
它们说的对吗?
第2种说法对,因为这是一个直角三角形,其中一个角是90°,所以另外两个锐角之和等于90°。
我的两个锐角之和大于90°。
我的两个锐角之和正好等于90°。
直角
巩固练习
选择。
一个三角形有两个角是锐角,则第三个角是( )。
A.一定是锐角 B.一定是钝角
C.一定是直角 D.可能是锐角或直角或钝角
D
巩固练习
所有三角形内角和都是180°。
下列说法对吗。
大三角形的内角和比小三角形的内角和大。( )
一个三角形中最多只能有一个直角。( )
×
√
归纳总结
三角形内角和
三角形内角和等于180°,根据内角和度数和其中两个角的度数,可以求出另外一个角的度数。
课堂作业
课堂作业:
26页第7题
谢谢大家
三角形内角和
激趣导入
他们在争论什么?
他说的对吗?
我的三个内角的和一定比你大。
是这样吗?
探究新知
小组活动:每人准备一个三角形,量一量,填一填。
仔细观察表格,你发现了什么?
小组活动记录表
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}三角形的形状
每个内角的度数
三个内角的和
60°
90°
30°
180°
60°
60°
60°
180°
82°
60°
39°
181°
125°
28°
28°
181°
探究新知
你发现了什么?
我发现每个三角形的内角和都在180°左右。
实际上,三角形内角和就是180°,只是因为测量有误差,才影响内角和的准确。
探究新知
有什么方法能验证你们的想法?
把三角形的三个角撕下来,拼在一起。
三角形内角和等于180°。
拼
3个角正好拼成一个平角。平角是180°
∠1+∠2+∠3=180°
探究新知
有什么方法能验证你们的想法?
将∠1向下折,使它的顶点落在它的对边上。
折
再折∠2、∠3,使它们的顶点与∠1的顶点重合。
3个角正好折成一个平角。
三角形内角和等于180°。
∠1+∠2+∠3=180°
探究新知
猜一猜,可能是什么三角形?
试一试
可以根据三角形内角和是180°,先算出被遮住的角的度数。
3个角都是锐角,这是一个锐角三角形。
180°-60°-40°=80°
60°
40°
80°
探究新知
你还能猜出是什么三角形?
试一试
等边三角形每个角都是60°。
可能是等边三角形。
180°-60°=120°
剩下两个角度数和:
探究新知
你还能猜出是什么三角形?
试一试
如果一个角是100°。
可能是钝角三角形。
180°-60° - 100°=20°
另一个角:
探究新知
你还能猜出是什么三角形?
试一试
如果一个角是90°。
可能是直角三角形。
180°-60° - 90°=30°
另一个角:
还有可能是什么三角形呢?
巩固练习
填出下面各角的度数。
77°
180°- 75° - 28°=87°
75°
28°
A
B
C
45°
20°
A
B
C
∠B=_____
∠C=_____
∠A=____
35°
C
A
B
85°
60°
115°
巩固练习
填空。
直角三角形的一个锐角是20°,另一个锐角是
( )°度。
直角三角形的一个锐角是54°,另一个锐角是
( )°度。
70
36
90° - 20°=70°
巩固练习
它们说的对吗?
不对,因为这是一个钝角三角形,其中一个角大于90°小于180°,而三角形内角和是180°,所以另外两个锐角之和要小于90°。
我的两个锐角之和大于90°。
我的两个锐角之和正好等于90°。
钝角
巩固练习
它们说的对吗?
第2种说法对,因为这是一个直角三角形,其中一个角是90°,所以另外两个锐角之和等于90°。
我的两个锐角之和大于90°。
我的两个锐角之和正好等于90°。
直角
巩固练习
选择。
一个三角形有两个角是锐角,则第三个角是( )。
A.一定是锐角 B.一定是钝角
C.一定是直角 D.可能是锐角或直角或钝角
D
巩固练习
所有三角形内角和都是180°。
下列说法对吗。
大三角形的内角和比小三角形的内角和大。( )
一个三角形中最多只能有一个直角。( )
×
√
归纳总结
三角形内角和
三角形内角和等于180°,根据内角和度数和其中两个角的度数,可以求出另外一个角的度数。
课堂作业
课堂作业:
26页第7题
谢谢大家
