2.5 二次函数与一元二次方程(第2课时)由图象判断根 课件(共13张PPT)
文档属性
| 名称 | 2.5 二次函数与一元二次方程(第2课时)由图象判断根 课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 20:53:12 | ||
图片预览




文档简介
数学北师大版
九年级
2.5二次函数与一元二次方程第2课时由图象判断根
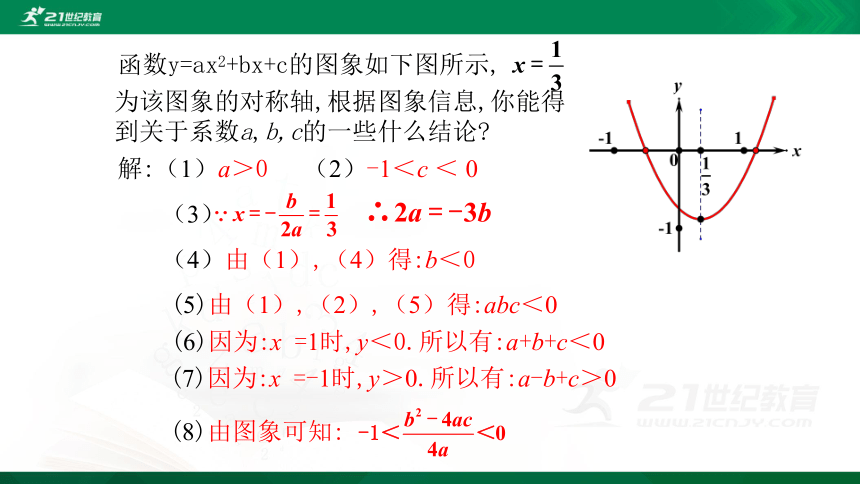
函数y=ax2+bx+c的图象如下图所示,
为该图象的对称轴,根据图象信息,你能得到关于系数a,b,c的一些什么结论?
解:(1)a>0
(2)-1<c < 0
(4)由(1),(4)得:b<0
(5)由(1),(2),(5)得:abc<0
(6)因为:x =1时,y<0.所以有:a+b+c<0
(7)因为:x =-1时,y>0.所以有:a-b+c>0
(8)由图象可知:
(3)
(1).用描点法作二次函数y=x2+2x-10的图象;
你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗?
(2).观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间
1.先求-5和-4之间的根,利用计算器进行探索
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-4.1
-4.2
-4.3
-4.4
y
-1.39
-0.76
-0.11
0.56
-0.11最与0接近,所以x1≈-4.3
(2).观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间
(3).确定方程x2+2x-10=0的解;
由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
2.再求2和3之间的根,利用计算器进行探索
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
2.1
2.2
2.3
2.4
y
-1.39
-0.76
-0.11
0.56
所以x2≈2.3
验证x 2+2x -10=0的解是x =
即得x1≈-4.3,x2≈2.3.
做一做
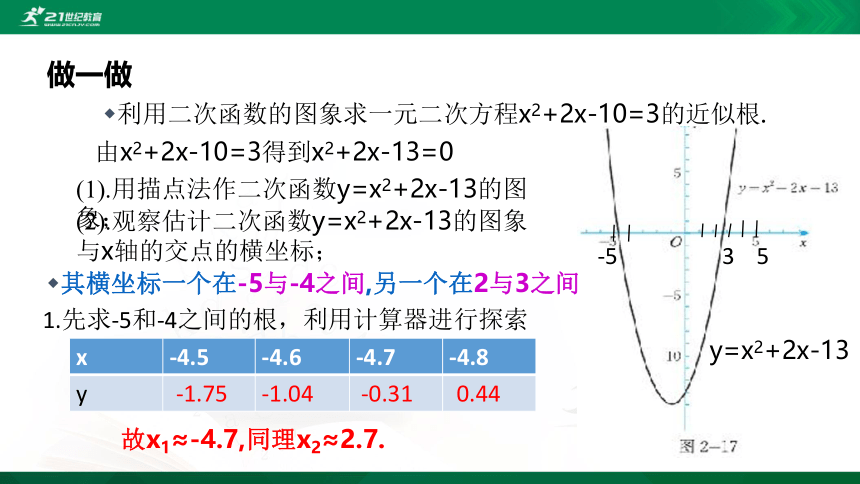
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
由x2+2x-10=3得到x2+2x-13=0
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-4.5
-4.6
-4.7
-4.8
y
(1).用描点法作二次函数y=x2+2x-13的图象;
(2).观察估计二次函数y=x2+2x-13的图象与x轴的交点的横坐标;
其横坐标一个在-5与-4之间,另一个在2与3之间
1.先求-5和-4之间的根,利用计算器进行探索
y=x2+2x-13
3
5
-5
-1.75
-1.04
-0.31
0.44
故x1≈-4.7,同理x2≈2.7.
比较这二个图形
y=x2+2x-13
y=x2+2x-10
第一个图形向上移3个单位或者把x轴向下移3个单位
便得到第二图形,或者把x轴向下移3个单位。
第二个图形向下移3个单位或者把x轴向上移3个单位
便得到第二图形,或者把x轴向下移3个单位。
利用右图二次函数的图象求一元二次方程x2+2x-10=3的近似根.
分析只要把y=x2+2x-10的二次函数的x轴向上移动三个单位,即移到y=3处便得到y=x2+2x-13的二次函数图象。
y=x2+2x-13的二次函数图象与x轴的交点,就是y=x2+2x-10与y=3的交点。
y=x2+2x-10
y=3
由图象知y=x2+2x-10与y=3的交点的横坐标
一个在-5和-4之间,另一个在2和3之间。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-4.5
-4.6
-4.7
-4.8
y
1.25
1.96
2.69
3.44
2.69最接近3,故x1=-4.7同理x2=2.7
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
就是把方程x2+2x-10=3分成二个二次函数(等式左边
一个二次函数右边一个二次函数)它们相交的交点的
横坐标就是该方程的解。
知识拓展、迁移运用
例题:利用图象解一元二次方程x2+x-3=0时,我们采用的一种方法是:x2+x-3=0变形x2=-x+3在平面直角坐标系中画出抛物线y=x2和直线y=-x+3,两图象交点的横坐标就是该方程的解.
由图象可得,方程 的近似解为:x1=-1.4,x2=4.4.
练习:
利用图象求方程 的近似解.
如图画出y1和y2的图
利用二次函数y=ax2+bx+c的图象求一元二次方
程ax2+bx+c=0的近似根的一般步骤是怎样的?
课堂小结
①用描点法作二次函数y=ax2+bx+c的图象;
②观察估计二次函数的图象与x轴的交点的横坐标;
③确定一元二次方程ax2+bx+c=0的解。
二次函数y=-2x2+4x+1的图象如图所示,求一元二次方程-2x2+4x+1=0的近似根.
(1).观察估计二次函数y=-2x2+4x+1的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-1与0之间,另一个在2与3之间,分别约为-0.2和2.2(可将单位长再十等分,借助计算器确定其近似值).
(3).确定方程-2x2+4x+1=0的解;
由此可知,方程-2x2+4x+1=0的近似根为:x1≈-0.2,x2≈2.2.
课堂练习
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
九年级
2.5二次函数与一元二次方程第2课时由图象判断根
函数y=ax2+bx+c的图象如下图所示,
为该图象的对称轴,根据图象信息,你能得到关于系数a,b,c的一些什么结论?
解:(1)a>0
(2)-1<c < 0
(4)由(1),(4)得:b<0
(5)由(1),(2),(5)得:abc<0
(6)因为:x =1时,y<0.所以有:a+b+c<0
(7)因为:x =-1时,y>0.所以有:a-b+c>0
(8)由图象可知:
(3)
(1).用描点法作二次函数y=x2+2x-10的图象;
你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗?
(2).观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间
1.先求-5和-4之间的根,利用计算器进行探索
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-4.1
-4.2
-4.3
-4.4
y
-1.39
-0.76
-0.11
0.56
-0.11最与0接近,所以x1≈-4.3
(2).观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间
(3).确定方程x2+2x-10=0的解;
由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
2.再求2和3之间的根,利用计算器进行探索
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
2.1
2.2
2.3
2.4
y
-1.39
-0.76
-0.11
0.56
所以x2≈2.3
验证x 2+2x -10=0的解是x =
即得x1≈-4.3,x2≈2.3.
做一做
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
由x2+2x-10=3得到x2+2x-13=0
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-4.5
-4.6
-4.7
-4.8
y
(1).用描点法作二次函数y=x2+2x-13的图象;
(2).观察估计二次函数y=x2+2x-13的图象与x轴的交点的横坐标;
其横坐标一个在-5与-4之间,另一个在2与3之间
1.先求-5和-4之间的根,利用计算器进行探索
y=x2+2x-13
3
5
-5
-1.75
-1.04
-0.31
0.44
故x1≈-4.7,同理x2≈2.7.
比较这二个图形
y=x2+2x-13
y=x2+2x-10
第一个图形向上移3个单位或者把x轴向下移3个单位
便得到第二图形,或者把x轴向下移3个单位。
第二个图形向下移3个单位或者把x轴向上移3个单位
便得到第二图形,或者把x轴向下移3个单位。
利用右图二次函数的图象求一元二次方程x2+2x-10=3的近似根.
分析只要把y=x2+2x-10的二次函数的x轴向上移动三个单位,即移到y=3处便得到y=x2+2x-13的二次函数图象。
y=x2+2x-13的二次函数图象与x轴的交点,就是y=x2+2x-10与y=3的交点。
y=x2+2x-10
y=3
由图象知y=x2+2x-10与y=3的交点的横坐标
一个在-5和-4之间,另一个在2和3之间。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-4.5
-4.6
-4.7
-4.8
y
1.25
1.96
2.69
3.44
2.69最接近3,故x1=-4.7同理x2=2.7
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
就是把方程x2+2x-10=3分成二个二次函数(等式左边
一个二次函数右边一个二次函数)它们相交的交点的
横坐标就是该方程的解。
知识拓展、迁移运用
例题:利用图象解一元二次方程x2+x-3=0时,我们采用的一种方法是:x2+x-3=0变形x2=-x+3在平面直角坐标系中画出抛物线y=x2和直线y=-x+3,两图象交点的横坐标就是该方程的解.
由图象可得,方程 的近似解为:x1=-1.4,x2=4.4.
练习:
利用图象求方程 的近似解.
如图画出y1和y2的图
利用二次函数y=ax2+bx+c的图象求一元二次方
程ax2+bx+c=0的近似根的一般步骤是怎样的?
课堂小结
①用描点法作二次函数y=ax2+bx+c的图象;
②观察估计二次函数的图象与x轴的交点的横坐标;
③确定一元二次方程ax2+bx+c=0的解。
二次函数y=-2x2+4x+1的图象如图所示,求一元二次方程-2x2+4x+1=0的近似根.
(1).观察估计二次函数y=-2x2+4x+1的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-1与0之间,另一个在2与3之间,分别约为-0.2和2.2(可将单位长再十等分,借助计算器确定其近似值).
(3).确定方程-2x2+4x+1=0的解;
由此可知,方程-2x2+4x+1=0的近似根为:x1≈-0.2,x2≈2.2.
课堂练习
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
