2021届高考数学(文)二轮专题十一 坐标系与参数方程(文) 学案Word
文档属性
| 名称 | 2021届高考数学(文)二轮专题十一 坐标系与参数方程(文) 学案Word |  | |
| 格式 | docx | ||
| 文件大小 | 720.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 21:23:53 | ||
图片预览




文档简介
313690229235
38177376752专题 11
××
坐标系与参数方程
00专题 11
××
坐标系与参数方程
命题趋势
命题趋势
本部分内容主要考查极坐标方程与普通方程的互化,参数方程与普通方程的互化;已知直线或曲线的参数方程或极坐标方程,求距离、面积等综合问题,本部分考查难度一般不大.
考点清单
考点清单
1.平面直角坐标系中的伸缩变换
设点P(x,y)是平面直角坐标系中的任意一点,在变换的作用下,
点P(x,y)对应到点P'(x',y'),称为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.
2.极坐标系的概念
在平面内取一个定点O,叫做极点;自极点O引一条射线Ox叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.
点M的极坐标:设M是平面内一点,极点O与点M的距离|OM|叫做点M的极径,记为ρ;
以极轴Ox为始边,射线OM为终边的∠xOM叫做点M的极角,记为θ.
有序数对(ρ,θ)叫做点M的极坐标,记为M(ρ,θ).
一般地,不做特殊说明时,我们认为ρ≥0,θ可取任何实数.
注:极坐标(ρ,θ)与(ρ,θ+2kπ)(k∈Z)表示同一个点.极点O的坐标为(0,θ)(θ∈R).
若ρ<0,则-ρ>0,规定点(-ρ,θ)与点(ρ,θ)关于极点对称,即(-ρ,θ)与(ρ,π+θ)表示同一点.
如果规定ρ>0,0≤θ<2π,那么除极点外,平面内的点可用唯一的极坐标(ρ,θ)表示(即一一对应的关系);同时,极坐标(ρ,θ)表示的点也是唯一确定的.
极坐标与直角坐标都是一对有序实数确定平面上一个点,在极坐标系下,一对有序实数ρ、θ对应唯一点P (ρ,θ),但平面内任一个点P的极坐标不唯一.一个点可以有无数个坐标,这些坐标又有规律可循的,P (ρ,θ)(极点除外)的全部坐标为(ρ,θ+2kπ)或(-ρ,θ+(2k+1)π),(k∈Z).极点的极径为0,而极角任意取.若对ρ、θ的取值范围加以限制.
则除极点外,平面上点的极坐标就唯一了,如限定ρ>0,0≤θ<2π或ρ<0,-π<θ≤π等.
极坐标与直角坐标的不同是,直角坐标系中,点与坐标是一一对应的,而极坐标系中,点与坐标是一多对应的.
即一个点的极坐标是不唯一的.
3.极坐标与直角坐标的互化
设M是平面内任意一点,它的直角坐标是(x,y),极坐标是(ρ,θ),从图中可以得出:
,,,.
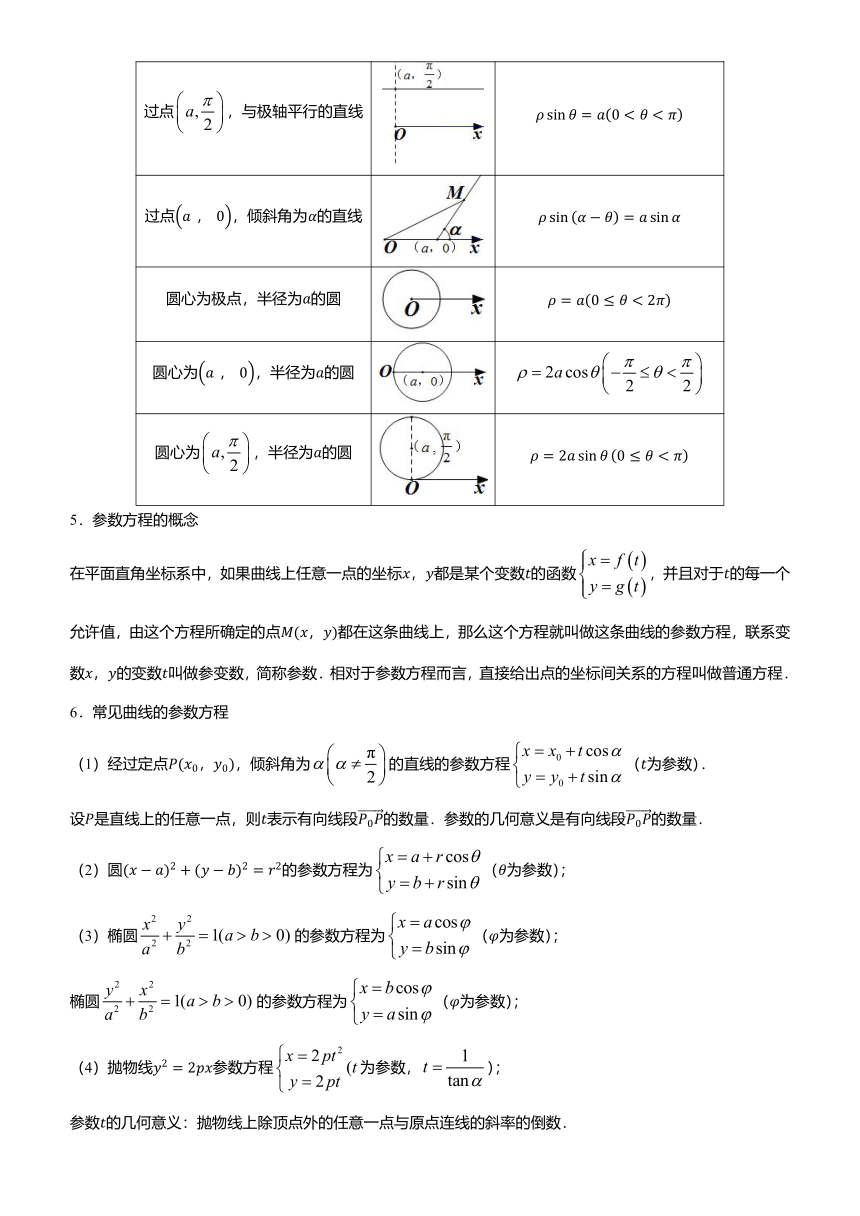
4.常见曲线的极坐标方程
曲线
图形
极坐标方程
过极点,倾斜角为α的直线
(1)θ=αρ∈R和θ=π+αρ∈R
(2)θ=α(ρ≥0)和θ=π+α(ρ≥0)
过点a?,?0,与极轴垂直的直线
ρcosθ=a
过点,与极轴平行的直线
ρsinθ=a0<θ<π
过点a?,?0,倾斜角为α的直线
ρsinα-θ=asinα
圆心为极点,半径为a的圆
ρ=a0≤θ<2π
圆心为a?,?0,半径为a的圆
圆心为,半径为a的圆
ρ=2asinθ0≤θ<π
5.参数方程的概念
在平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某个变数t的函数,并且对于t的每一个允许值,由这个方程所确定的点M(x,y)都在这条曲线上,那么这个方程就叫做这条曲线的参数方程,联系变数x,y的变数t叫做参变数,简称参数.相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.
6.常见曲线的参数方程
(1)经过定点P(x0,y0),倾斜角为的直线的参数方程(t为参数).
设P是直线上的任意一点,则t表示有向线段P0P的数量.参数的几何意义是有向线段P0P的数量.
(2)圆(x-a)2+(y-b)2=r2的参数方程为(θ为参数);
(3)椭圆的参数方程为(φ为参数);
椭圆的参数方程为(φ为参数);
(4)抛物线y2=2px参数方程为参数,);
参数t的几何意义:抛物线上除顶点外的任意一点与原点连线的斜率的倒数.
7.参数方程与普通方程之间的互化
在建立曲线的参数方程时,要注明参数及参数的取值范围.在参数方程与普通方程的互化中,
必须使x,y的取值范围保持一致.
参数方程化为普通方程的关键是消参数,并且要保证等价性.若不可避免地破坏了同解变形,
则一定要通过.根据t的取值范围导出x,y的取值范围.
精题集训
(70分钟)
精题集训
(70分钟)
经典训练题
经典训练题
一、选择题.
1.极坐标系中,若等边△ABC的两个顶点、,那么顶点C的极坐标可能是( )
A. B. C. D.
二、解答题.
2.在平面直角坐标系中,曲线C的参数方程为(θ为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)射线OP的极坐标方程为,若射线OP与曲线C的交点为A (异于点O),与直线l的交点为B,求线段AB的长.
3.在直角坐标系xOy中,直线l过点P(0,2),倾斜角为.以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos 2θ-2sinθ=0.
(1)求直线l的参数方程与曲线C的直角坐标方程;
(2)若直线l交曲线C于A,B两点,M为AB中点,且满足|PA|,|PM|,|PB|成等比数列,求直线l的斜率.
4.在直角坐标系xOy中,曲线C1的参数方程为 (α为参数).以原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)设P为曲线C1上的动点,求点P到C2的距离的最大值,并求此时点P的坐标.
5.在平面直角坐标系xOy中,曲线C的参数方程为 (m为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)若直线l与曲线C相交于点P,求圆心在极轴上,且经过极点和点P的圆的直角坐标方程.
6.在平面直角坐标系xOy中,曲线C1的参数方程为(θ为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为.
(1)求C1的普通方程和C2的直角坐标方程;
(2)若C1与C2相交于A,B两点,设P-1,3,求PA?PB.
7.在平面直角坐标系xOy中,直线l的参数方程为,(t为参数,0≤α<π),以原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为,直线l与曲线C的交点为A,B.
(1)若,求AB;
(2)设点P1,1,求的最小值.
8.以直角坐标系的原点为极点,x轴正半轴为极轴建立极坐标系.已知曲线,
M是C1上的动点,点N在射线OM上且满足2ON=OM,设点N的轨迹为C2.
(1)写出曲线C2的极坐标方程,并化为直角坐标方程;
(2)已知直线l的参数方程为 (t为参数,),曲线C2截直线l所得线段的中点
坐标为,求的值.
9.以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,已知在极坐标系中曲线C是以点为圆心,以1为半径的圆,以极点为坐标系原点O,极轴为x轴的非负半轴,且单位长度相同建立平面直角坐标系,直线l的参数方程为(t为参数).
(1)写出l的普通方程及曲线C的极坐标方程;
(2)判断l与C是否相交,若相交,设交点为P,Q两点,求线段PQ的长,若不相交,说明理由.
高频易错题
高频易错题
一、解答题.
1.在平面直角坐标系xOy中,直线l的参数方程为 (t为参数,0≤α<π).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=4cosθ.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设直线l与曲线C交于A?B两点,求△OAB面积的最大值.
精准预测题
精准预测题
一、解答题.
1.在平面直角坐标系xOy中,直线.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求曲线C的直角坐标方程;
(2)若l与C相交于A,B两点,且,求α.
2.已知圆C的参数方程为(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)写出点C的极坐标及圆C的极坐标方程;
(2)点AB分别是圆C和直线l上的点,且,求线段AB长的最小值.
3.在平面直角坐标系中,曲线C的参数方程为(α为参数),以坐标原点O为极点,
x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)设点P0,2,若直线l与曲线C相交于A,B两点,求PA-PB的值.
4.已知在平面直角坐标系xOy中,曲线C1的参数方程为为参数).以原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为.
(1)求曲线C1的普通方程以及曲线C2的直角坐标方程;
(2)若曲线C1、C2交于M、N两点,,求的值.
5.中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其它民俗活动的民间艺术,蕴含了极致的数学美和丰富的文化信息,现有一幅剪纸的设计图(如图),其中的4个小圆均过边长为2的正方形的中心O,且内切于正方形的邻边,现以O为极点,OA为极轴建立极坐标系.
(1)求圆的极坐标方程;
(2)若射线和与图中阴影部分边界有交点,连接所有交点的线段围成了几何图形Ω,求该几何图形Ω的面积.
6.在平面直角坐标系xOy中,曲线C的参数方程为(为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在曲线C上取两点M,N与原点O构成ΔMON,且满足,求ΔMON面积的最大值.
参考答案
参考答案
经典训练题
经典训练题
一、选择题.
1.【答案】A
【解析】由于等边△ABC的两个顶点、,
则线段AB的中点为极点O,
由等腰三角形三线合一的性质可得OC⊥AB,且,
,,因此,顶点C的极坐标可能是,
故选A.
【点评】本题考查顶点的极坐标的求法,考查对称、中点坐标公式等基础知识,考查推理论证能力,考查函数与方程思想,是基础题.
二、解答题.
2.【答案】(1)C:x2+y-12=1,l:x+3y-23=0;(2)1.
【解析】(1)由,可得,
所以曲线C的普通方程为x2+y-12=1,
由,所以,
所以直线l的直角坐标方程为x+3y-23=0.
(2)曲线C的方程可化为x2+y2-2y=0,所以曲线C的极坐标方程为ρ=2sinθ,
由题意设,
将代入ρ=2sinθ,ρ1=1;
将代入,可得ρ2=2,
所以AB=ρ1-ρ2=1.
【点评】本题考查弦长公式,一般求弦长的方法包含以下几点:
1.直角坐标系下的弦长公式AB=1+k2x1+x22-4x1x2或;
2.利用直线参数方程t的几何意义可知AB=t1-t2;
3.极坐标系下,过原点的直线与曲线相交的弦长AB=ρ1-ρ2.
3.【答案】(1)l的参数方程为 (t为参数),C的直角坐标方程为x2=2y;(2)斜率为±2.
【解析】(1)因为直线l过点P(0,2),倾斜角为,
所以直线l的参数方程为 (t为参数);
因为,所以,
所以曲线C的直角坐标方程为x2=2y.
(2)将直线l的参数方程为 (t为参数)代入x2=2y,
可得,
设A,B所对应的参数为t1,t2,所以,,
因为|PA|,|PM|,|PB|成等比数列,
所以,即,
解得,,
故直线l的斜率为±2.
【点评】解题的关键是熟练掌握极坐标与普通方程、参数方程与普通方程的互化;在利用t的几何意义时,要将直线参数方程的标准形式代入到曲线的直角坐标方程里,方可进行求解,考查计算化简的能力,属基础题.
4.【答案】(1);C2:x+y-2=0;(2)22,.
【解析】(1)对于曲线C1有,所以C1的普通方程为.
对于曲线C2有,,
,即C2的直角坐标方程为x+y-2=0.
(2)联立,整理可得4x2-12x+9=0,
Δ=-122-4×4×9=0,所以椭圆C1与直线C2无公共点,
设,
点P到直线x+y-2=0的距离为,
当时,d取最大值为22,
此时点P的坐标为.
【点评】本题主要考查极坐标和参数方程的运算,以及点到直线距离公式的使用,属于中档题.
5.【答案】(1)l:x-y-2=0,x2-y2=8;(2).
【解析】(1)曲线C的参数方程为 (m为参数),
两式平方相减得曲线C的普通方程为x2-y2=8.
直线l的极坐标方程为,则,
转换为直角坐标方程为x-y-2=0.
(2)由,得,所以点P的直角坐标为(3,1),
设圆心为,则a2=(a-3)2+1,解得,
所以,圆的直角坐标方程为.
【点评】(1)关键点:极坐标方程与普通方程的转换主要应用于ρcosθ=x,ρsinθ=y.
(2)求直线与曲线的交点坐标,列方程组、解方程组、可得交点坐标;
求圆的方程可根据圆心x0,y0和半径r,得出圆的方程.
6.【答案】(1),;(2).
【解析】(1)由,得,
由,得,
将x=ρcosθ,y=ρsinθ代入可得x+3y-2=0.
(2)经检验P-1,3在曲线C2上,
则曲线C2的参数方程可写为(t为参数),
代入曲线C1,得13t2+203t+12=0,
设A,B两点对应的参数分别为t1,t2,则由韦达定理得,
故.
【点评】本题解题的关键是理解直线参数方程中t的几何意义.
7.【答案】(1)3;(2).
【解析】(1)由曲线C的极坐标方程得3ρ2+ρ2sin 2θ=12,
化为直角坐标方程为3x2+y2+y2=12,即3x2+4y2=12.
将直线l的参数方程代入其中,得.
当时,上述方程即4t2+8t-5=0,解得,,
所以AB=t1-t2=3.
(2)由根与系数的关系可知:,,
所以,
其中,当时取等号,
所以的最小值为.
【点评】直线参数方程的几何意义:
(1)直线参数方程中参数t的几何意义是这样的:如果点A在定点P的上方,则点A对应的参数tA就表示点A到点P的距离|PA|,即tA=|PA|.
如果点B在定点P的下方,则点B对应的参数tB就表示点B到点P的距离的相反数,
即tB=-|PB|.
(2)由直线参数方程中参数的几何意义得:如果求直线上A,B两点间的距离|AB|,不管A,B两点在哪里,总有|AB|=|tA-tB|.
8.【答案】(1)ρ2=ρ(sinθ+3cosθ),;(2).
【解析】(1)设N(ρ,θ),因为2ON=OM,可得M(2ρ,θ),
代入满足C1的方程,可得,
即,两边同乘以ρ并展开整理得ρ2=ρ(sinθ+3cosθ),
又由,,
所以C2的直角坐标方程为.
(2)将l的参数方程代入C2的直角坐标方程,整理得,
可得,
又由直线l的参数方程经过点,可得t1+t2=0,
即,即tanφ=-3,
因为,所以.
【点评】本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,一元二次方程根与系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题.
9.【答案】(1)l的普通方程为y=x+1,曲线C的极坐标方程为;(2)相交,长度为2.
【解析】(1)l的普通方程为y=x+1,
由,,
曲线C圆心的直角坐标为,
曲线C的直角坐标方程为,
由x=ρcosθ,y=ρsinθ,得,
所以曲线C的极坐标方程.
(2)曲线C圆心的直角坐标为,半径r=1,
所以圆心到直线y=x+1的距离为,
所以l与C是相交,PQ=2r2-d2=2.
【点评】本题考查了极坐标方程,参数方程与普通方程的转化,参数的几何意义,属于中档题.
高频易错题
高频易错题
一、解答题.
1.【答案】(1)l的普通方程为,曲线C的直角坐标方程为(x-2)2+y2=4;(2)最大值是22.
【解析】(1)将直线l的参数方程 (t为参数,0≤α<π)中的参数消去,
得到直线l的普通方程,为,
由曲线C的极坐标方程,可得,
又ρ2=x2+y2,x=ρ?cosθ,∴曲线C的直角坐标方程为,
即(x-2)2+y2=4.
(2)把直线l的参数方程代入到曲线C的直角坐标方程(x-2)2+y2=4,
得,
设A?B对应的参数分别为t1?t2,则,t1?t2=-2,
由参数t的几何意义知:
,
又点O到直线l的距离,
∴△OAB的面积:
,
当,即时等号成立,故△OAB的面积的最大值是22.
【点评】本题考查参数方程和普通方程的转化、极坐标方程和直角坐标方程的转化,关键是能够根据参数t的几何意义将已知弦长用韦达定理的形式表示,再利用点O到直线l的距离表示三角形的高.
精准预测题
精准预测题
一、解答题.
1.【答案】(1)y2=4x;(2).
【解析】(1)由,得.
又∵x=ρcosθ,y=ρsinθ,
的直角坐标方程为y2=4x.
(2)直线l的参数方程为(其中t为参数,),
将它代入y2=4x,得,
设A,B对应的参数分别为t1,t2,则,,
,
又,,,
即.
【点评】直角坐标方程与极坐标方程互化的关键是利用公式,求直线与圆锥曲线的弦长时,
利用直线参数方程的几何意义更简单.
2.【答案】(1)(1,0),ρ2-2ρcosθ-8=0;(2).
【解析】(1)由参数方程知:,
由知:圆C的方程为(x-1)2+y2=9,
∴点C的极坐标是(1,0),
又x=ρcosθ,y=ρsinθ,
∴圆C的极坐标方程为ρ2-2ρcosθ-8=0.
(2)在△ABC中,,
由题意知:直线l为y=x,点C到直线l的距离,
∴,故当时,线段AB的长取得最小值.
【点评】由参数方程结合同角三角函数的平方关系可得普通方程,应用x=ρcosθ,y=ρsinθ将方程转化为极坐标方程;由余弦定理得到|AB|关于|BC|的函数,根据点线距离求得|BC|的范围,应用函数性质即可求|AB|的最小值.
3.【答案】(1)C:x-12+y-22=2,l:x-y+2=0;(2)2.
【解析】(1)由曲线C的参数方程,
得.
∵,
∴曲线C的普通方程为x-12+y-22=2.
由,得ρsinθ-ρcosθ=2.
∵ρcosθ=x,ρsinθ=y,
∴直线l的直角坐标方程为x-y+2=0.
(2)设直线l的参数方程为(t为参数,),设在直线l的参数方程中点A,B所对应的参数分别为t1,t2,
将直线l的参数方程代入曲线C的普通方程,整理得t2-2t-1=0,Δ>0,
则有t1+t2=2,t1t2=-1.
∴PA-PB=t1-t2=t1+t2=2.
【点评】本题考查参数方程、极坐标方程与普通方程的互化,考查与弦长有关问题的求解.
(1)将参数方程化为普通方程式,只需要将原式合理变形,进行消参即可;将极坐标方程化为直角坐标方程为利用求解;
(2)过点Mx0,y0,倾斜角为α的直线l的参数方程为 (t为参数),且t的几何意义为:t是直线上任一点px,y到Mx0,y0的距离,设A,B是直线l上任意两点,则有MA+MB=t1+t2,MA-MB=t1-t2,MA?MB=t1?t2.
4.【答案】(1)曲线C1的普通方程为,曲线C2的直角坐标方程为x-3y-6=0;(2).
【解析】(1)曲线C1的参数方程为为参数),
转换为,
所以①,②,
②-①得.
曲线C2的极坐标方程为,
根据,转换为直角坐标方程为x-3y-6=0.
(2)点在直线x-3y-6=0上,
转换为参数方程为为参数),
代入,得到t2+82t+24=0(t1和t2为点M和N对应的参数),
所以t1+t2=-82,t1t2=24,
所以.
【点评】本题考查极坐标方程与直角坐标方程的互化,参数方程与普通方程的互化,
(1)公式可实现极坐标方程与直角坐标方程的互化;
(2)直线的标准参数方程中参数具有几何意义:过P0x0,y0的直线l的参数方程为(t为参数),则t=P0P.从P0向上的点对应t>0,向下的点对应参数.
5.【答案】(1)ρ=22-2sinθ;(2)3-22.
【解析】(1)依题意,AB=2,所以OB=2,
设圆O1的半径为r,则,即2r=2-2r,解得,
所以圆O1的直角坐标方程为x2+y-2+22=2-22,即x2+y2-22-2y=0,又,所以ρ2-22-2ρsinθ=0,所以ρ=22-2sinθ.
(2)圆O2的直角坐标方程为x+2-22+y2=2-22,
则圆O2的极坐方程为ρ=-22-2cosθ,
当时,;
当时,,
所以Ω的面积.
【点评】本题考查直角坐标方程与极坐标方程的转化,以及极坐标下两点的距离公式的应用,属于中档题.
6.【答案】(1);(2)4.
【解析】(1)可知曲线C的普通方程为x-32+y-12=4,
所以曲线C的极坐标方程为ρ2-23ρcosθ-2ρsinθ=0,
即.
(2)由(1)不妨设Mρ1,θ,,(ρ1>0,ρ2>0),
,
所以ΔMON面积的最大值为4.
【点评】本小题主要考查参数方程、直角坐标方程和和极坐标方程相互转化,考查利用极坐标求解三角形面积的最大值问题.属于中档题.
38177376752专题 11
××
坐标系与参数方程
00专题 11
××
坐标系与参数方程
命题趋势
命题趋势
本部分内容主要考查极坐标方程与普通方程的互化,参数方程与普通方程的互化;已知直线或曲线的参数方程或极坐标方程,求距离、面积等综合问题,本部分考查难度一般不大.
考点清单
考点清单
1.平面直角坐标系中的伸缩变换
设点P(x,y)是平面直角坐标系中的任意一点,在变换的作用下,
点P(x,y)对应到点P'(x',y'),称为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.
2.极坐标系的概念
在平面内取一个定点O,叫做极点;自极点O引一条射线Ox叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.
点M的极坐标:设M是平面内一点,极点O与点M的距离|OM|叫做点M的极径,记为ρ;
以极轴Ox为始边,射线OM为终边的∠xOM叫做点M的极角,记为θ.
有序数对(ρ,θ)叫做点M的极坐标,记为M(ρ,θ).
一般地,不做特殊说明时,我们认为ρ≥0,θ可取任何实数.
注:极坐标(ρ,θ)与(ρ,θ+2kπ)(k∈Z)表示同一个点.极点O的坐标为(0,θ)(θ∈R).
若ρ<0,则-ρ>0,规定点(-ρ,θ)与点(ρ,θ)关于极点对称,即(-ρ,θ)与(ρ,π+θ)表示同一点.
如果规定ρ>0,0≤θ<2π,那么除极点外,平面内的点可用唯一的极坐标(ρ,θ)表示(即一一对应的关系);同时,极坐标(ρ,θ)表示的点也是唯一确定的.
极坐标与直角坐标都是一对有序实数确定平面上一个点,在极坐标系下,一对有序实数ρ、θ对应唯一点P (ρ,θ),但平面内任一个点P的极坐标不唯一.一个点可以有无数个坐标,这些坐标又有规律可循的,P (ρ,θ)(极点除外)的全部坐标为(ρ,θ+2kπ)或(-ρ,θ+(2k+1)π),(k∈Z).极点的极径为0,而极角任意取.若对ρ、θ的取值范围加以限制.
则除极点外,平面上点的极坐标就唯一了,如限定ρ>0,0≤θ<2π或ρ<0,-π<θ≤π等.
极坐标与直角坐标的不同是,直角坐标系中,点与坐标是一一对应的,而极坐标系中,点与坐标是一多对应的.
即一个点的极坐标是不唯一的.
3.极坐标与直角坐标的互化
设M是平面内任意一点,它的直角坐标是(x,y),极坐标是(ρ,θ),从图中可以得出:
,,,.
4.常见曲线的极坐标方程
曲线
图形
极坐标方程
过极点,倾斜角为α的直线
(1)θ=αρ∈R和θ=π+αρ∈R
(2)θ=α(ρ≥0)和θ=π+α(ρ≥0)
过点a?,?0,与极轴垂直的直线
ρcosθ=a
过点,与极轴平行的直线
ρsinθ=a0<θ<π
过点a?,?0,倾斜角为α的直线
ρsinα-θ=asinα
圆心为极点,半径为a的圆
ρ=a0≤θ<2π
圆心为a?,?0,半径为a的圆
圆心为,半径为a的圆
ρ=2asinθ0≤θ<π
5.参数方程的概念
在平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某个变数t的函数,并且对于t的每一个允许值,由这个方程所确定的点M(x,y)都在这条曲线上,那么这个方程就叫做这条曲线的参数方程,联系变数x,y的变数t叫做参变数,简称参数.相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.
6.常见曲线的参数方程
(1)经过定点P(x0,y0),倾斜角为的直线的参数方程(t为参数).
设P是直线上的任意一点,则t表示有向线段P0P的数量.参数的几何意义是有向线段P0P的数量.
(2)圆(x-a)2+(y-b)2=r2的参数方程为(θ为参数);
(3)椭圆的参数方程为(φ为参数);
椭圆的参数方程为(φ为参数);
(4)抛物线y2=2px参数方程为参数,);
参数t的几何意义:抛物线上除顶点外的任意一点与原点连线的斜率的倒数.
7.参数方程与普通方程之间的互化
在建立曲线的参数方程时,要注明参数及参数的取值范围.在参数方程与普通方程的互化中,
必须使x,y的取值范围保持一致.
参数方程化为普通方程的关键是消参数,并且要保证等价性.若不可避免地破坏了同解变形,
则一定要通过.根据t的取值范围导出x,y的取值范围.
精题集训
(70分钟)
精题集训
(70分钟)
经典训练题
经典训练题
一、选择题.
1.极坐标系中,若等边△ABC的两个顶点、,那么顶点C的极坐标可能是( )
A. B. C. D.
二、解答题.
2.在平面直角坐标系中,曲线C的参数方程为(θ为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)射线OP的极坐标方程为,若射线OP与曲线C的交点为A (异于点O),与直线l的交点为B,求线段AB的长.
3.在直角坐标系xOy中,直线l过点P(0,2),倾斜角为.以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos 2θ-2sinθ=0.
(1)求直线l的参数方程与曲线C的直角坐标方程;
(2)若直线l交曲线C于A,B两点,M为AB中点,且满足|PA|,|PM|,|PB|成等比数列,求直线l的斜率.
4.在直角坐标系xOy中,曲线C1的参数方程为 (α为参数).以原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)设P为曲线C1上的动点,求点P到C2的距离的最大值,并求此时点P的坐标.
5.在平面直角坐标系xOy中,曲线C的参数方程为 (m为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)若直线l与曲线C相交于点P,求圆心在极轴上,且经过极点和点P的圆的直角坐标方程.
6.在平面直角坐标系xOy中,曲线C1的参数方程为(θ为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为.
(1)求C1的普通方程和C2的直角坐标方程;
(2)若C1与C2相交于A,B两点,设P-1,3,求PA?PB.
7.在平面直角坐标系xOy中,直线l的参数方程为,(t为参数,0≤α<π),以原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为,直线l与曲线C的交点为A,B.
(1)若,求AB;
(2)设点P1,1,求的最小值.
8.以直角坐标系的原点为极点,x轴正半轴为极轴建立极坐标系.已知曲线,
M是C1上的动点,点N在射线OM上且满足2ON=OM,设点N的轨迹为C2.
(1)写出曲线C2的极坐标方程,并化为直角坐标方程;
(2)已知直线l的参数方程为 (t为参数,),曲线C2截直线l所得线段的中点
坐标为,求的值.
9.以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,已知在极坐标系中曲线C是以点为圆心,以1为半径的圆,以极点为坐标系原点O,极轴为x轴的非负半轴,且单位长度相同建立平面直角坐标系,直线l的参数方程为(t为参数).
(1)写出l的普通方程及曲线C的极坐标方程;
(2)判断l与C是否相交,若相交,设交点为P,Q两点,求线段PQ的长,若不相交,说明理由.
高频易错题
高频易错题
一、解答题.
1.在平面直角坐标系xOy中,直线l的参数方程为 (t为参数,0≤α<π).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=4cosθ.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设直线l与曲线C交于A?B两点,求△OAB面积的最大值.
精准预测题
精准预测题
一、解答题.
1.在平面直角坐标系xOy中,直线.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求曲线C的直角坐标方程;
(2)若l与C相交于A,B两点,且,求α.
2.已知圆C的参数方程为(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)写出点C的极坐标及圆C的极坐标方程;
(2)点AB分别是圆C和直线l上的点,且,求线段AB长的最小值.
3.在平面直角坐标系中,曲线C的参数方程为(α为参数),以坐标原点O为极点,
x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)设点P0,2,若直线l与曲线C相交于A,B两点,求PA-PB的值.
4.已知在平面直角坐标系xOy中,曲线C1的参数方程为为参数).以原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为.
(1)求曲线C1的普通方程以及曲线C2的直角坐标方程;
(2)若曲线C1、C2交于M、N两点,,求的值.
5.中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其它民俗活动的民间艺术,蕴含了极致的数学美和丰富的文化信息,现有一幅剪纸的设计图(如图),其中的4个小圆均过边长为2的正方形的中心O,且内切于正方形的邻边,现以O为极点,OA为极轴建立极坐标系.
(1)求圆的极坐标方程;
(2)若射线和与图中阴影部分边界有交点,连接所有交点的线段围成了几何图形Ω,求该几何图形Ω的面积.
6.在平面直角坐标系xOy中,曲线C的参数方程为(为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在曲线C上取两点M,N与原点O构成ΔMON,且满足,求ΔMON面积的最大值.
参考答案
参考答案
经典训练题
经典训练题
一、选择题.
1.【答案】A
【解析】由于等边△ABC的两个顶点、,
则线段AB的中点为极点O,
由等腰三角形三线合一的性质可得OC⊥AB,且,
,,因此,顶点C的极坐标可能是,
故选A.
【点评】本题考查顶点的极坐标的求法,考查对称、中点坐标公式等基础知识,考查推理论证能力,考查函数与方程思想,是基础题.
二、解答题.
2.【答案】(1)C:x2+y-12=1,l:x+3y-23=0;(2)1.
【解析】(1)由,可得,
所以曲线C的普通方程为x2+y-12=1,
由,所以,
所以直线l的直角坐标方程为x+3y-23=0.
(2)曲线C的方程可化为x2+y2-2y=0,所以曲线C的极坐标方程为ρ=2sinθ,
由题意设,
将代入ρ=2sinθ,ρ1=1;
将代入,可得ρ2=2,
所以AB=ρ1-ρ2=1.
【点评】本题考查弦长公式,一般求弦长的方法包含以下几点:
1.直角坐标系下的弦长公式AB=1+k2x1+x22-4x1x2或;
2.利用直线参数方程t的几何意义可知AB=t1-t2;
3.极坐标系下,过原点的直线与曲线相交的弦长AB=ρ1-ρ2.
3.【答案】(1)l的参数方程为 (t为参数),C的直角坐标方程为x2=2y;(2)斜率为±2.
【解析】(1)因为直线l过点P(0,2),倾斜角为,
所以直线l的参数方程为 (t为参数);
因为,所以,
所以曲线C的直角坐标方程为x2=2y.
(2)将直线l的参数方程为 (t为参数)代入x2=2y,
可得,
设A,B所对应的参数为t1,t2,所以,,
因为|PA|,|PM|,|PB|成等比数列,
所以,即,
解得,,
故直线l的斜率为±2.
【点评】解题的关键是熟练掌握极坐标与普通方程、参数方程与普通方程的互化;在利用t的几何意义时,要将直线参数方程的标准形式代入到曲线的直角坐标方程里,方可进行求解,考查计算化简的能力,属基础题.
4.【答案】(1);C2:x+y-2=0;(2)22,.
【解析】(1)对于曲线C1有,所以C1的普通方程为.
对于曲线C2有,,
,即C2的直角坐标方程为x+y-2=0.
(2)联立,整理可得4x2-12x+9=0,
Δ=-122-4×4×9=0,所以椭圆C1与直线C2无公共点,
设,
点P到直线x+y-2=0的距离为,
当时,d取最大值为22,
此时点P的坐标为.
【点评】本题主要考查极坐标和参数方程的运算,以及点到直线距离公式的使用,属于中档题.
5.【答案】(1)l:x-y-2=0,x2-y2=8;(2).
【解析】(1)曲线C的参数方程为 (m为参数),
两式平方相减得曲线C的普通方程为x2-y2=8.
直线l的极坐标方程为,则,
转换为直角坐标方程为x-y-2=0.
(2)由,得,所以点P的直角坐标为(3,1),
设圆心为,则a2=(a-3)2+1,解得,
所以,圆的直角坐标方程为.
【点评】(1)关键点:极坐标方程与普通方程的转换主要应用于ρcosθ=x,ρsinθ=y.
(2)求直线与曲线的交点坐标,列方程组、解方程组、可得交点坐标;
求圆的方程可根据圆心x0,y0和半径r,得出圆的方程.
6.【答案】(1),;(2).
【解析】(1)由,得,
由,得,
将x=ρcosθ,y=ρsinθ代入可得x+3y-2=0.
(2)经检验P-1,3在曲线C2上,
则曲线C2的参数方程可写为(t为参数),
代入曲线C1,得13t2+203t+12=0,
设A,B两点对应的参数分别为t1,t2,则由韦达定理得,
故.
【点评】本题解题的关键是理解直线参数方程中t的几何意义.
7.【答案】(1)3;(2).
【解析】(1)由曲线C的极坐标方程得3ρ2+ρ2sin 2θ=12,
化为直角坐标方程为3x2+y2+y2=12,即3x2+4y2=12.
将直线l的参数方程代入其中,得.
当时,上述方程即4t2+8t-5=0,解得,,
所以AB=t1-t2=3.
(2)由根与系数的关系可知:,,
所以,
其中,当时取等号,
所以的最小值为.
【点评】直线参数方程的几何意义:
(1)直线参数方程中参数t的几何意义是这样的:如果点A在定点P的上方,则点A对应的参数tA就表示点A到点P的距离|PA|,即tA=|PA|.
如果点B在定点P的下方,则点B对应的参数tB就表示点B到点P的距离的相反数,
即tB=-|PB|.
(2)由直线参数方程中参数的几何意义得:如果求直线上A,B两点间的距离|AB|,不管A,B两点在哪里,总有|AB|=|tA-tB|.
8.【答案】(1)ρ2=ρ(sinθ+3cosθ),;(2).
【解析】(1)设N(ρ,θ),因为2ON=OM,可得M(2ρ,θ),
代入满足C1的方程,可得,
即,两边同乘以ρ并展开整理得ρ2=ρ(sinθ+3cosθ),
又由,,
所以C2的直角坐标方程为.
(2)将l的参数方程代入C2的直角坐标方程,整理得,
可得,
又由直线l的参数方程经过点,可得t1+t2=0,
即,即tanφ=-3,
因为,所以.
【点评】本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,一元二次方程根与系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题.
9.【答案】(1)l的普通方程为y=x+1,曲线C的极坐标方程为;(2)相交,长度为2.
【解析】(1)l的普通方程为y=x+1,
由,,
曲线C圆心的直角坐标为,
曲线C的直角坐标方程为,
由x=ρcosθ,y=ρsinθ,得,
所以曲线C的极坐标方程.
(2)曲线C圆心的直角坐标为,半径r=1,
所以圆心到直线y=x+1的距离为,
所以l与C是相交,PQ=2r2-d2=2.
【点评】本题考查了极坐标方程,参数方程与普通方程的转化,参数的几何意义,属于中档题.
高频易错题
高频易错题
一、解答题.
1.【答案】(1)l的普通方程为,曲线C的直角坐标方程为(x-2)2+y2=4;(2)最大值是22.
【解析】(1)将直线l的参数方程 (t为参数,0≤α<π)中的参数消去,
得到直线l的普通方程,为,
由曲线C的极坐标方程,可得,
又ρ2=x2+y2,x=ρ?cosθ,∴曲线C的直角坐标方程为,
即(x-2)2+y2=4.
(2)把直线l的参数方程代入到曲线C的直角坐标方程(x-2)2+y2=4,
得,
设A?B对应的参数分别为t1?t2,则,t1?t2=-2,
由参数t的几何意义知:
,
又点O到直线l的距离,
∴△OAB的面积:
,
当,即时等号成立,故△OAB的面积的最大值是22.
【点评】本题考查参数方程和普通方程的转化、极坐标方程和直角坐标方程的转化,关键是能够根据参数t的几何意义将已知弦长用韦达定理的形式表示,再利用点O到直线l的距离表示三角形的高.
精准预测题
精准预测题
一、解答题.
1.【答案】(1)y2=4x;(2).
【解析】(1)由,得.
又∵x=ρcosθ,y=ρsinθ,
的直角坐标方程为y2=4x.
(2)直线l的参数方程为(其中t为参数,),
将它代入y2=4x,得,
设A,B对应的参数分别为t1,t2,则,,
,
又,,,
即.
【点评】直角坐标方程与极坐标方程互化的关键是利用公式,求直线与圆锥曲线的弦长时,
利用直线参数方程的几何意义更简单.
2.【答案】(1)(1,0),ρ2-2ρcosθ-8=0;(2).
【解析】(1)由参数方程知:,
由知:圆C的方程为(x-1)2+y2=9,
∴点C的极坐标是(1,0),
又x=ρcosθ,y=ρsinθ,
∴圆C的极坐标方程为ρ2-2ρcosθ-8=0.
(2)在△ABC中,,
由题意知:直线l为y=x,点C到直线l的距离,
∴,故当时,线段AB的长取得最小值.
【点评】由参数方程结合同角三角函数的平方关系可得普通方程,应用x=ρcosθ,y=ρsinθ将方程转化为极坐标方程;由余弦定理得到|AB|关于|BC|的函数,根据点线距离求得|BC|的范围,应用函数性质即可求|AB|的最小值.
3.【答案】(1)C:x-12+y-22=2,l:x-y+2=0;(2)2.
【解析】(1)由曲线C的参数方程,
得.
∵,
∴曲线C的普通方程为x-12+y-22=2.
由,得ρsinθ-ρcosθ=2.
∵ρcosθ=x,ρsinθ=y,
∴直线l的直角坐标方程为x-y+2=0.
(2)设直线l的参数方程为(t为参数,),设在直线l的参数方程中点A,B所对应的参数分别为t1,t2,
将直线l的参数方程代入曲线C的普通方程,整理得t2-2t-1=0,Δ>0,
则有t1+t2=2,t1t2=-1.
∴PA-PB=t1-t2=t1+t2=2.
【点评】本题考查参数方程、极坐标方程与普通方程的互化,考查与弦长有关问题的求解.
(1)将参数方程化为普通方程式,只需要将原式合理变形,进行消参即可;将极坐标方程化为直角坐标方程为利用求解;
(2)过点Mx0,y0,倾斜角为α的直线l的参数方程为 (t为参数),且t的几何意义为:t是直线上任一点px,y到Mx0,y0的距离,设A,B是直线l上任意两点,则有MA+MB=t1+t2,MA-MB=t1-t2,MA?MB=t1?t2.
4.【答案】(1)曲线C1的普通方程为,曲线C2的直角坐标方程为x-3y-6=0;(2).
【解析】(1)曲线C1的参数方程为为参数),
转换为,
所以①,②,
②-①得.
曲线C2的极坐标方程为,
根据,转换为直角坐标方程为x-3y-6=0.
(2)点在直线x-3y-6=0上,
转换为参数方程为为参数),
代入,得到t2+82t+24=0(t1和t2为点M和N对应的参数),
所以t1+t2=-82,t1t2=24,
所以.
【点评】本题考查极坐标方程与直角坐标方程的互化,参数方程与普通方程的互化,
(1)公式可实现极坐标方程与直角坐标方程的互化;
(2)直线的标准参数方程中参数具有几何意义:过P0x0,y0的直线l的参数方程为(t为参数),则t=P0P.从P0向上的点对应t>0,向下的点对应参数.
5.【答案】(1)ρ=22-2sinθ;(2)3-22.
【解析】(1)依题意,AB=2,所以OB=2,
设圆O1的半径为r,则,即2r=2-2r,解得,
所以圆O1的直角坐标方程为x2+y-2+22=2-22,即x2+y2-22-2y=0,又,所以ρ2-22-2ρsinθ=0,所以ρ=22-2sinθ.
(2)圆O2的直角坐标方程为x+2-22+y2=2-22,
则圆O2的极坐方程为ρ=-22-2cosθ,
当时,;
当时,,
所以Ω的面积.
【点评】本题考查直角坐标方程与极坐标方程的转化,以及极坐标下两点的距离公式的应用,属于中档题.
6.【答案】(1);(2)4.
【解析】(1)可知曲线C的普通方程为x-32+y-12=4,
所以曲线C的极坐标方程为ρ2-23ρcosθ-2ρsinθ=0,
即.
(2)由(1)不妨设Mρ1,θ,,(ρ1>0,ρ2>0),
,
所以ΔMON面积的最大值为4.
【点评】本小题主要考查参数方程、直角坐标方程和和极坐标方程相互转化,考查利用极坐标求解三角形面积的最大值问题.属于中档题.
同课章节目录
