2021届高考数学(文)二轮专题五 三角函数与解三角形(文) 学案Word
文档属性
| 名称 | 2021届高考数学(文)二轮专题五 三角函数与解三角形(文) 学案Word |  | |
| 格式 | docx | ||
| 文件大小 | 989.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 21:18:43 | ||
图片预览




文档简介
313690229235
38177376752专题 5
××
三角函数与解三角形
00专题 5
××
三角函数与解三角形
命题趋势
命题趋势
1.三角函数
(1)以正弦函数、余弦函数、正切函数为载体,考查函数的定义域、最值、单调性、对称性、周期性.
(2)考查三角函数式的化简,三角函数的图象的性质以及平移和伸缩变换.
2.解三角形
(1)利用正余弦定理进行三角形边和角的计算,三角形形状的判断、面积的计算,以及有关的参数的范围.
(2)考查运用正余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
考点清单
考点清单
一、三角函数
1.公式
(1)诱导公式:
正弦
余弦
正切
α+k?2π
sinα
cosα
tanα
α+π
-sinα
-cosα
tanα
-α
-sinα
cosα
-tanα
π-α
sinα
-cosα
-tanα
cosα
-sinα
cosα
sinα
-cosα
sinα
-cosα
-sinα
(2)同角三角函数关系式:
,
(3)两角和与差的三角函数:
(4)二倍角公式:
(5)降幂公式:
,
2.三角函数性质
性质
奇偶性
奇函数
偶函数
单调性
在区间上是增函数,
在区间上是减函数
在区间上是增函数,
在区间上是减函数
最值
在时,ymax;
在时,ymin
在x=2kπ(k∈Z)时,ymax;
在x=2kπ+π(k∈Z)时,ymin
对称中心
(kπ,0)(k∈Z)
对称轴
x=kπ(k∈Z)
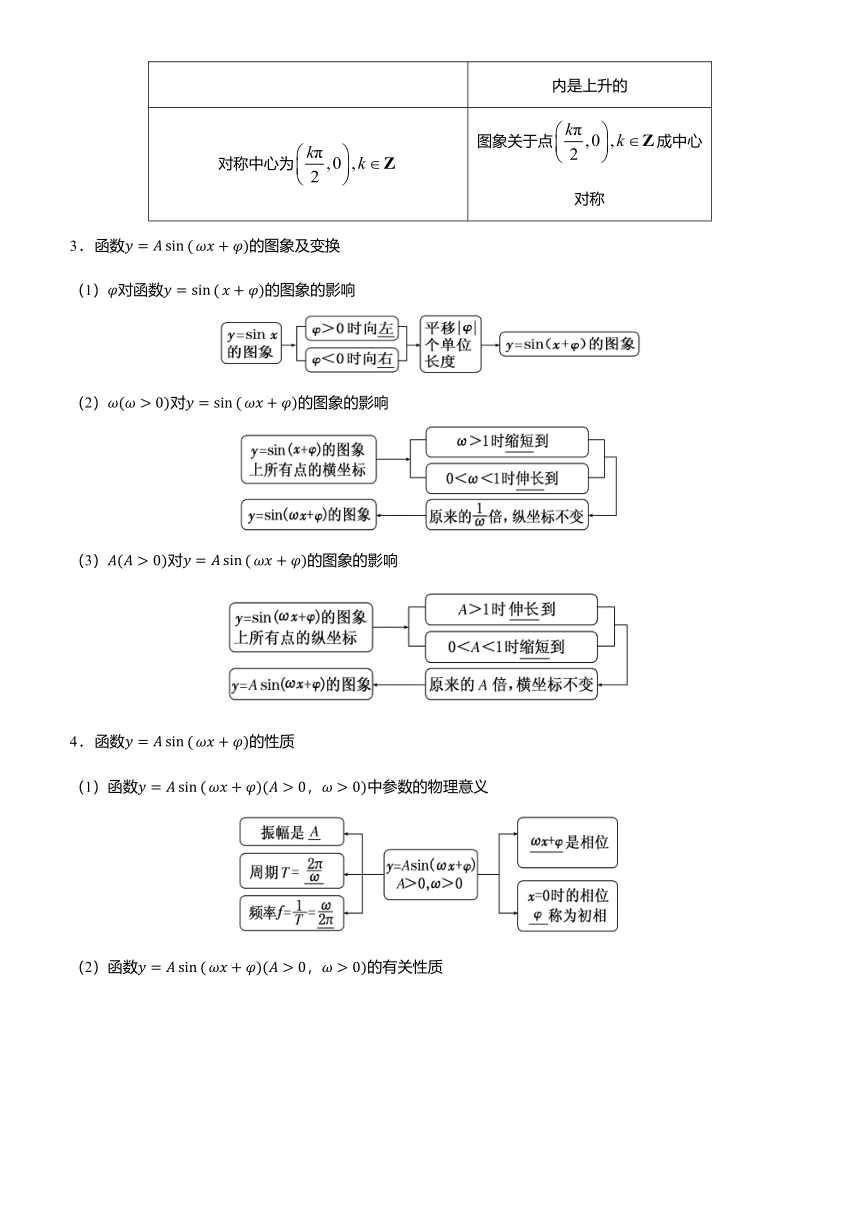
正切函数的性质
图象特点
定义域为
图象与直线没有交点
值域为R
图象向上、向下无限延伸
最小正周期为π
在区间上图象完全一样
在内是增函数
图象在内是上升的
对称中心为
图象关于点成中心对称
3.函数y=Asin(ωx+φ)的图象及变换
(1)φ对函数y=sin(x+φ)的图象的影响
(2)ω(ω>0)对y=sin(ωx+φ)的图象的影响
(3)A(A>0)对y=Asin(ωx+φ)的图象的影响
4.函数y=Asin(ωx+φ)的性质
(1)函数y=Asin(ωx+φ)(A>0,ω>0)中参数的物理意义
(2)函数y=Asin(ωx+φ)(A>0,ω>0)的有关性质
二、解三角形
1.正余弦定理
定理
正弦定理
余弦定理
内容
(为外接圆半径)
;
;
变形形式
,,
;
,,
;
;
;
;
2.利用正弦、余弦定理解三角形
(1)已知两角一边,用正弦定理,只有一解.
(2)已知两边及一边的对角,用正弦定理,有解的情况可分为几种情况.
在中,已知,和角时,解得情况如下:
为锐角
为钝角或直角
直角图形
关系式
解的个数
一解
两解
一解
一解
上表中为锐角时,,无解.
为钝角或直角时,,均无解.
(3)已知三边,用余弦定理,有解时,只有一解.
(4)已知两边及夹角,用余弦定理,必有一解.
3.三角形中常用的面积公式
(1)(表示边上的高);
(2);
(3)(为三角形的内切圆半径).
4.解三角形应用题的一般步骤
精题集训
(70分钟)
精题集训
(70分钟)
经典训练题
经典训练题
一、选择题.
1.若,则( )
A. B. C. D.
2.函数的最大值为( )
A. B. C. D.3
3.已知锐角满足.若要得到函数的图象,则可以将函数的图象( )
A.向左平移个单位长度 B.向左平移个单位长度
C.向右平移个单位长度 D.向右平移个单位长度
4.已知函数fx=2sinωx+φ,的部分图象如图所示,fx的图象过,两点,将fx的图象向左平移个单位得到gx的图象,则函数gx在上的最小值为( )
A.-2 B.2 C.-3 D.-1
5.已知函数fx=sinωx-3cosωx(,)的图象与x轴交点的横坐标构成一个公差为的等差数列,把函数fx的图象沿x轴向左平移个单位,横坐标伸长到原来的2倍得到函数gx的图象,则下列关于函数gx的命题中正确的是( )
A.函数gx是奇函数 B.gx的图象关于直线对称
C.gx在上是增函数 D.当时,函数gx的值域是[0,2]
6.在△ABC中,内角A,B,C所对边分别为a,b,c,若,b=4,△ABC的面积为33,则sinB=( )
A. B. C. D.
7.已知a、b、c分别是△ABC的内角A、B、C的对边,若,则ΔABC的形状为( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
二、填空题.
8.已知,且有1-2sin2α=cos2α,则cosα=_________.
9.已知角α的顶点为坐标原点,始边为x轴的正半轴,终边经过点P3,4,则___________.
三、解答题.
10.已知函数.
(1)求函数f(x)在区间0,π上的值域;
(2)若方程f(ωx)=3(ω>0)在区间0,π上至少有两个不同的解,求ω的取值范围.
11.已知函数.
(1)求函数fx在上的单调区间;
(2)若,,求的值.
12.在四边形ABCD中,AB//CD,AD=CD=BD=1.
(1)若,求BC;
(2)若AB=2BC,求.
13.在△ABC中,角A,B,C所对的边分别为a,b,c,满足2b-ccosA=acosC.
(1)求角A;
(2)若a=13,b+c=5,求△ABC的面积.
14.已知△ABC的内角A,B,C的对边分别为a,b,c,且asinA+B-C=csinB+C.
(1)求角C的大小;
(2)若2a+b=8,且△ABC的面积为23,求△ABC的周长.
15.在△ABC中,内角A,B,C的对边分别为a,b,c.已知2csinB=3asinC,.
(1)求证:△ABC为等腰三角形;
(2)若△ABC面积为22,D为AB中点,求线段CD的长.
16.△ABC的内角A,B,C的对边分别为a,b,c.已知.
(1)求A;
(2)已知b=1,c=3,且边BC上有一点D满足,求AD.
高频易错题
高频易错题
一、选择题.
1.已知函数,现将的图象向左平移个单位,再将所得图象上各点的横坐标缩短为原来的倍,纵坐标不变,得到函数y=gx的图象,则gx的解析式为( )
A. B.
C. D.
二、填空题.
2.设锐角三角形ABC的三个内角A、B、C所对的边分别为a、b、c,若a=2,B=2A,则b的取值范围为___________.
精准预测题
精准预测题
一、选择题.
1.如图,角α,β的顶点与原点O重合,始边与x轴的非负半轴重合,终边与单位圆O分别交于A,B两点,则OA?OB=( )
A.cos(α-β) B.cos(α+β) C.sin(α-β) D.sin(α+β)
2.已知,则( )
A. B.4 C. D.
二、解答题.
3.已知函数.
(1)若,求的值;
(2)若函数f(x)图象上所有点的纵坐标保持不变,横坐标变为原来的倍得函数g(x)的图象,求函数g(x)在得的值域.
4.设函数.
(1)求f(x)的最小正周期和值域;
(2)在锐角△ABC中,角A?B?C的对边长分别为a?b?c.若f(A)=-5,a=3,求△ABC周长的取值范围.
参考答案
参考答案
经典训练题
经典训练题
一、选择题.
1.【答案】A
【解析】,
,故选A.
【点评】本题主要考查了诱导公式在三角函数化简求值中的应用,考查了计算能力和转化思想,
属于基础题.
2.【答案】B
【解析】因为,
所以,
令,则,
则,
令f'θ=0,得或,
当时,f'θ<0;时,f'θ>0,
所以当时,fθ取得最大值,此时,
所以,故选B.
【点评】本题考查三角恒等变换及三角函数的性质的应用,解答的关键是利用导数研究函数的单调性从而求出函数的最值.
3.【答案】A
【解析】由,知,即,
∴锐角,
故,
又,
∴,故f(x)是将向左平移个单位长度得到,故选A.
【点评】由辅助角公式化简已知条件求锐角,根据f(x)的函数式,应用二倍角、诱导公式将f(x)化为正弦型函数,即可判断图象的平移方式.
4.【答案】A
【解析】由图象知,,∴T=2π,则,
∴fx=2sinx+φ,
将点的坐标代入得,,即,
又,∴,则,
将fx的图象向左平移个单位得到函数,
∴gx在上的最小值为,故选A.
【点评】本题主要考查三角函数图象,需要利用三角函数的周期性以及对称性进行处理,再结合图象的平移,三角函数的单调性进行解题,本题属于中档题.
5.【答案】B
【解析】,
由题意知函数周期为π,则,,
从而,
把函数fx的图象沿x轴向左平移个单位,
横坐标伸长到原来的2倍得到函数,
gx不是奇函数,A错;
gx在是单调递增,C错;
时,函数gx的值域是[1,2],D错;
gx的图象关于直线对称,B对,
只有选项B正确,故选B.
【点评】本题考查三角函数,图象的变换,以及图象的性质,属于中档题.
6.【答案】A
【解析】,所以c=3,
由余弦定理可得,得a=13,
又由正弦定理可得,所以,故选A.
【点评】本题主要考了三角形的面积公式以及余弦定理公式的运用,属于基础题型.
7.【答案】A
【解析】因为在三角形中,变形为,
由内角和定理可得,
化简可得,,所以,
所以三角形为钝角三角形,故选A.
【点评】本题考查了解三角形,主要是公式的变形是解题的关键,属于较为基础题.
二、填空题.
8.【答案】
【解析】,
因为,所以,
因此由,
而,把代入(1)得:
,而,
因此,故答案为.
【点评】本题考查了三角恒等变换与三角函数求值问题,是基础题.
9.【答案】
【解析】由三角函数的定义可得,,
因此,,
故答案为.
【点评】本题考查任意角的三角函数的应用,诱导公式的应用,是基本知识的考查.
三、解答题.
10.【答案】(1);(2).
【解析】(1),
令,,,
由y=sinU的图象知,,即,
,所以函数f(x)的值域为.
(2),
∵f(ωx)=3,,即,
∵x∈0,π,,
且或,
由于方程f(ωx)=3(ω>0)在区间0,π上至少有两个不同的解,
所以,解得,
所以ω的取值范围为.
【点评】考查三角函数的值域时,常用的方法:
(1)将函数化简整理为f(x)=Asinωx+φ,再利用三角函数性质求值域;
(2)利用导数研究三角函数的单调区间,从而求出函数的最值.
11.【答案】(1)递增区间为,,递减区间为;(2).
【解析】(1)由题意得
,
因为,所以,
令,解得;
令,解得;
令,得.
所以函数fx在上的单调递增区间为,,
单调递减区间为.
(2)由(1)知.
因为,所以,
又因为,所以,
所以.
【点评】三角函数的化简求值的规律总结:
1.给角求值:一般给出的角是非特殊角,要观察所给角与特殊角的关系,利用三角变换转化为求特殊角的三角函数值问题;
2.给值求值:即给出某些角的三角函数值,求另外一些角的三角函数值,解题关键在于“变角”,使相关角相同或具有某种关系;
3.给值求角:实质上可转化为“给值求值”即通过求角的某个三角函数值来求角(注意角的范围).
12.【答案】(1);(2).
【解析】(1)在△ABD中,由余弦定理可得,
∵CD//AB,∴∠BDC=∠ABD,
在△BCD中,由余弦定理可得,.
(2)设BC=x,则AB=2x,
在△ABD中,,
在△BCD中,,
由(1)可知,∠BDC=∠ABD,所以,cos∠BDC=cos∠ABD,即,
整理可得x2+2x-2=0,
因为x>0,解得x=3-1,
因此,.
【点评】在解三角形的问题中,若已知条件同时含有边和角,但不能直接使用正弦定理或余弦定理得到答案,要选择“边化角”或“角化边”,变换原则如下:
(1)若式子中含有正弦的齐次式,优先考虑正弦定理“角化边”;
(2)若式子中含有a、b、c的齐次式,优先考虑正弦定理“边化角”;
(3)若式子中含有余弦的齐次式,优先考虑余弦定理“角化边”;
(4)代数式变形或者三角恒等变换前置;
(5)含有面积公式的问题,要考虑结合余弦定理求解;
(6)同时出现两个自由角(或三个自由角)时,要用到三角形的内角和定理.
13.【答案】(1);(2)3.
【解析】(1)在三角形ABC中,∵2b-ccosA=acosC,
由正弦定理得,
化为:,
三角形中,解得,A∈0,π,
∴.
(2)由余弦定理得,
∵a=13,b+c=5,
∴13=b+c2-3cb=52-3bc,化为bc=4,
所以三角形ABC的面积.
【点评】本题考查正余弦定理和三角形面积公式的综合运用,涉及三角函数恒等变换,属基础题.熟练掌握利用正弦定理边化角,并结合三角函数两角和差公式化简,注意余弦定理与三角形面积公式的综合运用.
14.【答案】(1);(2)6+23.
【解析】(1)∵asin(A+B-C)=csin(B+C),,
,
,,,.
(2)由题意可得,∴ab=8,
∵2a+b=8联立可得,a=2,b=4,
由余弦定理可得c2=12,c=23,此时周长为6+23.
【点评】本题主要考查了三角形的内角及诱导公式在三角形化简中的应用,还考查了三角形的面积公式及余弦定理,属于基础题.
15.【答案】(1)证明见解析;(2).
【解析】(1)由2csinB=3asinC,
根据正弦定理可得2cb=3ac,所以2b=3a,则,
又,根据余弦定理可得,
则,所以,
因此△ABC为等腰三角形.
(2)因为角C是三角形内角,所以sinC>0,则,
因为△ABC面积为22,
所以,解得a=2,所以b=c=3,
又D为AB中点,所以,
则,整理得,所以.
【点评】本题主要考查正余弦定理、三角形的面积公式的综合运用,利用正弦定理进行边角转换等,
属于中档题型.
16.【答案】(1);(2).
【解析】(1)因为,由正弦定理得,
因为sinC≠0,所以,所以,
因为,所以,
所以,即,所以.
(2)设△ABD的AB边上的高为h1,△ADC的AC边上的高为h2,
因为,c=3,b=1,所以,
所以h1=h2,AD是△ABC角A的内角平分线,所以,
因为S△ABD=3S△ADC,可知,
所以,所以.
【点评】关键点点睛:本题考查了正弦定理的边角互化、三角形的面积公式,解题的关键是确定AD是△ABC角A的内角平分线,考查了运算能力.
高频易错题
高频易错题
一、选择题.
1.【答案】C
【解析】将的图象向左平移个单位得,
再所得图象上各点的横坐标缩短为原来的倍,纵坐标不变,得到,
故选C.
【点评】在三角函数平移变换中,y=sinωx向左平移个单位得到的函数解析式为y=sinωx+φ=sinωx+ωφ,而不是y=sinωx+,考查运算求解能力,是基础题.
二、填空题.
2.【答案】(22,23)
【解析】由,得b=4cosA,由,
,故,
所以,所以b=4cosA∈22,23.
【点评】该题考查的是有关解三角形的问题,涉及到的知识点有正弦定理,以及锐角三角形的条件,属于简单题目.
精准预测题
精准预测题
一、选择题.
1.【答案】A
【解析】由图可知,,
所以,故选A.
【点评】本题考查运用向量进行余弦定理的证明,属于基础题型.
2.【答案】C
【解析】因为,
利用诱导公式可得,即,
所以,故选C.
【点评】本题主要考查诱导公式,正切的两角和差公式的应用,属于基础题.
二、解答题.
3.【答案】(1);(2)-1,2.
【解析】(1),
因为,所以,
即,所以-33sinα=cosα,所以.
(2)f(x)图象上所有点横坐标变为原来的倍得到函数g(x)的图象,
所以g(x)的解析式为,
因为,所以,则,
所以-1≤g(x)≤2,
故g(x)在上的值域为-1,2.
【点评】本题主要考查三角恒等变换,同角三角函数的基本关系,函数y=Asinωx+φ的图象变换规律,正弦函数的定义域和值域,属于中档题.
4.【答案】(1)π,-43+1,43+1(2)(3+3,33].
【解析】(1)
,
,值域为-43+1,43+1.
(2)由f(A)=-5,可得,
因为三角形为锐角△ABC,
所以,即,,
由正弦定理,得,,
所以
.
因为△ABC为锐角三角形,所以,,
即,解得,
所以,,即,
所以周长的取值范围为区间(3+3,33].
【点评】在解三角形的周长范围时,将a+b+c转化为含一个角的三角函数问题,利用三角函数的值域,
求周长的取值范围,是常用解法.
38177376752专题 5
××
三角函数与解三角形
00专题 5
××
三角函数与解三角形
命题趋势
命题趋势
1.三角函数
(1)以正弦函数、余弦函数、正切函数为载体,考查函数的定义域、最值、单调性、对称性、周期性.
(2)考查三角函数式的化简,三角函数的图象的性质以及平移和伸缩变换.
2.解三角形
(1)利用正余弦定理进行三角形边和角的计算,三角形形状的判断、面积的计算,以及有关的参数的范围.
(2)考查运用正余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
考点清单
考点清单
一、三角函数
1.公式
(1)诱导公式:
正弦
余弦
正切
α+k?2π
sinα
cosα
tanα
α+π
-sinα
-cosα
tanα
-α
-sinα
cosα
-tanα
π-α
sinα
-cosα
-tanα
cosα
-sinα
cosα
sinα
-cosα
sinα
-cosα
-sinα
(2)同角三角函数关系式:
,
(3)两角和与差的三角函数:
(4)二倍角公式:
(5)降幂公式:
,
2.三角函数性质
性质
奇偶性
奇函数
偶函数
单调性
在区间上是增函数,
在区间上是减函数
在区间上是增函数,
在区间上是减函数
最值
在时,ymax;
在时,ymin
在x=2kπ(k∈Z)时,ymax;
在x=2kπ+π(k∈Z)时,ymin
对称中心
(kπ,0)(k∈Z)
对称轴
x=kπ(k∈Z)
正切函数的性质
图象特点
定义域为
图象与直线没有交点
值域为R
图象向上、向下无限延伸
最小正周期为π
在区间上图象完全一样
在内是增函数
图象在内是上升的
对称中心为
图象关于点成中心对称
3.函数y=Asin(ωx+φ)的图象及变换
(1)φ对函数y=sin(x+φ)的图象的影响
(2)ω(ω>0)对y=sin(ωx+φ)的图象的影响
(3)A(A>0)对y=Asin(ωx+φ)的图象的影响
4.函数y=Asin(ωx+φ)的性质
(1)函数y=Asin(ωx+φ)(A>0,ω>0)中参数的物理意义
(2)函数y=Asin(ωx+φ)(A>0,ω>0)的有关性质
二、解三角形
1.正余弦定理
定理
正弦定理
余弦定理
内容
(为外接圆半径)
;
;
变形形式
,,
;
,,
;
;
;
;
2.利用正弦、余弦定理解三角形
(1)已知两角一边,用正弦定理,只有一解.
(2)已知两边及一边的对角,用正弦定理,有解的情况可分为几种情况.
在中,已知,和角时,解得情况如下:
为锐角
为钝角或直角
直角图形
关系式
解的个数
一解
两解
一解
一解
上表中为锐角时,,无解.
为钝角或直角时,,均无解.
(3)已知三边,用余弦定理,有解时,只有一解.
(4)已知两边及夹角,用余弦定理,必有一解.
3.三角形中常用的面积公式
(1)(表示边上的高);
(2);
(3)(为三角形的内切圆半径).
4.解三角形应用题的一般步骤
精题集训
(70分钟)
精题集训
(70分钟)
经典训练题
经典训练题
一、选择题.
1.若,则( )
A. B. C. D.
2.函数的最大值为( )
A. B. C. D.3
3.已知锐角满足.若要得到函数的图象,则可以将函数的图象( )
A.向左平移个单位长度 B.向左平移个单位长度
C.向右平移个单位长度 D.向右平移个单位长度
4.已知函数fx=2sinωx+φ,的部分图象如图所示,fx的图象过,两点,将fx的图象向左平移个单位得到gx的图象,则函数gx在上的最小值为( )
A.-2 B.2 C.-3 D.-1
5.已知函数fx=sinωx-3cosωx(,)的图象与x轴交点的横坐标构成一个公差为的等差数列,把函数fx的图象沿x轴向左平移个单位,横坐标伸长到原来的2倍得到函数gx的图象,则下列关于函数gx的命题中正确的是( )
A.函数gx是奇函数 B.gx的图象关于直线对称
C.gx在上是增函数 D.当时,函数gx的值域是[0,2]
6.在△ABC中,内角A,B,C所对边分别为a,b,c,若,b=4,△ABC的面积为33,则sinB=( )
A. B. C. D.
7.已知a、b、c分别是△ABC的内角A、B、C的对边,若,则ΔABC的形状为( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
二、填空题.
8.已知,且有1-2sin2α=cos2α,则cosα=_________.
9.已知角α的顶点为坐标原点,始边为x轴的正半轴,终边经过点P3,4,则___________.
三、解答题.
10.已知函数.
(1)求函数f(x)在区间0,π上的值域;
(2)若方程f(ωx)=3(ω>0)在区间0,π上至少有两个不同的解,求ω的取值范围.
11.已知函数.
(1)求函数fx在上的单调区间;
(2)若,,求的值.
12.在四边形ABCD中,AB//CD,AD=CD=BD=1.
(1)若,求BC;
(2)若AB=2BC,求.
13.在△ABC中,角A,B,C所对的边分别为a,b,c,满足2b-ccosA=acosC.
(1)求角A;
(2)若a=13,b+c=5,求△ABC的面积.
14.已知△ABC的内角A,B,C的对边分别为a,b,c,且asinA+B-C=csinB+C.
(1)求角C的大小;
(2)若2a+b=8,且△ABC的面积为23,求△ABC的周长.
15.在△ABC中,内角A,B,C的对边分别为a,b,c.已知2csinB=3asinC,.
(1)求证:△ABC为等腰三角形;
(2)若△ABC面积为22,D为AB中点,求线段CD的长.
16.△ABC的内角A,B,C的对边分别为a,b,c.已知.
(1)求A;
(2)已知b=1,c=3,且边BC上有一点D满足,求AD.
高频易错题
高频易错题
一、选择题.
1.已知函数,现将的图象向左平移个单位,再将所得图象上各点的横坐标缩短为原来的倍,纵坐标不变,得到函数y=gx的图象,则gx的解析式为( )
A. B.
C. D.
二、填空题.
2.设锐角三角形ABC的三个内角A、B、C所对的边分别为a、b、c,若a=2,B=2A,则b的取值范围为___________.
精准预测题
精准预测题
一、选择题.
1.如图,角α,β的顶点与原点O重合,始边与x轴的非负半轴重合,终边与单位圆O分别交于A,B两点,则OA?OB=( )
A.cos(α-β) B.cos(α+β) C.sin(α-β) D.sin(α+β)
2.已知,则( )
A. B.4 C. D.
二、解答题.
3.已知函数.
(1)若,求的值;
(2)若函数f(x)图象上所有点的纵坐标保持不变,横坐标变为原来的倍得函数g(x)的图象,求函数g(x)在得的值域.
4.设函数.
(1)求f(x)的最小正周期和值域;
(2)在锐角△ABC中,角A?B?C的对边长分别为a?b?c.若f(A)=-5,a=3,求△ABC周长的取值范围.
参考答案
参考答案
经典训练题
经典训练题
一、选择题.
1.【答案】A
【解析】,
,故选A.
【点评】本题主要考查了诱导公式在三角函数化简求值中的应用,考查了计算能力和转化思想,
属于基础题.
2.【答案】B
【解析】因为,
所以,
令,则,
则,
令f'θ=0,得或,
当时,f'θ<0;时,f'θ>0,
所以当时,fθ取得最大值,此时,
所以,故选B.
【点评】本题考查三角恒等变换及三角函数的性质的应用,解答的关键是利用导数研究函数的单调性从而求出函数的最值.
3.【答案】A
【解析】由,知,即,
∴锐角,
故,
又,
∴,故f(x)是将向左平移个单位长度得到,故选A.
【点评】由辅助角公式化简已知条件求锐角,根据f(x)的函数式,应用二倍角、诱导公式将f(x)化为正弦型函数,即可判断图象的平移方式.
4.【答案】A
【解析】由图象知,,∴T=2π,则,
∴fx=2sinx+φ,
将点的坐标代入得,,即,
又,∴,则,
将fx的图象向左平移个单位得到函数,
∴gx在上的最小值为,故选A.
【点评】本题主要考查三角函数图象,需要利用三角函数的周期性以及对称性进行处理,再结合图象的平移,三角函数的单调性进行解题,本题属于中档题.
5.【答案】B
【解析】,
由题意知函数周期为π,则,,
从而,
把函数fx的图象沿x轴向左平移个单位,
横坐标伸长到原来的2倍得到函数,
gx不是奇函数,A错;
gx在是单调递增,C错;
时,函数gx的值域是[1,2],D错;
gx的图象关于直线对称,B对,
只有选项B正确,故选B.
【点评】本题考查三角函数,图象的变换,以及图象的性质,属于中档题.
6.【答案】A
【解析】,所以c=3,
由余弦定理可得,得a=13,
又由正弦定理可得,所以,故选A.
【点评】本题主要考了三角形的面积公式以及余弦定理公式的运用,属于基础题型.
7.【答案】A
【解析】因为在三角形中,变形为,
由内角和定理可得,
化简可得,,所以,
所以三角形为钝角三角形,故选A.
【点评】本题考查了解三角形,主要是公式的变形是解题的关键,属于较为基础题.
二、填空题.
8.【答案】
【解析】,
因为,所以,
因此由,
而,把代入(1)得:
,而,
因此,故答案为.
【点评】本题考查了三角恒等变换与三角函数求值问题,是基础题.
9.【答案】
【解析】由三角函数的定义可得,,
因此,,
故答案为.
【点评】本题考查任意角的三角函数的应用,诱导公式的应用,是基本知识的考查.
三、解答题.
10.【答案】(1);(2).
【解析】(1),
令,,,
由y=sinU的图象知,,即,
,所以函数f(x)的值域为.
(2),
∵f(ωx)=3,,即,
∵x∈0,π,,
且或,
由于方程f(ωx)=3(ω>0)在区间0,π上至少有两个不同的解,
所以,解得,
所以ω的取值范围为.
【点评】考查三角函数的值域时,常用的方法:
(1)将函数化简整理为f(x)=Asinωx+φ,再利用三角函数性质求值域;
(2)利用导数研究三角函数的单调区间,从而求出函数的最值.
11.【答案】(1)递增区间为,,递减区间为;(2).
【解析】(1)由题意得
,
因为,所以,
令,解得;
令,解得;
令,得.
所以函数fx在上的单调递增区间为,,
单调递减区间为.
(2)由(1)知.
因为,所以,
又因为,所以,
所以.
【点评】三角函数的化简求值的规律总结:
1.给角求值:一般给出的角是非特殊角,要观察所给角与特殊角的关系,利用三角变换转化为求特殊角的三角函数值问题;
2.给值求值:即给出某些角的三角函数值,求另外一些角的三角函数值,解题关键在于“变角”,使相关角相同或具有某种关系;
3.给值求角:实质上可转化为“给值求值”即通过求角的某个三角函数值来求角(注意角的范围).
12.【答案】(1);(2).
【解析】(1)在△ABD中,由余弦定理可得,
∵CD//AB,∴∠BDC=∠ABD,
在△BCD中,由余弦定理可得,.
(2)设BC=x,则AB=2x,
在△ABD中,,
在△BCD中,,
由(1)可知,∠BDC=∠ABD,所以,cos∠BDC=cos∠ABD,即,
整理可得x2+2x-2=0,
因为x>0,解得x=3-1,
因此,.
【点评】在解三角形的问题中,若已知条件同时含有边和角,但不能直接使用正弦定理或余弦定理得到答案,要选择“边化角”或“角化边”,变换原则如下:
(1)若式子中含有正弦的齐次式,优先考虑正弦定理“角化边”;
(2)若式子中含有a、b、c的齐次式,优先考虑正弦定理“边化角”;
(3)若式子中含有余弦的齐次式,优先考虑余弦定理“角化边”;
(4)代数式变形或者三角恒等变换前置;
(5)含有面积公式的问题,要考虑结合余弦定理求解;
(6)同时出现两个自由角(或三个自由角)时,要用到三角形的内角和定理.
13.【答案】(1);(2)3.
【解析】(1)在三角形ABC中,∵2b-ccosA=acosC,
由正弦定理得,
化为:,
三角形中,解得,A∈0,π,
∴.
(2)由余弦定理得,
∵a=13,b+c=5,
∴13=b+c2-3cb=52-3bc,化为bc=4,
所以三角形ABC的面积.
【点评】本题考查正余弦定理和三角形面积公式的综合运用,涉及三角函数恒等变换,属基础题.熟练掌握利用正弦定理边化角,并结合三角函数两角和差公式化简,注意余弦定理与三角形面积公式的综合运用.
14.【答案】(1);(2)6+23.
【解析】(1)∵asin(A+B-C)=csin(B+C),,
,
,,,.
(2)由题意可得,∴ab=8,
∵2a+b=8联立可得,a=2,b=4,
由余弦定理可得c2=12,c=23,此时周长为6+23.
【点评】本题主要考查了三角形的内角及诱导公式在三角形化简中的应用,还考查了三角形的面积公式及余弦定理,属于基础题.
15.【答案】(1)证明见解析;(2).
【解析】(1)由2csinB=3asinC,
根据正弦定理可得2cb=3ac,所以2b=3a,则,
又,根据余弦定理可得,
则,所以,
因此△ABC为等腰三角形.
(2)因为角C是三角形内角,所以sinC>0,则,
因为△ABC面积为22,
所以,解得a=2,所以b=c=3,
又D为AB中点,所以,
则,整理得,所以.
【点评】本题主要考查正余弦定理、三角形的面积公式的综合运用,利用正弦定理进行边角转换等,
属于中档题型.
16.【答案】(1);(2).
【解析】(1)因为,由正弦定理得,
因为sinC≠0,所以,所以,
因为,所以,
所以,即,所以.
(2)设△ABD的AB边上的高为h1,△ADC的AC边上的高为h2,
因为,c=3,b=1,所以,
所以h1=h2,AD是△ABC角A的内角平分线,所以,
因为S△ABD=3S△ADC,可知,
所以,所以.
【点评】关键点点睛:本题考查了正弦定理的边角互化、三角形的面积公式,解题的关键是确定AD是△ABC角A的内角平分线,考查了运算能力.
高频易错题
高频易错题
一、选择题.
1.【答案】C
【解析】将的图象向左平移个单位得,
再所得图象上各点的横坐标缩短为原来的倍,纵坐标不变,得到,
故选C.
【点评】在三角函数平移变换中,y=sinωx向左平移个单位得到的函数解析式为y=sinωx+φ=sinωx+ωφ,而不是y=sinωx+,考查运算求解能力,是基础题.
二、填空题.
2.【答案】(22,23)
【解析】由,得b=4cosA,由,
,故,
所以,所以b=4cosA∈22,23.
【点评】该题考查的是有关解三角形的问题,涉及到的知识点有正弦定理,以及锐角三角形的条件,属于简单题目.
精准预测题
精准预测题
一、选择题.
1.【答案】A
【解析】由图可知,,
所以,故选A.
【点评】本题考查运用向量进行余弦定理的证明,属于基础题型.
2.【答案】C
【解析】因为,
利用诱导公式可得,即,
所以,故选C.
【点评】本题主要考查诱导公式,正切的两角和差公式的应用,属于基础题.
二、解答题.
3.【答案】(1);(2)-1,2.
【解析】(1),
因为,所以,
即,所以-33sinα=cosα,所以.
(2)f(x)图象上所有点横坐标变为原来的倍得到函数g(x)的图象,
所以g(x)的解析式为,
因为,所以,则,
所以-1≤g(x)≤2,
故g(x)在上的值域为-1,2.
【点评】本题主要考查三角恒等变换,同角三角函数的基本关系,函数y=Asinωx+φ的图象变换规律,正弦函数的定义域和值域,属于中档题.
4.【答案】(1)π,-43+1,43+1(2)(3+3,33].
【解析】(1)
,
,值域为-43+1,43+1.
(2)由f(A)=-5,可得,
因为三角形为锐角△ABC,
所以,即,,
由正弦定理,得,,
所以
.
因为△ABC为锐角三角形,所以,,
即,解得,
所以,,即,
所以周长的取值范围为区间(3+3,33].
【点评】在解三角形的周长范围时,将a+b+c转化为含一个角的三角函数问题,利用三角函数的值域,
求周长的取值范围,是常用解法.
同课章节目录
