新高考数学二轮专题复习(艺体生专用)专题三向量课件(53页例PPT)
文档属性
| 名称 | 新高考数学二轮专题复习(艺体生专用)专题三向量课件(53页例PPT) | 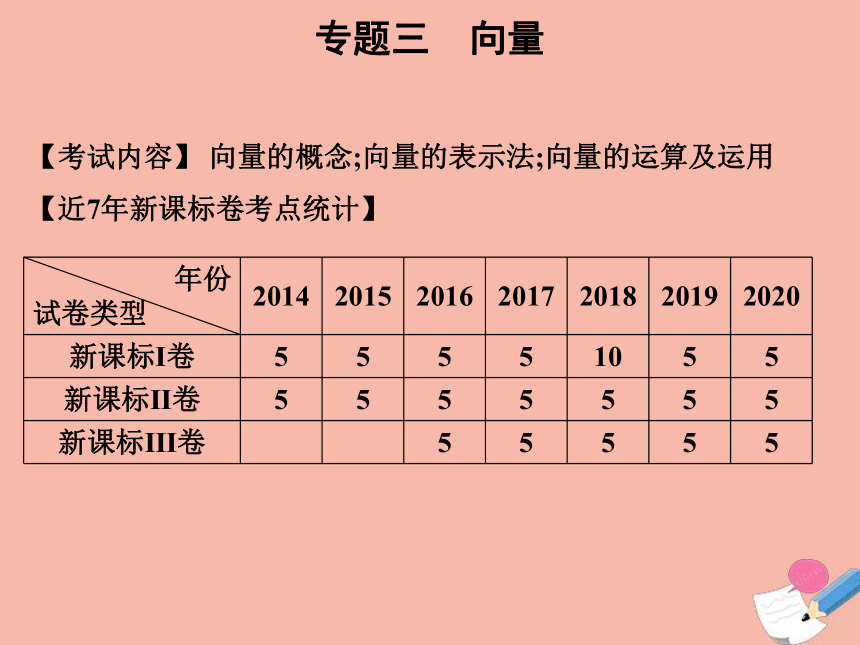 | |
| 格式 | pptx | ||
| 文件大小 | 770.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 17:59:31 | ||
图片预览











文档简介
专题三 向量
【考试内容】 向量的概念;向量的表示法;向量的运算及运用
【近7年新课标卷考点统计】
年份
试卷类型
2014
2015
2016
2017
2018
2019
2020
新课标Ⅰ卷
5
5
5
5
10
5
5
新课标Ⅱ卷
5
5
5
5
5
5
5
新课标Ⅲ卷
5
5
5
5
5
重要考点回顾
一、平面向量
(一)向量的概念
1.向量:既有大小又有方向的量,向量不能比较大小,但向量的模可以比较大小.
2.零向量:长度为0的向量,记为 ,其方向是任意的, 与任意向量平行.
3.单位向量:模为1个单位长度的向量.
4.平行向量(共线向量):方向相同或相反的非零向量.
5.相等向量:长度相等且方向相同的向量.
(二)向量的表示
1.几何表示:用一条有向线段表示向量.如 或a,b等.
2.坐标表示:在平面直角坐标系中,设向量 的起点O为坐标原点,终点A坐标为(x,y),
则(x,y)称为 的坐标,记为 =(x,y).
当向量起点不在原点时,向量 坐标为终点坐标减去起点坐标,即若A(x1,y1),B(x2,y2),
则 =(x2-x1,y2-y1).
注:向量既有代数特征,又有几何特征,它是数形兼备的好工具.
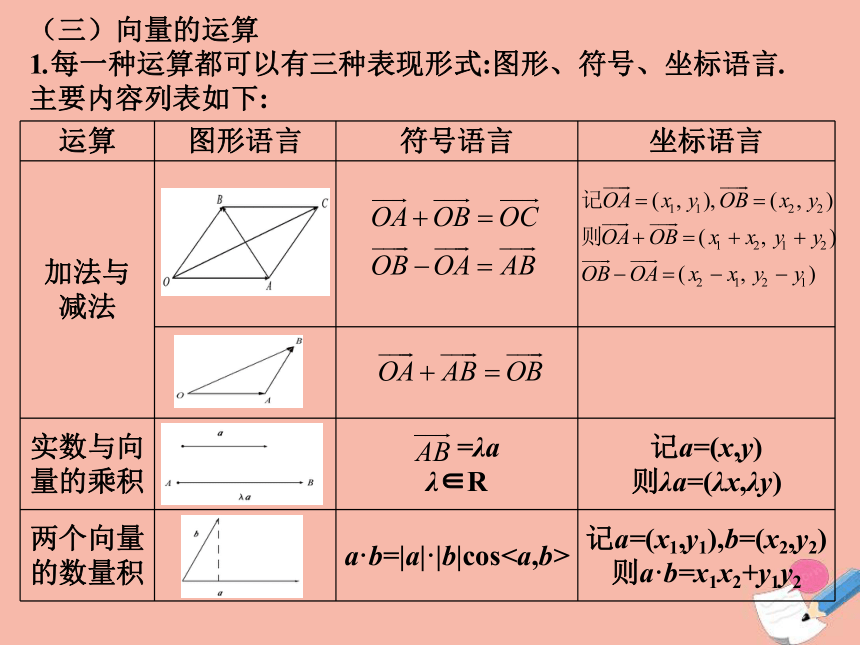
(三)向量的运算
1.每一种运算都可以有三种表现形式:图形、符号、坐标语言.
主要内容列表如下:
运算
图形语言
符号语言
坐标语言
加法与
减法
实数与向量的乘积
=λa
λ∈R
记a=(x,y)
则λa=(λx,λy)
两个向量的数量积
a·b=|a|·|b|cos
记a=(x1,y1),b=(x2,y2)
则a·b=x1x2+y1y2
2.向量的运算律
加法:①a+b=b+a(交换律);②(a+b)+c=a+(b+c)(结合律)
实数与向量的乘积:①λ(a+b)=λa+λb;②(λ+μ)a=λa+μa;
③λ(μa)=(λμ)a
两个向量的数量积:①a·b=b·a;②(λa)·b=a·(λb)=λ(a·b);
③(a+b)·c=a·c+b·c
注意:根据向量运算律可知,两个向量之间的线性运算满足实数多项式乘积的运算法则,正确迁移实数的运算性质可以简化向量的运算,
例如(a±b)2=a2±2a·b+b2
3.两个向量数量积的重要性质:
①a2=|a|2即|a|= (求线段的长度);
②求向量的夹角:已知两个非零向量a与b,作
则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角,
cosθ=cos=
特别注意:当且仅当两个非零向量a与b同方向时,θ=0°,当且仅当a与b反方向时θ=180°,同时 与其他任何非零向量之间不谈夹角这一问题.
(四)向量的应用
1.两个向量平行的充要条件
符号语言:a∥b?a=λb(b≠ )
坐标语言为:设非零向量a=(x1,y1),b=(x2,y2),则a∥b?(x1,y1)=λ(x2,y2)?x1y2-x2y1=0
2.两个向量垂直的充要条件
符号语言:a⊥b?a·b=0
坐标语言:设非零向量a=(x1,y1),b=(x2,y2),则a⊥b?x1x2+y1y2=0
二、空间向量
(一)空间向量及其运算
1.空间向量的有关概念
(1)空间向量:在空间中,具有大小和方向的量;
(2)相等向量:方向相同且模相等的向量;
(3)共线向量:表示空间向量的有向线段所在的直线互相平行或重合;
(4)共面向量:平行于同一平面的向量.
2.空间向量中的有关定理
(1)共线向量定理:对空间任意两个向量a,b(b≠0),a∥b?存在λ∈R,使a=λb;
(2)共面向量定理:若两个向量a,b不共线,则向量p与向量a,b共面?存在唯一的有序实数对(x,y)使p=xa+yb;
(3)空间向量基本定理:如果三个向量a,b,c不共面,那么对空间任一向量p,存在一个唯一的有序实数组{x,y,z}使得p=xa+yb+zc,其中{a,b,c}叫做空间的一个基底.
3.两个向量的数量积
(1)非零向量a,b的数量积a·b=|a||b|cos.
(2)空间向量数量积的运算律
①结合律:(λa)·b=λ(a·b);
②交换律:a·b=b·a;
③分配律:a·(b+c)=a·b+a·c.
4.空间向量的坐标表示及其应用
设向量a=(x1,y1,z1),b=(x2,y2,z2),则
(1)a+b=(x1+x2,y1+y2,z1+z2);
(2)a-b=(x1-x2,y1-y2,z1-z2);
(3)λa=(λx1,λy1,λz1);
(4)a·b=x1x2+y1y2+z1z2;
(5)若a,b为非零向量,且a⊥b?a·b=0?x1x2+y1y2+z1z2=0;
(6)若b≠0,且a∥b?a=λb?x1=λx2,y1=λy2,z1=λz2;
(7)|a|= = ;
(8)cos=
(9)点A=(x1,y1,z1),B=(x2,y2,z2),
则dAB=| |=
(10)共面向量定理:p,a,b共面?p=xa+yb(x,y∈R);
P,A,B,C四点共面
(11)空间向量基本定理p=xa+yb+zc(x,y,z∈R)(不共面的三个向量a,b,c构成一组基底,任意两个向量都共面).
(二)立体几何中的向量方法
1.设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为u,v,则
(1)平行:
线线平行:m∥l?a∥b?a=kb(k∈R且k≠0)
线面平行:l∥α?a⊥u?a·u=0
面面平行:α∥β?u∥v?u=kv(k∈R且k≠0)
(2)垂直:
线线垂直:l⊥m?a⊥b?a·b=0
线面垂直:l⊥α?a∥u?u=ka(k∈R且k≠0)
面面垂直:α⊥β?u⊥v?u·v=0
2.空间角的求法
(1)异面直线所成的角
设a,b分别是两异面直线l1,l2的方向向量,则
(2)求直线与平面所成的角
设直线l的方向向量为a,平面α的法向量为n,直线l与平面α所成的角为θ,则sin θ=|cos|=
a与b的夹角β
l1与l2所成的角θ
范围
(0,π)
求法
(3)求二面角的大小
①如图①,AB,CD分别是二面角α-l-β的两个面内与棱l垂直的直线,则二面角的大小θ=< >.
① ② ③
②如图②③,n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小θ满足|cos θ|=|cos|,二面角的平面角大小是向量n1与n2的夹角(或其补角).
1.已知点A(0,1),B(3,2),向量 =(-4,-3),则向量 = ( )
A.(-7,-4) B.(7,4) C.(-1,4) D.(1,4)
2.若向量a,b满足|a|=|b|=1,a与b的夹角为60°,则a·a+a·b= ( )
考点训练
3.若向量a=(1,1),b=(2,5),c=(3,x)满足条件(8a-b)·c=30,则x=( )
A.6 B.5 C.4 D.3
4.如图,设P是△ABC所在平面内的一点, ,则( )
5.如图,△ABC中,AB边的高为CD,若 ,a·b=0,|a|=1,
|b|=2,则 ( )
6.已知向量a=(1,0),b=(0,1),c=ka+b(k∈R),d=a-b,如果c∥d那么( )
A.k=1且c与d同向 B.k=1且c与d反向
C.k=-1且c与d同向 D.k=-1且c与d反向
7.设x∈R,向量a=(x,1),b=(1,-2),且a⊥b,则|a+b|= ( )
8.若向量a、b满足|a|=1,|b|=2,且a与b的夹角为 ,则|a+b|= .
9.已知|a|=3,|b|=2.若a·b=-3,则a与b夹角的大小为 .
10.已知向量a=(2,1),a·b=10,|a+b|= ,则|b|= ( )
A. B. C.5 D.25
11.平面向量a与b的夹角为60°,a=(2,0),|b|=1,则|a+2b|= ( )
A. B.2 C.4 D.12
12.已知向量a=(1,2),b=(-2,m),且a∥b,则2a+3b= ( )
A.(-5,-10) B.(-4,-8) C.(-3,-6) D.(-2,-4)
13.已知向量 ,则∠ABC= ( )
A.30° B.45° C.60° D.120°
14.向量a=(1,2),b=(1,0),c=(3,4).若λ为实数,(a+λb)∥c则λ= ( )
A. B. C.1 D.2
15.已知向量a=(1,0),b=(1,1),则与2a+b同向的单位向量的坐标表示为 .
16.设a、b都是非零向量,下列四个条件中,使 成立的充分条件是 ( )
A.|a|=|b|且a∥b B.a=-b C.a∥b D.a=2b
17.已知向量a=(1,2),b=(2,-3).若向量c满足(c+a)∥b,c⊥(a+b),
则c= ( )
18.已知平面向量a=(1,-3),b=(4,-2),λa+b与a垂直,则λ= ( )
A.-1 B.1 C.-2 D.2
19.设向量a=(1,cosθ)与b=(-1,2cosθ)垂直,则cos2θ等于 ( )
A. B. C.0 D.-1
20.已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 的值为( )
21.空间直角坐标系中,已知点P(3,-2,-5),点Q与点P关于平面xOz对称,则点Q的坐标是 ( )
A.(-3,2,5) B.(3,-2,5) C.(3,2,-5) D.(-3,-2,-5)
{2D5ABB26-0587-4C30-8999-92F81FD0307C}C 【解析】空间直角坐标系中,点P(3,-2,-5),
∵点Q与点P关于平面xOz对称,∴Q点的坐标是(3,2,-5).故选C.
22.已知直线l的一个方向向量m=(2,-1,3),且直线l过A(0,y,3)和
B(-1,2,z)两点,则y-z= ( )
A.0 B.1 C. D.3
23.已知向量a=(λ+1,0,2),b=(6,2μ-1,2λ).若a∥b,则λ与μ的值可以是 ( )
24.在三棱锥P-ABC中,M为PA的中点,N在BC上,且BN=2NC,则( )
25.若向量a=(2,-3,1)和b=(1,x,4)满足条件a·b=0,则x的值是( )
A.-1 B.0 C.1 D.2
{2D5ABB26-0587-4C30-8999-92F81FD0307C}D 【解析】因为向量a=(2,-3,1)和b=(1,x,4)满足条件a·b=0,
即2-3x+4=0,解得x=2.故选D.
26.在下列条件中,使点M与A,B,C一定共面的是 ( )
28.已知空间三点A(0,1,2),B(1,3,5),C(2,5,4-k)在一条直线上,则实数k的值是 ( )
A.2 B.4 C.-4 D.-2
29.已知向量a=(0,3,3)和b=(-1,1,0)分别是直线l和m的方向向量,则直线l与m所成的角为 ( )
30.若向量a=(1,-1,2),b=(2,1,-3),则|a+b|= ( )
31.长方体ABCD -A1B1C1D1的底面是边长为1的正方形,高为2,M,N分别是四边形BB1C1C和正方形A1B1C1D1的中心,则向量 与 的夹角的余弦值是 ( )
32.若直线l的方向向量m=(x,-1,2),平面α的法向量n=(-2,-2,4),且直线l⊥平面α,则实数x的值是 ( )
A.1 B.5 C.-1 D.-5
33.已知向量a=(-2,1,3),b=(-1,2,1)若a⊥(a-λb),则实数λ的值为( )
{2D5ABB26-0587-4C30-8999-92F81FD0307C}D 【解析】 a-λb=(-2+λ,1-2λ,3-λ).
∵a⊥(a-λb),∴a·(a-λb)=-2(-2+λ)+(1-2λ)+3(3-λ)=0.
解得实数λ=2.故选D.
34.已知向量a=(0,2,1),b=(-1,1,m),若a,b分别是平面α,β的法向量,且α⊥β,则m= ( )
A.-1 B.1 C.-2 D.2
{2D5ABB26-0587-4C30-8999-92F81FD0307C}C 【解析】 ∵向量a=(0,2,1),b=(-1,1,m),a,b分别是平面α,β的法向量,且α⊥β,
∴a·b=2+m=0,解得m=-2.故选C.
35.在长方体ABCD -A1B1C1D1中,AB=BC=2,AA1=1,则直线BC1与平面BB1D1D所成角的正弦值为 ( )
36.《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如下图,在鳖臑中P -ABC,PA⊥平面ABC,AB⊥BC,且PA=AB=
BC=1,则二面角A-PC-B的大小是 ( )
A.30° B.45° C.60° D.90°
37.(多选题)在△ABC中,AB=AC,BC=4,D为BC的中点,则以下结论正确的是 ( )
38.(多选题)已知向量a=(2,-1),b=(-3,2),c=(1,1),则 ( )
A.a∥b B.(a+b)⊥c C.a+b=c D.c=5a+3b
39.(多选题)已知正方形ABCD的边长为2,向量a,b满足 =2a,
=2a+b,则 ( )
A.|b|= B.a⊥b C.a·b=2 D.(4a+b)⊥b
41.(多选题)若a,b,c是任意的非零向量,则下列叙述正确的是( )
A.若a=b,则|a|=|b| B.若a·c=b·c,则a=b
C.若a∥b,b∥c,则a∥c D.若|a+b|=|a-b|,则a⊥b
{2D5ABB26-0587-4C30-8999-92F81FD0307C}ACD 【解析】 对于A,若a=b,则向量a,b长度相等,方向相同,故|a|=|b|,故A正确;
对于B,当a⊥c且b⊥c时,a·c=b·c=0,但a,b可以不相等,故B错误;
对于C,若a∥b,b∥c,则a,b方向相同或相反,b,c方向相同或相反,故a,c的方向相同或相反,故a∥c,故C正确;
对于D,若|a+b|=|a-b|,则a2+2a·b+b2=a2-2a·b+b2,即a·b=0,则a⊥b,故D正确.故选ACD.
42.(多选题)若向量a=(-1,λ,-2),b=(2,-1,1),a与b的夹角为120°,则λ的值为 ( )
A.17 B.-17 C.-1 D.1
43.(多选题)已知向量a=(1,2,3),b=(3,0,-1),c=(-1,5,-3)下列等式中正确的是 ( )
A.(a·b)c=b·c B.(a+b)·c=a·(b+c)
C.(a+b+c)2=a2+b2+c2 D.|a+b+c|=|a-b-c|
44.(多选题)已知v为直线l的方向向量,n1,n2分别为平面α,β的法向量(α,β不重合),那么下列选项中,正确的是 ( )
A.n1∥n2?α∥β B.n1⊥n2?α⊥β
C.v∥n1?l∥α D.v⊥n1?l∥α
{2D5ABB26-0587-4C30-8999-92F81FD0307C}AB 【解析】 v为直线l的方向向量,
n1,n2分别为平面α,β的法向量(α,β不重合),
则n1∥n2?α∥β,n1⊥n2?α⊥β,
v∥n1?l⊥α,v⊥n1?l∥α或l?α.
因此AB正确.故选AB.
【考试内容】 向量的概念;向量的表示法;向量的运算及运用
【近7年新课标卷考点统计】
年份
试卷类型
2014
2015
2016
2017
2018
2019
2020
新课标Ⅰ卷
5
5
5
5
10
5
5
新课标Ⅱ卷
5
5
5
5
5
5
5
新课标Ⅲ卷
5
5
5
5
5
重要考点回顾
一、平面向量
(一)向量的概念
1.向量:既有大小又有方向的量,向量不能比较大小,但向量的模可以比较大小.
2.零向量:长度为0的向量,记为 ,其方向是任意的, 与任意向量平行.
3.单位向量:模为1个单位长度的向量.
4.平行向量(共线向量):方向相同或相反的非零向量.
5.相等向量:长度相等且方向相同的向量.
(二)向量的表示
1.几何表示:用一条有向线段表示向量.如 或a,b等.
2.坐标表示:在平面直角坐标系中,设向量 的起点O为坐标原点,终点A坐标为(x,y),
则(x,y)称为 的坐标,记为 =(x,y).
当向量起点不在原点时,向量 坐标为终点坐标减去起点坐标,即若A(x1,y1),B(x2,y2),
则 =(x2-x1,y2-y1).
注:向量既有代数特征,又有几何特征,它是数形兼备的好工具.
(三)向量的运算
1.每一种运算都可以有三种表现形式:图形、符号、坐标语言.
主要内容列表如下:
运算
图形语言
符号语言
坐标语言
加法与
减法
实数与向量的乘积
=λa
λ∈R
记a=(x,y)
则λa=(λx,λy)
两个向量的数量积
a·b=|a|·|b|cos
记a=(x1,y1),b=(x2,y2)
则a·b=x1x2+y1y2
2.向量的运算律
加法:①a+b=b+a(交换律);②(a+b)+c=a+(b+c)(结合律)
实数与向量的乘积:①λ(a+b)=λa+λb;②(λ+μ)a=λa+μa;
③λ(μa)=(λμ)a
两个向量的数量积:①a·b=b·a;②(λa)·b=a·(λb)=λ(a·b);
③(a+b)·c=a·c+b·c
注意:根据向量运算律可知,两个向量之间的线性运算满足实数多项式乘积的运算法则,正确迁移实数的运算性质可以简化向量的运算,
例如(a±b)2=a2±2a·b+b2
3.两个向量数量积的重要性质:
①a2=|a|2即|a|= (求线段的长度);
②求向量的夹角:已知两个非零向量a与b,作
则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角,
cosθ=cos
特别注意:当且仅当两个非零向量a与b同方向时,θ=0°,当且仅当a与b反方向时θ=180°,同时 与其他任何非零向量之间不谈夹角这一问题.
(四)向量的应用
1.两个向量平行的充要条件
符号语言:a∥b?a=λb(b≠ )
坐标语言为:设非零向量a=(x1,y1),b=(x2,y2),则a∥b?(x1,y1)=λ(x2,y2)?x1y2-x2y1=0
2.两个向量垂直的充要条件
符号语言:a⊥b?a·b=0
坐标语言:设非零向量a=(x1,y1),b=(x2,y2),则a⊥b?x1x2+y1y2=0
二、空间向量
(一)空间向量及其运算
1.空间向量的有关概念
(1)空间向量:在空间中,具有大小和方向的量;
(2)相等向量:方向相同且模相等的向量;
(3)共线向量:表示空间向量的有向线段所在的直线互相平行或重合;
(4)共面向量:平行于同一平面的向量.
2.空间向量中的有关定理
(1)共线向量定理:对空间任意两个向量a,b(b≠0),a∥b?存在λ∈R,使a=λb;
(2)共面向量定理:若两个向量a,b不共线,则向量p与向量a,b共面?存在唯一的有序实数对(x,y)使p=xa+yb;
(3)空间向量基本定理:如果三个向量a,b,c不共面,那么对空间任一向量p,存在一个唯一的有序实数组{x,y,z}使得p=xa+yb+zc,其中{a,b,c}叫做空间的一个基底.
3.两个向量的数量积
(1)非零向量a,b的数量积a·b=|a||b|cos
(2)空间向量数量积的运算律
①结合律:(λa)·b=λ(a·b);
②交换律:a·b=b·a;
③分配律:a·(b+c)=a·b+a·c.
4.空间向量的坐标表示及其应用
设向量a=(x1,y1,z1),b=(x2,y2,z2),则
(1)a+b=(x1+x2,y1+y2,z1+z2);
(2)a-b=(x1-x2,y1-y2,z1-z2);
(3)λa=(λx1,λy1,λz1);
(4)a·b=x1x2+y1y2+z1z2;
(5)若a,b为非零向量,且a⊥b?a·b=0?x1x2+y1y2+z1z2=0;
(6)若b≠0,且a∥b?a=λb?x1=λx2,y1=λy2,z1=λz2;
(7)|a|= = ;
(8)cos
(9)点A=(x1,y1,z1),B=(x2,y2,z2),
则dAB=| |=
(10)共面向量定理:p,a,b共面?p=xa+yb(x,y∈R);
P,A,B,C四点共面
(11)空间向量基本定理p=xa+yb+zc(x,y,z∈R)(不共面的三个向量a,b,c构成一组基底,任意两个向量都共面).
(二)立体几何中的向量方法
1.设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为u,v,则
(1)平行:
线线平行:m∥l?a∥b?a=kb(k∈R且k≠0)
线面平行:l∥α?a⊥u?a·u=0
面面平行:α∥β?u∥v?u=kv(k∈R且k≠0)
(2)垂直:
线线垂直:l⊥m?a⊥b?a·b=0
线面垂直:l⊥α?a∥u?u=ka(k∈R且k≠0)
面面垂直:α⊥β?u⊥v?u·v=0
2.空间角的求法
(1)异面直线所成的角
设a,b分别是两异面直线l1,l2的方向向量,则
(2)求直线与平面所成的角
设直线l的方向向量为a,平面α的法向量为n,直线l与平面α所成的角为θ,则sin θ=|cos
a与b的夹角β
l1与l2所成的角θ
范围
(0,π)
求法
(3)求二面角的大小
①如图①,AB,CD分别是二面角α-l-β的两个面内与棱l垂直的直线,则二面角的大小θ=< >.
① ② ③
②如图②③,n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小θ满足|cos θ|=|cos
1.已知点A(0,1),B(3,2),向量 =(-4,-3),则向量 = ( )
A.(-7,-4) B.(7,4) C.(-1,4) D.(1,4)
2.若向量a,b满足|a|=|b|=1,a与b的夹角为60°,则a·a+a·b= ( )
考点训练
3.若向量a=(1,1),b=(2,5),c=(3,x)满足条件(8a-b)·c=30,则x=( )
A.6 B.5 C.4 D.3
4.如图,设P是△ABC所在平面内的一点, ,则( )
5.如图,△ABC中,AB边的高为CD,若 ,a·b=0,|a|=1,
|b|=2,则 ( )
6.已知向量a=(1,0),b=(0,1),c=ka+b(k∈R),d=a-b,如果c∥d那么( )
A.k=1且c与d同向 B.k=1且c与d反向
C.k=-1且c与d同向 D.k=-1且c与d反向
7.设x∈R,向量a=(x,1),b=(1,-2),且a⊥b,则|a+b|= ( )
8.若向量a、b满足|a|=1,|b|=2,且a与b的夹角为 ,则|a+b|= .
9.已知|a|=3,|b|=2.若a·b=-3,则a与b夹角的大小为 .
10.已知向量a=(2,1),a·b=10,|a+b|= ,则|b|= ( )
A. B. C.5 D.25
11.平面向量a与b的夹角为60°,a=(2,0),|b|=1,则|a+2b|= ( )
A. B.2 C.4 D.12
12.已知向量a=(1,2),b=(-2,m),且a∥b,则2a+3b= ( )
A.(-5,-10) B.(-4,-8) C.(-3,-6) D.(-2,-4)
13.已知向量 ,则∠ABC= ( )
A.30° B.45° C.60° D.120°
14.向量a=(1,2),b=(1,0),c=(3,4).若λ为实数,(a+λb)∥c则λ= ( )
A. B. C.1 D.2
15.已知向量a=(1,0),b=(1,1),则与2a+b同向的单位向量的坐标表示为 .
16.设a、b都是非零向量,下列四个条件中,使 成立的充分条件是 ( )
A.|a|=|b|且a∥b B.a=-b C.a∥b D.a=2b
17.已知向量a=(1,2),b=(2,-3).若向量c满足(c+a)∥b,c⊥(a+b),
则c= ( )
18.已知平面向量a=(1,-3),b=(4,-2),λa+b与a垂直,则λ= ( )
A.-1 B.1 C.-2 D.2
19.设向量a=(1,cosθ)与b=(-1,2cosθ)垂直,则cos2θ等于 ( )
A. B. C.0 D.-1
20.已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 的值为( )
21.空间直角坐标系中,已知点P(3,-2,-5),点Q与点P关于平面xOz对称,则点Q的坐标是 ( )
A.(-3,2,5) B.(3,-2,5) C.(3,2,-5) D.(-3,-2,-5)
{2D5ABB26-0587-4C30-8999-92F81FD0307C}C 【解析】空间直角坐标系中,点P(3,-2,-5),
∵点Q与点P关于平面xOz对称,∴Q点的坐标是(3,2,-5).故选C.
22.已知直线l的一个方向向量m=(2,-1,3),且直线l过A(0,y,3)和
B(-1,2,z)两点,则y-z= ( )
A.0 B.1 C. D.3
23.已知向量a=(λ+1,0,2),b=(6,2μ-1,2λ).若a∥b,则λ与μ的值可以是 ( )
24.在三棱锥P-ABC中,M为PA的中点,N在BC上,且BN=2NC,则( )
25.若向量a=(2,-3,1)和b=(1,x,4)满足条件a·b=0,则x的值是( )
A.-1 B.0 C.1 D.2
{2D5ABB26-0587-4C30-8999-92F81FD0307C}D 【解析】因为向量a=(2,-3,1)和b=(1,x,4)满足条件a·b=0,
即2-3x+4=0,解得x=2.故选D.
26.在下列条件中,使点M与A,B,C一定共面的是 ( )
28.已知空间三点A(0,1,2),B(1,3,5),C(2,5,4-k)在一条直线上,则实数k的值是 ( )
A.2 B.4 C.-4 D.-2
29.已知向量a=(0,3,3)和b=(-1,1,0)分别是直线l和m的方向向量,则直线l与m所成的角为 ( )
30.若向量a=(1,-1,2),b=(2,1,-3),则|a+b|= ( )
31.长方体ABCD -A1B1C1D1的底面是边长为1的正方形,高为2,M,N分别是四边形BB1C1C和正方形A1B1C1D1的中心,则向量 与 的夹角的余弦值是 ( )
32.若直线l的方向向量m=(x,-1,2),平面α的法向量n=(-2,-2,4),且直线l⊥平面α,则实数x的值是 ( )
A.1 B.5 C.-1 D.-5
33.已知向量a=(-2,1,3),b=(-1,2,1)若a⊥(a-λb),则实数λ的值为( )
{2D5ABB26-0587-4C30-8999-92F81FD0307C}D 【解析】 a-λb=(-2+λ,1-2λ,3-λ).
∵a⊥(a-λb),∴a·(a-λb)=-2(-2+λ)+(1-2λ)+3(3-λ)=0.
解得实数λ=2.故选D.
34.已知向量a=(0,2,1),b=(-1,1,m),若a,b分别是平面α,β的法向量,且α⊥β,则m= ( )
A.-1 B.1 C.-2 D.2
{2D5ABB26-0587-4C30-8999-92F81FD0307C}C 【解析】 ∵向量a=(0,2,1),b=(-1,1,m),a,b分别是平面α,β的法向量,且α⊥β,
∴a·b=2+m=0,解得m=-2.故选C.
35.在长方体ABCD -A1B1C1D1中,AB=BC=2,AA1=1,则直线BC1与平面BB1D1D所成角的正弦值为 ( )
36.《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如下图,在鳖臑中P -ABC,PA⊥平面ABC,AB⊥BC,且PA=AB=
BC=1,则二面角A-PC-B的大小是 ( )
A.30° B.45° C.60° D.90°
37.(多选题)在△ABC中,AB=AC,BC=4,D为BC的中点,则以下结论正确的是 ( )
38.(多选题)已知向量a=(2,-1),b=(-3,2),c=(1,1),则 ( )
A.a∥b B.(a+b)⊥c C.a+b=c D.c=5a+3b
39.(多选题)已知正方形ABCD的边长为2,向量a,b满足 =2a,
=2a+b,则 ( )
A.|b|= B.a⊥b C.a·b=2 D.(4a+b)⊥b
41.(多选题)若a,b,c是任意的非零向量,则下列叙述正确的是( )
A.若a=b,则|a|=|b| B.若a·c=b·c,则a=b
C.若a∥b,b∥c,则a∥c D.若|a+b|=|a-b|,则a⊥b
{2D5ABB26-0587-4C30-8999-92F81FD0307C}ACD 【解析】 对于A,若a=b,则向量a,b长度相等,方向相同,故|a|=|b|,故A正确;
对于B,当a⊥c且b⊥c时,a·c=b·c=0,但a,b可以不相等,故B错误;
对于C,若a∥b,b∥c,则a,b方向相同或相反,b,c方向相同或相反,故a,c的方向相同或相反,故a∥c,故C正确;
对于D,若|a+b|=|a-b|,则a2+2a·b+b2=a2-2a·b+b2,即a·b=0,则a⊥b,故D正确.故选ACD.
42.(多选题)若向量a=(-1,λ,-2),b=(2,-1,1),a与b的夹角为120°,则λ的值为 ( )
A.17 B.-17 C.-1 D.1
43.(多选题)已知向量a=(1,2,3),b=(3,0,-1),c=(-1,5,-3)下列等式中正确的是 ( )
A.(a·b)c=b·c B.(a+b)·c=a·(b+c)
C.(a+b+c)2=a2+b2+c2 D.|a+b+c|=|a-b-c|
44.(多选题)已知v为直线l的方向向量,n1,n2分别为平面α,β的法向量(α,β不重合),那么下列选项中,正确的是 ( )
A.n1∥n2?α∥β B.n1⊥n2?α⊥β
C.v∥n1?l∥α D.v⊥n1?l∥α
{2D5ABB26-0587-4C30-8999-92F81FD0307C}AB 【解析】 v为直线l的方向向量,
n1,n2分别为平面α,β的法向量(α,β不重合),
则n1∥n2?α∥β,n1⊥n2?α⊥β,
v∥n1?l⊥α,v⊥n1?l∥α或l?α.
因此AB正确.故选AB.
同课章节目录
