统计与概率课件(共45张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 统计与概率课件(共45张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 551.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 21:27:55 | ||
图片预览








文档简介
(共45张PPT)
统计与概率
真题再研析·提升审题力
考向一 统计
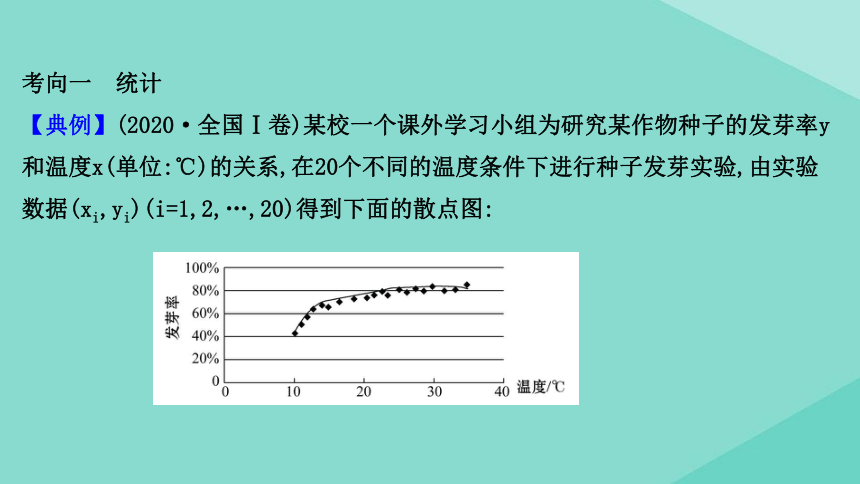
【典例】(2020·全国Ⅰ卷)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是
( )
A.y=a+bx
B.y=a+bx2
C.y=a+bex
D.y=a+bln
x
D 由散点图分布可知,散点图分布在一个对数函数的图象附近,因此,最适合作为发芽率y和温度x的回归方程类型的是y=a+bln
x.
考向二 概率
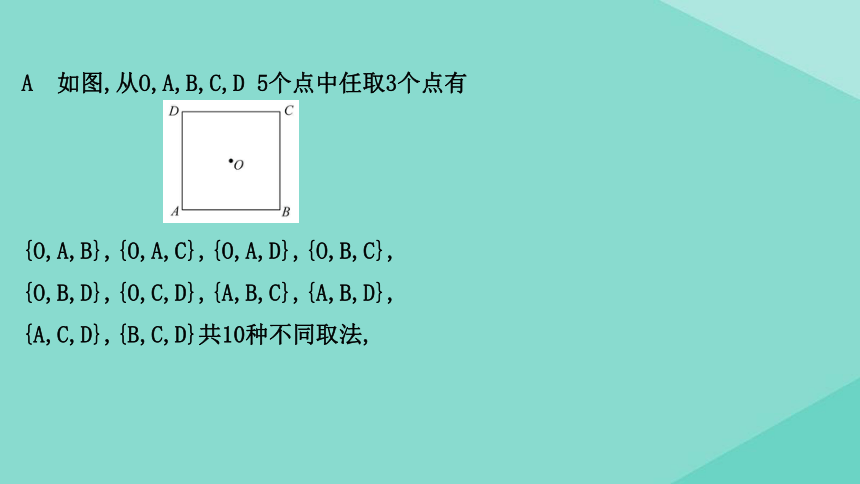
【典例】(2020·全国Ⅰ卷)设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为
( )
A 如图,从O,A,B,C,D
5个点中任取3个点有
{O,A,B},{O,A,C},{O,A,D},{O,B,C},
{O,B,D},{O,C,D},{A,B,C},{A,B,D},
{A,C,D},{B,C,D}共10种不同取法,
3点共线只有{O,A,C}与{O,B,D}共2种情况,
由古典概型的概率计算公式知,
取到3点共线的概率为
【考前必备】
1.线性回归分析的注意点
(1)回归直线一定过样本点的中心(
);
(2)已知样本点不一定在回归直线上;
(3)未知点的求解,通过代入回归直线方程求解即可.
2.独立性检验的注意点
K2的取值的意义有两种表述,当数值表中数值为0.01时,表述为失误率不超过1%的前提下,说两者相关;当数值表中数值为0.99时,表述为有99%的把握,说两者相关.
3.求较复杂的古典概型计算的两种方法
(1)树状图法:当事件个数没有很明显的规律,并且涉及的基本事件又不是太多时,我们可借助树状图法直观地将其表示出来.
(2)图表法:在求概率时,若事件可以表示成有序数对的形式,则可以把全体基本事件用平面直角坐标系中的点表示.
【考场秘技】
1.较复杂的事件的概率可灵活运用互斥事件、对立事件的概率公式简化运算.
2.频数、频率、样本容量的计算方法
(1)
×组距=频率;
(2)
=频率.
3.频率分布直方图中各小长方形的面积之和为1.
【命题陷阱】
1.求回归直线解析式时错用已知数据而不是
求解
【案例】T1要注意.先求出
=100,
=100,然后再求解a的值.
2.频率分布直方图中错把小长方形的高当成概率
【案例】T5求a的值,用概率之和为1的方法求解,应注意的是,每一个小长方形表
示的概率应该是
×组距.
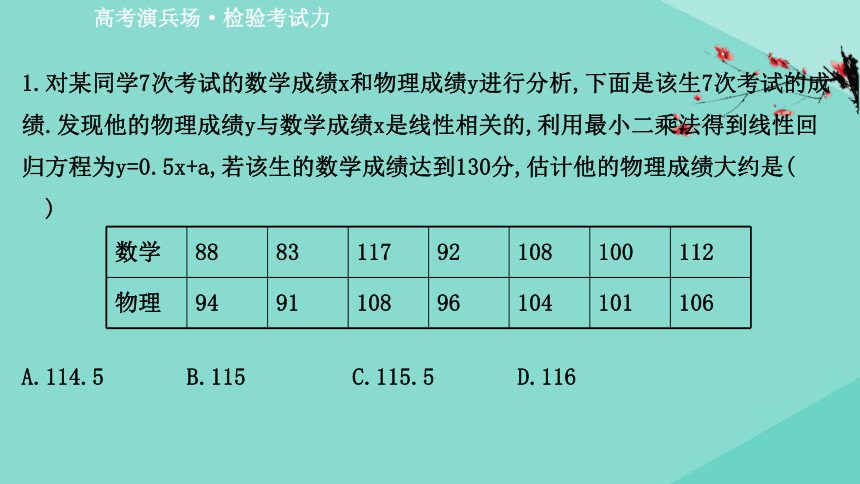
1.对某同学7次考试的数学成绩x和物理成绩y进行分析,下面是该生7次考试的成绩.发现他的物理成绩y与数学成绩x是线性相关的,利用最小二乘法得到线性回归方程为y=0.5x+a,若该生的数学成绩达到130分,估计他的物理成绩大约是( )
A.114.5
B.115
C.115.5
D.116
高考演兵场·检验考试力
数学
88
83
117
92
108
100
112
物理
94
91
108
96
104
101
106
B 由题可知:
=100,
=100,所以a=
-0.5
=100-0.5×100=50,当x=130时,y=0.5×130+50=115.
2.已知两组数据x,y的对应关系如表所示,若根据表中的数据得出y关于x的线性回归方程为y=6.5x+17.5,则表中m的值为
( )
A.50
B.55
C.56.5
D.60
x
2
4
5
6
8
y
30
38
50
m
72
D 由表中数据,计算
=
×(2+4+5+6+8)=5,
=
×(30+38+50+m+72)=38+
,因为回归直线方程y=6.5x+17.5过样本点的
中心,所以38+
=6.5×5+17.5,解得m=60.
3.某班主任对班级51名同学进行了作业量多少的调查,结合数据建立了一个2×2
列联表,可能用到的公式:
可能用到的数据:
P
≈0.01,P
≈0.05,参照以上公式和数据,得到的正确结论
是( )
认为作业多
认为作业不多
总计
喜欢玩电
脑游戏
18
12
30
不喜欢玩
电脑游戏
5
16
21
总计
23
28
51
A.有95%的把握认为喜欢玩电脑游戏与认为作业多少有关
B.有95%的把握认为喜欢玩电脑游戏与认为作业多少无关
C.有99%的把握认为喜欢玩电脑游戏与认为作业多少有关
D.有99%的把握认为喜欢玩电脑游戏与认为作业多少无关
A 根据所给数据可得K2的观测值k=
≈6.535>3.841
,所以
有95%的把握认为喜欢玩电脑游戏与认为作业多少有关.
4.为了检验设备M与设备N的生产效率,研究人员作出统计,得到如表所示的结果,则
( )
设备M
设备N
生产出的合格产品
48
43
生产出的不合格产品
2
7
A.有90%的把握认为生产的产品质量与设备的选择具有相关性
B.没有90%的把握认为生产的产品质量与设备的选择具有相关性
C.可以在犯错误的概率不超过0.01的前提下认为生产的产品质量与设备的选择具有相关性
D.不能在犯错误的概率不超过0.01的前提下认为生产的产品质量与设备的选择具有相关性
A 将题表中的数据代入公式,计算得K2的观测值k=
≈3.053,
因为3.053>2.706,所以有90%的把握认为生产的产品质量与设备的选择具有相关
性.
5.某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1
120名学生中随机抽取了100
名学生的数学成绩,发现都在[80,150]内现将这100名学生的成绩按照
[80,90),[90,100),[100,110),[110,120),[120,130),
[130,140),[140,150]分组后,得到的频率
分布直方图如图所示,则下列说法正确的是
( )
A.频率分布直方图中a的值为
0.040
B.样本数据低于130分的频率为
0.3
C.总体的中位数(保留1位小数)估计为123.3分
D.总体分布在[90,100)的频数一定与总体分布在[100,110)的频数相等
C 由频率分布直方图得:(0.005+0.010+0.010+0.015+a+0.025+0.005)×10=1,
解得a=0.030,故A错误;样本数据低于130分的频率为:1-(0.025+0.005)×10=0.7,
故B错误;[80,120)的频率为:(0.005+0.010+0.010+0.015)×10=0.4,[120,130)
的频率为:0.030×10=0.3.
所以总体的中位数(保留1位小数)估计为:120+
×10≈123.3分,故C正确;
样本分布在[90,100)的频数一定与样本分布在[100,110)的频数相等,总体分布
在[90,100)的频数不一定与总体分布在[100,110)的频数相等,故D错误.
6.如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为
( )
C 从1,2,3,4,5中任取3个不同的数共有{1,2,3},
{1,2,4},{1,2,5},{1,3,4},
{1,3,5},{1,4,5},{2,3,4},{2,3,5},{2,4,5},{3,4,5}10种不同的取法.其中的
勾股数只有{3,4,5},故3个数构成一组勾股数的取法只有1种,故所求概率P=
.
7.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据环保部门某日早6点至晚9点在A县、B县两个地区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,A县、B县两个地区浓度的方差较小的是
( )
A.A县
B.B县
C.A县、B县两个地区相等
D.无法确定
A 根据茎叶图中的数据可知,A县的数据都集中在0.05和0.08之间,数据分布比较稳定,而B县的数据分布比较分散,不如A县数据集中,所以A县的方差较小.
8.
对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.用频率估计概率,现从该批产品中随机抽取一件,则其为二等品的概率为
( )
A.0.09
B.0.20
C.0.25
D.0.45
D 设区间[25,30)对应矩形的另一边长为x,由所有矩形面积之和为1,得(0.02+0.04+0.06+0.03+x)×5=1,解得x=0.05.产品为二等品的概率为0.04×5+0.05×5=0.45.
9.细木棒,长度分别为1,3,5,7,9(cm),从中任取三根,能搭成三角形的概率是
( )
D 设取出的三根木棒能搭成三角形为事件A,任取三根木棒按长度不同共有1、3、
5,1、3、7,1、3、9,1、5、7,1、5、9,1、7、9,3、5、7,3、5、9,3、7、9,5、
7、9,10种情况,由于三角形两边之和大于第三边,构成三角形的只有3、5、7,3、
7、9,5、7、9三种情况,故所求概率为P(A)=
.
10.甲、乙两人参加普法知识竞赛,共有5道不同的题目,其中选择题3道,填空题2道.甲、乙两人依次抽取1道题,则甲抽中选择题、乙抽中填空题的概率等于( )
10.C 记选择题为A,B,C,填空题为d,e.
则甲、乙两人依次抽取,不同的结果有:
(A,B),(A,C),(A,d),(A,e),
(B,A),(B,C),(B,d),(B,e),
(C,A),(C,B),(C,d),(C,e),
(d,A),(d,B),(d,C),(d,e),
(e,A),(e,B),(e,C),(e,d).
共20个.
其中甲抽中选择题、乙抽中填空题的结果有:
(A,d),(A,e),(B,d),(B,e),(C,d),(C,e),共6个.
所以甲抽中选择题、乙抽中填空题的概率P=
11.山东电视台“国学小名士”的播出引发了学校的国学热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“国学达人”的称号,小于85分且不小于70分的学生得到“国学能手”的称号,其他学生得到“国学爱好者”的称号,根据该次比赛的成绩按照称号的不同进行分层抽样,抽选10名学生,则抽选的学生中获得“国学达人”称号的人数为
( )
A.2
B.4
C.5
D.6
A 由茎叶图可得,获“国学达人”称号的有8人,据该次比赛的成绩按照称号的
不同进行分层抽样,抽选10名学生,则抽选的学生中获得“国学达人”称号的人
数为8×
=2.
12.为了研究某班学生的脚长x(单位:厘米)和身高y(单位:厘米)的关系,从该班
随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,
设其回归直线方程为
,已知
=225,
=1
600,
=4.该班某学生
的脚长为24厘米,据此估计其身高为
( )
A.160厘米
B.163厘米
C.166厘米
D.170厘米
C 由题意可知
=4x+
,又
=22.5,
=160,
因此160=22.5×4+
,解得
=70所以
=4x+70.
当x=24时,
=4×24+70=166.
13.(谢尔宾斯基地毯)如图,将一个正方形平均划分为9个小正方形,去掉中间的
小正方形,再对余下的小正方形重复这一操作,得到的图形称为“谢尔宾斯基地
毯”,在原正方形内部随机取一点,则该点取自“谢尔宾斯基地毯”的概率是
( )
A.
B.
C.
D.
A 设大正方形的边长为9,则每个小正方形的边长为1,则大正方形的面积为
9×9=81,则每个小正方形的面积为1,则所有阴影部分正方形的面积之和为
3×3+8=17,则剩余部分的面积为81-17=64,则对应概率P=
.
14.已知5件产品中有2件次品,其余为合格品.现从这5件产品中任取2件,恰有一件次品的概率为
( )
A.0.4
B.0.6
C.0.8
D.1
B 5件产品中有2件次品,记为a,b,有3件合格品,记为c,d,e,从这5件产品中任取
2件,有10种,分别是(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),
(c,e),(d,e),恰有一件次品,有6种,分别是(a,c),(a,d),(a,e),(b,c),
(b,d),(b,e),设事件A为“恰有一件次品”,则P(A)=
=0.6.
15.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如表:
则该营业窗口上午9点钟时,至少有1人排队的概率是________.?
排队人数
0
1
2
3
4
≥5
概率
0.1
0.16
0.3
0.3
0.1
0.04
【解析】由表格可得至少有1人排队的概率P=0.16+0.3+0.3+0.1+0.04=0.9.
答案:0.9
16.将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示,则7个剩余分数的中位数是________,方差是________.?
【解析】由题图可知去掉的两个数是87,99,所以
87+90×2+91×2+94+90+x=91×7,解得x=4,即7个数据是87,90,90,91,91,94,94,
故中位数是91,方差s2=
[(87-91)2+(90-91)2×2+(91-91)2×2+(94-91)2×2]
=
.
答案:91
统计与概率
真题再研析·提升审题力
考向一 统计
【典例】(2020·全国Ⅰ卷)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是
( )
A.y=a+bx
B.y=a+bx2
C.y=a+bex
D.y=a+bln
x
D 由散点图分布可知,散点图分布在一个对数函数的图象附近,因此,最适合作为发芽率y和温度x的回归方程类型的是y=a+bln
x.
考向二 概率
【典例】(2020·全国Ⅰ卷)设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为
( )
A 如图,从O,A,B,C,D
5个点中任取3个点有
{O,A,B},{O,A,C},{O,A,D},{O,B,C},
{O,B,D},{O,C,D},{A,B,C},{A,B,D},
{A,C,D},{B,C,D}共10种不同取法,
3点共线只有{O,A,C}与{O,B,D}共2种情况,
由古典概型的概率计算公式知,
取到3点共线的概率为
【考前必备】
1.线性回归分析的注意点
(1)回归直线一定过样本点的中心(
);
(2)已知样本点不一定在回归直线上;
(3)未知点的求解,通过代入回归直线方程求解即可.
2.独立性检验的注意点
K2的取值的意义有两种表述,当数值表中数值为0.01时,表述为失误率不超过1%的前提下,说两者相关;当数值表中数值为0.99时,表述为有99%的把握,说两者相关.
3.求较复杂的古典概型计算的两种方法
(1)树状图法:当事件个数没有很明显的规律,并且涉及的基本事件又不是太多时,我们可借助树状图法直观地将其表示出来.
(2)图表法:在求概率时,若事件可以表示成有序数对的形式,则可以把全体基本事件用平面直角坐标系中的点表示.
【考场秘技】
1.较复杂的事件的概率可灵活运用互斥事件、对立事件的概率公式简化运算.
2.频数、频率、样本容量的计算方法
(1)
×组距=频率;
(2)
=频率.
3.频率分布直方图中各小长方形的面积之和为1.
【命题陷阱】
1.求回归直线解析式时错用已知数据而不是
求解
【案例】T1要注意.先求出
=100,
=100,然后再求解a的值.
2.频率分布直方图中错把小长方形的高当成概率
【案例】T5求a的值,用概率之和为1的方法求解,应注意的是,每一个小长方形表
示的概率应该是
×组距.
1.对某同学7次考试的数学成绩x和物理成绩y进行分析,下面是该生7次考试的成绩.发现他的物理成绩y与数学成绩x是线性相关的,利用最小二乘法得到线性回归方程为y=0.5x+a,若该生的数学成绩达到130分,估计他的物理成绩大约是( )
A.114.5
B.115
C.115.5
D.116
高考演兵场·检验考试力
数学
88
83
117
92
108
100
112
物理
94
91
108
96
104
101
106
B 由题可知:
=100,
=100,所以a=
-0.5
=100-0.5×100=50,当x=130时,y=0.5×130+50=115.
2.已知两组数据x,y的对应关系如表所示,若根据表中的数据得出y关于x的线性回归方程为y=6.5x+17.5,则表中m的值为
( )
A.50
B.55
C.56.5
D.60
x
2
4
5
6
8
y
30
38
50
m
72
D 由表中数据,计算
=
×(2+4+5+6+8)=5,
=
×(30+38+50+m+72)=38+
,因为回归直线方程y=6.5x+17.5过样本点的
中心,所以38+
=6.5×5+17.5,解得m=60.
3.某班主任对班级51名同学进行了作业量多少的调查,结合数据建立了一个2×2
列联表,可能用到的公式:
可能用到的数据:
P
≈0.01,P
≈0.05,参照以上公式和数据,得到的正确结论
是( )
认为作业多
认为作业不多
总计
喜欢玩电
脑游戏
18
12
30
不喜欢玩
电脑游戏
5
16
21
总计
23
28
51
A.有95%的把握认为喜欢玩电脑游戏与认为作业多少有关
B.有95%的把握认为喜欢玩电脑游戏与认为作业多少无关
C.有99%的把握认为喜欢玩电脑游戏与认为作业多少有关
D.有99%的把握认为喜欢玩电脑游戏与认为作业多少无关
A 根据所给数据可得K2的观测值k=
≈6.535>3.841
,所以
有95%的把握认为喜欢玩电脑游戏与认为作业多少有关.
4.为了检验设备M与设备N的生产效率,研究人员作出统计,得到如表所示的结果,则
( )
设备M
设备N
生产出的合格产品
48
43
生产出的不合格产品
2
7
A.有90%的把握认为生产的产品质量与设备的选择具有相关性
B.没有90%的把握认为生产的产品质量与设备的选择具有相关性
C.可以在犯错误的概率不超过0.01的前提下认为生产的产品质量与设备的选择具有相关性
D.不能在犯错误的概率不超过0.01的前提下认为生产的产品质量与设备的选择具有相关性
A 将题表中的数据代入公式,计算得K2的观测值k=
≈3.053,
因为3.053>2.706,所以有90%的把握认为生产的产品质量与设备的选择具有相关
性.
5.某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1
120名学生中随机抽取了100
名学生的数学成绩,发现都在[80,150]内现将这100名学生的成绩按照
[80,90),[90,100),[100,110),[110,120),[120,130),
[130,140),[140,150]分组后,得到的频率
分布直方图如图所示,则下列说法正确的是
( )
A.频率分布直方图中a的值为
0.040
B.样本数据低于130分的频率为
0.3
C.总体的中位数(保留1位小数)估计为123.3分
D.总体分布在[90,100)的频数一定与总体分布在[100,110)的频数相等
C 由频率分布直方图得:(0.005+0.010+0.010+0.015+a+0.025+0.005)×10=1,
解得a=0.030,故A错误;样本数据低于130分的频率为:1-(0.025+0.005)×10=0.7,
故B错误;[80,120)的频率为:(0.005+0.010+0.010+0.015)×10=0.4,[120,130)
的频率为:0.030×10=0.3.
所以总体的中位数(保留1位小数)估计为:120+
×10≈123.3分,故C正确;
样本分布在[90,100)的频数一定与样本分布在[100,110)的频数相等,总体分布
在[90,100)的频数不一定与总体分布在[100,110)的频数相等,故D错误.
6.如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为
( )
C 从1,2,3,4,5中任取3个不同的数共有{1,2,3},
{1,2,4},{1,2,5},{1,3,4},
{1,3,5},{1,4,5},{2,3,4},{2,3,5},{2,4,5},{3,4,5}10种不同的取法.其中的
勾股数只有{3,4,5},故3个数构成一组勾股数的取法只有1种,故所求概率P=
.
7.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据环保部门某日早6点至晚9点在A县、B县两个地区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,A县、B县两个地区浓度的方差较小的是
( )
A.A县
B.B县
C.A县、B县两个地区相等
D.无法确定
A 根据茎叶图中的数据可知,A县的数据都集中在0.05和0.08之间,数据分布比较稳定,而B县的数据分布比较分散,不如A县数据集中,所以A县的方差较小.
8.
对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.用频率估计概率,现从该批产品中随机抽取一件,则其为二等品的概率为
( )
A.0.09
B.0.20
C.0.25
D.0.45
D 设区间[25,30)对应矩形的另一边长为x,由所有矩形面积之和为1,得(0.02+0.04+0.06+0.03+x)×5=1,解得x=0.05.产品为二等品的概率为0.04×5+0.05×5=0.45.
9.细木棒,长度分别为1,3,5,7,9(cm),从中任取三根,能搭成三角形的概率是
( )
D 设取出的三根木棒能搭成三角形为事件A,任取三根木棒按长度不同共有1、3、
5,1、3、7,1、3、9,1、5、7,1、5、9,1、7、9,3、5、7,3、5、9,3、7、9,5、
7、9,10种情况,由于三角形两边之和大于第三边,构成三角形的只有3、5、7,3、
7、9,5、7、9三种情况,故所求概率为P(A)=
.
10.甲、乙两人参加普法知识竞赛,共有5道不同的题目,其中选择题3道,填空题2道.甲、乙两人依次抽取1道题,则甲抽中选择题、乙抽中填空题的概率等于( )
10.C 记选择题为A,B,C,填空题为d,e.
则甲、乙两人依次抽取,不同的结果有:
(A,B),(A,C),(A,d),(A,e),
(B,A),(B,C),(B,d),(B,e),
(C,A),(C,B),(C,d),(C,e),
(d,A),(d,B),(d,C),(d,e),
(e,A),(e,B),(e,C),(e,d).
共20个.
其中甲抽中选择题、乙抽中填空题的结果有:
(A,d),(A,e),(B,d),(B,e),(C,d),(C,e),共6个.
所以甲抽中选择题、乙抽中填空题的概率P=
11.山东电视台“国学小名士”的播出引发了学校的国学热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“国学达人”的称号,小于85分且不小于70分的学生得到“国学能手”的称号,其他学生得到“国学爱好者”的称号,根据该次比赛的成绩按照称号的不同进行分层抽样,抽选10名学生,则抽选的学生中获得“国学达人”称号的人数为
( )
A.2
B.4
C.5
D.6
A 由茎叶图可得,获“国学达人”称号的有8人,据该次比赛的成绩按照称号的
不同进行分层抽样,抽选10名学生,则抽选的学生中获得“国学达人”称号的人
数为8×
=2.
12.为了研究某班学生的脚长x(单位:厘米)和身高y(单位:厘米)的关系,从该班
随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,
设其回归直线方程为
,已知
=225,
=1
600,
=4.该班某学生
的脚长为24厘米,据此估计其身高为
( )
A.160厘米
B.163厘米
C.166厘米
D.170厘米
C 由题意可知
=4x+
,又
=22.5,
=160,
因此160=22.5×4+
,解得
=70所以
=4x+70.
当x=24时,
=4×24+70=166.
13.(谢尔宾斯基地毯)如图,将一个正方形平均划分为9个小正方形,去掉中间的
小正方形,再对余下的小正方形重复这一操作,得到的图形称为“谢尔宾斯基地
毯”,在原正方形内部随机取一点,则该点取自“谢尔宾斯基地毯”的概率是
( )
A.
B.
C.
D.
A 设大正方形的边长为9,则每个小正方形的边长为1,则大正方形的面积为
9×9=81,则每个小正方形的面积为1,则所有阴影部分正方形的面积之和为
3×3+8=17,则剩余部分的面积为81-17=64,则对应概率P=
.
14.已知5件产品中有2件次品,其余为合格品.现从这5件产品中任取2件,恰有一件次品的概率为
( )
A.0.4
B.0.6
C.0.8
D.1
B 5件产品中有2件次品,记为a,b,有3件合格品,记为c,d,e,从这5件产品中任取
2件,有10种,分别是(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),
(c,e),(d,e),恰有一件次品,有6种,分别是(a,c),(a,d),(a,e),(b,c),
(b,d),(b,e),设事件A为“恰有一件次品”,则P(A)=
=0.6.
15.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如表:
则该营业窗口上午9点钟时,至少有1人排队的概率是________.?
排队人数
0
1
2
3
4
≥5
概率
0.1
0.16
0.3
0.3
0.1
0.04
【解析】由表格可得至少有1人排队的概率P=0.16+0.3+0.3+0.1+0.04=0.9.
答案:0.9
16.将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示,则7个剩余分数的中位数是________,方差是________.?
【解析】由题图可知去掉的两个数是87,99,所以
87+90×2+91×2+94+90+x=91×7,解得x=4,即7个数据是87,90,90,91,91,94,94,
故中位数是91,方差s2=
[(87-91)2+(90-91)2×2+(91-91)2×2+(94-91)2×2]
=
.
答案:91
同课章节目录
