直线与平面的位置关系课件(共23张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 直线与平面的位置关系课件(共23张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 416.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 21:38:21 | ||
图片预览






文档简介
(共23张PPT)
直线与平面的位置关系
真题再研析·提升审题力
考向一 直线与平面的位置关系
【典例】(2020·全国Ⅱ卷)设有下列四个命题:
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l?平面α,直线m⊥平面α,则m⊥l.
则下述命题中所有真命题的序号是__________.?
①p1∧p4
②p1∧p2
③?
p2∨p3
④?
p3∨?p4
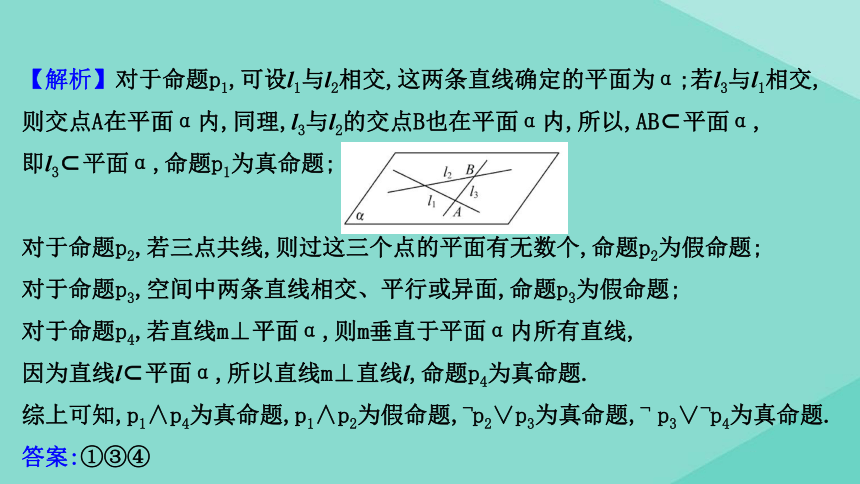
【解析】对于命题p1,可设l1与l2相交,这两条直线确定的平面为α;若l3与l1相交,则交点A在平面α内,同理,l3与l2的交点B也在平面α内,所以,AB?平面α,
即l3?平面α,命题p1为真命题;
对于命题p2,若三点共线,则过这三个点的平面有无数个,命题p2为假命题;
对于命题p3,空间中两条直线相交、平行或异面,命题p3为假命题;
对于命题p4,若直线m⊥平面α,则m垂直于平面α内所有直线,
因为直线l?平面α,所以直线m⊥直线l,命题p4为真命题.
综上可知,p1∧p4为真命题,p1∧p2为假命题,?p2∨p3为真命题,?
p3∨?p4为真命题.
答案:①③④
考向二 空间中垂直关系
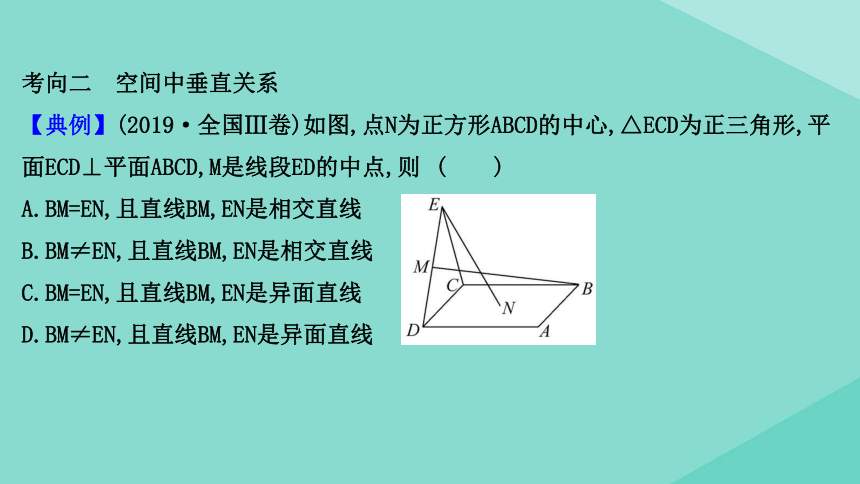
【典例】(2019·全国Ⅲ卷)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则
( )
A.BM=EN,且直线BM,EN是相交直线
B.BM≠EN,且直线BM,EN是相交直线
C.BM=EN,且直线BM,EN是异面直线
D.BM≠EN,且直线BM,EN是异面直线
B 因为直线BM,EN都是平面BED内的直线,且不平行,
即直线BM,EN是相交直线.设正方形ABCD的边长为2a,
则由题意可得:DE=2a,DM=a,DN=
a,DB=2
a,
根据余弦定理可得:BM2=DB2+DM2-2DB·DMcos∠BDE=9a2-4
a2cos∠BDE,
EN2=DE2+DN2-2DE·DNcos∠BDE=6a2-4
a2cos∠BDE,
所以BM≠EN.
【考前必备】
1.证明线面平行与线线平行
(1)证明线面平行,通常用判定定理:
因为l∥a,a?α,l?α,所以l∥α.
(2)证明线线平行,通常用性质定理:
因为l∥α,l?β,α∩β=b,所以l∥b,关键是找到与α相交且包含l的平面β.
2.证明线面垂直的思维流程
(1)找相交直线:在一个平面内找到两条相交直线;
(2)证线线垂直:证明平面外的直线与这两条相交直线都垂直;
(3)证线面垂直:利用直线与平面垂直的判定定理证得线面垂直.
【考场秘技】
1.异面直线的判定方法
平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线.
2.异面直线所成角的求法
通过平移直线,把异面问题转化为相交直线的夹角,一般有3种类型:
(1)利用图形中已有的平行线平移;
(2)利用特殊点(线段的端点或中点)作平行线平移;
(3)补形平移.计算异面直线所成的角通常放在三角形中进行.
3.证明线面平行的常用方法
(1)构造平行四边形,证得线线平行,进而证得线面平行.
(2)构造三角形中位线,证得线线平行,进而证得线面平行.
(3)在同一个面中找到两条平行直线,证得线线平行,进而证得线面平行.
【命题陷阱】
1.判断直线与平面的位置关系时,容易考虑不全面.
【案例】T3若m∥α,n∥α,则m与n可以平行、相交、异面,故①错误.
2.容易忽略线在面内的情况.
【案例】T2在A中,若a⊥b,a⊥α,则b∥α或b?α,故A错误.
3.通过平移异面直线构成三角形求异面直线所成角时,容易忽略补角的情况.
【案例】T4①构成三角形后.若通过解三角形得到内角的余弦值为负值时,要取补角.
1.如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=AB=2,∠BAD=60°,M是BB1的中点,则异面直线A1M与B1C所成角的余弦值为
( )
A.-
B.-
C.
D.
高考演兵场·检验考试力
D 由题意可得
2.设a,b是不同的直线,α,β是不同的平面,则下列四个命题中正确的是
( )
A.若a⊥b,a⊥α,则b∥α
B.若a∥α,α⊥β,则a⊥β
C.若a⊥β,α⊥β,则a∥α
D.若a⊥b,a⊥α,b⊥β,则α⊥β
D 由a,b是两条不同的直线,α,β是两个不同的平面,
得:在A中,若a⊥b,a⊥α,则b∥α或b?α,故A错误;
在B中,若a∥α,β⊥α,则a也可能在β内,故B错误;
在C中,若a⊥β,α⊥β,则a∥α或a?α,故C错误;
在D中,若a⊥b,a⊥α,b⊥β,则β⊥α成立,故D正确.
3.已知m,n是两条不同的直线,α,β是两个不同的平面,有下列四个命题:
①若m∥α,n∥α,则m∥n;
②若n⊥α,m⊥β,m∥n,则α∥β;
③若α⊥β,m∥α,n⊥β,则m∥n;
④若α∥β,m?α,m⊥n,则n⊥β.
其中,正确的命题个数是
( )
A.3
B.2
C.1
D.0
C 若m∥α,n∥α,则m与n可以平行、相交、异面,故①错误;
若n⊥α,m⊥β,m∥n,则α∥β,故②正确;
若α⊥β,m∥α,n⊥β,则m与n可以平行、相交、异面,故③错误;
若α∥β,m?α,m⊥n,则n与β可以平行、相交或n?β,故④错误,
所以正确的命题个数是1.
4.如图,在正三棱柱ABC-A1B1C1中底面边长、侧棱长都是4,E,F分别是A1C1,BC的
中点,则以下四个结论中正确的是
( )
①AE与C1F所成的角的余弦值为
;
②C1F平行于平面ABE;
③三棱锥E-ABC的体积为
;
④AB垂直于EC.
A.①②③
B.②③④
C.①③④
D.①②④
A 取AC的中点G,连接GC1,GF,
则AE平行于GC1.在三角形GFC1中,GC1=FC1=
.
由余弦定理得cos∠GC1F=
,所以①正确.
取AB的中点H,连接EH,FH,则EC1平行且等于HF,
所以四边形HFC1E为平行四边形,所以C1F∥EH,
又C1F不在平面ABE内,EH?平面ABE,所以C1F∥平面ABE,
所以②正确.
三棱锥E-ABC的体积
所以③正确.
假设AB垂直于EC,
又因为AB垂直于A1A,EC,AA1都在平面ACC1A1内且EC与AA1相交,
所以AB垂直于侧面ACC1A1,所以AB垂直于AC,这与∠BAC等于60°矛盾,
所以④错误.
5.如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则F在侧面CDD1C1上的轨迹的长度是
( )
A.a
B.
C.
a
D.
D 设G,H,I分别为CD,CC1,C1D1边上的中点,
则A1,B,E,G四点共面,且平面A1BGE∥平面B1HI,
又因为B1F∥平面A1BE,所以F落在线段HI上,
因为正方体ABCD-A1B1C1D1中的棱长为a,
所以HI=
CD1=
a,
即F在侧面CDD1C1上的轨迹的长度是
a.
6.如图,PA垂直于以AB为直径的圆所在平面,C为圆上异于A,B的任意一点,AE⊥PC垂足为E,点F是PB上一点,则下列判断中不正确的是
( )
A.BC⊥平面PAC
B.AE⊥EF
C.AC⊥PB
D.平面AEF⊥平面PBC
C 对于A,PA垂直于以AB为直径的圆所在平面,
而BC在底面圆面内,则PA⊥BC,
又由圆的性质可知AC⊥BC,且PA∩AC=A,
则BC⊥平面PAC,所以A正确;
对于B,由A可知BC⊥AE,由题意可知AE⊥PC,且BC∩PC=C,
所以AE⊥平面PCB,而EF?平面PCB,所以AE⊥EF,所以B正确;
对于C,由B可知AE⊥平面PCB,因而AC与平面PCB不垂直,
所以AC⊥PB不成立,所以C错误.
对于D,由A,B可知,BC⊥平面PAC,BC?平面PCB,
由面面垂直的性质可得平面AEF⊥平面PBC.所以D正确;
直线与平面的位置关系
真题再研析·提升审题力
考向一 直线与平面的位置关系
【典例】(2020·全国Ⅱ卷)设有下列四个命题:
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l?平面α,直线m⊥平面α,则m⊥l.
则下述命题中所有真命题的序号是__________.?
①p1∧p4
②p1∧p2
③?
p2∨p3
④?
p3∨?p4
【解析】对于命题p1,可设l1与l2相交,这两条直线确定的平面为α;若l3与l1相交,则交点A在平面α内,同理,l3与l2的交点B也在平面α内,所以,AB?平面α,
即l3?平面α,命题p1为真命题;
对于命题p2,若三点共线,则过这三个点的平面有无数个,命题p2为假命题;
对于命题p3,空间中两条直线相交、平行或异面,命题p3为假命题;
对于命题p4,若直线m⊥平面α,则m垂直于平面α内所有直线,
因为直线l?平面α,所以直线m⊥直线l,命题p4为真命题.
综上可知,p1∧p4为真命题,p1∧p2为假命题,?p2∨p3为真命题,?
p3∨?p4为真命题.
答案:①③④
考向二 空间中垂直关系
【典例】(2019·全国Ⅲ卷)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则
( )
A.BM=EN,且直线BM,EN是相交直线
B.BM≠EN,且直线BM,EN是相交直线
C.BM=EN,且直线BM,EN是异面直线
D.BM≠EN,且直线BM,EN是异面直线
B 因为直线BM,EN都是平面BED内的直线,且不平行,
即直线BM,EN是相交直线.设正方形ABCD的边长为2a,
则由题意可得:DE=2a,DM=a,DN=
a,DB=2
a,
根据余弦定理可得:BM2=DB2+DM2-2DB·DMcos∠BDE=9a2-4
a2cos∠BDE,
EN2=DE2+DN2-2DE·DNcos∠BDE=6a2-4
a2cos∠BDE,
所以BM≠EN.
【考前必备】
1.证明线面平行与线线平行
(1)证明线面平行,通常用判定定理:
因为l∥a,a?α,l?α,所以l∥α.
(2)证明线线平行,通常用性质定理:
因为l∥α,l?β,α∩β=b,所以l∥b,关键是找到与α相交且包含l的平面β.
2.证明线面垂直的思维流程
(1)找相交直线:在一个平面内找到两条相交直线;
(2)证线线垂直:证明平面外的直线与这两条相交直线都垂直;
(3)证线面垂直:利用直线与平面垂直的判定定理证得线面垂直.
【考场秘技】
1.异面直线的判定方法
平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线.
2.异面直线所成角的求法
通过平移直线,把异面问题转化为相交直线的夹角,一般有3种类型:
(1)利用图形中已有的平行线平移;
(2)利用特殊点(线段的端点或中点)作平行线平移;
(3)补形平移.计算异面直线所成的角通常放在三角形中进行.
3.证明线面平行的常用方法
(1)构造平行四边形,证得线线平行,进而证得线面平行.
(2)构造三角形中位线,证得线线平行,进而证得线面平行.
(3)在同一个面中找到两条平行直线,证得线线平行,进而证得线面平行.
【命题陷阱】
1.判断直线与平面的位置关系时,容易考虑不全面.
【案例】T3若m∥α,n∥α,则m与n可以平行、相交、异面,故①错误.
2.容易忽略线在面内的情况.
【案例】T2在A中,若a⊥b,a⊥α,则b∥α或b?α,故A错误.
3.通过平移异面直线构成三角形求异面直线所成角时,容易忽略补角的情况.
【案例】T4①构成三角形后.若通过解三角形得到内角的余弦值为负值时,要取补角.
1.如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=AB=2,∠BAD=60°,M是BB1的中点,则异面直线A1M与B1C所成角的余弦值为
( )
A.-
B.-
C.
D.
高考演兵场·检验考试力
D 由题意可得
2.设a,b是不同的直线,α,β是不同的平面,则下列四个命题中正确的是
( )
A.若a⊥b,a⊥α,则b∥α
B.若a∥α,α⊥β,则a⊥β
C.若a⊥β,α⊥β,则a∥α
D.若a⊥b,a⊥α,b⊥β,则α⊥β
D 由a,b是两条不同的直线,α,β是两个不同的平面,
得:在A中,若a⊥b,a⊥α,则b∥α或b?α,故A错误;
在B中,若a∥α,β⊥α,则a也可能在β内,故B错误;
在C中,若a⊥β,α⊥β,则a∥α或a?α,故C错误;
在D中,若a⊥b,a⊥α,b⊥β,则β⊥α成立,故D正确.
3.已知m,n是两条不同的直线,α,β是两个不同的平面,有下列四个命题:
①若m∥α,n∥α,则m∥n;
②若n⊥α,m⊥β,m∥n,则α∥β;
③若α⊥β,m∥α,n⊥β,则m∥n;
④若α∥β,m?α,m⊥n,则n⊥β.
其中,正确的命题个数是
( )
A.3
B.2
C.1
D.0
C 若m∥α,n∥α,则m与n可以平行、相交、异面,故①错误;
若n⊥α,m⊥β,m∥n,则α∥β,故②正确;
若α⊥β,m∥α,n⊥β,则m与n可以平行、相交、异面,故③错误;
若α∥β,m?α,m⊥n,则n与β可以平行、相交或n?β,故④错误,
所以正确的命题个数是1.
4.如图,在正三棱柱ABC-A1B1C1中底面边长、侧棱长都是4,E,F分别是A1C1,BC的
中点,则以下四个结论中正确的是
( )
①AE与C1F所成的角的余弦值为
;
②C1F平行于平面ABE;
③三棱锥E-ABC的体积为
;
④AB垂直于EC.
A.①②③
B.②③④
C.①③④
D.①②④
A 取AC的中点G,连接GC1,GF,
则AE平行于GC1.在三角形GFC1中,GC1=FC1=
.
由余弦定理得cos∠GC1F=
,所以①正确.
取AB的中点H,连接EH,FH,则EC1平行且等于HF,
所以四边形HFC1E为平行四边形,所以C1F∥EH,
又C1F不在平面ABE内,EH?平面ABE,所以C1F∥平面ABE,
所以②正确.
三棱锥E-ABC的体积
所以③正确.
假设AB垂直于EC,
又因为AB垂直于A1A,EC,AA1都在平面ACC1A1内且EC与AA1相交,
所以AB垂直于侧面ACC1A1,所以AB垂直于AC,这与∠BAC等于60°矛盾,
所以④错误.
5.如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则F在侧面CDD1C1上的轨迹的长度是
( )
A.a
B.
C.
a
D.
D 设G,H,I分别为CD,CC1,C1D1边上的中点,
则A1,B,E,G四点共面,且平面A1BGE∥平面B1HI,
又因为B1F∥平面A1BE,所以F落在线段HI上,
因为正方体ABCD-A1B1C1D1中的棱长为a,
所以HI=
CD1=
a,
即F在侧面CDD1C1上的轨迹的长度是
a.
6.如图,PA垂直于以AB为直径的圆所在平面,C为圆上异于A,B的任意一点,AE⊥PC垂足为E,点F是PB上一点,则下列判断中不正确的是
( )
A.BC⊥平面PAC
B.AE⊥EF
C.AC⊥PB
D.平面AEF⊥平面PBC
C 对于A,PA垂直于以AB为直径的圆所在平面,
而BC在底面圆面内,则PA⊥BC,
又由圆的性质可知AC⊥BC,且PA∩AC=A,
则BC⊥平面PAC,所以A正确;
对于B,由A可知BC⊥AE,由题意可知AE⊥PC,且BC∩PC=C,
所以AE⊥平面PCB,而EF?平面PCB,所以AE⊥EF,所以B正确;
对于C,由B可知AE⊥平面PCB,因而AC与平面PCB不垂直,
所以AC⊥PB不成立,所以C错误.
对于D,由A,B可知,BC⊥平面PAC,BC?平面PCB,
由面面垂直的性质可得平面AEF⊥平面PBC.所以D正确;
同课章节目录
