统计与统计案例的交汇 课件(共53张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 统计与统计案例的交汇 课件(共53张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 631.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 21:38:48 | ||
图片预览











文档简介
(共53张PPT)
统计与统计案例的交汇
真题再研析·提升审题力
【典例】(12分)(2020·全国Ⅱ卷)某沙漠地区经过治理,生态系统得到很大改善,
野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近
的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到
样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积
(单位:公顷)和这种野生动物的数量,并计算得
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区
这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以
获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方
法,并说明理由.
附:相关系数
【审题·逆向思维】
(1)该地区这种野生动物数量的估计值?样区这种野生动物数量的平均数乘以地块数;
(2)样本相关系数?相关系数公式;
(3)分层抽样方法?提高样本数据的代表性?各地块间植物覆盖面积差异较大.
【标准答案】(1)样区这种野生动物数量的平均数
为
……………………2分
地块数为200,该地区这种野生动物数量的估计值为200×60=12
000.
……………………4分
(2)样本(xi,yi)(i=1,2,…,20)的相关系数为
……………………8分
(3)分层抽样:根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽样,理由如下:
由(2)知各地块的这种野生动物的数量与植物覆盖面积有很强的正相关,由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物的数量差异也很大,采用分层抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本代表性,从而可以获得该地区这种野生动物数量更准确的估计.…………12分
【深度解读】
测试
目标
(1)直接运用公式解决问题;
(2)直接运用相关系数公式解题;
(3)通过对分层抽样的理解选择合适的抽样方法.
测试
目标
逻辑推理:根据不同地块的物种差异较大特征选择抽样方法;
数据分析:通过平均数求得野生动物数量的估计值;
数学运算:运用公式求解相关系数.
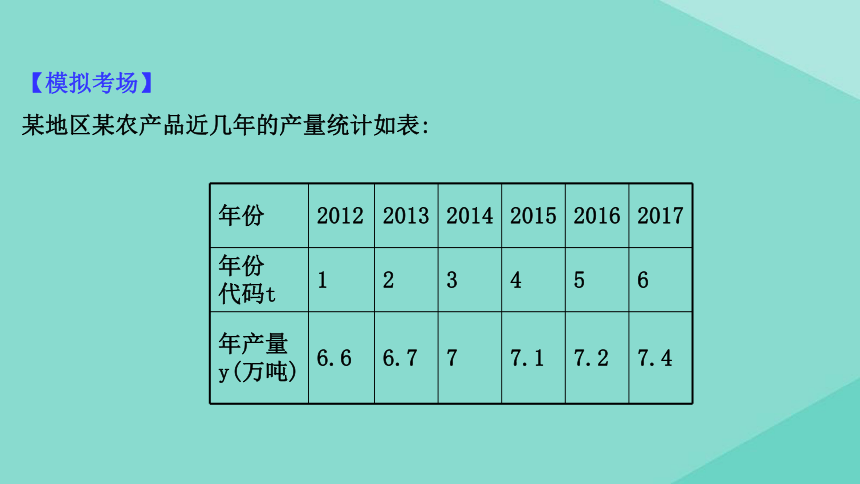
【模拟考场】
某地区某农产品近几年的产量统计如表:
年份
2012
2013
2014
2015
2016
2017
年份
代码t
1
2
3
4
5
6
年产量
y(万吨)
6.6
6.7
7
7.1
7.2
7.4
(1)根据表中数据,建立关于t的线性回归方程
;
(2)根据线性回归方程预测2019年该地区该农产品的年产量.
(参考数据:
计算结果保留小数点后两位)
【解析】(1)由题意可知:
+0.52+1.52+2.52=17.5,所以
=0.16,
又
=7-0.16×3.5=6.44,
所以y关于t的线性回归方程为
=0.16t+6.44.
(2)由(1)可得,当年份为2019年时,年份代码t=8,
此时
=0.16×8+6.44=7.72,所以,可预测2019年该地区该农产品的年产量
约为7.72万吨.
【考场秘技】
1.求线性回归方程的关键是确定回归系数
,应充分利用回归直线过样本点中
心
,而所有样本点可能都不在直线上.
2.根据线性回归方程计算的
值,仅是一个预报值,而不是真实发生的值.
3.求线性回归方程的关键
(1)正确理解计算
的公式和准确计算.
(2)在分析两个变量的相关关系时,可根据样本数据作出散点图来确定两个变量
之间是否具有相关关系,若具有线性相关关系,则可通过线性回归方程估计和预
测变量的值.
4.独立性检验的关键
(1)根据2×2列联表准确计算K2的观测值k,若2×2列联表没有列出来,要先列出此表.
(2)K2的观测值k越大,则两类分类变量有关的把握越大,犯错的概率越小.
【万能模板】
独立性验证的步骤:
(1)列出2×2列联表:注意求出各行各列的总值,方便计算;
(2)将表中数据代入K2公式,计算出K2的观测值k;
(3)根据k的值参考表格,求出相关的概率;
(4)下结论.
【阅卷点评】
1.步骤分:(1)相关性系数公式;(2)K2公式.
2.关键分:解题过程的关键点,有则给分,无则没分.如选择分层抽样的依据为各个地块物种数量差异性很大.
3.计算分:用平均值估计这种野生动物数量的总值,相关系数的求解.
4.注意区分分层抽样与简单随机抽样,如:(1)整体分成了有明显差异的几部分,要选择分层抽样,(2)如果个体的差异不明显,可以选择简单随机抽样.
1.(独立性检验)在新冠肺炎疫情期间,为了指导不同人群科学合理地选择和使用
口罩,现对N95口罩的了解情况进行调查.现随机抽取40人进行调查,其中45岁以
下的有20人.在接受调查的40人中,对于N95这种口罩了解的占50%,在了解的人中
45岁以上(含45岁)的人数占
.
(1)将列联表补充完整;
高考演兵场·检验考试力
了解
不了解
总计
45岁以下
45岁以上(含45岁)
总计
40
(2)判断是否有99%的把握认为对N95这种口罩的了解与否与年龄有关.
参考公式:K2=
,其中n=a+b+c+d.
参考数据:
P(K2≥k0)
0.10
0.05
0.010
0.001
k0
2.706
3.841
6.635
10.828
1.【解析】(1)由题意可得对于N95这种口罩了解的人数为40×50%=20,则45岁以
上(含45岁)的人对N95这种口罩了解的人数为20×
=5.故补充列联表如下:
了解
不了解
总计
45岁以下
15
5
20
45岁以上(含45岁)
5
15
20
总计
20
20
40
(2)由题意可得,K2的观测值k=
=10,
因为10>6.635,所以有99%的把握认为对N95这种口罩的了解与否与年龄有关.
2.(回归分析)随着智能手机的普及,使用手机上网成为人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价x(单位:元/月)和购买人数y(单位:万人)的关系如表:
流量包的定
价x(元/月)
30
35
40
45
50
购买人数y(万人)
18
14
10
8
5
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟
合y与x的关系?并指出是正相关还是负相关;
(2)①求出y关于x的回归方程;
②若该通信公司在一个类似于试点的城市中将这款流量包的价格定为25元/月,
请用所求回归方程预测该市一个月内购买该流量包的人数能否超过20万人.
参考数据:
2.【解析】(1)根据题意,得
可列表如下
根据表格和参考数据,得
因而相关系数
由于
≈0.99,很接近1,因而可以用线性回归方程模型拟合y与x的关系.
由于r<0,故其关系为负相关.
(2)①
=11+0.64×40=36.6,
因而y关于x的回归方程为
=-0.64x+36.6.
②由①知,若x=25,则
=-0.64×25+36.6=20.6>20,故若将流量包的价格定为
25元/月,可预测该市一个月内购买该流量包的人数会超过20万人.
3.(独立性检验)2019年12月1日起郑州市施行《郑州市城市生活垃圾分类管理办法》,郑州正式进入城市生活垃圾分类时代.为了增强社区居民对垃圾分类知识的了解,积极参与到垃圾分类的行动中,某社区采用线下和线上相结合的方式开展了一次200名辖区成员参加的“垃圾分类有关知识”专题培训.为了了解参训成员对于线上培训、线下培训的满意程度,社区居委会随机选取了40名辖区成员,将他们分成两组,每组20人,分别对线上、线下两种培训进行满意度测评,根据辖区成员的评分(满分100分)绘制了如图所示的茎叶图.
(1)根据茎叶图判断辖区成员对于线上、线下哪种培训的满意度更高,并说明理由.
(2)求这40名辖区成员满意度评分的中位数m,并将评分不超过m、超过m分别视为“基本满意”“非常满意”两个等级.
(ⅰ)利用样本估计总体的思想,估算本次培训共有多少辖区成员对线上培训非常满意;
(ⅱ)根据茎叶图填写下面的列联表.
基本满意
非常满意
总计
线上培训
线下培训
总计
并根据列联表判断能否有99.5%的把握认为辖区成员对两种培训方式的满意度有差异?
3.【解析】(1)由茎叶图可知,线上培训的满意度评分在茎7上的最多,关于茎7大
致呈对称分布,线下培训的满意度评分分布在茎8上的最多,关于茎8大致呈对称
分布,故可以认为线下培训满意度评分比线上培训满意度评分更高,因此辖区成
员对线下培训的满意度更高.
(2)由茎叶图知m=
=80.
(ⅰ)参加线上培训满意度调查的20名辖区成员中共有6名成员对线上培训非常满
意,频率为
,又本次培训共200名成员参加,所以对线上培训非常满意的成员约
有200×
=60(人).
(ⅱ)列联表如下:
基本满意
非常满意
总计
线上培训
14
6
20
线下培训
6
14
20
总计
20
20
40
于是K2的观测值k=
=6.4,由于6.4<7.879,
所以没有99.5%的把握认为辖区成员对两种培训方式的满意度有差异.
4.(独立性检验)2020年3月,因为新冠肺炎疫情的影响,我市全体学生只能在网上在线学习,为了研究学生在线学习情况,市教研院数学学科随机从市区各高中学校抽取120名学生对线上教学情况进行调查(其中,男生与女生的人数之比为3∶1),结果发现:男生中有40名对于线上教学满意,女生中有10名表示对于线上教学不满意.
(1)请完成如表2×2列联表,并回答能否有95%的把握认为“对线上教学是否满意与性别有关”;
态度性别
满意
不满意
总计
男生
女生
总计
120
(2)采用分层抽样的方法,从被调查的对线上教学满意的学生中,抽取6名学生,再从这6名学生中抽取2名学生,作线上学习的经验介绍,求所选取的2名学生性别不同的概率.
4.【解析】(1)由题意可知抽取的120名学生中男生有90人,女生有30人,则列联
表如下:
K2的观测值k=
≈4.4>3.841,则有95%的把握认为“对线上教
学是否满意与性别有关”.
态度性别
满意
不满意
总计
男生
40
50
90
女生
20
10
30
总计
60
60
120
(2)由分层抽样的性质可知,抽取的6名学生中,男生4人,女生2人,
记4名男生分别为a,b,c,d,2名女生分别为A,B,
从这6名学生中抽取2名学生的所有情况为:
,{c,d},{c,A},{c,B},
{d,A},{d,B},{A,B},共15种,
其中所选取的2名学生性别不同的共有8种,
则所选取的2名学生性别不同的概率P=
.
5.(回归分析)某电子科技公司由于产品采用最新技术,销售额不断增长,最近5个季度的销售额数据统计如下表(其中2018Q1表示2018年第一季度,以此类推):
季度
2018Q1
2018Q2
2018Q3
2018Q4
2019Q1
季度编号x
1
2
3
4
5
销售额y(百万元)
46
56
67
86
96
(1)公司市场部从中任选2个季度的数据进行对比分析,求这2个季度的销售额
都超过6千万元的概率;
(2)求y关于x的线性回归方程,并预测该公司2019Q3的销售额.
附:线性回归方程
.
参考数据:
=1
183.
5.【解析】(1)从5个季度的数据中任选2个,这2个季度的销售额有10种情况:(46,56),(46,67),(46,86),(46,96),(56,67),(56,86),(56,96),(67,86),
(67,96),(86,96).
设“这2个季度的销售额都超过6千万元”为事件A,事件A包含(67,86),(67,96),
(86,96),共3种情况.
所以P(A)=
.
(2)
(1+2+3+4+5)=3,
(46+56+67+86+96)=70.2.
所以
=31.2.
所以y关于x的线性回归方程为
=13x+31.2.令x=7,
得
=13×7+31.2=122.2(百万元).
所以预测该公司2019Q3的销售额为122.2百万元.
6.(独立性检验)今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严
控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员100人,其中50岁
及以上的共有40人.这100人中确诊的有10名,其中50岁以下的人占
.
确诊患新冠肺炎
未确诊患新冠肺炎
总计
50岁及以上
40
50岁以下
总计
10
100
(1)请将列联表补充完整,并判断是否有95%的把握认为是否确诊患新冠肺炎与年龄有关;
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,若从这5人中随机抽取3人,求恰有2人为50岁及以上的概率.
6.【解析】(1)因为100人中确诊的有10名,其中50岁以下的人占
,
所以50岁以下的确诊人数为4,50岁及以上的确诊人数为6.
因为50岁及以上的共有40人,
列联表补充如下,
确诊患新
冠肺炎
未确诊患
新冠肺炎
总计
50岁及
以上
6
34
40
50岁
以下
4
56
60
总计
10
90
100
则K2的观测值k=
≈1.852<3.841,所以没有95%的把握认为是
否确诊患新冠肺炎与年龄有关.
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,则抽取的5人中,有3人
50岁及以上,分别记作a,b,c;2人50岁以下,记作d,e.从中任取3人,可能的不同结
果有:
abc,abd,abe;acd,ace;ade;bcd,bce;bde;cde,共10种不同的情况,
恰有两人为50岁及以上的情况有abd,abe,acd,ace,bcd,bce,共6种不同的情况,
由于每种情况都是等可能的,所以恰有2人为50岁及以上的概率为
.
7.(回归分析)某单位响应党中央“精准扶贫”号召,对某村6户贫困户中的甲户进行定点帮扶,每年跟踪调查统计一次,从2015年1月1日至2018年12月底统计数据如下(人均年纯收入):
年份
2015年
2016年
2017年
2018年
年份代码x
1
2
3
4
收入y(百元)
25
28
32
35
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均
年纯收入为3
747元)
(2)2019年初,根据扶贫办的统计知,该村剩余5户贫困户中还有2户没有脱贫,
现从这5户中抽取2户,求至少有一户没有脱贫的概率.
7.【解析】(1)根据表格中数据可得,
=30,
xiyi=1×25+2×28+3×32+4×35=317,
=12+22+32+42=30,
所以
所以y关于x的线性回归方程是
=3.4x+21.5,当x=5时,
=38.5(百元),
因为3
850>3
747,所以甲户在2019年能够脱贫.
(2)设没有脱贫的2户为A,B,另3户为C,D,E,所有可能的情况
为:AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共有10种.其中至少有一户没有脱贫的情
况有7种.所以至少有一户没有脱贫的概率为
.
8.(独立性检验)2011年,国际数学协会正式宣布,将每年的3月14日设为国际数学
节,来源是中国古代数学家祖冲之的圆周率,为庆祝该节日,某校举办数学趣味知
识竞赛活动,参与竞赛的文科生与理科生人数之比为1∶3,且成绩分布在
,
分数在
分别获二等奖和一等奖.按文理科用分层抽样的方法抽取
200人的成绩作为样本,得到成绩的频率分布直方图.
(1)填写下面的2×2列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
文科生
理科生
总计
获奖
5
不获奖
总计
200
(2)将上述调查所得的频率视为概率,现从参赛学生中,通过分层抽样的方法从这些获奖人中随机抽取4人,再从这4人中任意选取2人,求2人均获二等奖的概率.
8.【解析】(1)补全2×2列联表如下.
K2的观测值k=
≈4.167>3.841.所以有超过95%的把握认为
“获奖与学生的文理科有关”.
文科生
理科生
总计
获奖
5
35
40
不获奖
45
115
160
总计
50
150
200
(2)由已知可得,分数在[80,90)获二等奖的参赛学生中抽取3人,分数
在[90,100]获一等奖的参赛学生中抽取1人.
记获二等奖的3人分别为a,b,c,获一等奖的1人为A,事件E为“从这4人中抽取2人
且这2人均获二等奖”.
从这4人中随机抽取2人的基本事件为
共6种,
其中2人均获二等奖的情况有
共3种,由古典概型的概率计算公式
得P
.
故2人均获二等奖的概率为
.
统计与统计案例的交汇
真题再研析·提升审题力
【典例】(12分)(2020·全国Ⅱ卷)某沙漠地区经过治理,生态系统得到很大改善,
野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近
的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到
样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积
(单位:公顷)和这种野生动物的数量,并计算得
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区
这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以
获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方
法,并说明理由.
附:相关系数
【审题·逆向思维】
(1)该地区这种野生动物数量的估计值?样区这种野生动物数量的平均数乘以地块数;
(2)样本相关系数?相关系数公式;
(3)分层抽样方法?提高样本数据的代表性?各地块间植物覆盖面积差异较大.
【标准答案】(1)样区这种野生动物数量的平均数
为
……………………2分
地块数为200,该地区这种野生动物数量的估计值为200×60=12
000.
……………………4分
(2)样本(xi,yi)(i=1,2,…,20)的相关系数为
……………………8分
(3)分层抽样:根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽样,理由如下:
由(2)知各地块的这种野生动物的数量与植物覆盖面积有很强的正相关,由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物的数量差异也很大,采用分层抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本代表性,从而可以获得该地区这种野生动物数量更准确的估计.…………12分
【深度解读】
测试
目标
(1)直接运用公式解决问题;
(2)直接运用相关系数公式解题;
(3)通过对分层抽样的理解选择合适的抽样方法.
测试
目标
逻辑推理:根据不同地块的物种差异较大特征选择抽样方法;
数据分析:通过平均数求得野生动物数量的估计值;
数学运算:运用公式求解相关系数.
【模拟考场】
某地区某农产品近几年的产量统计如表:
年份
2012
2013
2014
2015
2016
2017
年份
代码t
1
2
3
4
5
6
年产量
y(万吨)
6.6
6.7
7
7.1
7.2
7.4
(1)根据表中数据,建立关于t的线性回归方程
;
(2)根据线性回归方程预测2019年该地区该农产品的年产量.
(参考数据:
计算结果保留小数点后两位)
【解析】(1)由题意可知:
+0.52+1.52+2.52=17.5,所以
=0.16,
又
=7-0.16×3.5=6.44,
所以y关于t的线性回归方程为
=0.16t+6.44.
(2)由(1)可得,当年份为2019年时,年份代码t=8,
此时
=0.16×8+6.44=7.72,所以,可预测2019年该地区该农产品的年产量
约为7.72万吨.
【考场秘技】
1.求线性回归方程的关键是确定回归系数
,应充分利用回归直线过样本点中
心
,而所有样本点可能都不在直线上.
2.根据线性回归方程计算的
值,仅是一个预报值,而不是真实发生的值.
3.求线性回归方程的关键
(1)正确理解计算
的公式和准确计算.
(2)在分析两个变量的相关关系时,可根据样本数据作出散点图来确定两个变量
之间是否具有相关关系,若具有线性相关关系,则可通过线性回归方程估计和预
测变量的值.
4.独立性检验的关键
(1)根据2×2列联表准确计算K2的观测值k,若2×2列联表没有列出来,要先列出此表.
(2)K2的观测值k越大,则两类分类变量有关的把握越大,犯错的概率越小.
【万能模板】
独立性验证的步骤:
(1)列出2×2列联表:注意求出各行各列的总值,方便计算;
(2)将表中数据代入K2公式,计算出K2的观测值k;
(3)根据k的值参考表格,求出相关的概率;
(4)下结论.
【阅卷点评】
1.步骤分:(1)相关性系数公式;(2)K2公式.
2.关键分:解题过程的关键点,有则给分,无则没分.如选择分层抽样的依据为各个地块物种数量差异性很大.
3.计算分:用平均值估计这种野生动物数量的总值,相关系数的求解.
4.注意区分分层抽样与简单随机抽样,如:(1)整体分成了有明显差异的几部分,要选择分层抽样,(2)如果个体的差异不明显,可以选择简单随机抽样.
1.(独立性检验)在新冠肺炎疫情期间,为了指导不同人群科学合理地选择和使用
口罩,现对N95口罩的了解情况进行调查.现随机抽取40人进行调查,其中45岁以
下的有20人.在接受调查的40人中,对于N95这种口罩了解的占50%,在了解的人中
45岁以上(含45岁)的人数占
.
(1)将列联表补充完整;
高考演兵场·检验考试力
了解
不了解
总计
45岁以下
45岁以上(含45岁)
总计
40
(2)判断是否有99%的把握认为对N95这种口罩的了解与否与年龄有关.
参考公式:K2=
,其中n=a+b+c+d.
参考数据:
P(K2≥k0)
0.10
0.05
0.010
0.001
k0
2.706
3.841
6.635
10.828
1.【解析】(1)由题意可得对于N95这种口罩了解的人数为40×50%=20,则45岁以
上(含45岁)的人对N95这种口罩了解的人数为20×
=5.故补充列联表如下:
了解
不了解
总计
45岁以下
15
5
20
45岁以上(含45岁)
5
15
20
总计
20
20
40
(2)由题意可得,K2的观测值k=
=10,
因为10>6.635,所以有99%的把握认为对N95这种口罩的了解与否与年龄有关.
2.(回归分析)随着智能手机的普及,使用手机上网成为人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价x(单位:元/月)和购买人数y(单位:万人)的关系如表:
流量包的定
价x(元/月)
30
35
40
45
50
购买人数y(万人)
18
14
10
8
5
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟
合y与x的关系?并指出是正相关还是负相关;
(2)①求出y关于x的回归方程;
②若该通信公司在一个类似于试点的城市中将这款流量包的价格定为25元/月,
请用所求回归方程预测该市一个月内购买该流量包的人数能否超过20万人.
参考数据:
2.【解析】(1)根据题意,得
可列表如下
根据表格和参考数据,得
因而相关系数
由于
≈0.99,很接近1,因而可以用线性回归方程模型拟合y与x的关系.
由于r<0,故其关系为负相关.
(2)①
=11+0.64×40=36.6,
因而y关于x的回归方程为
=-0.64x+36.6.
②由①知,若x=25,则
=-0.64×25+36.6=20.6>20,故若将流量包的价格定为
25元/月,可预测该市一个月内购买该流量包的人数会超过20万人.
3.(独立性检验)2019年12月1日起郑州市施行《郑州市城市生活垃圾分类管理办法》,郑州正式进入城市生活垃圾分类时代.为了增强社区居民对垃圾分类知识的了解,积极参与到垃圾分类的行动中,某社区采用线下和线上相结合的方式开展了一次200名辖区成员参加的“垃圾分类有关知识”专题培训.为了了解参训成员对于线上培训、线下培训的满意程度,社区居委会随机选取了40名辖区成员,将他们分成两组,每组20人,分别对线上、线下两种培训进行满意度测评,根据辖区成员的评分(满分100分)绘制了如图所示的茎叶图.
(1)根据茎叶图判断辖区成员对于线上、线下哪种培训的满意度更高,并说明理由.
(2)求这40名辖区成员满意度评分的中位数m,并将评分不超过m、超过m分别视为“基本满意”“非常满意”两个等级.
(ⅰ)利用样本估计总体的思想,估算本次培训共有多少辖区成员对线上培训非常满意;
(ⅱ)根据茎叶图填写下面的列联表.
基本满意
非常满意
总计
线上培训
线下培训
总计
并根据列联表判断能否有99.5%的把握认为辖区成员对两种培训方式的满意度有差异?
3.【解析】(1)由茎叶图可知,线上培训的满意度评分在茎7上的最多,关于茎7大
致呈对称分布,线下培训的满意度评分分布在茎8上的最多,关于茎8大致呈对称
分布,故可以认为线下培训满意度评分比线上培训满意度评分更高,因此辖区成
员对线下培训的满意度更高.
(2)由茎叶图知m=
=80.
(ⅰ)参加线上培训满意度调查的20名辖区成员中共有6名成员对线上培训非常满
意,频率为
,又本次培训共200名成员参加,所以对线上培训非常满意的成员约
有200×
=60(人).
(ⅱ)列联表如下:
基本满意
非常满意
总计
线上培训
14
6
20
线下培训
6
14
20
总计
20
20
40
于是K2的观测值k=
=6.4,由于6.4<7.879,
所以没有99.5%的把握认为辖区成员对两种培训方式的满意度有差异.
4.(独立性检验)2020年3月,因为新冠肺炎疫情的影响,我市全体学生只能在网上在线学习,为了研究学生在线学习情况,市教研院数学学科随机从市区各高中学校抽取120名学生对线上教学情况进行调查(其中,男生与女生的人数之比为3∶1),结果发现:男生中有40名对于线上教学满意,女生中有10名表示对于线上教学不满意.
(1)请完成如表2×2列联表,并回答能否有95%的把握认为“对线上教学是否满意与性别有关”;
态度性别
满意
不满意
总计
男生
女生
总计
120
(2)采用分层抽样的方法,从被调查的对线上教学满意的学生中,抽取6名学生,再从这6名学生中抽取2名学生,作线上学习的经验介绍,求所选取的2名学生性别不同的概率.
4.【解析】(1)由题意可知抽取的120名学生中男生有90人,女生有30人,则列联
表如下:
K2的观测值k=
≈4.4>3.841,则有95%的把握认为“对线上教
学是否满意与性别有关”.
态度性别
满意
不满意
总计
男生
40
50
90
女生
20
10
30
总计
60
60
120
(2)由分层抽样的性质可知,抽取的6名学生中,男生4人,女生2人,
记4名男生分别为a,b,c,d,2名女生分别为A,B,
从这6名学生中抽取2名学生的所有情况为:
,{c,d},{c,A},{c,B},
{d,A},{d,B},{A,B},共15种,
其中所选取的2名学生性别不同的共有8种,
则所选取的2名学生性别不同的概率P=
.
5.(回归分析)某电子科技公司由于产品采用最新技术,销售额不断增长,最近5个季度的销售额数据统计如下表(其中2018Q1表示2018年第一季度,以此类推):
季度
2018Q1
2018Q2
2018Q3
2018Q4
2019Q1
季度编号x
1
2
3
4
5
销售额y(百万元)
46
56
67
86
96
(1)公司市场部从中任选2个季度的数据进行对比分析,求这2个季度的销售额
都超过6千万元的概率;
(2)求y关于x的线性回归方程,并预测该公司2019Q3的销售额.
附:线性回归方程
.
参考数据:
=1
183.
5.【解析】(1)从5个季度的数据中任选2个,这2个季度的销售额有10种情况:(46,56),(46,67),(46,86),(46,96),(56,67),(56,86),(56,96),(67,86),
(67,96),(86,96).
设“这2个季度的销售额都超过6千万元”为事件A,事件A包含(67,86),(67,96),
(86,96),共3种情况.
所以P(A)=
.
(2)
(1+2+3+4+5)=3,
(46+56+67+86+96)=70.2.
所以
=31.2.
所以y关于x的线性回归方程为
=13x+31.2.令x=7,
得
=13×7+31.2=122.2(百万元).
所以预测该公司2019Q3的销售额为122.2百万元.
6.(独立性检验)今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严
控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员100人,其中50岁
及以上的共有40人.这100人中确诊的有10名,其中50岁以下的人占
.
确诊患新冠肺炎
未确诊患新冠肺炎
总计
50岁及以上
40
50岁以下
总计
10
100
(1)请将列联表补充完整,并判断是否有95%的把握认为是否确诊患新冠肺炎与年龄有关;
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,若从这5人中随机抽取3人,求恰有2人为50岁及以上的概率.
6.【解析】(1)因为100人中确诊的有10名,其中50岁以下的人占
,
所以50岁以下的确诊人数为4,50岁及以上的确诊人数为6.
因为50岁及以上的共有40人,
列联表补充如下,
确诊患新
冠肺炎
未确诊患
新冠肺炎
总计
50岁及
以上
6
34
40
50岁
以下
4
56
60
总计
10
90
100
则K2的观测值k=
≈1.852<3.841,所以没有95%的把握认为是
否确诊患新冠肺炎与年龄有关.
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,则抽取的5人中,有3人
50岁及以上,分别记作a,b,c;2人50岁以下,记作d,e.从中任取3人,可能的不同结
果有:
abc,abd,abe;acd,ace;ade;bcd,bce;bde;cde,共10种不同的情况,
恰有两人为50岁及以上的情况有abd,abe,acd,ace,bcd,bce,共6种不同的情况,
由于每种情况都是等可能的,所以恰有2人为50岁及以上的概率为
.
7.(回归分析)某单位响应党中央“精准扶贫”号召,对某村6户贫困户中的甲户进行定点帮扶,每年跟踪调查统计一次,从2015年1月1日至2018年12月底统计数据如下(人均年纯收入):
年份
2015年
2016年
2017年
2018年
年份代码x
1
2
3
4
收入y(百元)
25
28
32
35
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均
年纯收入为3
747元)
(2)2019年初,根据扶贫办的统计知,该村剩余5户贫困户中还有2户没有脱贫,
现从这5户中抽取2户,求至少有一户没有脱贫的概率.
7.【解析】(1)根据表格中数据可得,
=30,
xiyi=1×25+2×28+3×32+4×35=317,
=12+22+32+42=30,
所以
所以y关于x的线性回归方程是
=3.4x+21.5,当x=5时,
=38.5(百元),
因为3
850>3
747,所以甲户在2019年能够脱贫.
(2)设没有脱贫的2户为A,B,另3户为C,D,E,所有可能的情况
为:AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共有10种.其中至少有一户没有脱贫的情
况有7种.所以至少有一户没有脱贫的概率为
.
8.(独立性检验)2011年,国际数学协会正式宣布,将每年的3月14日设为国际数学
节,来源是中国古代数学家祖冲之的圆周率,为庆祝该节日,某校举办数学趣味知
识竞赛活动,参与竞赛的文科生与理科生人数之比为1∶3,且成绩分布在
,
分数在
分别获二等奖和一等奖.按文理科用分层抽样的方法抽取
200人的成绩作为样本,得到成绩的频率分布直方图.
(1)填写下面的2×2列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
文科生
理科生
总计
获奖
5
不获奖
总计
200
(2)将上述调查所得的频率视为概率,现从参赛学生中,通过分层抽样的方法从这些获奖人中随机抽取4人,再从这4人中任意选取2人,求2人均获二等奖的概率.
8.【解析】(1)补全2×2列联表如下.
K2的观测值k=
≈4.167>3.841.所以有超过95%的把握认为
“获奖与学生的文理科有关”.
文科生
理科生
总计
获奖
5
35
40
不获奖
45
115
160
总计
50
150
200
(2)由已知可得,分数在[80,90)获二等奖的参赛学生中抽取3人,分数
在[90,100]获一等奖的参赛学生中抽取1人.
记获二等奖的3人分别为a,b,c,获一等奖的1人为A,事件E为“从这4人中抽取2人
且这2人均获二等奖”.
从这4人中随机抽取2人的基本事件为
共6种,
其中2人均获二等奖的情况有
共3种,由古典概型的概率计算公式
得P
.
故2人均获二等奖的概率为
.
同课章节目录
