导数与不等式成立课件(共49张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 导数与不等式成立课件(共49张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 782.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 20:31:43 | ||
图片预览











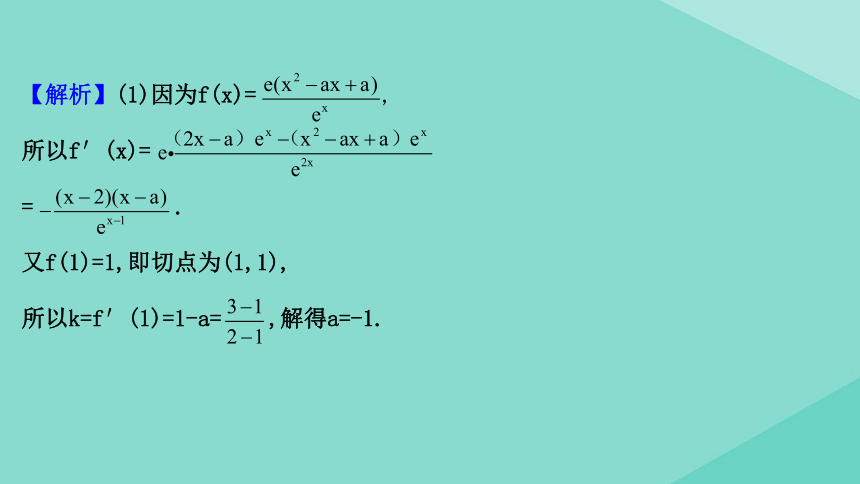
文档简介
导数与不等式成立
真题再研析·提升审题力
【典例】(12分)(2019·全国Ⅰ卷)已知函数f(x)=2sin x-xcos x-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)上存在唯一零点.
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
【审题·正向思维】
(1)函数求导→确定零点→由零点存在定理判断出唯一零点所处的位置→证得结论;
(2)构造函数h(x)=f(x)-ax→二次求导→分类讨论→判断h(x)单调性→确定h(x)≥0恒成立→求a的取值范围.
【标准答案】(1)f′(x)=cos x+xsin x-1,
令g(x)=cos x+xsin x-1,
则g′(x)=xcos x,………………………………………………………………2分
当x∈ 时,令g′(x)=0,解得:x= ,
所以当x∈ 时,g′(x)>0;
当x∈ 时,g′(x)<0,所以g(x)在 上单调递增;在 上单调递减,
又g(0)=0,g = -1>0,g =-2,
所以f′(x)在 上无零点. …………………………………………………4分
因为g ·g <0,所以?x0∈ ,
g(x0)=0,又g(x)在 上单调递减,
所以x=x0为g(x)在 上的唯一零点,
即f′(x)在 上的唯一零点,
综上,f′(x)在区间 上存在唯一零点. ……………………………………5分
(2)若x∈ 时,f(x)≥ax,
即f(x)-ax≥0恒成立,
令h(x)=f(x)-ax=2sin x-xcos x-(a+1)x,
则h′(x)=cos x+xsin x-1-a,h″(x)=xcos x=g′(x),
由(1)可知,h′(x)在 上单调递增;
在 上单调递减,
且h′(0)=-a,h′ = -a,h′ =-2-a,
所以h′(x)min=h′ =-2-a,h′(x)max=
h′ = -a. …………………………………………………………………7分
①当a≤-2时,h′(x)min=h′ =-2-a≥0,即
h′(x)≥0在 上恒成立,所以h(x)在 上单调递增,所以h(x)≥h(0)=0,即
f(x)-ax≥0,此时f(x)≥ax恒成立; ……………………………………………8分
②当-20,h′ <0,所以?x1∈ ,使得h′(x1)=0,
所以h(x)在 上单调递增,在 上单调递减,又h(0)=0,h =2sin π-
πcos π-(a+1)π=-aπ≥0,所以h(x)≥0在 上恒成立,即f(x)≥ax恒成
立; …………………………………………………………………………………9分
③当00,
所以?x2∈ ,使得h′(x2)=0,所以h(x)在 上单调递减,在 上单
调递增,所以x∈(0.x2)时,h(x)④当a≥ 时,h′(x)max=h′ = -a≤0;
所以h(x)在 上单调递减,
所以h(x)可知f(x)≥ax不恒成立,综上所述:a∈ .
……………………………………………………………………………………12分
【深度解读】
测试目标
(1)函数求导,存在性定理;
(2)构造函数,分类讨论,利用单调性求参数的取值范围
测试目标
数学抽象:恒成立确定a的范围;
逻辑推理:根据存在性定理确定唯一零点;
数学建模:构造函数;
数学运算:求导数,解不等式,化简
【模拟考场】
设函数f(x)= (a∈R).
(1)若曲线y=f(x)在x=1处的切线过点M(2,3),求a的值;
(2)设g(x)=x+ ,若对任意的n∈[0,2],存在m∈[0,2],使得f(m)≥g(n)成
立,求a的取值范围.
【解析】(1)因为f(x)=
所以f′(x)=
= .
又f(1)=1,即切点为(1,1),
所以k=f′(1)=1-a= ,解得a=-1.
(2)“对任意的n∈[0,2],存在m∈[0,2],使得f(m)≥g(n)成立”,等价于“在
[0,2]上,f(x)的最大值大于或等于g(x)的最大值”.
因为g(x)=x+ ,所以g′(x)= ≥0,
所以g(x)在[0,2]上单调递增,所以g(x)max=g(2)=2.
令f′(x)=0,得x=2或x=a.
①当a≤0时,f′(x)≥0在[0,2]上恒成立,f(x)单调递增,
f(x)max=f(2)=(4-a)e-1≥2,解得a≤4-2e;
②当0f′(x)≥0在[a,2]上恒成立,f(x)单调递增,
f(x)的最大值为f(2)=(4-a)e-1或f(0)=ae,
所以(4-a)e-1≥2或ae≥2.
解得:a≤4-2e或a≥ ,所以 ≤a<2;
③当a≥2时,f′(x)≤0在[0,2]上恒成立,f(x)单调递减,
f(x)max=f(0)=ae≥2,解得a≥ ,所以a≥2.
综上所述:a≤4-2e或a≥ .
【考场秘籍】
1.证明不等式的两个技巧
(1)利用单调性:若f(x)在[a,b]上是增函数,则①?x∈[a,b],有f(a)≤f(x)≤f(b),②?x1,x2∈[a,b],且x1(2)利用最值:若f(x)在某个范围D内有最大值M(或最小值m),则?x∈D,有f(x)≤M(或f(x)≥m).
2.巧解不等式的“恒成立”与“存在性”问题.
(1)f(x)>g(x)对一切x∈I恒成立:I是f(x)>g(x)的解集的子集,
[f(x)-g(x)]min>0(x∈I).
(2)?x0∈I,使f(x0)>g(x0)成立:I与f(x)>g(x)的解集的交集不是空集,[f(x)-
g(x)]max>0(x∈I).
(3)对?x1,x2∈I使得f(x1)≤g(x2)?f(x)max≤g(x)min.
(4)对?x1,x2∈I使得f(x1)≥g(x2),f(x)min≥g(x)max.
【万能模板】
利用导数证明不等式的步骤
第一步 求导数:函数求导化简,求出导函数的零点;
第二步 明单调:解不等式,确定单调区间;
第三步 定零点:利用零点存在性定理;
第四步 分情况:对a讨论,使不等式成立;
第五步 得结论:对a的情况进行整合(求并集),得到原题结论.
【阅卷点评】
得步骤分:“步步为赢”,求得满分.如第(1)问中,求导正确,分析单调性;
得关键分:解题过程不可忽视关键点,有则给分,无则没分,如第(2)问中求出最大值和最小值;
得计算分:解题过程中计算准确是得满分的根本保证.
1.(极值与恒成立)已知函数f(x)=ln x-ax,g(x)=x2,a∈R.
(1)求函数f(x)的极值点;
(2)若f(x)≤g(x)恒成立,求a的取值范围.
高考演兵场·检验考试力
【解析】(1)f(x)=ln x-ax的定义域为(0,+∞),f′(x)= -a,
当a≤0时,f′(x)= -a>0,所以f(x)在(0,+∞)上单调递增,无极值点,
当a>0时,解f′(x)= -a>0得0 ,
所以f(x)在 上单调递增,在 上单调递减,
所以函数f(x)有极大值点 ,无极小值点.
(2)由条件可得ln x-x2-ax≤0(x>0)恒成立,
则当x>0时,a≥ -x恒成立,
令h(x)= -x(x>0),则h′(x)=
令k(x)=1-x2-ln x(x>0),
则当x>0时,k′(x)=-2x- <0,
所以k(x)在(0,+∞)上为减函数.
又k(1)=0,所以在(0,1)上,h′(x)>0;在(1,+∞)上,h′(x)<0.
所以h(x)在(0,1)上为增函数;在(1,+∞)上为减函数.
所以h(x)max=h(1)=-1,所以a≥-1,即a的取值范围为[-1,+∞).
2.(单调性与恒成立)已知a∈R,f(x)=2x-aln x.
(1)讨论f(x)的单调性;
(2)当x≥1时,xf(x)≥x2+1恒成立,求实数a的取值范围.
【解析】(1)f(x)的定义域是(0,+∞),
f′(x)=2-
当a≤0时,f′(x)>0,f(x)在(0,+∞)上递增,
当a>0时,在 上,f′(x)<0,f(x)递减,
在 上,f′(x)>0,f(x)递增,
综上,当a≤0时,f(x)在(0,+∞)上递增,
当a>0时,f(x)在 上递减,在 上递增;
(2)xf(x)≥x2+1恒成立,即xf(x)-(x2+1)≥0恒成立,
设g(x)=xf(x)-(x2+1),则g(x)=x2-axln x-1,
g′(x)=2x-a(1+ln x),g′(x)的单调性和f(x)相同,
当a≤0时,g′(x)在 上递增,g′(x)≥g′(1)=2-a>0,
故g(x)在 上递增,g(x)≥g(1)=0,
当a>0时,g′(x)在 上递减,在 上递增,
当0g′(x)≥g′(1)=2-a≥0,
故g(x)在[1,+∞)上是增函数,故g(x)≥g(1)=0,
当a>2时,在区间 上,g′(x)递减,
故g′(x)故g(x)在[1,+∞)上递减,故g(x)综上,a的范围是 .
3.(证明不等式)已知函数f(x)=ln x+ax-1(a∈R).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)图象过点(1,0),求证:e-x+xf(x)≥0.
【解析】(1)函数f(x)的定义域为 ,f′(x)= +a= .
当a≥0时,f′(x)>0,f(x)在 上单调递增;
当a<0时,由f′(x)=0,得x= .
若x∈ ,则f′(x)>0,f(x)单调递增;
若x∈ ,则f′(x)<0,f(x)单调递减.
综上所述:当a≥0时,f(x)在 上单调递增;
当a<0时,f(x)在 上单调递增,在 上单调递减.
(2)由函数f(x)的图象过点(1,0),可得a=1,
此时f(x)=ln x+x-1,
要证e-x+xf(x)≥0,即证 e-x+ln x+x-1≥0.
令g(x)= e-x+ln x+x-1(x>0),g′(x)=
又令y=xex-1,y′=(x+1)ex,
当x∈(0,+∞)时,y′>0,y=xex-1在(0,+∞)上单调递增.
由g′(x)=0,得xex-1=0,
故存在x0∈(0,+∞)使得x0 =1,
此时 = ,故x0=-ln x0,
当x∈ 时,g′(x)<0;
当x∈(x0,+∞)时,g′(x)>0.
所以g(x)在 上递减,在(x0,+∞)上递增,
当x=x0时,g(x)有最小值g(x0)= +ln x0+x0-1=0,
故e-x+xf(x)≥0成立.
4.(与数列结合)已知函数f(x)=ln x-ax+1(a∈R).
(1)若对任意x∈(0,+∞),f(x)≤0恒成立,求a的取值范围.
(2)求证: .
【解析】(1)f′(x)= -a=
若a≤0,当x>1时,ln x-ax+1>0,不符合题意;
若a>0,由f′(x)>0得0 ,
所以f(x)在 上递增,在 上递减,
所以f(x)max=f =ln -a· +1=ln ≤0,
所以ln a≥0,a≥1,
所以a的取值范围 .
(2)由(1)知,当a=1时,ln x≤x-1(x>0),
所以ln
ln +ln +…+
而
所以
所以
5.(双变量问题)已知函数f(x)=xln x- mx2 ,g(x)=- .
(1)若函数f(x)在(1,f(1))处的切线与直线x-y+1=0平行,求m;
(2)证明:在(1)的条件下,对任意x1,x2∈(0,+∞),f(x1)>g(x2)成立.
【解析】(1)f(x)的定义域为(0,+∞),
f′(x)=ln x+1-mx,f′(1)=1-m,
因为f(x)在(1,f(1))处的切线与直线x-y+1=0平行,
所以1-m=1,
即m=0;
(2)在(1)的条件下,f(x)=xln x,可得f′(x)=ln x+1,
当x∈ 时,f′(x)<0,f(x)单调递减,
当x∈ 时,f′(x)>0,f(x)单调递增,
所以f(x)=xln x在x= 时取得最小值f =- ,
可知f(x1)≥- ,
由g(x)=
令h(x)=g′(x)=
所以当x∈(0,1)时,h′(x)>0,h(x)单调递增,
当x∈(1,+∞)时,h′(x)<0,h(x)单调递减,
所以g′(x)≤g′(1)=h(1)=- ,
因为g′(x)≤- <0,所以g(x)在(0,+∞)上单调递减,
可知g(x2)所以对任意x1,x2∈(0,+∞),f(x1)>g(x2).
6.(极值点偏移)已知函数f(x)=4x-aln x- x2-2,其中a为正实数.
(1)求函数y=f(x)的单调区间;
(2)若函数y=f(x)有两个极值点x1,x2,求证:f(x1)+f(x2)<6-ln a.
【解析】(1)因为函数f(x)=4x-aln x- x2-2,
所以f′(x)=4- 函数y=f(x)的定义域为(0,+∞),
令t=x2-4x+a,
①若16-4a≤0,即a≥4时,则f′(x)≤0,此时f(x)的单调减区间为(0,+∞);
②若16-4a>0,即0令f′(x)=0,得x=2± ,
当02+ 时,f′(x)<0,
当2-0,此时f(x)的单调减区间为(0,2- ),(2+
),
单调增区间为(2- ,2+ ).
(2)由(1)知,当0因为f(x1)+f(x2)=4x1-aln x1- -2+4x2-aln x2- -2
=4(x1+x2)-aln(x1x2)-
=16-aln a- (42-2a)-4=4+a-aln a,
要证f(x1)+f(x2)<6-ln a,只需证aln a-a-ln a+2>0.
构造函数g(x)=xln x-x-ln x+2,
则g′(x)=1+ln x-1- =ln x- ,
g′(x)在(0,4)上单调递增,又g′(1)=-1<0,g′(2)=ln 2- >0,且g′(x)在定义
域上不间断,
由零点存在性定理,可知g′(x)=0在(1,2)上有唯一实根x0,且ln x0= .
则g(x)在(0,x0)上递减,在(x0,4)上递增,所以g(x)的最小值为g(x0),
因为g(x0)=1-x0- +2=3- ,
当x0∈(1,2)时,x0+ ∈ ,则g(x0)>0,
所以g(x)≥g(x0)>0恒成立.
所以aln a-a-ln a+2>0,
所以f(x1)+f(x2)<6-ln a,得证.
7.(存在性问题)已知函数f(x)= +aln x(a≠0,a∈R).
(1)若a=1,求函数f(x)的极值和单调区间;
(2)若在区间(0,e]上至少存在一点x0,使得f(x0)<0成立,求实数a的取值范围.
【解析】f(x)= +aln x(a≠0,a∈R)的定义域为(0,+∞),
因为f′(x)= .
(1)当a=1时,f′(x)= ,令f′(x)=0,得x=1,
又f(x)的定义域为(0,+∞),
f′(x),f(x)随x的变化情况如表:
x
(0,1)
1
(1,+∞)
f′(x)
-
0
+
f(x)
单调递减
极小值
单调递增
所以x=1时,f(x)取得极小值为1.
f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1).
(2)因为f′(x)=- ,且a≠0.
令f′(x)=0,得x= ,
若在区间(0,e]上存在一点x0,使得f(x0)<0成立,
其充要条件是f(x)在区间(0,e]上的最小值小于0即可.
(i)当x= <0,即a<0时,f′(x)<0对x∈(0,e]成立,
所以,f(x)在区间(0,e]上单调递减,
故f(x)在区间(0,e]上的最小值为f(e)= +aln e= +a,
由 +a<0,得a<- ,即a∈ .
(ii)当x= >0,即a>0时,
若e≤ ,则f′(x)≤0对x∈(0,e]成立,
所以f(x)在区间(0,e]上单调递减,
所以,f(x)在区间(0,e]上的最小值为
f(e)= +aln e= +a>0,
显然,f(x)在区间(0,e]上的最小值小于0不成立.
若0< 时,则有
所以f(x)在区间(0,e]上的最小值为f =a+aln .
由f =a+aln =a(1-lna)<0,
得1-lna<0,解得a>e,即a∈(e, ).
综上可知a∈ ∪ (e, ).符合题意.
x
(0, )
( ,e]
f′(x)
-
0
+
f(x)
单调递减
极小值
单调递增
8.(探索问题)已知函数f(x)= -3,g(x)=aln x-2x(a∈R).
(1)讨论g(x)的单调性;
(2)是否存在实数a,使不等式f(x)≥g(x)恒成立?如果存在,求出a的值;如果不存
在,请说明理由.
【解析】(1)g′(x)= ,x>0,
(i)当a≤0时,g′(x)<0,函数在(0,+∞)上单调递减,
(ii)当a>0时,令g′(x)>0得0 a,
所以函数g(x)在 上单调递增,在 上单调递减.
(2)要使不等式f(x)≥g(x)恒成立,即 -3≥aln x-2x恒成立,
即xex-aeln x+2ex-3e≥0恒成立,
令u(x)=xex-aeln x+2ex-3e,则u(1)=0,
要使得原不等式成立,则u(x)在x=1处取得最小值且是极小值,
因为u′(x)=
所以u′(1)=0可得a=4,
检验a=4时,u′(x)=
设v(x)=x(x+1)ex+2ex-4e,且v(1)=0,
显然v(x)在(0,+∞)上单调递增,
当x∈(0,1)时,v(x)<0,即u′(x)<0,u(x)单调递减,当x∈(1,+∞)时,v(x)>0,即u′(x)>0,u(x)单调递增,
故u(x)的最小值u(1)=0,满足题意,
综上,a=4.
真题再研析·提升审题力
【典例】(12分)(2019·全国Ⅰ卷)已知函数f(x)=2sin x-xcos x-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)上存在唯一零点.
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
【审题·正向思维】
(1)函数求导→确定零点→由零点存在定理判断出唯一零点所处的位置→证得结论;
(2)构造函数h(x)=f(x)-ax→二次求导→分类讨论→判断h(x)单调性→确定h(x)≥0恒成立→求a的取值范围.
【标准答案】(1)f′(x)=cos x+xsin x-1,
令g(x)=cos x+xsin x-1,
则g′(x)=xcos x,………………………………………………………………2分
当x∈ 时,令g′(x)=0,解得:x= ,
所以当x∈ 时,g′(x)>0;
当x∈ 时,g′(x)<0,所以g(x)在 上单调递增;在 上单调递减,
又g(0)=0,g = -1>0,g =-2,
所以f′(x)在 上无零点. …………………………………………………4分
因为g ·g <0,所以?x0∈ ,
g(x0)=0,又g(x)在 上单调递减,
所以x=x0为g(x)在 上的唯一零点,
即f′(x)在 上的唯一零点,
综上,f′(x)在区间 上存在唯一零点. ……………………………………5分
(2)若x∈ 时,f(x)≥ax,
即f(x)-ax≥0恒成立,
令h(x)=f(x)-ax=2sin x-xcos x-(a+1)x,
则h′(x)=cos x+xsin x-1-a,h″(x)=xcos x=g′(x),
由(1)可知,h′(x)在 上单调递增;
在 上单调递减,
且h′(0)=-a,h′ = -a,h′ =-2-a,
所以h′(x)min=h′ =-2-a,h′(x)max=
h′ = -a. …………………………………………………………………7分
①当a≤-2时,h′(x)min=h′ =-2-a≥0,即
h′(x)≥0在 上恒成立,所以h(x)在 上单调递增,所以h(x)≥h(0)=0,即
f(x)-ax≥0,此时f(x)≥ax恒成立; ……………………………………………8分
②当-2
所以h(x)在 上单调递增,在 上单调递减,又h(0)=0,h =2sin π-
πcos π-(a+1)π=-aπ≥0,所以h(x)≥0在 上恒成立,即f(x)≥ax恒成
立; …………………………………………………………………………………9分
③当0
所以?x2∈ ,使得h′(x2)=0,所以h(x)在 上单调递减,在 上单
调递增,所以x∈(0.x2)时,h(x)
所以h(x)在 上单调递减,
所以h(x)
……………………………………………………………………………………12分
【深度解读】
测试目标
(1)函数求导,存在性定理;
(2)构造函数,分类讨论,利用单调性求参数的取值范围
测试目标
数学抽象:恒成立确定a的范围;
逻辑推理:根据存在性定理确定唯一零点;
数学建模:构造函数;
数学运算:求导数,解不等式,化简
【模拟考场】
设函数f(x)= (a∈R).
(1)若曲线y=f(x)在x=1处的切线过点M(2,3),求a的值;
(2)设g(x)=x+ ,若对任意的n∈[0,2],存在m∈[0,2],使得f(m)≥g(n)成
立,求a的取值范围.
【解析】(1)因为f(x)=
所以f′(x)=
= .
又f(1)=1,即切点为(1,1),
所以k=f′(1)=1-a= ,解得a=-1.
(2)“对任意的n∈[0,2],存在m∈[0,2],使得f(m)≥g(n)成立”,等价于“在
[0,2]上,f(x)的最大值大于或等于g(x)的最大值”.
因为g(x)=x+ ,所以g′(x)= ≥0,
所以g(x)在[0,2]上单调递增,所以g(x)max=g(2)=2.
令f′(x)=0,得x=2或x=a.
①当a≤0时,f′(x)≥0在[0,2]上恒成立,f(x)单调递增,
f(x)max=f(2)=(4-a)e-1≥2,解得a≤4-2e;
②当0
f(x)的最大值为f(2)=(4-a)e-1或f(0)=ae,
所以(4-a)e-1≥2或ae≥2.
解得:a≤4-2e或a≥ ,所以 ≤a<2;
③当a≥2时,f′(x)≤0在[0,2]上恒成立,f(x)单调递减,
f(x)max=f(0)=ae≥2,解得a≥ ,所以a≥2.
综上所述:a≤4-2e或a≥ .
【考场秘籍】
1.证明不等式的两个技巧
(1)利用单调性:若f(x)在[a,b]上是增函数,则①?x∈[a,b],有f(a)≤f(x)≤f(b),②?x1,x2∈[a,b],且x1
2.巧解不等式的“恒成立”与“存在性”问题.
(1)f(x)>g(x)对一切x∈I恒成立:I是f(x)>g(x)的解集的子集,
[f(x)-g(x)]min>0(x∈I).
(2)?x0∈I,使f(x0)>g(x0)成立:I与f(x)>g(x)的解集的交集不是空集,[f(x)-
g(x)]max>0(x∈I).
(3)对?x1,x2∈I使得f(x1)≤g(x2)?f(x)max≤g(x)min.
(4)对?x1,x2∈I使得f(x1)≥g(x2),f(x)min≥g(x)max.
【万能模板】
利用导数证明不等式的步骤
第一步 求导数:函数求导化简,求出导函数的零点;
第二步 明单调:解不等式,确定单调区间;
第三步 定零点:利用零点存在性定理;
第四步 分情况:对a讨论,使不等式成立;
第五步 得结论:对a的情况进行整合(求并集),得到原题结论.
【阅卷点评】
得步骤分:“步步为赢”,求得满分.如第(1)问中,求导正确,分析单调性;
得关键分:解题过程不可忽视关键点,有则给分,无则没分,如第(2)问中求出最大值和最小值;
得计算分:解题过程中计算准确是得满分的根本保证.
1.(极值与恒成立)已知函数f(x)=ln x-ax,g(x)=x2,a∈R.
(1)求函数f(x)的极值点;
(2)若f(x)≤g(x)恒成立,求a的取值范围.
高考演兵场·检验考试力
【解析】(1)f(x)=ln x-ax的定义域为(0,+∞),f′(x)= -a,
当a≤0时,f′(x)= -a>0,所以f(x)在(0,+∞)上单调递增,无极值点,
当a>0时,解f′(x)= -a>0得0
所以f(x)在 上单调递增,在 上单调递减,
所以函数f(x)有极大值点 ,无极小值点.
(2)由条件可得ln x-x2-ax≤0(x>0)恒成立,
则当x>0时,a≥ -x恒成立,
令h(x)= -x(x>0),则h′(x)=
令k(x)=1-x2-ln x(x>0),
则当x>0时,k′(x)=-2x- <0,
所以k(x)在(0,+∞)上为减函数.
又k(1)=0,所以在(0,1)上,h′(x)>0;在(1,+∞)上,h′(x)<0.
所以h(x)在(0,1)上为增函数;在(1,+∞)上为减函数.
所以h(x)max=h(1)=-1,所以a≥-1,即a的取值范围为[-1,+∞).
2.(单调性与恒成立)已知a∈R,f(x)=2x-aln x.
(1)讨论f(x)的单调性;
(2)当x≥1时,xf(x)≥x2+1恒成立,求实数a的取值范围.
【解析】(1)f(x)的定义域是(0,+∞),
f′(x)=2-
当a≤0时,f′(x)>0,f(x)在(0,+∞)上递增,
当a>0时,在 上,f′(x)<0,f(x)递减,
在 上,f′(x)>0,f(x)递增,
综上,当a≤0时,f(x)在(0,+∞)上递增,
当a>0时,f(x)在 上递减,在 上递增;
(2)xf(x)≥x2+1恒成立,即xf(x)-(x2+1)≥0恒成立,
设g(x)=xf(x)-(x2+1),则g(x)=x2-axln x-1,
g′(x)=2x-a(1+ln x),g′(x)的单调性和f(x)相同,
当a≤0时,g′(x)在 上递增,g′(x)≥g′(1)=2-a>0,
故g(x)在 上递增,g(x)≥g(1)=0,
当a>0时,g′(x)在 上递减,在 上递增,
当0
故g(x)在[1,+∞)上是增函数,故g(x)≥g(1)=0,
当a>2时,在区间 上,g′(x)递减,
故g′(x)
3.(证明不等式)已知函数f(x)=ln x+ax-1(a∈R).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)图象过点(1,0),求证:e-x+xf(x)≥0.
【解析】(1)函数f(x)的定义域为 ,f′(x)= +a= .
当a≥0时,f′(x)>0,f(x)在 上单调递增;
当a<0时,由f′(x)=0,得x= .
若x∈ ,则f′(x)>0,f(x)单调递增;
若x∈ ,则f′(x)<0,f(x)单调递减.
综上所述:当a≥0时,f(x)在 上单调递增;
当a<0时,f(x)在 上单调递增,在 上单调递减.
(2)由函数f(x)的图象过点(1,0),可得a=1,
此时f(x)=ln x+x-1,
要证e-x+xf(x)≥0,即证 e-x+ln x+x-1≥0.
令g(x)= e-x+ln x+x-1(x>0),g′(x)=
又令y=xex-1,y′=(x+1)ex,
当x∈(0,+∞)时,y′>0,y=xex-1在(0,+∞)上单调递增.
由g′(x)=0,得xex-1=0,
故存在x0∈(0,+∞)使得x0 =1,
此时 = ,故x0=-ln x0,
当x∈ 时,g′(x)<0;
当x∈(x0,+∞)时,g′(x)>0.
所以g(x)在 上递减,在(x0,+∞)上递增,
当x=x0时,g(x)有最小值g(x0)= +ln x0+x0-1=0,
故e-x+xf(x)≥0成立.
4.(与数列结合)已知函数f(x)=ln x-ax+1(a∈R).
(1)若对任意x∈(0,+∞),f(x)≤0恒成立,求a的取值范围.
(2)求证: .
【解析】(1)f′(x)= -a=
若a≤0,当x>1时,ln x-ax+1>0,不符合题意;
若a>0,由f′(x)>0得0
所以f(x)在 上递增,在 上递减,
所以f(x)max=f =ln -a· +1=ln ≤0,
所以ln a≥0,a≥1,
所以a的取值范围 .
(2)由(1)知,当a=1时,ln x≤x-1(x>0),
所以ln
ln +ln +…+
而
所以
所以
5.(双变量问题)已知函数f(x)=xln x- mx2 ,g(x)=- .
(1)若函数f(x)在(1,f(1))处的切线与直线x-y+1=0平行,求m;
(2)证明:在(1)的条件下,对任意x1,x2∈(0,+∞),f(x1)>g(x2)成立.
【解析】(1)f(x)的定义域为(0,+∞),
f′(x)=ln x+1-mx,f′(1)=1-m,
因为f(x)在(1,f(1))处的切线与直线x-y+1=0平行,
所以1-m=1,
即m=0;
(2)在(1)的条件下,f(x)=xln x,可得f′(x)=ln x+1,
当x∈ 时,f′(x)<0,f(x)单调递减,
当x∈ 时,f′(x)>0,f(x)单调递增,
所以f(x)=xln x在x= 时取得最小值f =- ,
可知f(x1)≥- ,
由g(x)=
令h(x)=g′(x)=
所以当x∈(0,1)时,h′(x)>0,h(x)单调递增,
当x∈(1,+∞)时,h′(x)<0,h(x)单调递减,
所以g′(x)≤g′(1)=h(1)=- ,
因为g′(x)≤- <0,所以g(x)在(0,+∞)上单调递减,
可知g(x2)
6.(极值点偏移)已知函数f(x)=4x-aln x- x2-2,其中a为正实数.
(1)求函数y=f(x)的单调区间;
(2)若函数y=f(x)有两个极值点x1,x2,求证:f(x1)+f(x2)<6-ln a.
【解析】(1)因为函数f(x)=4x-aln x- x2-2,
所以f′(x)=4- 函数y=f(x)的定义域为(0,+∞),
令t=x2-4x+a,
①若16-4a≤0,即a≥4时,则f′(x)≤0,此时f(x)的单调减区间为(0,+∞);
②若16-4a>0,即0
当0
当2-
),
单调增区间为(2- ,2+ ).
(2)由(1)知,当0
=4(x1+x2)-aln(x1x2)-
=16-aln a- (42-2a)-4=4+a-aln a,
要证f(x1)+f(x2)<6-ln a,只需证aln a-a-ln a+2>0.
构造函数g(x)=xln x-x-ln x+2,
则g′(x)=1+ln x-1- =ln x- ,
g′(x)在(0,4)上单调递增,又g′(1)=-1<0,g′(2)=ln 2- >0,且g′(x)在定义
域上不间断,
由零点存在性定理,可知g′(x)=0在(1,2)上有唯一实根x0,且ln x0= .
则g(x)在(0,x0)上递减,在(x0,4)上递增,所以g(x)的最小值为g(x0),
因为g(x0)=1-x0- +2=3- ,
当x0∈(1,2)时,x0+ ∈ ,则g(x0)>0,
所以g(x)≥g(x0)>0恒成立.
所以aln a-a-ln a+2>0,
所以f(x1)+f(x2)<6-ln a,得证.
7.(存在性问题)已知函数f(x)= +aln x(a≠0,a∈R).
(1)若a=1,求函数f(x)的极值和单调区间;
(2)若在区间(0,e]上至少存在一点x0,使得f(x0)<0成立,求实数a的取值范围.
【解析】f(x)= +aln x(a≠0,a∈R)的定义域为(0,+∞),
因为f′(x)= .
(1)当a=1时,f′(x)= ,令f′(x)=0,得x=1,
又f(x)的定义域为(0,+∞),
f′(x),f(x)随x的变化情况如表:
x
(0,1)
1
(1,+∞)
f′(x)
-
0
+
f(x)
单调递减
极小值
单调递增
所以x=1时,f(x)取得极小值为1.
f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1).
(2)因为f′(x)=- ,且a≠0.
令f′(x)=0,得x= ,
若在区间(0,e]上存在一点x0,使得f(x0)<0成立,
其充要条件是f(x)在区间(0,e]上的最小值小于0即可.
(i)当x= <0,即a<0时,f′(x)<0对x∈(0,e]成立,
所以,f(x)在区间(0,e]上单调递减,
故f(x)在区间(0,e]上的最小值为f(e)= +aln e= +a,
由 +a<0,得a<- ,即a∈ .
(ii)当x= >0,即a>0时,
若e≤ ,则f′(x)≤0对x∈(0,e]成立,
所以f(x)在区间(0,e]上单调递减,
所以,f(x)在区间(0,e]上的最小值为
f(e)= +aln e= +a>0,
显然,f(x)在区间(0,e]上的最小值小于0不成立.
若0<
所以f(x)在区间(0,e]上的最小值为f =a+aln .
由f =a+aln =a(1-lna)<0,
得1-lna<0,解得a>e,即a∈(e, ).
综上可知a∈ ∪ (e, ).符合题意.
x
(0, )
( ,e]
f′(x)
-
0
+
f(x)
单调递减
极小值
单调递增
8.(探索问题)已知函数f(x)= -3,g(x)=aln x-2x(a∈R).
(1)讨论g(x)的单调性;
(2)是否存在实数a,使不等式f(x)≥g(x)恒成立?如果存在,求出a的值;如果不存
在,请说明理由.
【解析】(1)g′(x)= ,x>0,
(i)当a≤0时,g′(x)<0,函数在(0,+∞)上单调递减,
(ii)当a>0时,令g′(x)>0得0
所以函数g(x)在 上单调递增,在 上单调递减.
(2)要使不等式f(x)≥g(x)恒成立,即 -3≥aln x-2x恒成立,
即xex-aeln x+2ex-3e≥0恒成立,
令u(x)=xex-aeln x+2ex-3e,则u(1)=0,
要使得原不等式成立,则u(x)在x=1处取得最小值且是极小值,
因为u′(x)=
所以u′(1)=0可得a=4,
检验a=4时,u′(x)=
设v(x)=x(x+1)ex+2ex-4e,且v(1)=0,
显然v(x)在(0,+∞)上单调递增,
当x∈(0,1)时,v(x)<0,即u′(x)<0,u(x)单调递减,当x∈(1,+∞)时,v(x)>0,即u′(x)>0,u(x)单调递增,
故u(x)的最小值u(1)=0,满足题意,
综上,a=4.
同课章节目录
