等差数列与等比数列课件(共37张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 等差数列与等比数列课件(共37张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 547.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 20:32:10 | ||
图片预览






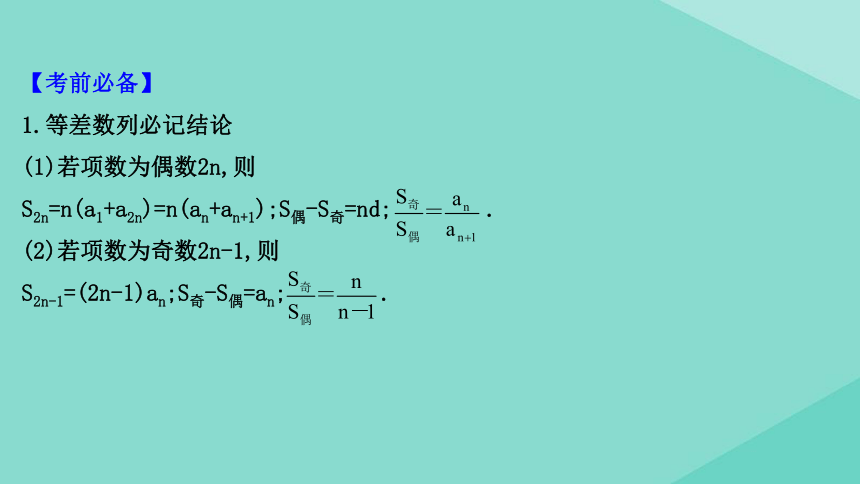




文档简介
(共37张PPT)
等差数列与等比数列
真题再研析·提升审题力
考向一 等差数列基本量的计算
【典例】
(2020·全国Ⅱ卷)记Sn为等差数列{an}的前n项和.若a1=-2,a2+a6=2①,则
=________.
【解析】设等差数列{an}的公差为d.
因为{an}是等差数列,且a1=-2,a2+a6=2,
根据等差数列通项公式:an=a1+(n-1)d,
可得a1+d+a1+5d=2,即-2+d+(-2)+5d=2,
整理可得:6d=6,解得:d=1.
根据等差数列前n项和公式:Sn=na1+
d,n∈N
,
可得:S10=10×(-2)+
=-20+45=25,
所以S10=25.
答案:25
【题眼直击】
①
根据基本量列方程
②
前n项和公式求解
考向二 等比数列基本量的计算
【典例】(2020·全国Ⅰ卷)设{an}是等比数列,且a1+a2+a3=1,a2+a3+a4=2,则a6+a7+a8=( )
A.12
B.24
C.30
D.32
D 设等比数列{an}的公比为q,
则a1+a2+a3=a1(1+q+q2)=1,
a2+a3+a4=a1q+a1q2+a1q3=a1q(1+q+q2)=q=2,
因此,a6+a7+a8=a1q5+a1q6+a1q7=a1q5(1+q+q2)=q5=32.
【考前必备】
1.等差数列必记结论
(1)若项数为偶数2n,则
S2n=n(a1+a2n)=n(an+an+1);S偶-S奇=nd;
.
(2)若项数为奇数2n-1,则
S2n-1=(2n-1)an;S奇-S偶=an;
.
2.等比数列必记结论
(1)ak,ak+m,ak+2m,…仍是等比数列,公比为qm(k,m∈N
).
(2)若数列{an}的项数为2n,则
=q;
(3)若项数为2n+1,则
=q.
【考场秘技】
1.数列中的方程思想
无论是等差数列中的a1,n,d,an,Sn,还是等比数列中的a1,n,q,an,Sn,一般可以“知三求二”,通过列方程(组)求关键量a1和d(q),问题可迎刃而解
2.数列中的函数思想
数列是一种特殊的函数,在研究数列问题时,既要注意函数方法的普遍性,又要考虑数列方法的特殊性.
【命题陷阱】
1.弄错首项致错
如T10中,数列{bn}的首项为b1,不是
.
2.忽略数列与函数的区别致错
如T13一定要注意自变量n是正整数.
3.忽略题目中的隐含条件而致错
如T11要注意b2的符号已经确定,且b2<0,忽视了这一隐含条件,就容易出现错误.
1.在公比为
的等比数列{an}中,若sin(a1a4)=
,则cos(a2a5)的值是
( )
A.-
B.
C.
D.
高考演兵场·检验考试力
B 由等比数列的通项公式可知:a2a5=(a1a4)q2=2(a1a4),
cos(a2a5)
=
1-2sin2(a1a4)=1-2×
=
.
2.数列{an}中,a1=2,a2=1,则
(n∈N
),则a10等于( )
A.-5
B.-
C.5
D.
D 因为
(n∈N
),所以
是等差数列,
又因为a1=2,a2=1,所以
,
所以
是首项为
,公差为
的等差数列,
所以
,所以a10=
.
3.若数列{xn}满足lg
xn+1=1+lg
xn(n∈N+),且x1+x2+x3+…+x100=100,则lg(x101+x102+…+x200)的值为
( )
A.102 B.101 C.100 D.99
A 由lg
xn+1=1+lg
xn,得
=10,所以数列{xn}是公比为10的等比数列,
又x101=x1·q100,x102=x2·q100,…,x200=x100·q100,
所以x101+x102+…+x200=q100(x1+x2+…+x100)=10100·100=10102,
所以lg(x101+x102+…+x200)=102.
4.我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是
( )
A.相邻两个节气晷长减少或增加的量为一尺
B.春分和秋分两个节气的晷长相同
C.立冬的晷长为一丈五寸
D.立春的晷长比立秋的晷长短
D 由题意可知夏至到冬至的晷长构成等差数列{an},其中a1=15寸,a13=135寸,
公差为d寸,则135=15+12d,解得d=10(寸),同理可知由冬至到夏至的晷长构成等差数列{bn},其中b1=135,b13=15,公差d=-10(单位都为寸).故选项A正确;因为春分的晷长为b7,所以b7=b1+6d=135-60=75,因为秋分的晷长为a7,所以a7=a1+6d=15+60=75,所以B正确;因为立冬的晷长为a10,所以a10=a1+9d=15+90=105,即立冬的晷长为一丈五寸,C正确;因为立春的晷长,立秋的晷长分别为b4,a4,所以a4=a1+3d=15+30=45,b4=b1+3d=135-30=105,所以b4>a4,故D错误.故选D.
5.数列
满足:an+1=λan-1
,若数列
是等比数列,则λ的
值是( )
A.1
B.2
C.
D.-1
B 数列
为等比数列?
=q,
即:λan-2=qan-q,由上式恒成立,可知:
?λ=2.
6.等比数列{an}中,a1=2,a8=4,函数f(x)=x(x-a1)(x-a2)·…·(x-a8),
则f′(0)=
( )
A.26
B.29
C.212
D.215
C f′(x)=[x(x-a1)(x-a2)·…·(x-a8)]′
=x′[(x-a1)(x-a2)·…·(x-a8)]+x[(x-a1)(x-a2)·…·(x-a8)]′
=[(x-a1)(x-a2)·…·(x-a8)]+x[(x-a1)(x-a2)·…·(x-a8)]′,
所以f′(0)=a1a2·…·a8,
又a1a8=a2a7=a3a6=a4a5,
所以f′(0)=(a1a8)4=84=212,故选C.
7.已知数阵
中,每行的三个数依次成等比数列,每列的三个数也依
次成等比数列,若a22=2,则该数阵中九个数的积为
( )
A.36
B.256
C.512
D.1
024
C 依题意可得a11a13=
,a21a23=
,a31a33=
,a12a32=
,
因为a22=2,
所以a11a12a13a21a22a23a31a32a33
=(a11a13)a12(a21a23)a22(a31a33)a32
=
=
=29=512.
8.已知数列{an}是等比数列,数列{bn}是等差数列,若a1·a6·a11=-3
,
b1+b6+b11=7π,则tan
的值是
( )
A.1
B.
C.-
D.-
D 在等差数列{bn}中,由b1+b6+b11=7π,得3b6=7π,b6=
,所以b3+b9=2b6=
,
在等比数列{an}中,由a1a6a11=-3
,得
=-3
,a6=-
,
所以1-a4a8=1-
=1-(-
)2=-2,
则
.
9.已知每项均大于零的数列{an}中,首项a1=1且前n项和Sn满足
=
(n∈N
且n≥2),则a81=
( )
A.641
B.640
C.639
D.638
B 因为Sn
-Sn-1
=
,所以
-
=2,即{
}为等差数列,
首项为1,公差为2,所以
=1+2(n-1)=2n-1所以Sn=(2n-1)2,
因此a81=S81-S80=1612-1592=640.
10.若数列{bn}满足:
,则数列{bn}的前n项和Sn为
( )
A.2n+1 B.2n-4
C.2n+2-2
D.2n+2-4
D 对任意的n∈N
,
.
当n=1时,
=2,可得b1=4;
当n≥2时,由
=2n,
可得
=2(n-1),
两式相减得
=2,所以bn=2n+1.
又b1=4符合bn=2n+1,所以bn=2n+1(n∈N
),
所以
=2,所以,数列{bn}为等比数列,且公比为2,首项b1=4,
因此,Sn=
=2n+2-4.
11.已知数列-1,a1,a2,-4成等差数列,-1,b1,b2,b3,-4成等比数列,
则
=________
【解析】因为-1,a1,a2,-4成等差数列,设公差为d,则a2-a1=d=
[(-4)-(-1)]
=-1,因为-1,b1,b2,b3,-4成等比数列,所以
=(-1)×(-4)=4,所以b2=±2.若设公
比为q,则b2=(-1)q2,所以b2<0.所以b2=-2,所以
.
答案:
12.已知数列
满足a1=2,
=2,若bn=
,则数列
的前n项和Sn=____.?
【解析】由题意知
为公差是2的等差数列,所以
+(n-1)×2=2n,所以
an=2n2,所以bn=22n,所以Sn=
.
答案:
13.已知数列
满足a1=1,an=
(n≥2),当n≥2时,bn=n,且点
是直线
y=x+1上的点,则数列
的通项公式为__________;令y=?a1·a2·a3·…·ak,
则当k在区间[1,2019]内时,使y的值为正整数的所有k值之和为________.
【解析】因为当n≥2时,bn=n,且点
是直线y=x+1上的点,所以当n≥2时,
有an=logn(n+1)(n≥2),所以an=
所以y=1×log23×log34×…×logk(k+1)
=1×
=log2(k+1),
令log2(k+1)=m得k+1=2m,所以k=2m-1,
所以当k在[1,2
019]内时,即1≤2m-1≤2
019,得1≤m≤10,m∈N
,
所以使y的值为正整数的所有k值之和为
答案:an=
2
036
等差数列与等比数列
真题再研析·提升审题力
考向一 等差数列基本量的计算
【典例】
(2020·全国Ⅱ卷)记Sn为等差数列{an}的前n项和.若a1=-2,a2+a6=2①,则
=________.
【解析】设等差数列{an}的公差为d.
因为{an}是等差数列,且a1=-2,a2+a6=2,
根据等差数列通项公式:an=a1+(n-1)d,
可得a1+d+a1+5d=2,即-2+d+(-2)+5d=2,
整理可得:6d=6,解得:d=1.
根据等差数列前n项和公式:Sn=na1+
d,n∈N
,
可得:S10=10×(-2)+
=-20+45=25,
所以S10=25.
答案:25
【题眼直击】
①
根据基本量列方程
②
前n项和公式求解
考向二 等比数列基本量的计算
【典例】(2020·全国Ⅰ卷)设{an}是等比数列,且a1+a2+a3=1,a2+a3+a4=2,则a6+a7+a8=( )
A.12
B.24
C.30
D.32
D 设等比数列{an}的公比为q,
则a1+a2+a3=a1(1+q+q2)=1,
a2+a3+a4=a1q+a1q2+a1q3=a1q(1+q+q2)=q=2,
因此,a6+a7+a8=a1q5+a1q6+a1q7=a1q5(1+q+q2)=q5=32.
【考前必备】
1.等差数列必记结论
(1)若项数为偶数2n,则
S2n=n(a1+a2n)=n(an+an+1);S偶-S奇=nd;
.
(2)若项数为奇数2n-1,则
S2n-1=(2n-1)an;S奇-S偶=an;
.
2.等比数列必记结论
(1)ak,ak+m,ak+2m,…仍是等比数列,公比为qm(k,m∈N
).
(2)若数列{an}的项数为2n,则
=q;
(3)若项数为2n+1,则
=q.
【考场秘技】
1.数列中的方程思想
无论是等差数列中的a1,n,d,an,Sn,还是等比数列中的a1,n,q,an,Sn,一般可以“知三求二”,通过列方程(组)求关键量a1和d(q),问题可迎刃而解
2.数列中的函数思想
数列是一种特殊的函数,在研究数列问题时,既要注意函数方法的普遍性,又要考虑数列方法的特殊性.
【命题陷阱】
1.弄错首项致错
如T10中,数列{bn}的首项为b1,不是
.
2.忽略数列与函数的区别致错
如T13一定要注意自变量n是正整数.
3.忽略题目中的隐含条件而致错
如T11要注意b2的符号已经确定,且b2<0,忽视了这一隐含条件,就容易出现错误.
1.在公比为
的等比数列{an}中,若sin(a1a4)=
,则cos(a2a5)的值是
( )
A.-
B.
C.
D.
高考演兵场·检验考试力
B 由等比数列的通项公式可知:a2a5=(a1a4)q2=2(a1a4),
cos(a2a5)
=
1-2sin2(a1a4)=1-2×
=
.
2.数列{an}中,a1=2,a2=1,则
(n∈N
),则a10等于( )
A.-5
B.-
C.5
D.
D 因为
(n∈N
),所以
是等差数列,
又因为a1=2,a2=1,所以
,
所以
是首项为
,公差为
的等差数列,
所以
,所以a10=
.
3.若数列{xn}满足lg
xn+1=1+lg
xn(n∈N+),且x1+x2+x3+…+x100=100,则lg(x101+x102+…+x200)的值为
( )
A.102 B.101 C.100 D.99
A 由lg
xn+1=1+lg
xn,得
=10,所以数列{xn}是公比为10的等比数列,
又x101=x1·q100,x102=x2·q100,…,x200=x100·q100,
所以x101+x102+…+x200=q100(x1+x2+…+x100)=10100·100=10102,
所以lg(x101+x102+…+x200)=102.
4.我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是
( )
A.相邻两个节气晷长减少或增加的量为一尺
B.春分和秋分两个节气的晷长相同
C.立冬的晷长为一丈五寸
D.立春的晷长比立秋的晷长短
D 由题意可知夏至到冬至的晷长构成等差数列{an},其中a1=15寸,a13=135寸,
公差为d寸,则135=15+12d,解得d=10(寸),同理可知由冬至到夏至的晷长构成等差数列{bn},其中b1=135,b13=15,公差d=-10(单位都为寸).故选项A正确;因为春分的晷长为b7,所以b7=b1+6d=135-60=75,因为秋分的晷长为a7,所以a7=a1+6d=15+60=75,所以B正确;因为立冬的晷长为a10,所以a10=a1+9d=15+90=105,即立冬的晷长为一丈五寸,C正确;因为立春的晷长,立秋的晷长分别为b4,a4,所以a4=a1+3d=15+30=45,b4=b1+3d=135-30=105,所以b4>a4,故D错误.故选D.
5.数列
满足:an+1=λan-1
,若数列
是等比数列,则λ的
值是( )
A.1
B.2
C.
D.-1
B 数列
为等比数列?
=q,
即:λan-2=qan-q,由上式恒成立,可知:
?λ=2.
6.等比数列{an}中,a1=2,a8=4,函数f(x)=x(x-a1)(x-a2)·…·(x-a8),
则f′(0)=
( )
A.26
B.29
C.212
D.215
C f′(x)=[x(x-a1)(x-a2)·…·(x-a8)]′
=x′[(x-a1)(x-a2)·…·(x-a8)]+x[(x-a1)(x-a2)·…·(x-a8)]′
=[(x-a1)(x-a2)·…·(x-a8)]+x[(x-a1)(x-a2)·…·(x-a8)]′,
所以f′(0)=a1a2·…·a8,
又a1a8=a2a7=a3a6=a4a5,
所以f′(0)=(a1a8)4=84=212,故选C.
7.已知数阵
中,每行的三个数依次成等比数列,每列的三个数也依
次成等比数列,若a22=2,则该数阵中九个数的积为
( )
A.36
B.256
C.512
D.1
024
C 依题意可得a11a13=
,a21a23=
,a31a33=
,a12a32=
,
因为a22=2,
所以a11a12a13a21a22a23a31a32a33
=(a11a13)a12(a21a23)a22(a31a33)a32
=
=
=29=512.
8.已知数列{an}是等比数列,数列{bn}是等差数列,若a1·a6·a11=-3
,
b1+b6+b11=7π,则tan
的值是
( )
A.1
B.
C.-
D.-
D 在等差数列{bn}中,由b1+b6+b11=7π,得3b6=7π,b6=
,所以b3+b9=2b6=
,
在等比数列{an}中,由a1a6a11=-3
,得
=-3
,a6=-
,
所以1-a4a8=1-
=1-(-
)2=-2,
则
.
9.已知每项均大于零的数列{an}中,首项a1=1且前n项和Sn满足
=
(n∈N
且n≥2),则a81=
( )
A.641
B.640
C.639
D.638
B 因为Sn
-Sn-1
=
,所以
-
=2,即{
}为等差数列,
首项为1,公差为2,所以
=1+2(n-1)=2n-1所以Sn=(2n-1)2,
因此a81=S81-S80=1612-1592=640.
10.若数列{bn}满足:
,则数列{bn}的前n项和Sn为
( )
A.2n+1 B.2n-4
C.2n+2-2
D.2n+2-4
D 对任意的n∈N
,
.
当n=1时,
=2,可得b1=4;
当n≥2时,由
=2n,
可得
=2(n-1),
两式相减得
=2,所以bn=2n+1.
又b1=4符合bn=2n+1,所以bn=2n+1(n∈N
),
所以
=2,所以,数列{bn}为等比数列,且公比为2,首项b1=4,
因此,Sn=
=2n+2-4.
11.已知数列-1,a1,a2,-4成等差数列,-1,b1,b2,b3,-4成等比数列,
则
=________
【解析】因为-1,a1,a2,-4成等差数列,设公差为d,则a2-a1=d=
[(-4)-(-1)]
=-1,因为-1,b1,b2,b3,-4成等比数列,所以
=(-1)×(-4)=4,所以b2=±2.若设公
比为q,则b2=(-1)q2,所以b2<0.所以b2=-2,所以
.
答案:
12.已知数列
满足a1=2,
=2,若bn=
,则数列
的前n项和Sn=____.?
【解析】由题意知
为公差是2的等差数列,所以
+(n-1)×2=2n,所以
an=2n2,所以bn=22n,所以Sn=
.
答案:
13.已知数列
满足a1=1,an=
(n≥2),当n≥2时,bn=n,且点
是直线
y=x+1上的点,则数列
的通项公式为__________;令y=?a1·a2·a3·…·ak,
则当k在区间[1,2019]内时,使y的值为正整数的所有k值之和为________.
【解析】因为当n≥2时,bn=n,且点
是直线y=x+1上的点,所以当n≥2时,
有an=logn(n+1)(n≥2),所以an=
所以y=1×log23×log34×…×logk(k+1)
=1×
=log2(k+1),
令log2(k+1)=m得k+1=2m,所以k=2m-1,
所以当k在[1,2
019]内时,即1≤2m-1≤2
019,得1≤m≤10,m∈N
,
所以使y的值为正整数的所有k值之和为
答案:an=
2
036
同课章节目录
