函数的图象及性质课件(共65张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 函数的图象及性质课件(共65张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 792.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 20:32:30 | ||
图片预览











文档简介
(共65张PPT)
函数的图象及性质
真题再研析·提升审题力
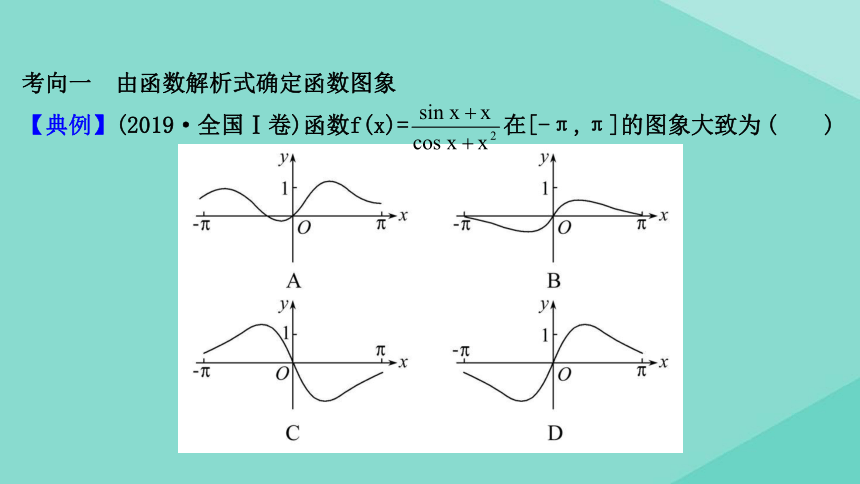
考向一 由函数解析式确定函数图象
【典例】(2019·全国Ⅰ卷)函数f(x)=
在[-π,π]的图象大致为
( )
D 由f(-x)=
=-f(x),
得f(x)是奇函数,其图象关于原点对称.
又
>1,f(π)=
>0.故选D.
考向二 函数基本性质的综合应用
【典例】(2020·全国Ⅱ卷)设函数f(x)=x3-
,则f(x)
( )
A.是奇函数①,且在(0,+∞)单调递增②
B.是奇函数,且在(0,+∞)单调递减
C.是偶函数,且在(0,+∞)单调递增
D.是偶函数,且在(0,+∞)单调递减
A 因为函数f(x)=x3-
的定义域为
,其关于原点对称,
而f(-x)=-f(x),所以函数f(x)为奇函数.
又因为函数y=x3在(0,+∞)上单调递增,
在(-∞,0)上单调递增,
而y=
=x-3在(0,+∞)上单调递减,
在(-∞,0)上单调递减,
所以函数f(x)=x3-
在(0,+∞)上单调递增,
在(-∞,0)上单调递增.
【题眼直击】
①
利用定义f(-x)=-f(x)
②
利用复合函数同增异减
【考前必备】
1.知式选图的四个切入点
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;
(2)从函数的单调性,判断图象的变化趋势;
(3)从函数的奇偶性,判断图象的对称性;
(4)从函数的周期性,判断图象的循环往复.
2.对称性的三个常用结论
(1)若函数y=f(x+a)是偶函数,则函数y=f(x)的图象关于直线x=a对称.
(2)若对于R上的任意x都有f(2a-x)=f(x)或f(-x)=f(2a+x),则y=f(x)的图象关于直线x=a对称.
(3)若函数y=f(x+b)是奇函数,则函数y=f(x)的图象关于点(b,0)中心对称.
【考场秘技】
1.确定函数图象的方法
(1)奇偶性定对称
(2)特殊值定正负
(3)端点值定趋势
2.图象对称巧变换
(1)y=f(x)
y=|f(x)|.
(2)y=f(x)
y=f(|x|).
3.恒成立(有解)问题巧转化
若f(x)≤m
在x∈[a,b]恒成立,则等价于f(x)max≤m
;
若f(x)≤m
在x∈[a,b]有解,则使f(x)min≤m.
【命题陷阱】
1.分段函数的单调性,除注意各段的单调性外,还要注意衔接点的取值.
【案例】T19要考虑x=1时满足1-2a+3a≥0.
2.用换元法求函数的值域,要注意换元后自变量的取值范围也会发生变化.
【案例】T25原函数自变量x的取值范围是R,换元后t=
>0,而不是t∈R.
3.切记弄清有解和恒成立的区别
【案例】T28将不等式进行化简得mx2+2上有解.本题易错点是,误将
m<
在区间[1,5]上有解当成m<
.勿将恒成立问题和不等式在区间上
有解问题混淆.
1.已知函数f(x)=
若f(f(0))=1,则a的值为
( )
A.1 B.0 C.-1 D.2
A f(f(0))=f(-e0)=f(-1)=a(-1)2=1,
所以a的值为1.
高考演兵场·检验考试力
2.已知函数f(x)=loga(ax+1)+
x(a>0且a≠1),则
( )
A.f(x)图象关于原点对称
B.f(x)图象关于y轴对称
C.f(x)在R上单调递增
D.f(x)在R上单调递减
C 因为f(x)+
≠0,f(x)-
≠0,可知f(x)为非奇非偶函数,故排除A,B.
当a>1时,u=ax+1在R上单调递增,y=logat在
上单调递增,且y=
x在R上单调
递增,所以f(x)在R上单调递增,当0上单调递减,且y=
x在R上单调递增,所以f(x)在R上单调递增,故选C.
3.定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞),有
<0,则
对任意的n>1,下列各式成立的是
( )
A.f(n+1)B.f(n-1)C.f(-n)D.f(n+1)A 由对任意的x1,x2∈[0,+∞),有
<0,
可得f(x)在[0,+∞)上单调递减,再由f(x)为偶函数,
则f(-n)=f(n),又n+1>n>n-1>0,
则f(n+1)4.已知函数f(x)=ax3-
+1,则f(lg3)+f(lg
)的值等于
( )
A.2 B.1 C.3 D.9
A f(x)-1=ax3-
是奇函数,
所以
-1+f(x)-1=0,
即
+f(x)=2,
所以
.
5.如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是
( )
C 如图,把函数y=log2x的图象向左平移一个单位得到y=log2(x+1)的图象,在
x=1时,两图象相交,由图知不等式的解为-1.
6.函数f(x)=
cos
x图象的大致形状是
( )
B f(x)=
,
,
故f(x)为奇函数,排除选项A,C;
又f(1)=
cos
1<0,排除D,故选B.
7.已知函数f(x)=e|x|-e-|x|,则f(x)
( )
A.是奇函数,且在(0,+∞)上单调递增
B.是奇函数,且在(0,+∞)上单调递减
C.是偶函数,且在(0,+∞)上单调递增
D.是偶函数,且在(0,+∞)上单调递减
C 函数f(x)=
e|x|-e-|x|的定义域为R,f(-x)=e|-x|-e-|x|=e|x|-e-|x|=f(x),即
f(-x)=f(x),所以f(x)
是偶函数,当x>0时,f(x)=ex-e-x,y=ex为增函数,y=e-x为
减函数,所以f(x)在(0,+∞)上单调递增,故选C.
8.1614年纳皮尔在研究天文学的过程中为了简化计算而发明对数;1637年笛卡尔
开始使用指数运算;1770年,欧拉发现了指数与对数的互逆关系,指出:对数源于
指数,对数的发明先于指数,称为历史上的珍闻.若2x=
,lg2≈0.301
0,则x的值
约为
( )
A.1.322 B.1.410 C.1.507 D.1.669
A 因为2x=
,所以x=log2
=
≈1.322.
9.定义在R上的奇函数f(x)满足f(x+1)=f(1-x),且x∈[0,1]时,f(x)=2x-1,
则f(log2
8)=
( )
A.-1
B.1
C.7
D.-
A 因为f(x+1)=f(1-x),所以f(log28)=f(3)=f(-1),又f(x)是奇函数,
且x∈
时,f(x)=2x-1,所以f(-1)=-f(1)=-21+1=-1,所以f(log28)=-1.
10.已知函数f(x)=|x-m|与函数g(x)的图象关于y轴对称.若g(x)在区间(1,2)内单调递减,则m的取值范围为
( )
A.[-1,+∞)
B.(-∞,-1]
C.[-2,+∞)
D.(-∞,-2]
D 函数f(x)=|x-m|与函数g(x)的图象关于y轴对称,
所以g(x)=f(-x)=|x+m|,
g(x)在区间(1,2)内单调递减,
则-m≥2,
所以m≤-2.
11.下列图象可以作为函数f(x)=
的图象的有
( )
A.1个
B.2个
C.3个
D.4个
C 当a<0时,如取a=-4,则f(x)=
,其定义域为:{x|x≠±2},它是奇函数,图
象是③,所以③符合题意;当a>0时,如取a=1,其定义域为R,它是奇函数,图象是②.
所以②符合题意;当a=0时,则f(x)=
,其定义域为:{x|x≠0},它是奇函数,图象
是④,所以④符合题意.
12.已知函数f(x)是定义在R上的奇函数,当x∈[0,1]时,f(x)单调递减,且满足f(1+x)=f(1-x),则
( )
A.f(1)B.f(2)C.f(3)D.f(1)A 因为函数f(x)是定义域为R的奇函数,所以f(0)=0,
因为当x∈[0,1]时,f(x)单调递减,所以f(x)在x∈[-1,1]单调递减,
因为f(1+x)=f(1-x),所以函数f(x)的图象关于直线x=1对称,
所以f(x)在x∈[1,3]单调递增,
所以f(1)13.若f(x)是R上周期为3的奇函数,且当0时,f(x)=
+log2x,
则f(5)+f(-
)=
( )
A.
B.-
C.
-2
D.2-
B 因为f(x)是R上周期为3的奇函数,
所以f(5)=f(2)=f(-1)=-f(1)=-(
+log21)=-1,
.
所以f(5)+
.
14.已知函数f(x)=
的最大值为M,最小值为m,则M+m的值为
( )
A.0
B.1
C.2
D.3
C 因为f(x)=
=
,令g(x)=
,
则
,所以函数g(x)=
为奇函数,
又函数f(x)=
的最大值为M,最小值为m,
所以M+m=f(x)max+f(x)min=1-g(x)min+1-g(x)max=
.
15.当0时,16x( )
B 当a>1时,16x∈
[1,2],logax<0
,不成立,当0当x=
时,令
=loga
,解得:a=
,
如图,若x∈
,16x≤a<1.
16.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-3x,则函数
g(x)=f(x)-x+3
的零点的集合为
( )
D ①当x≥0时,f(x)=x2-3x,令g(x)=f(x)-x+3=x2-3x-x+3=x2-4x+3=0,
解得x=1或3,
②设x<0,则-x>0,则f(x)=-f(-x)=-[(-x)2-3(-x)]=-x2-3x,
令g(x)=f(x)-x+3=-x2-3x-x+3=0,所以-x2-4x+3=0,
所以x2+4x-3=0,所以(x+2)2=7,所以x=-2-
(正值舍去).
17.函数y=
的定义域是________.?
【解析】由题意可知:
?0答案:
(0,7)
18.已知幂函数f(x)=
为偶函数,且在区间(0,+∞)上是单调增函数,则f(2)的值为________.?
【解析】因为幂函数f(x)在区间(0,+∞)上是单调增函数,
所以-m2-2m+3>0,解得:-3因为m∈Z,所以m=-2或-1或0.
因为幂函数f(x)为偶函数,所以-m2-2m+3是偶数,
当m=-2时,-m2-2m+3=3,不符合,舍去;
当m=-1时,-m2-2m+3=4;
当m=0时,-m2-2m+3=3,不符合,舍去.
所以f(x)=x4,故f(2)=24=16.
答案:16
19.已知函数f(x)=
的值域为R,则实数a的取值范围是_______.
【解析】由题意知y=ln
x(x≥1)的值域为[0,+∞),
故要使f(x)的值域为R,则必有y=(1-2a)x+3a为增函数,
且1-2a+3a≥0,所以1-2a>0且a≥-1,解得-1≤a<
,
实数a的取值范围是
.
答案:
20.如果二次函数f(x)=x2-(a-1)x+5在区间(
,1)上是增函数,则实数a的取值范
围为________.?
【解析】因为函数f(x)=x2-(a-1)x+5的对称轴为直线x=
且在区间
上是增函数,
所以
≤
,即a≤2.
故实数a的取值范围为(-∞,2].
答案:(-∞,2]
21.某部影片的盈利额(即影片的票房收入与固定成本之差)记为y,观影人数记为x,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后y与x的函数图象.
给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是________.(填写所有正确说法的编号)?
【解析】由图象(1)可设盈利额y与观影人数x的函数为y=kx+b,k>0,b<0,即k为票价,当k=0时,y=b,则-b为固定成本,由图象(2)知,直线向上平移,k不变,即票价不变,b变大,则-b变小,成本减小.故①错误,②正确;由图象(3)知,直线与y轴的交点不变,直线斜率变大,k变大,即提高票价,
b不变,则-b不变,成本不变.故③正确,④错误;
答案:②③
22.如图所示为函数在区间(-1,2]上的图象,则此函数的解析式f(x)=________.?
【解析】由图象可知,每一段都是一次函数,设f(x)=kx+b,k≠0,当x∈(-1,0)时,
直线过点(-1,0),(0,1),所以
,所以f(x)=x+1,当x∈[0,2]时,直线过点
(0,0),(2,-1),所以
,解得
,所以f(x)=-
x,
所以f(x)=
答案:
23.当生物死亡后,它机体内原有的碳14会按确定的规律衰减.大约每经过5
730
年衰减为原来的一半,这个时间称为“半衰期”.当死亡生物组织内的碳14的含
量不足死亡前的千分之一时,用一般的放射性探测器就测不到碳14了.如果用一
般的放射性探测器不能测到碳14,那么死亡生物组织内的碳14至少经过了
________个“半衰期”.(提示:
≈0.001
95)?
【解析】设生物组织内原有的碳14含量为x,
需要经过n个“半衰期”才不能测到碳14,
则x·
<
x,即
<0.001,
由参考数据可知,
≈0.001
95>0.001,
≈0.001
95×
=0.000
975<0.001,所以n=10.
答案:10
24.使log2(-x)【解析】在同一坐标系中分别画出函数y=log2(-x)和y=x+1的图象(如图所示),由图象,得使log2(-1)<
x+1成立的x的取值范围是(-1,0).
答案:(-1,0)
25.函数y=
+
+1的值域为________.
25.【解析】令t=
,t∈(0,+∞),则原函数可化为y=t2+t+1=
,因为
函数y=
在(0,+∞)是增函数,所以y>
=1,即原函数的值域是
(1,+∞).
答案:(1,+∞)
26.已知偶函数y=f(x)(x∈R)在区间[-1,0]上单调递增,且满足f(1-x)+f(1+x)=0,给出下列判断:
①f(5)=0;
②f(x)在[1,2]上是减函数;
③函数f(x)没有最小值;
④函数f(x)在x=0处取得最大值;
⑤f(x)的图象关于直线x=1对称.
其中判断正确的序号是________.?
26.【解析】因为f(1-x)+f(1+x)=0,
所以f(1+x)=-f(1-x)=-f
,
所以f(2+x)=-f(x),所以f(x+4)=f(x),即函数f(x)是周期为4的周期函数.
由题意知,函数y=f(x)
关于点
对称,画出满足条件的图象如图所示,
结合图象可知①②④正确.
答案:①②④
27.函数f(x)的定义域为[-1,1),其图象如图所示.函数g(x)是定义域为R的奇函数,满足g(2-x)+g(x)=0,且当x∈(0,1)时,g(x)=f(x).给出下列三个结论:
①g(0)=0;②函数g(x)在(-1,5)内有且仅有3个零点;③不等式f(-x)<0的解集为{x|-1其中,正确结论的序号是________.?
27.【解析】因为函数y=g(x)是奇函数,所以g(x)=-g(-x),
又g(2-x)+g(x)=0,所以g(2-x)=g(-x),即g(x+2)=g(x),
所以,函数y=g(x)的周期为2.
对于①,由于函数y=g(x)是R上的奇函数,
所以,g(0)=0,故①正确;
对于②,因为g(2-x)+g(x)=0,令x=1,可得2g(1)=0,得g(1)=0,
所以,函数y=g(x)在区间(-1,1]上的零点为0和1.
因为函数y=g(x)的周期为2,
所以函数y=g(x)在(-1,5)内有5个零点,分别是0,1,2,3,4,故②错误;
对于③,令t=-x,则需求f(t)<0的解集,
由图象可知,0答案:①③
28.已知函数f(x)=x3+x,若关于x的不等式f(mx2+2)
+f(-x)<0在区间[1,5]上有解,则实数m的取值范围为________.?
【解析】由f(x)=x3+x知,f′(x)=3x2+1>0
,所以f(x)在R上单调递增;因为
f(-x)=-x3-x=-f(x)
且函数定义域为R,所以f(x)
为奇函数,则f(mx2+2)+f(-x)<0
即为f(mx2+2)<-f(-x)=f(x),由函数单调递增可知,mx2+2即m<
在区间[1,5]上有解,只需m<
,令g(x)=
,x∈[1,5],则
g′(x)=
,令g′(x)=0,解得x=4
,因为当x∈[1,4)时,g′(x)=
>0,
则g(x)在x∈[1,4)单调递增;当x∈[4,5]时,g′(x)=
<0,则g(x)在x∈[4,5]
单调递减.所以,当x=4
时,g(x)有最大值为g(4)=
,故m<
.
答案:m<
函数的图象及性质
真题再研析·提升审题力
考向一 由函数解析式确定函数图象
【典例】(2019·全国Ⅰ卷)函数f(x)=
在[-π,π]的图象大致为
( )
D 由f(-x)=
=-f(x),
得f(x)是奇函数,其图象关于原点对称.
又
>1,f(π)=
>0.故选D.
考向二 函数基本性质的综合应用
【典例】(2020·全国Ⅱ卷)设函数f(x)=x3-
,则f(x)
( )
A.是奇函数①,且在(0,+∞)单调递增②
B.是奇函数,且在(0,+∞)单调递减
C.是偶函数,且在(0,+∞)单调递增
D.是偶函数,且在(0,+∞)单调递减
A 因为函数f(x)=x3-
的定义域为
,其关于原点对称,
而f(-x)=-f(x),所以函数f(x)为奇函数.
又因为函数y=x3在(0,+∞)上单调递增,
在(-∞,0)上单调递增,
而y=
=x-3在(0,+∞)上单调递减,
在(-∞,0)上单调递减,
所以函数f(x)=x3-
在(0,+∞)上单调递增,
在(-∞,0)上单调递增.
【题眼直击】
①
利用定义f(-x)=-f(x)
②
利用复合函数同增异减
【考前必备】
1.知式选图的四个切入点
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;
(2)从函数的单调性,判断图象的变化趋势;
(3)从函数的奇偶性,判断图象的对称性;
(4)从函数的周期性,判断图象的循环往复.
2.对称性的三个常用结论
(1)若函数y=f(x+a)是偶函数,则函数y=f(x)的图象关于直线x=a对称.
(2)若对于R上的任意x都有f(2a-x)=f(x)或f(-x)=f(2a+x),则y=f(x)的图象关于直线x=a对称.
(3)若函数y=f(x+b)是奇函数,则函数y=f(x)的图象关于点(b,0)中心对称.
【考场秘技】
1.确定函数图象的方法
(1)奇偶性定对称
(2)特殊值定正负
(3)端点值定趋势
2.图象对称巧变换
(1)y=f(x)
y=|f(x)|.
(2)y=f(x)
y=f(|x|).
3.恒成立(有解)问题巧转化
若f(x)≤m
在x∈[a,b]恒成立,则等价于f(x)max≤m
;
若f(x)≤m
在x∈[a,b]有解,则使f(x)min≤m.
【命题陷阱】
1.分段函数的单调性,除注意各段的单调性外,还要注意衔接点的取值.
【案例】T19要考虑x=1时满足1-2a+3a≥0.
2.用换元法求函数的值域,要注意换元后自变量的取值范围也会发生变化.
【案例】T25原函数自变量x的取值范围是R,换元后t=
>0,而不是t∈R.
3.切记弄清有解和恒成立的区别
【案例】T28将不等式进行化简得mx2+2
m<
在区间[1,5]上有解当成m<
.勿将恒成立问题和不等式在区间上
有解问题混淆.
1.已知函数f(x)=
若f(f(0))=1,则a的值为
( )
A.1 B.0 C.-1 D.2
A f(f(0))=f(-e0)=f(-1)=a(-1)2=1,
所以a的值为1.
高考演兵场·检验考试力
2.已知函数f(x)=loga(ax+1)+
x(a>0且a≠1),则
( )
A.f(x)图象关于原点对称
B.f(x)图象关于y轴对称
C.f(x)在R上单调递增
D.f(x)在R上单调递减
C 因为f(x)+
≠0,f(x)-
≠0,可知f(x)为非奇非偶函数,故排除A,B.
当a>1时,u=ax+1在R上单调递增,y=logat在
上单调递增,且y=
x在R上单调
递增,所以f(x)在R上单调递增,当0
x在R上单调递增,所以f(x)在R上单调递增,故选C.
3.定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞),有
<0,则
对任意的n>1,下列各式成立的是
( )
A.f(n+1)
<0,
可得f(x)在[0,+∞)上单调递减,再由f(x)为偶函数,
则f(-n)=f(n),又n+1>n>n-1>0,
则f(n+1)
+1,则f(lg3)+f(lg
)的值等于
( )
A.2 B.1 C.3 D.9
A f(x)-1=ax3-
是奇函数,
所以
-1+f(x)-1=0,
即
+f(x)=2,
所以
.
5.如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是
( )
C 如图,把函数y=log2x的图象向左平移一个单位得到y=log2(x+1)的图象,在
x=1时,两图象相交,由图知不等式的解为-1
6.函数f(x)=
cos
x图象的大致形状是
( )
B f(x)=
,
,
故f(x)为奇函数,排除选项A,C;
又f(1)=
cos
1<0,排除D,故选B.
7.已知函数f(x)=e|x|-e-|x|,则f(x)
( )
A.是奇函数,且在(0,+∞)上单调递增
B.是奇函数,且在(0,+∞)上单调递减
C.是偶函数,且在(0,+∞)上单调递增
D.是偶函数,且在(0,+∞)上单调递减
C 函数f(x)=
e|x|-e-|x|的定义域为R,f(-x)=e|-x|-e-|x|=e|x|-e-|x|=f(x),即
f(-x)=f(x),所以f(x)
是偶函数,当x>0时,f(x)=ex-e-x,y=ex为增函数,y=e-x为
减函数,所以f(x)在(0,+∞)上单调递增,故选C.
8.1614年纳皮尔在研究天文学的过程中为了简化计算而发明对数;1637年笛卡尔
开始使用指数运算;1770年,欧拉发现了指数与对数的互逆关系,指出:对数源于
指数,对数的发明先于指数,称为历史上的珍闻.若2x=
,lg2≈0.301
0,则x的值
约为
( )
A.1.322 B.1.410 C.1.507 D.1.669
A 因为2x=
,所以x=log2
=
≈1.322.
9.定义在R上的奇函数f(x)满足f(x+1)=f(1-x),且x∈[0,1]时,f(x)=2x-1,
则f(log2
8)=
( )
A.-1
B.1
C.7
D.-
A 因为f(x+1)=f(1-x),所以f(log28)=f(3)=f(-1),又f(x)是奇函数,
且x∈
时,f(x)=2x-1,所以f(-1)=-f(1)=-21+1=-1,所以f(log28)=-1.
10.已知函数f(x)=|x-m|与函数g(x)的图象关于y轴对称.若g(x)在区间(1,2)内单调递减,则m的取值范围为
( )
A.[-1,+∞)
B.(-∞,-1]
C.[-2,+∞)
D.(-∞,-2]
D 函数f(x)=|x-m|与函数g(x)的图象关于y轴对称,
所以g(x)=f(-x)=|x+m|,
g(x)在区间(1,2)内单调递减,
则-m≥2,
所以m≤-2.
11.下列图象可以作为函数f(x)=
的图象的有
( )
A.1个
B.2个
C.3个
D.4个
C 当a<0时,如取a=-4,则f(x)=
,其定义域为:{x|x≠±2},它是奇函数,图
象是③,所以③符合题意;当a>0时,如取a=1,其定义域为R,它是奇函数,图象是②.
所以②符合题意;当a=0时,则f(x)=
,其定义域为:{x|x≠0},它是奇函数,图象
是④,所以④符合题意.
12.已知函数f(x)是定义在R上的奇函数,当x∈[0,1]时,f(x)单调递减,且满足f(1+x)=f(1-x),则
( )
A.f(1)
因为当x∈[0,1]时,f(x)单调递减,所以f(x)在x∈[-1,1]单调递减,
因为f(1+x)=f(1-x),所以函数f(x)的图象关于直线x=1对称,
所以f(x)在x∈[1,3]单调递增,
所以f(1)
+log2x,
则f(5)+f(-
)=
( )
A.
B.-
C.
-2
D.2-
B 因为f(x)是R上周期为3的奇函数,
所以f(5)=f(2)=f(-1)=-f(1)=-(
+log21)=-1,
.
所以f(5)+
.
14.已知函数f(x)=
的最大值为M,最小值为m,则M+m的值为
( )
A.0
B.1
C.2
D.3
C 因为f(x)=
=
,令g(x)=
,
则
,所以函数g(x)=
为奇函数,
又函数f(x)=
的最大值为M,最小值为m,
所以M+m=f(x)max+f(x)min=1-g(x)min+1-g(x)max=
.
15.当0
B 当a>1时,16x∈
[1,2],logax<0
,不成立,当0
时,令
=loga
,解得:a=
,
如图,若x∈
,16x
16.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-3x,则函数
g(x)=f(x)-x+3
的零点的集合为
( )
D ①当x≥0时,f(x)=x2-3x,令g(x)=f(x)-x+3=x2-3x-x+3=x2-4x+3=0,
解得x=1或3,
②设x<0,则-x>0,则f(x)=-f(-x)=-[(-x)2-3(-x)]=-x2-3x,
令g(x)=f(x)-x+3=-x2-3x-x+3=0,所以-x2-4x+3=0,
所以x2+4x-3=0,所以(x+2)2=7,所以x=-2-
(正值舍去).
17.函数y=
的定义域是________.?
【解析】由题意可知:
?0
(0,7)
18.已知幂函数f(x)=
为偶函数,且在区间(0,+∞)上是单调增函数,则f(2)的值为________.?
【解析】因为幂函数f(x)在区间(0,+∞)上是单调增函数,
所以-m2-2m+3>0,解得:-3
因为幂函数f(x)为偶函数,所以-m2-2m+3是偶数,
当m=-2时,-m2-2m+3=3,不符合,舍去;
当m=-1时,-m2-2m+3=4;
当m=0时,-m2-2m+3=3,不符合,舍去.
所以f(x)=x4,故f(2)=24=16.
答案:16
19.已知函数f(x)=
的值域为R,则实数a的取值范围是_______.
【解析】由题意知y=ln
x(x≥1)的值域为[0,+∞),
故要使f(x)的值域为R,则必有y=(1-2a)x+3a为增函数,
且1-2a+3a≥0,所以1-2a>0且a≥-1,解得-1≤a<
,
实数a的取值范围是
.
答案:
20.如果二次函数f(x)=x2-(a-1)x+5在区间(
,1)上是增函数,则实数a的取值范
围为________.?
【解析】因为函数f(x)=x2-(a-1)x+5的对称轴为直线x=
且在区间
上是增函数,
所以
≤
,即a≤2.
故实数a的取值范围为(-∞,2].
答案:(-∞,2]
21.某部影片的盈利额(即影片的票房收入与固定成本之差)记为y,观影人数记为x,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后y与x的函数图象.
给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是________.(填写所有正确说法的编号)?
【解析】由图象(1)可设盈利额y与观影人数x的函数为y=kx+b,k>0,b<0,即k为票价,当k=0时,y=b,则-b为固定成本,由图象(2)知,直线向上平移,k不变,即票价不变,b变大,则-b变小,成本减小.故①错误,②正确;由图象(3)知,直线与y轴的交点不变,直线斜率变大,k变大,即提高票价,
b不变,则-b不变,成本不变.故③正确,④错误;
答案:②③
22.如图所示为函数在区间(-1,2]上的图象,则此函数的解析式f(x)=________.?
【解析】由图象可知,每一段都是一次函数,设f(x)=kx+b,k≠0,当x∈(-1,0)时,
直线过点(-1,0),(0,1),所以
,所以f(x)=x+1,当x∈[0,2]时,直线过点
(0,0),(2,-1),所以
,解得
,所以f(x)=-
x,
所以f(x)=
答案:
23.当生物死亡后,它机体内原有的碳14会按确定的规律衰减.大约每经过5
730
年衰减为原来的一半,这个时间称为“半衰期”.当死亡生物组织内的碳14的含
量不足死亡前的千分之一时,用一般的放射性探测器就测不到碳14了.如果用一
般的放射性探测器不能测到碳14,那么死亡生物组织内的碳14至少经过了
________个“半衰期”.(提示:
≈0.001
95)?
【解析】设生物组织内原有的碳14含量为x,
需要经过n个“半衰期”才不能测到碳14,
则x·
<
x,即
<0.001,
由参考数据可知,
≈0.001
95>0.001,
≈0.001
95×
=0.000
975<0.001,所以n=10.
答案:10
24.使log2(-x)
x+1成立的x的取值范围是(-1,0).
答案:(-1,0)
25.函数y=
+
+1的值域为________.
25.【解析】令t=
,t∈(0,+∞),则原函数可化为y=t2+t+1=
,因为
函数y=
在(0,+∞)是增函数,所以y>
=1,即原函数的值域是
(1,+∞).
答案:(1,+∞)
26.已知偶函数y=f(x)(x∈R)在区间[-1,0]上单调递增,且满足f(1-x)+f(1+x)=0,给出下列判断:
①f(5)=0;
②f(x)在[1,2]上是减函数;
③函数f(x)没有最小值;
④函数f(x)在x=0处取得最大值;
⑤f(x)的图象关于直线x=1对称.
其中判断正确的序号是________.?
26.【解析】因为f(1-x)+f(1+x)=0,
所以f(1+x)=-f(1-x)=-f
,
所以f(2+x)=-f(x),所以f(x+4)=f(x),即函数f(x)是周期为4的周期函数.
由题意知,函数y=f(x)
关于点
对称,画出满足条件的图象如图所示,
结合图象可知①②④正确.
答案:①②④
27.函数f(x)的定义域为[-1,1),其图象如图所示.函数g(x)是定义域为R的奇函数,满足g(2-x)+g(x)=0,且当x∈(0,1)时,g(x)=f(x).给出下列三个结论:
①g(0)=0;②函数g(x)在(-1,5)内有且仅有3个零点;③不等式f(-x)<0的解集为{x|-1
27.【解析】因为函数y=g(x)是奇函数,所以g(x)=-g(-x),
又g(2-x)+g(x)=0,所以g(2-x)=g(-x),即g(x+2)=g(x),
所以,函数y=g(x)的周期为2.
对于①,由于函数y=g(x)是R上的奇函数,
所以,g(0)=0,故①正确;
对于②,因为g(2-x)+g(x)=0,令x=1,可得2g(1)=0,得g(1)=0,
所以,函数y=g(x)在区间(-1,1]上的零点为0和1.
因为函数y=g(x)的周期为2,
所以函数y=g(x)在(-1,5)内有5个零点,分别是0,1,2,3,4,故②错误;
对于③,令t=-x,则需求f(t)<0的解集,
由图象可知,0
28.已知函数f(x)=x3+x,若关于x的不等式f(mx2+2)
+f(-x)<0在区间[1,5]上有解,则实数m的取值范围为________.?
【解析】由f(x)=x3+x知,f′(x)=3x2+1>0
,所以f(x)在R上单调递增;因为
f(-x)=-x3-x=-f(x)
且函数定义域为R,所以f(x)
为奇函数,则f(mx2+2)+f(-x)<0
即为f(mx2+2)<-f(-x)=f(x),由函数单调递增可知,mx2+2
在区间[1,5]上有解,只需m<
,令g(x)=
,x∈[1,5],则
g′(x)=
,令g′(x)=0,解得x=4
,因为当x∈[1,4)时,g′(x)=
>0,
则g(x)在x∈[1,4)单调递增;当x∈[4,5]时,g′(x)=
<0,则g(x)在x∈[4,5]
单调递减.所以,当x=4
时,g(x)有最大值为g(4)=
,故m<
.
答案:m<
同课章节目录
