函数与方程导数的几何意义课件(共35张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 函数与方程导数的几何意义课件(共35张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 496.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 20:32:49 | ||
图片预览











文档简介
(共35张PPT)
函数与方程、导数的几何意义
真题再研析·提升审题力
考向一 函数零点的应用
【典例】已知函数
,
若g(x)存在2个零点②,则a的取值范围是( )
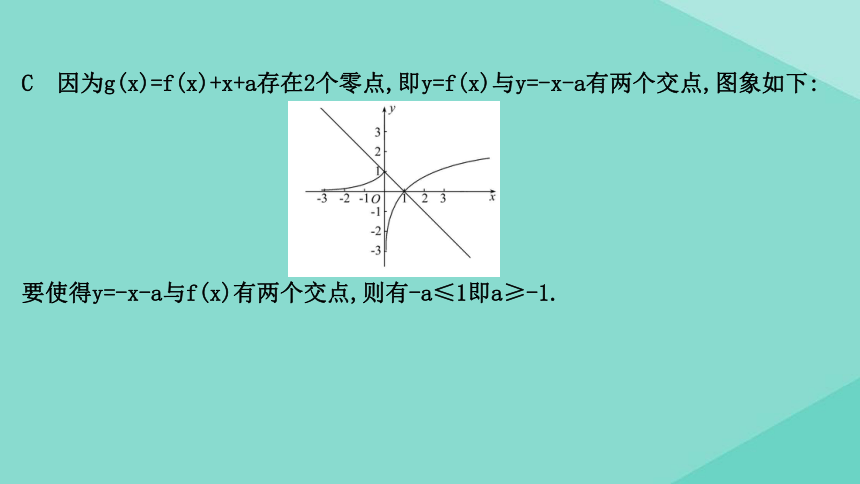
C 因为g(x)=f(x)+x+a存在2个零点,即y=f(x)与y=-x-a有两个交点,图象如下:
要使得y=-x-a与f(x)有两个交点,则有-a≤1即a≥-1.
【题眼直击】
①
分段函数,函数图象,数形结合
②
零点转化为图象交点
考向二 导数的几何意义
【典例】(2020·全国Ⅲ卷)设函数f(x)=
.若f′(1)=
,则a=________.?
【解析】由函数的解析式可得:
f′(x)=
,
则f′(1)=
,
所以
,
所以a2-2a+1=0,解得:a=1.
答案:1
【考前必备】
1.巧用曲线、切线、切点
(1)切点处的导数是切线的斜率;
(2)切点在切线上;
(3)切点在曲线上.
2.处理函数与方程必记两结论
(1)若连续不断的函数f(x)在定义域上是单调函数,则f(x)至多有一个零点.函数的零点不是一个“点”,而是方程f(x)=0的实根.
(2)由函数y=f(x)(图象是连续不断的)在闭区间[a,b]上有零点不一定能推出f(a)·f(b)<0,如图所示,所以f(a)·f(b)<0是y=f(x)在闭区间[a,b]上有零点的充分不必要条件.
【考场秘技】
1.函数中的转化思想
(1)方程f(x)-g(x)=0解的个数问题可转化为两个函数y=f(x),y=g(x)图象交点的个数问题;
(2)已知方程有解求参数范围问题可转化为函数值域问题.
2.判断函数零点个数的常用方法
(1)通过解方程来判断.
(2)根据零点存在性定理,结合函数性质来判断.
(3)将函数y=f(x)-g(x)的零点个数转化为函数y=f(x)与y=g(x)图象公共点的个数
【命题陷阱】
1.对f′(x0)与f′(x)理解有误
【案例】T1,应先求导再求函数值,同时要注意f′(1)是常数.
2.忽视切点的位置
【案例】T4求曲线的切线方程要注意分清已知点是否是切点.若已知点是切点,则可通过点斜式直接写方程,若已知点不是切点,则需设出切点.
3.忽视了“至少有一个零点”与“零点存在性定理”的不等价致错
【案例】T10,错解是因为对至少一个零点理解不透彻,至少有一个零点即有一个或多个零点,结合函数对称轴及判别式即可求解.
1.已知函数f(x)=x2+2xf′(1),则f′(0)的值为( )
A.0
B.-4
C.-2
D.2
高考演兵场·检验考试力
B 由f(x)=x2+2xf′(1),得f′(x)=2x+2f′(1).
所以f′(1)=2×1+2f′(1).
所以f′(1)=-2.从而f′(x)=2x-4.所以f′(0)=-4.
2.函数f(x)=
的零点所在的区间是
( )
A.(0,1)
B.(1,2)
C.(2,e)
D.(3,4)
B 因为f(1)=ln
2-2e2-2=0,f(2)=ln
3-1>ln
e-1=0,
则f(1)f(2)<0,所以函数f(x)=ln(x+1)-
的零点所在区间是
(1,2),
当x>0,且x→0时,f(x)=
ln(x+1)-
<0
f(e)=ln(e+1)-
>ln
e-
>0,
f(3)=ln(3+1)-
>ln
e-
>0,
f(4)=ln(4+1)-
>ln
e-
>0,
故选B.
3.函数f(x)=x+
在x=1处的切线方程为2x-y+b=0,则a+b=
( )
A.-3
B.-1
C.0
D.1
A 由题知f′(x)=1-
,则f′(1)=1-a=2,得a=-1,则切点为(1,0),又由切点
(1,0)在切线2x-y+b=0上,得b=-2,则a+b=-3.
4.已知函数f(x)=x+
.若曲线y=f(x)存在两条过(1,0)点的切线,则a的取值范围是
( )
A.(-∞,1)∪(2,+∞)
B.(-∞,-1)∪(2,+∞)
C.(-∞,0)∪(2,+∞)
D.(-∞,-2)∪(0,+∞)
D f′(x)=1-
,设切点坐标为
,
则切线方程为
,
又切线过点(1,0),可得
,
整理得2
+2ax0-a=0,曲线存在两条切线,
故方程有两个不等实根,
即满足Δ=4a2-8(-a)>0,解得a>0或a<-2.
5.我们处在一个有声世界里,不同场合,人们对声音的音量会有不同要求.音量大
小的单位是分贝(dB),对于一个强度为I的声波,其音量的大小η可由如下公式计
算:η=10lg
(其中I0是人耳能听到声音的最低声波强度),则70
dB的声音的声
波强度I1是60
dB的声音的声波强度I2的
( )
A.
倍
B.10
倍
C.10倍
D.ln
倍
C 由η=10lg
得I=I01
,
所以I1=I0107,I2=I0106,
所以
=10,
所以70
dB的声音的声波强度I1是60
dB的声音的声波强度I2的10倍.
6.若函数f(x)=
x3+x2-ax在区间(1,+∞)上单调递增,且在区间(1,2)上有零点,则实数a的取值范围是
( )
C 因为函数f(x)=
x3+x2-ax,则f′(x)=x2+2x-a,其对称轴为x=-1,
f′(x)在区间(1,+∞)上单调递增,又有函数f(x)在区间(1,+∞)上单调递增,
等价于在区间(1,+∞)上f′(x)≥0恒成立,则f′(x)min>f′(1)=3-a≥0?a≤3,
由零点的存在性定理可知,函数f(x)在区间(1,2)上有零点且单调递增,
则f(1)·f(2)<0?
<0?
,
综上,实数a的取值范围是
.
7.已知x0是函数f(x)=2x+
的一个零点,若x1∈(1,x0),x2∈(x0+∞),则
( )
A.f(x1)<0,f(x2)<0
B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0
D.f(x1)>0,f(x2)>0
B 因为x0是函数f(x)=2x+
的一个零点,则x0是函数y=2x与y=
的交点的横
坐标,画出函数图象,如图所示,则当x1∈(1,x0)时,y=2x在y=
下方,即f(x1)<0;
当x2∈(x0,+∞)时,y=2x在y=
上方,即f(x2)>0,故选B.
8.已知α,β(α<β)是方程(x-a)(x-b)+2=0的两根,其中a( )
A.a<α<βB.a<αC.αD.αA 设函数y=(x-a)(x-b)+2,图象为开口向上的抛物线,x=α,x=β是抛物线与x轴交点的横坐标,而当x=a时,函数值y=2>0,所以a在α的左边,即a<α,同理β9.定义域和值域均为[-a,a](常数a>0)的函数y=f(x)和y=g(x)的图象如图所示,方程g[f(x)]=0解的个数不可能是
( )
A.1
B.2
C.3
D.4
D 因为x∈[-a,a]时,g(x)=0有唯一解,不妨设唯一解为k,由g(x)图象可知k∈(0,a),则由g[f(x)]=0可得f(x)=k,因为k∈(0,a),由f(x)图象可知,f(x)=k可能有1根,2根,3个根,不可能有4个根,故选D.
10.若函数f(x)=x2-2ax+2在(0,4)上至少有一个零点,则实数a的取值范围为________.?
【解析】因为函数f(x)=x2-2ax+2在(0,4)上至少有一个零点,且f(0)=2>0,
所以f(4)<0或
解得a>
或
≤a<4,即a≥
.
所以实数a的取值范围为
.
答案:
11.已知函数
,则f(f(0))=________;设函数g(x)=f(x)-kx存在
3个零点,则实数k的取值范围是________.?
【解析】因为f(x)=
所以f(f(0))=f(1)=0,
因为函数g(x)=f(x)-kx存在3个零点,所以方程f(x)=kx存在3个根,
即y=kx与y=f(x)存在3个交点,
设y=kx与f(x)=e-x(x≤0)相切于点(x0,
),
则
=f′(x0)=
,解得x0=-1,
所以k=-e,如图,
由图可知,当k<-e时,y=kx与y=f(x)存在3个交点.
答案:0 (-∞,-e)
12.已知函数
若关于x的方程f(x)=kx+1有3个互异的实数解,
则实数k的取值范围是________.?
【解析】作图y=f(x)如下,A(1,2),直线y=kx+1过定点
P(0,1),所以实数k的取值范围是(kPB,0)∪(0,kPA),
因为kPA=1,又由y=kx+1与y=
(x≥1),
联立得kx+1=
?kx2+(k+1)x-3=0,
由y=kx+1与y=
(x≥1),相切得Δ=(k+1)2+12k=0,
因为x≥1,所以k=-7+4
,
因此实数k的取值范围是(-7+4
,0)∪(0,1)
答案:(-7+4
,0)∪(0,1)
函数与方程、导数的几何意义
真题再研析·提升审题力
考向一 函数零点的应用
【典例】已知函数
,
若g(x)存在2个零点②,则a的取值范围是( )
C 因为g(x)=f(x)+x+a存在2个零点,即y=f(x)与y=-x-a有两个交点,图象如下:
要使得y=-x-a与f(x)有两个交点,则有-a≤1即a≥-1.
【题眼直击】
①
分段函数,函数图象,数形结合
②
零点转化为图象交点
考向二 导数的几何意义
【典例】(2020·全国Ⅲ卷)设函数f(x)=
.若f′(1)=
,则a=________.?
【解析】由函数的解析式可得:
f′(x)=
,
则f′(1)=
,
所以
,
所以a2-2a+1=0,解得:a=1.
答案:1
【考前必备】
1.巧用曲线、切线、切点
(1)切点处的导数是切线的斜率;
(2)切点在切线上;
(3)切点在曲线上.
2.处理函数与方程必记两结论
(1)若连续不断的函数f(x)在定义域上是单调函数,则f(x)至多有一个零点.函数的零点不是一个“点”,而是方程f(x)=0的实根.
(2)由函数y=f(x)(图象是连续不断的)在闭区间[a,b]上有零点不一定能推出f(a)·f(b)<0,如图所示,所以f(a)·f(b)<0是y=f(x)在闭区间[a,b]上有零点的充分不必要条件.
【考场秘技】
1.函数中的转化思想
(1)方程f(x)-g(x)=0解的个数问题可转化为两个函数y=f(x),y=g(x)图象交点的个数问题;
(2)已知方程有解求参数范围问题可转化为函数值域问题.
2.判断函数零点个数的常用方法
(1)通过解方程来判断.
(2)根据零点存在性定理,结合函数性质来判断.
(3)将函数y=f(x)-g(x)的零点个数转化为函数y=f(x)与y=g(x)图象公共点的个数
【命题陷阱】
1.对f′(x0)与f′(x)理解有误
【案例】T1,应先求导再求函数值,同时要注意f′(1)是常数.
2.忽视切点的位置
【案例】T4求曲线的切线方程要注意分清已知点是否是切点.若已知点是切点,则可通过点斜式直接写方程,若已知点不是切点,则需设出切点.
3.忽视了“至少有一个零点”与“零点存在性定理”的不等价致错
【案例】T10,错解是因为对至少一个零点理解不透彻,至少有一个零点即有一个或多个零点,结合函数对称轴及判别式即可求解.
1.已知函数f(x)=x2+2xf′(1),则f′(0)的值为( )
A.0
B.-4
C.-2
D.2
高考演兵场·检验考试力
B 由f(x)=x2+2xf′(1),得f′(x)=2x+2f′(1).
所以f′(1)=2×1+2f′(1).
所以f′(1)=-2.从而f′(x)=2x-4.所以f′(0)=-4.
2.函数f(x)=
的零点所在的区间是
( )
A.(0,1)
B.(1,2)
C.(2,e)
D.(3,4)
B 因为f(1)=ln
2-2
3-1>ln
e-1=0,
则f(1)f(2)<0,所以函数f(x)=ln(x+1)-
的零点所在区间是
(1,2),
当x>0,且x→0时,f(x)=
ln(x+1)-
<0
f(e)=ln(e+1)-
>ln
e-
>0,
f(3)=ln(3+1)-
>ln
e-
>0,
f(4)=ln(4+1)-
>ln
e-
>0,
故选B.
3.函数f(x)=x+
在x=1处的切线方程为2x-y+b=0,则a+b=
( )
A.-3
B.-1
C.0
D.1
A 由题知f′(x)=1-
,则f′(1)=1-a=2,得a=-1,则切点为(1,0),又由切点
(1,0)在切线2x-y+b=0上,得b=-2,则a+b=-3.
4.已知函数f(x)=x+
.若曲线y=f(x)存在两条过(1,0)点的切线,则a的取值范围是
( )
A.(-∞,1)∪(2,+∞)
B.(-∞,-1)∪(2,+∞)
C.(-∞,0)∪(2,+∞)
D.(-∞,-2)∪(0,+∞)
D f′(x)=1-
,设切点坐标为
,
则切线方程为
,
又切线过点(1,0),可得
,
整理得2
+2ax0-a=0,曲线存在两条切线,
故方程有两个不等实根,
即满足Δ=4a2-8(-a)>0,解得a>0或a<-2.
5.我们处在一个有声世界里,不同场合,人们对声音的音量会有不同要求.音量大
小的单位是分贝(dB),对于一个强度为I的声波,其音量的大小η可由如下公式计
算:η=10lg
(其中I0是人耳能听到声音的最低声波强度),则70
dB的声音的声
波强度I1是60
dB的声音的声波强度I2的
( )
A.
倍
B.10
倍
C.10倍
D.ln
倍
C 由η=10lg
得I=I01
,
所以I1=I0107,I2=I0106,
所以
=10,
所以70
dB的声音的声波强度I1是60
dB的声音的声波强度I2的10倍.
6.若函数f(x)=
x3+x2-ax在区间(1,+∞)上单调递增,且在区间(1,2)上有零点,则实数a的取值范围是
( )
C 因为函数f(x)=
x3+x2-ax,则f′(x)=x2+2x-a,其对称轴为x=-1,
f′(x)在区间(1,+∞)上单调递增,又有函数f(x)在区间(1,+∞)上单调递增,
等价于在区间(1,+∞)上f′(x)≥0恒成立,则f′(x)min>f′(1)=3-a≥0?a≤3,
由零点的存在性定理可知,函数f(x)在区间(1,2)上有零点且单调递增,
则f(1)·f(2)<0?
<0?
综上,实数a的取值范围是
.
7.已知x0是函数f(x)=2x+
的一个零点,若x1∈(1,x0),x2∈(x0+∞),则
( )
A.f(x1)<0,f(x2)<0
B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0
D.f(x1)>0,f(x2)>0
B 因为x0是函数f(x)=2x+
的一个零点,则x0是函数y=2x与y=
的交点的横
坐标,画出函数图象,如图所示,则当x1∈(1,x0)时,y=2x在y=
下方,即f(x1)<0;
当x2∈(x0,+∞)时,y=2x在y=
上方,即f(x2)>0,故选B.
8.已知α,β(α<β)是方程(x-a)(x-b)+2=0的两根,其中a
A.a<α<β
( )
A.1
B.2
C.3
D.4
D 因为x∈[-a,a]时,g(x)=0有唯一解,不妨设唯一解为k,由g(x)图象可知k∈(0,a),则由g[f(x)]=0可得f(x)=k,因为k∈(0,a),由f(x)图象可知,f(x)=k可能有1根,2根,3个根,不可能有4个根,故选D.
10.若函数f(x)=x2-2ax+2在(0,4)上至少有一个零点,则实数a的取值范围为________.?
【解析】因为函数f(x)=x2-2ax+2在(0,4)上至少有一个零点,且f(0)=2>0,
所以f(4)<0或
解得a>
或
≤a<4,即a≥
.
所以实数a的取值范围为
.
答案:
11.已知函数
,则f(f(0))=________;设函数g(x)=f(x)-kx存在
3个零点,则实数k的取值范围是________.?
【解析】因为f(x)=
所以f(f(0))=f(1)=0,
因为函数g(x)=f(x)-kx存在3个零点,所以方程f(x)=kx存在3个根,
即y=kx与y=f(x)存在3个交点,
设y=kx与f(x)=e-x(x≤0)相切于点(x0,
),
则
=f′(x0)=
,解得x0=-1,
所以k=-e,如图,
由图可知,当k<-e时,y=kx与y=f(x)存在3个交点.
答案:0 (-∞,-e)
12.已知函数
若关于x的方程f(x)=kx+1有3个互异的实数解,
则实数k的取值范围是________.?
【解析】作图y=f(x)如下,A(1,2),直线y=kx+1过定点
P(0,1),所以实数k的取值范围是(kPB,0)∪(0,kPA),
因为kPA=1,又由y=kx+1与y=
(x≥1),
联立得kx+1=
?kx2+(k+1)x-3=0,
由y=kx+1与y=
(x≥1),相切得Δ=(k+1)2+12k=0,
因为x≥1,所以k=-7+4
,
因此实数k的取值范围是(-7+4
,0)∪(0,1)
答案:(-7+4
,0)∪(0,1)
同课章节目录
