集合与常用逻辑用语课件(共30张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 集合与常用逻辑用语课件(共30张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 407.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 19:19:24 | ||
图片预览










文档简介
(共30张PPT)
集合与常用逻辑用语
真题再研析·提升审题力
考向一 集合的基本运算
【典例】(2020·全国Ⅰ卷)已知集合A={x|x2-3x-4<0},B={-4,1,3,5},则A∩B=
( )
A.{-4,1}
B.{1,5}
C.{3,5}
D.{1,3}
D 由x2-3x-4<0解得-1所以A=
又因为B=
所以A∩B=
考向二 充分条件、必要条件
【典例】(2019·全国Ⅱ卷)设α,β为两个平面,则α∥β的充要条件是
( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面
B 当α内有无数条直线与β平行时,也可能两平面相交,故A错.同样当α,β平行于同一条直线或α,β垂直于同一平面时,两平面也可能相交,故C,D错.由面面平行的判定定理可得B正确.
【考前必备】
1.集合运算的四种性质
(1)A∪?=A,A∩?=?;
(2)A∪B=A?B?A?A∩B=B;
(3)A∪
=U;A∩
=?;
(4)
=
∩
;
=
∪
.
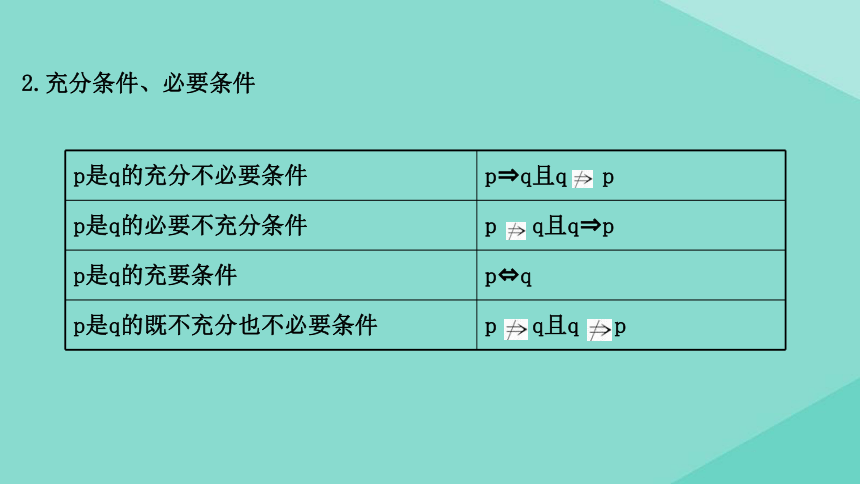
2.充分条件、必要条件
p是q的充分不必要条件
p?q且q
p
p是q的必要不充分条件
p
q且q?p
p是q的充要条件
p?q
p是q的既不充分也不必要条件
p
q且q
p
【考场秘技】
1.活用数轴与Venn图解决集合运算
(1)连续区间集合运算用数轴;
(2)列举法表示的集合用Venn图.
2.巧判断充分条件、必要条件
(1)定义法:第一步,分清条件和结论;第二步,找推式:判断p?q及q?p的真假;第
三步,下结论:根据推式及定义下结论;
(2)集合法:记条件p,q对应的集合分别为A,B,若A
B,则p是q的充分不必要条件;
若B
A,则p是q的必要不充分条件;若A=B,则p是q的充要条件.
【命题陷阱】
1.集合运算中容易忽略函数的定义域
【案例】T3要注意log2x≤3中x>0.
2.忽略相等集合
【案例】T5
A=C=B时,满足题意.
3.混淆充分不必要与必要不充分的关系
【案例】T8由条件推结论能推出,但是由结论推条件推不出,故为充分不必要条件.
4.不能理解充要条件的定义,即条件与结论可以互推
【案例】T9由条件可得ac-bd=0且ad+bc≠0,同时,只要满足ac-bd=0且ad+bc≠0,即可使条件成立,故条件与结论可以互推.
1.设集合A={x|x2-5x+6>0},B={
x|x-1<0},则A∩B=
( )
A.(-∞,1)
B.(-2,1)
C.(-3,-1)
D.(3,+∞)
高考演兵场·检验考试力
A 由题意得,
则A∩B=
.
2.设集合M={x|x2+x-6<0},N={x|1≤x≤3},则M∪N=
( )
A.[1,2)
B.[1,2]
C.(-3,3]
D.[2,3]
C 因为M={x|x2+x-6<0}=(-3,2),
所以M∪N=(-3,3].
3.设集合A={x||3x+1|≤4},B={x|log2x≤3},则A∪B=
( )
A.[0,1]
B.(0,1]
C.
D.
C 解
≤4得,-
≤x≤1,则集合A=
;解
log2x≤3得0B=
,所以A∪B=
4.若全集U={1,2,3,4,5,6},M={1,3,4},N={2,3,4},则集合
∪
等于
( )
A.{5,6}
B.{1,5,6}
C.{2,5,6}
D.{1,2,5,6}
D
={2,5,6},
={1,5,6},(
)∪(
)={1,2,5,6}.
5.已知集合A=
B=
则满足条件
A?C?B的集合C的个数为
( )
A.1
B.2
C.3
D.4
D 求解一元二次方程,得A=
易知B=
因为A?C?B,所以根据子集的定义,集合C必须含有元素1,2,且可能含有元素
3,4,原题即求集合
的子集个数,即有22=4个.
6.已知集合A={x|y=
},B={x|a≤x≤a+1},若B?A,则实数a的取值范围为
( )
A.(-∞,-3]∪[2,+∞)
B.[-1,2]
C.[-2,1]
D.[2,+∞)
C 集合A={x|y=
}={x|-2≤x≤2},因为B?A,所以有
所以-2≤a≤1.
7.已知集合A={x|a-1A.(-∞,-2)
B.(-∞,-2]
C.(-2,+∞)
D.[-2,+∞)
B 因为A∩B=A,所以A?B,
当A=?时,a-1≥2a+1,解得a≤-2;
当A≠?时,有
不等式组无解.
综上所述,实数a的取值范围是(-∞,-2].
8.“ln
x>ln
y”是“
”的
( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
A 由ln
x>ln
y,得x>y>0,此时
,反之
成立时,可以取x=-1,y=-2,不能推出ln
x>ln
y.
9.复数a+bi与c+di(a,b,c,d∈R)的积是纯虚数的充要条件是
( )
A.ac-bd=0
B.ad+bc=0
C.ac-bd≠0且ad+bc=0
D.ac-bd=0且ad+bc≠0
D (a+bi)(c+di)=(ac-bd)+(bc+ad)i是纯虚数,
则ac-bd=0且ad+bc≠0,而当ac-bd=0且ad+bc≠0时,(a+bi)(c+di)=
(ac-bd)+(bc+ad)i是纯虚数,所以,(a+bi)(c+di)=(ac-bd)+(bc+ad)i是纯虚数的一个充要条件是ac-bd=0且ad+bc≠0.
10.若a,b∈R,则“a-b>0”是“
>ab”的
( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
10.A a,b∈R,若a-b>0,则
-ab=
=
>0,即
>ab,
若
>ab,即
-ab=
=
>0,则a-b>0或a-b<0,所以若
a,b∈R,则“a-b>0”是“
>ab”的充分不必要条件.
11.在△ABC中,sin
A>cos
B是△ABC为锐角三角形的
( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
11.B 若B为钝角,A为锐角,则sin
A>0,cos
B<0,则满足sin
A>cos
B,但△ABC
为锐角三角形不成立,充分性不成立;若△ABC为锐角三角形,则A,B,π-A-B都是
锐角,即π-A-B<
,即A+B>
,
>B>
-A>0,则cos
B,即cos
BA,
必要性成立;故“sin
A>cos
B”是“△ABC为锐角三角形”的必要不充分条件.
12.命题p:?x≥0,都有ex≥-x+1,则命题p的否定为
( )
A.?x≥0,都有ex<-x+1
B.?x<0,都有ex≥-x+1
C.?x0≥0,
<-x0+1
D.?x0<0,
<-x0+1
C 因为命题p:?x≥0,都有ex≥-x+1,所以命题p的否定为?x0≥0,
<-x0+1.
13.已知p:x≤1+m,q:|x-4|≤6.若p是q的必要不充分条件,则m的取值范围是( )
A.(-∞,-1]
B.(-∞,9]
C.[1,9]
D.[9,+∞)
D 由|x-4|≤6,解得-2≤x≤10,因为p是q的必要不充分条件,所以m+1≥10,解得m≥9.
集合与常用逻辑用语
真题再研析·提升审题力
考向一 集合的基本运算
【典例】(2020·全国Ⅰ卷)已知集合A={x|x2-3x-4<0},B={-4,1,3,5},则A∩B=
( )
A.{-4,1}
B.{1,5}
C.{3,5}
D.{1,3}
D 由x2-3x-4<0解得-1
又因为B=
所以A∩B=
考向二 充分条件、必要条件
【典例】(2019·全国Ⅱ卷)设α,β为两个平面,则α∥β的充要条件是
( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面
B 当α内有无数条直线与β平行时,也可能两平面相交,故A错.同样当α,β平行于同一条直线或α,β垂直于同一平面时,两平面也可能相交,故C,D错.由面面平行的判定定理可得B正确.
【考前必备】
1.集合运算的四种性质
(1)A∪?=A,A∩?=?;
(2)A∪B=A?B?A?A∩B=B;
(3)A∪
=U;A∩
=?;
(4)
=
∩
;
=
∪
.
2.充分条件、必要条件
p是q的充分不必要条件
p?q且q
p
p是q的必要不充分条件
p
q且q?p
p是q的充要条件
p?q
p是q的既不充分也不必要条件
p
q且q
p
【考场秘技】
1.活用数轴与Venn图解决集合运算
(1)连续区间集合运算用数轴;
(2)列举法表示的集合用Venn图.
2.巧判断充分条件、必要条件
(1)定义法:第一步,分清条件和结论;第二步,找推式:判断p?q及q?p的真假;第
三步,下结论:根据推式及定义下结论;
(2)集合法:记条件p,q对应的集合分别为A,B,若A
B,则p是q的充分不必要条件;
若B
A,则p是q的必要不充分条件;若A=B,则p是q的充要条件.
【命题陷阱】
1.集合运算中容易忽略函数的定义域
【案例】T3要注意log2x≤3中x>0.
2.忽略相等集合
【案例】T5
A=C=B时,满足题意.
3.混淆充分不必要与必要不充分的关系
【案例】T8由条件推结论能推出,但是由结论推条件推不出,故为充分不必要条件.
4.不能理解充要条件的定义,即条件与结论可以互推
【案例】T9由条件可得ac-bd=0且ad+bc≠0,同时,只要满足ac-bd=0且ad+bc≠0,即可使条件成立,故条件与结论可以互推.
1.设集合A={x|x2-5x+6>0},B={
x|x-1<0},则A∩B=
( )
A.(-∞,1)
B.(-2,1)
C.(-3,-1)
D.(3,+∞)
高考演兵场·检验考试力
A 由题意得,
则A∩B=
.
2.设集合M={x|x2+x-6<0},N={x|1≤x≤3},则M∪N=
( )
A.[1,2)
B.[1,2]
C.(-3,3]
D.[2,3]
C 因为M={x|x2+x-6<0}=(-3,2),
所以M∪N=(-3,3].
3.设集合A={x||3x+1|≤4},B={x|log2x≤3},则A∪B=
( )
A.[0,1]
B.(0,1]
C.
D.
C 解
≤4得,-
≤x≤1,则集合A=
;解
log2x≤3得0
,所以A∪B=
4.若全集U={1,2,3,4,5,6},M={1,3,4},N={2,3,4},则集合
∪
等于
( )
A.{5,6}
B.{1,5,6}
C.{2,5,6}
D.{1,2,5,6}
D
={2,5,6},
={1,5,6},(
)∪(
)={1,2,5,6}.
5.已知集合A=
B=
则满足条件
A?C?B的集合C的个数为
( )
A.1
B.2
C.3
D.4
D 求解一元二次方程,得A=
易知B=
因为A?C?B,所以根据子集的定义,集合C必须含有元素1,2,且可能含有元素
3,4,原题即求集合
的子集个数,即有22=4个.
6.已知集合A={x|y=
},B={x|a≤x≤a+1},若B?A,则实数a的取值范围为
( )
A.(-∞,-3]∪[2,+∞)
B.[-1,2]
C.[-2,1]
D.[2,+∞)
C 集合A={x|y=
}={x|-2≤x≤2},因为B?A,所以有
所以-2≤a≤1.
7.已知集合A={x|a-1
B.(-∞,-2]
C.(-2,+∞)
D.[-2,+∞)
B 因为A∩B=A,所以A?B,
当A=?时,a-1≥2a+1,解得a≤-2;
当A≠?时,有
不等式组无解.
综上所述,实数a的取值范围是(-∞,-2].
8.“ln
x>ln
y”是“
”的
( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
A 由ln
x>ln
y,得x>y>0,此时
,反之
成立时,可以取x=-1,y=-2,不能推出ln
x>ln
y.
9.复数a+bi与c+di(a,b,c,d∈R)的积是纯虚数的充要条件是
( )
A.ac-bd=0
B.ad+bc=0
C.ac-bd≠0且ad+bc=0
D.ac-bd=0且ad+bc≠0
D (a+bi)(c+di)=(ac-bd)+(bc+ad)i是纯虚数,
则ac-bd=0且ad+bc≠0,而当ac-bd=0且ad+bc≠0时,(a+bi)(c+di)=
(ac-bd)+(bc+ad)i是纯虚数,所以,(a+bi)(c+di)=(ac-bd)+(bc+ad)i是纯虚数的一个充要条件是ac-bd=0且ad+bc≠0.
10.若a,b∈R,则“a-b>0”是“
>ab”的
( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
10.A a,b∈R,若a-b>0,则
-ab=
=
>0,即
>ab,
若
>ab,即
-ab=
=
>0,则a-b>0或a-b<0,所以若
a,b∈R,则“a-b>0”是“
>ab”的充分不必要条件.
11.在△ABC中,sin
A>cos
B是△ABC为锐角三角形的
( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
11.B 若B为钝角,A为锐角,则sin
A>0,cos
B<0,则满足sin
A>cos
B,但△ABC
为锐角三角形不成立,充分性不成立;若△ABC为锐角三角形,则A,B,π-A-B都是
锐角,即π-A-B<
,即A+B>
,
>B>
-A>0,则cos
B
B
必要性成立;故“sin
A>cos
B”是“△ABC为锐角三角形”的必要不充分条件.
12.命题p:?x≥0,都有ex≥-x+1,则命题p的否定为
( )
A.?x≥0,都有ex<-x+1
B.?x<0,都有ex≥-x+1
C.?x0≥0,
<-x0+1
D.?x0<0,
<-x0+1
C 因为命题p:?x≥0,都有ex≥-x+1,所以命题p的否定为?x0≥0,
<-x0+1.
13.已知p:x≤1+m,q:|x-4|≤6.若p是q的必要不充分条件,则m的取值范围是( )
A.(-∞,-1]
B.(-∞,9]
C.[1,9]
D.[9,+∞)
D 由|x-4|≤6,解得-2≤x≤10,因为p是q的必要不充分条件,所以m+1≥10,解得m≥9.
同课章节目录
