解三角形课件(共36张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 解三角形课件(共36张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 671.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 20:33:04 | ||
图片预览


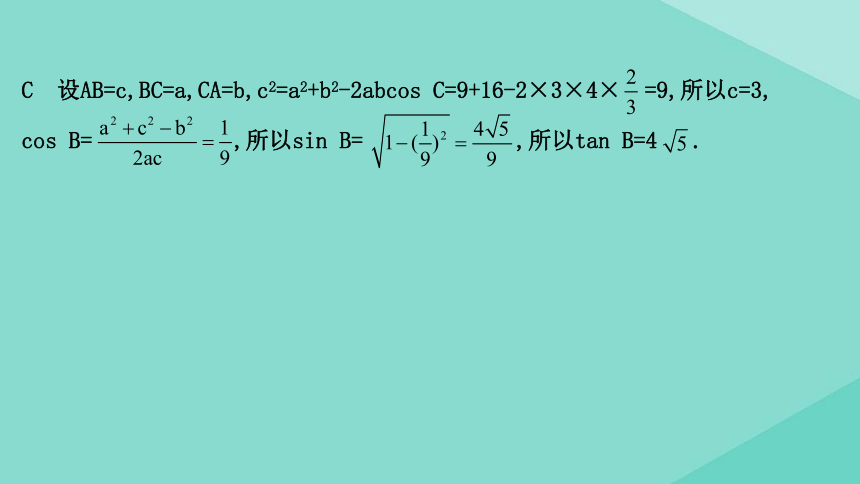








文档简介
(共36张PPT)
解
三
角
形
真题再研析·提升审题力
考向一 三角形基本量的计算
【典例】(2020·全国Ⅲ卷)在△ABC中,cos
C=
,AC=4,BC=3,则tan
B=
( )
A.
B.2
C.4
D.8
C 设AB=c,BC=a,CA=b,c2=a2+b2-2abcos
C=9+16-2×3×4×
=9,所以c=3,
cos
B=
,所以sin
B=
,所以tan
B=4
.
考向二 求三角形边角比值或求范围
【典例】(2019·全国Ⅰ卷)△ABC的内角A,B,C的对边分别为a,b,c,
已知asin
A-bsin
B=4csin
C①,cos
A=
,则
=
( )
A.6
B.5
C.4
D.3
A 由已知及正弦定理可得a2-b2=4c2,
由余弦定理推论可得-
=cos
A=
,
所以
,
所以
,
所以
,
故选A.
【题眼直击】
①
利用正弦定理转化为边的关系
②
余弦定理
【考前必备】
1.三角形中的三角函数关系
(1)sin(A+B)=sin
C;
(2)cos(A+B)=-cos
C;
(3)sin
=cos
;
(4)cos
=sin
.
2.三角形中的射影定理
在△ABC中,a=bcos
C+ccos
B;b=acos
C+ccos
A;c=bcos
A+acos
B.
3.三角形中的不等关系
(1)在△ABC中,两边之和大于第三边,两边之差小于第三边;
(2)A>B?a>b?sin
A>sin
B?cos
AB.
【考场秘技】
1.判定三角形形状的两种常用途径
2.解三角形的“口诀”
斜三角形把我问,两个定理有区分;
余弦定理多见边,正弦定理角必现;
边边角,解难辨,正弦值,先计算;
遇到边角关系时,正弦定理化边角.
【命题陷阱】
1.化简丢解
【案例】T4在判断三角形的形状时,等式两边一般不要约去公因式,应移项提取公因式,
2.未注意隐含条件导致增解
【案例】T9用余弦定理求边长时,往往会求得两个值,此时应注意题目条件中对边长的限制,对求得的值进行检验,
3.忽略已知条件
【案例】T10,审题不细,题设是锐角三角形,容易解题失误.
1.在△ABC中,角A,B,C的对边分别为a,b,c,a=2,b=3,c=4,设AB边上的高为h,
则h=
( )
高考演兵场·检验考试力
D 因为a=2,b=3,c=4,所以cos
A=
,
则sin
A=
,
则h=ACsin
A=bsin
A=3×
.
2.在△ABC中,角A,B,C的对边分别为a,b,c,c=2a,且a,b,c成等差数列,
则cos
B=
( )
A.
B.
C.
D.
D a,b,c成等差数列?2b=a+c,又c=2a,所以b=
,
cos
B=
.
3.已知锐角△ABC外接圆的半径为2,AB=2
,则△ABC周长的最大值为
( )
A.4
B.6
C.8
D.12
B 因为锐角△ABC外接圆的半径为2,AB=2
,所以
=2R,即
=4,
所以sin
C=
,又C为锐角,所以C=
,
由正弦定理得
,所以a=4sin
A,b=4sin
B,c=2
,
所以a+b+c=2
+4sin
B+4sin(
-B)=6sin
B+2
cos
B+2
=4
sin
+2
,
所以当B+
=
即B=
时,a+b+c取得最大值4
+2
=6
.
4.设△ABC的内角A,B,C所对的边分别为a,b,c,若c-acos
B=(2a-b)cos
A,则△ABC的形状为( )
A.等边三角形
B.直角三角形
C.等腰三角形或直角三角形
D.等腰直角三角形
C 因为c-acos
B=(2a-b)cos
A,C=π-(A+B),
所以由正弦定理得sin
C-sin
Acos
B=2sin
Acos
A-sin
Bcos
A,
所以sin
Acos
B+cos
Asin
B-sin
Acos
B=2sin
Acos
A-sin
Bcos
A,
所以cos
A(sin
B-sin
A)=0,所以cos
A=0或sin
B=sin
A,
所以A=
或B=A或B=π-A(舍去),
所以△ABC为等腰三角形或直角三角形.
5.设锐角三角形ABC的内角A,B,C所对的边分别为a,b,c,若a=2,B=2A,则b的取值
范围为( )
A.(0,4)
B.(2,2
)
C.(2
,2
)
D.(2
,4)
C 由锐角三角形ABC的内角A,B,C所对的边分别为a,b,c,B=2A,
得0<2A<
,A+B=3A,所
<3A<π,
所以
,所以
A<
,
因为a=2,B=2A,由正弦定理得
b=2cos
A,即b=4cos
A,
所以2
<4cos
A<2
,则b的取值范围为(2
,2
)
6.在高分辨率遥感影像上,阴影表现为低亮度值,其分布范围反映了地物成像时遮光情况的二维信息,可以通过线段AB长度(如图:粗线条部分)与建筑物高度的几何关系来确定地表建筑物的高度数据.在不考虑太阳方位角对建筑物阴影影响的情况下,太阳高度角、卫星高度角与建筑物高度、线段AB的关系如图所示,在某时刻测得太阳高度角为β,卫星高度角为α,阴影部分长度为L,由此可计算建筑物的高度为
( )
B 如图所示:由于CD⊥BD,
tan
α=
,
所以在Rt△ACD中,tan
α=
.
在Rt△BCD中,tan
β=
.
所以
,
解得x=
,所以y=
.
7.在△ABC中,已知2acos
B=c,sin
Asin
B(2-cos
C)=sin2
+
,则△ABC为
( )
A.等腰直角三角形
B.等边三角形
C.锐角非等边三角形
D.钝角三角形
A 将已知等式2acos
B=c,
利用正弦定理化简得:2sin
Acos
B=sin
C,
因为sin
C=sin(A+B)=sin
Acos
B+cos
Asin
B,
所以2sin
Acos
B=sin
Acos
B+cos
Asin
B,
即sin
Acos
B-cos
Asin
B=sin(A-B)=0,
因为A与B都为△ABC的内角,所以A-B=0,即A=B,
已知第二个等式变形得:
sin
Asin
B(2-cos
C)=
(1-cos
C)+
=1-
cos
C,
-
[cos(A+B)-cos(A-B)](2-cos
C)=1-
cos
C,
所以-
(-cos
C-1)(2-cos
C)=1-
cos
C,
即(cos
C+1)(2-cos
C)=2-cos
C,
整理得:cos2C-2cos
C=0,即cos
C(cos
C-2)=0,
所以cos
C=0或cos
C=2(舍去),所以C=90°,
则△ABC为等腰直角三角形.
8.已知在△ABC中,角A,B,C的对边分别为a,b,c,A=
,b=2,△ABC的面积等于
2
,则△ABC外接圆的面积为________.?
【解析】由
×2c·sin
=2
,解得c=4.
所以a2=22+42-2×2×4cos
=12.解得a=2
.
所以2R=
=4,解得R=2.所以△ABC外接圆的面积为4π.
答案:4π
9.△ABC的内角A,B,C的对边分别为a,b,c,若a=2,c=2
,cos
A=
,且b则b=
______.?
【解析】在△ABC中,由余弦定理得4=b2+12-2×2
b×
,
所以b2-6b+8=0,所以b=2或b=4,
因为b答案:2
10.已知△ABC是锐角三角形,若A=2B,则
的取值范围是________.?
【解析】因为A=2B,所以由正弦定理可得:
=2cos
B,因为当C
为最大角时,C<
,A+B=3B>
,B>
,当A为最大角时,A<
,2B<
,B<
,
所以
,可得:
B<
,故
∈(
,
).
答案:(
,
)
11.如图,四边形ABCD中,AB=4,BC=5,CD=3,∠ABC=90°,∠BCD=120°,则AD的长为______.?
【解析】连接AC,设∠ACB=θ,则∠ACD=120°-θ,
如图:
故在Rt△ABC中,sin
θ=
,cos
θ=
,
因为cos
=-
cos
θ+
sin
θ=-
×
+
×
=
,
又因为在△ACD中,由余弦定理有
,
解得AD2=65-12
,即AD=
答案:
12.在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=3,sin
B=sin
2A.
①
的值为________;?
②若a>c,则b的取值范围是________.?
【解析】①由sin
B=sin2A,得:sin
B=2sin
Acos
A,
由正弦定理得:b=2acos
A,即
=2a=6.
②由余弦定理,得:a2=b2+c2-2bccosA
由①得:cos
A=
所以,32=b2+c2-
,
所以,27=(3-c)b2+3c2,即:b2=
=9+3c,
因为a>c,所以,0.
答案:①6 ②(3,3
)
解
三
角
形
真题再研析·提升审题力
考向一 三角形基本量的计算
【典例】(2020·全国Ⅲ卷)在△ABC中,cos
C=
,AC=4,BC=3,则tan
B=
( )
A.
B.2
C.4
D.8
C 设AB=c,BC=a,CA=b,c2=a2+b2-2abcos
C=9+16-2×3×4×
=9,所以c=3,
cos
B=
,所以sin
B=
,所以tan
B=4
.
考向二 求三角形边角比值或求范围
【典例】(2019·全国Ⅰ卷)△ABC的内角A,B,C的对边分别为a,b,c,
已知asin
A-bsin
B=4csin
C①,cos
A=
,则
=
( )
A.6
B.5
C.4
D.3
A 由已知及正弦定理可得a2-b2=4c2,
由余弦定理推论可得-
=cos
A=
,
所以
,
所以
,
所以
,
故选A.
【题眼直击】
①
利用正弦定理转化为边的关系
②
余弦定理
【考前必备】
1.三角形中的三角函数关系
(1)sin(A+B)=sin
C;
(2)cos(A+B)=-cos
C;
(3)sin
=cos
;
(4)cos
=sin
.
2.三角形中的射影定理
在△ABC中,a=bcos
C+ccos
B;b=acos
C+ccos
A;c=bcos
A+acos
B.
3.三角形中的不等关系
(1)在△ABC中,两边之和大于第三边,两边之差小于第三边;
(2)A>B?a>b?sin
A>sin
B?cos
A
【考场秘技】
1.判定三角形形状的两种常用途径
2.解三角形的“口诀”
斜三角形把我问,两个定理有区分;
余弦定理多见边,正弦定理角必现;
边边角,解难辨,正弦值,先计算;
遇到边角关系时,正弦定理化边角.
【命题陷阱】
1.化简丢解
【案例】T4在判断三角形的形状时,等式两边一般不要约去公因式,应移项提取公因式,
2.未注意隐含条件导致增解
【案例】T9用余弦定理求边长时,往往会求得两个值,此时应注意题目条件中对边长的限制,对求得的值进行检验,
3.忽略已知条件
【案例】T10,审题不细,题设是锐角三角形,容易解题失误.
1.在△ABC中,角A,B,C的对边分别为a,b,c,a=2,b=3,c=4,设AB边上的高为h,
则h=
( )
高考演兵场·检验考试力
D 因为a=2,b=3,c=4,所以cos
A=
,
则sin
A=
,
则h=ACsin
A=bsin
A=3×
.
2.在△ABC中,角A,B,C的对边分别为a,b,c,c=2a,且a,b,c成等差数列,
则cos
B=
( )
A.
B.
C.
D.
D a,b,c成等差数列?2b=a+c,又c=2a,所以b=
,
cos
B=
.
3.已知锐角△ABC外接圆的半径为2,AB=2
,则△ABC周长的最大值为
( )
A.4
B.6
C.8
D.12
B 因为锐角△ABC外接圆的半径为2,AB=2
,所以
=2R,即
=4,
所以sin
C=
,又C为锐角,所以C=
,
由正弦定理得
,所以a=4sin
A,b=4sin
B,c=2
,
所以a+b+c=2
+4sin
B+4sin(
-B)=6sin
B+2
cos
B+2
=4
sin
+2
,
所以当B+
=
即B=
时,a+b+c取得最大值4
+2
=6
.
4.设△ABC的内角A,B,C所对的边分别为a,b,c,若c-acos
B=(2a-b)cos
A,则△ABC的形状为( )
A.等边三角形
B.直角三角形
C.等腰三角形或直角三角形
D.等腰直角三角形
C 因为c-acos
B=(2a-b)cos
A,C=π-(A+B),
所以由正弦定理得sin
C-sin
Acos
B=2sin
Acos
A-sin
Bcos
A,
所以sin
Acos
B+cos
Asin
B-sin
Acos
B=2sin
Acos
A-sin
Bcos
A,
所以cos
A(sin
B-sin
A)=0,所以cos
A=0或sin
B=sin
A,
所以A=
或B=A或B=π-A(舍去),
所以△ABC为等腰三角形或直角三角形.
5.设锐角三角形ABC的内角A,B,C所对的边分别为a,b,c,若a=2,B=2A,则b的取值
范围为( )
A.(0,4)
B.(2,2
)
C.(2
,2
)
D.(2
,4)
C 由锐角三角形ABC的内角A,B,C所对的边分别为a,b,c,B=2A,
得0<2A<
,A+B=3A,所
<3A<π,
所以
,
因为a=2,B=2A,由正弦定理得
b=2cos
A,即b=4cos
A,
所以2
<4cos
A<2
,则b的取值范围为(2
,2
)
6.在高分辨率遥感影像上,阴影表现为低亮度值,其分布范围反映了地物成像时遮光情况的二维信息,可以通过线段AB长度(如图:粗线条部分)与建筑物高度的几何关系来确定地表建筑物的高度数据.在不考虑太阳方位角对建筑物阴影影响的情况下,太阳高度角、卫星高度角与建筑物高度、线段AB的关系如图所示,在某时刻测得太阳高度角为β,卫星高度角为α,阴影部分长度为L,由此可计算建筑物的高度为
( )
B 如图所示:由于CD⊥BD,
tan
α=
,
所以在Rt△ACD中,tan
α=
.
在Rt△BCD中,tan
β=
.
所以
,
解得x=
,所以y=
.
7.在△ABC中,已知2acos
B=c,sin
Asin
B(2-cos
C)=sin2
+
,则△ABC为
( )
A.等腰直角三角形
B.等边三角形
C.锐角非等边三角形
D.钝角三角形
A 将已知等式2acos
B=c,
利用正弦定理化简得:2sin
Acos
B=sin
C,
因为sin
C=sin(A+B)=sin
Acos
B+cos
Asin
B,
所以2sin
Acos
B=sin
Acos
B+cos
Asin
B,
即sin
Acos
B-cos
Asin
B=sin(A-B)=0,
因为A与B都为△ABC的内角,所以A-B=0,即A=B,
已知第二个等式变形得:
sin
Asin
B(2-cos
C)=
(1-cos
C)+
=1-
cos
C,
-
[cos(A+B)-cos(A-B)](2-cos
C)=1-
cos
C,
所以-
(-cos
C-1)(2-cos
C)=1-
cos
C,
即(cos
C+1)(2-cos
C)=2-cos
C,
整理得:cos2C-2cos
C=0,即cos
C(cos
C-2)=0,
所以cos
C=0或cos
C=2(舍去),所以C=90°,
则△ABC为等腰直角三角形.
8.已知在△ABC中,角A,B,C的对边分别为a,b,c,A=
,b=2,△ABC的面积等于
2
,则△ABC外接圆的面积为________.?
【解析】由
×2c·sin
=2
,解得c=4.
所以a2=22+42-2×2×4cos
=12.解得a=2
.
所以2R=
=4,解得R=2.所以△ABC外接圆的面积为4π.
答案:4π
9.△ABC的内角A,B,C的对边分别为a,b,c,若a=2,c=2
,cos
A=
,且b
______.?
【解析】在△ABC中,由余弦定理得4=b2+12-2×2
b×
,
所以b2-6b+8=0,所以b=2或b=4,
因为b
10.已知△ABC是锐角三角形,若A=2B,则
的取值范围是________.?
【解析】因为A=2B,所以由正弦定理可得:
=2cos
B,因为当C
为最大角时,C<
,A+B=3B>
,B>
,当A为最大角时,A<
,2B<
,B<
,
所以
,故
∈(
,
).
答案:(
,
)
11.如图,四边形ABCD中,AB=4,BC=5,CD=3,∠ABC=90°,∠BCD=120°,则AD的长为______.?
【解析】连接AC,设∠ACB=θ,则∠ACD=120°-θ,
如图:
故在Rt△ABC中,sin
θ=
,cos
θ=
,
因为cos
=-
cos
θ+
sin
θ=-
×
+
×
=
,
又因为在△ACD中,由余弦定理有
,
解得AD2=65-12
,即AD=
答案:
12.在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=3,sin
B=sin
2A.
①
的值为________;?
②若a>c,则b的取值范围是________.?
【解析】①由sin
B=sin2A,得:sin
B=2sin
Acos
A,
由正弦定理得:b=2acos
A,即
=2a=6.
②由余弦定理,得:a2=b2+c2-2bccosA
由①得:cos
A=
所以,32=b2+c2-
,
所以,27=(3-c)b2+3c2,即:b2=
=9+3c,
因为a>c,所以,0
答案:①6 ②(3,3
)
同课章节目录
