三角函数的图象与性质课件2021高考数学二轮(共PPT98张)
文档属性
| 名称 | 三角函数的图象与性质课件2021高考数学二轮(共PPT98张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 22:15:15 | ||
图片预览


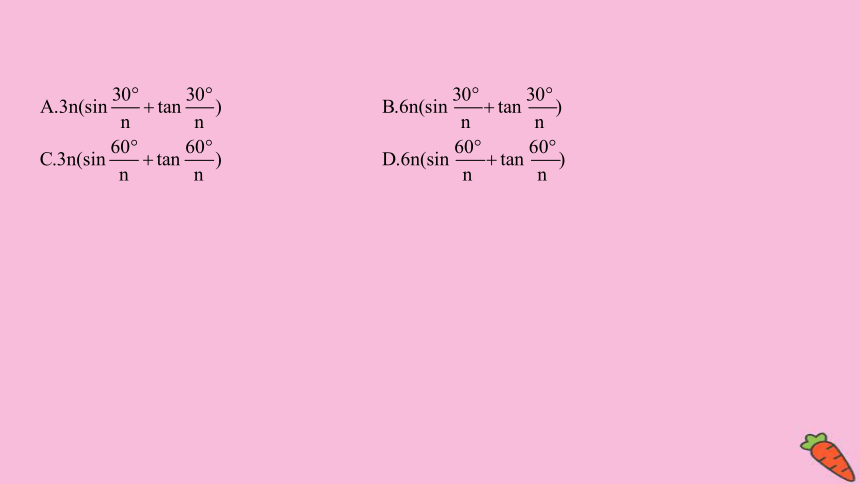







文档简介
(共98张PPT)
三角函数的图象与性质
关键能力·应用实践
考向一 三角函数的定义、诱导公式及同角三角函数基本关系
【多维题组】速通关
1.(2020·北京高考)2020年3月14日是全球首个国际圆周率日(πDay).历史上,求圆周率π的方法有多种,与中国传统数学中的“割圆术”相似,数学家阿尔·卡西的方法是:当正整数n充分大时,计算单位圆的内接正6n边形的周长和外切正6n边形(各边均与圆相切的正6n边形)的周长,将它们的算术平均数作为2π的近似值,按照阿尔·卡西的方法,π的近似值的表达式是( )
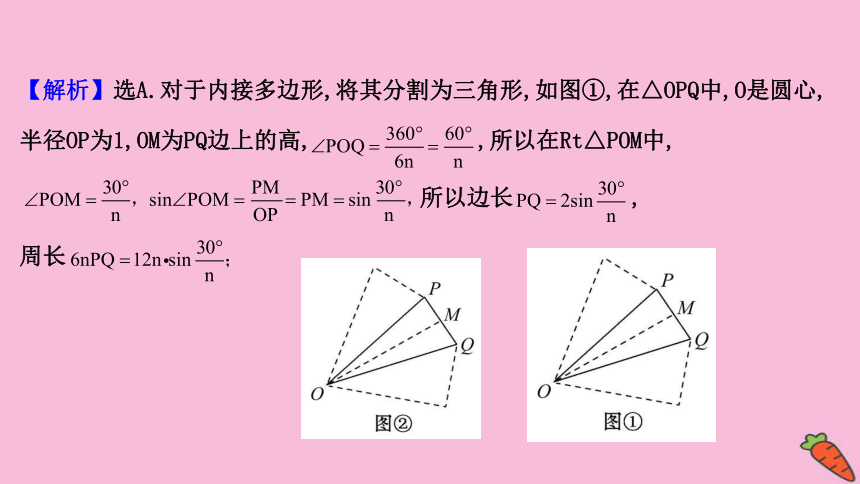
【解析】选A.对于内接多边形,将其分割为三角形,如图①,在△OPQ中,O是圆心,
半径OP为1,OM为PQ边上的高,
,所以在Rt△POM中,
所以边长
,
周长
对于外切多边形,将其分割为三角形,如图②,在△OPQ中O是圆心,半径OM为1,OM
为PQ边上的高,
,所以在Rt△POM中,
所以边长
,周长为6nPQ=12n·tan
.
综上,2π的近似值为
(12n·sin
+12n·tan
)=6n(sin
+tan
),π的
近似值为3n(sin
+tan
).
2.若tan
α=
,则sin4α+cos4α的值为________.?
【解析】因为tan
α=
,所以
所以sin4α+cos4α=(sin2α+cos2α)2-2sin2αcos2α
=1-2×
=
.
答案:
3.已知函数f(x)=ax-2+2(a>0且a≠1)过定点P,且角α的始边与x轴的正半轴重合,
终边过点P,则
=______.?
【解析】函数f(x)=ax-2+2(a>0且a≠1)过定点P(2,3),
则tan
α=
.
答案:
【变式拓展】
本题函数改为f(x)=loga(x+4)+2(a>0且a≠1),其他条件不变,则sin
sin(3π+α)=________.?
【解析】函数f(x)=loga(x+4)+2(a>0且a≠1)的图象恒过点P(-3,2),则
sin
α=
,cos
α=-
,
所以sin
sin(3π+α)
=sin
sin(π+α)=-cos
αsin
α=
.
答案:
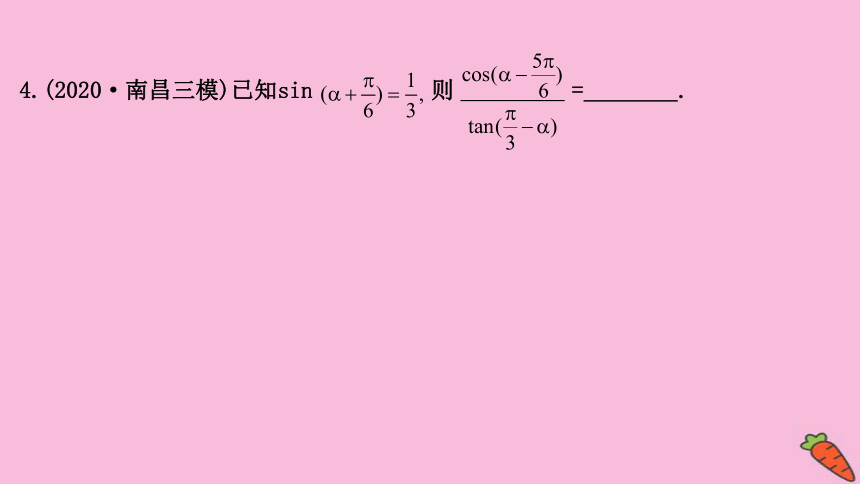
4.(2020·南昌三模)已知sin
则
=________.?
【解析】因为
所以
答案:
【技法点拨】提素养
1.三角函数:设α是一个任意角,它的终边与单位圆交于点P(x,y),则
sin
α=y,cos
α=x,tan
α=
(x≠0).各象限角的三角函数值的符号:一全正,
二正弦,三正切,四余弦.
2.利用诱导公式进行化简求值的步骤
利用诱导公式化任意角的三角函数为锐角三角函数,其步骤:去负—脱周—化锐.
特别注意函数名称和符号的确定.
提醒:“奇变偶不变,符号看象限”.
考向二 三角函数的图象
【多维题组】速通关
1.要想得到函数y=sin
2x+1的图象,只需将函数y=cos
2x的图象( )
A.向左平移
个单位长度,再向上平移1个单位长度
B.向右平移
个单位长度,再向上平移1个单位长度
C.向左平移
个单位长度,再向下平移1个单位长度
D.向右平移
个单位长度,再向下平移1个单位长度
【解析】选B.先将函数y=cos
2x=sin
的图象向右平移
个单位长度,得
到y=sin
2x的图象,再向上平移1个单位长度,即得y=sin
2x+1的图象.
【变式拓展】
本题“y=sin
2x+1”改为“y=cos
”,“y=cos
2x”改为“y=sin
2x”,
如何进行图象变换.
【解析】因为y=cos
=sin
=sin
2
所以将函数y=sin
2x的图象向左平移
个单位长度可得到函数y=cos
的图象.
2.已知函数y=
sin
2x的图象与函数y=3cos
2x的图象相邻的三个交点分别是
A,B,C,则△ABC的面积为( )
A.
B.
C.
D.
【解析】选B.函数y=
sin
2x的图象与函数y=3cos
2x的图象的交点为(x,y),
令
sin
2x=3cos
2x,故tan
2x=
,
解得2x=
+kπ(k∈Z),不妨令2x=
,
,
,
所以x=
,
,
,
即
所以三角形的底边长为π,高为
=3.
S△ABC=
×π×3=
π.
3.(2020·浙江高考)函数y=xcos
x+sin
x在区间[-π,π]的图象大致为( )
【解析】选A.-xcos
(-x)+sin
(-x)=-xcos
x-sin
x,故y=xcos
x+sin
x为奇函数,排除C,D选项,当x=π时,y=-π,故选A.
4.(2020·新高考全国Ⅰ卷)如图是函数y=sin(ωx+φ)的部分图象,则
sin(ωx+φ)=( )
【解析】选BC.令f(x)=y=sin(ωx+φ),由图象得
,所以
解得|ω|=2,故A项错误;将
代入f(x)=sin(2x+φ),得2×
+φ=kπ(k∈Z),
得φ=-
+kπ(k∈Z),令k=1,则φ=
所以f(x)=sin
即
,故C正确;由sin
α=sin(π-α),得f(x)=
sin
,故B正确;由f(0)>0,排除D.故选B,C.
【技法点拨】提素养
1.关于三角函数的图象变换的方法
(1)平移变换
①沿x轴平移:由y=f(x)变为y=f(x+φ)时,“左加右减”,即φ>0,左移;φ<0,右移.
②沿y轴平移:由y=f(x)变为y=f(x)+k时,“上加下减”,即k>0,上移;k<0,下移.
(2)伸缩变换
①沿x轴伸缩:由y=f(x)变为y=f(ωx)时,点的纵坐标不变,横坐标变为原来的
倍.
②沿y轴伸缩:由y=f(x)变为y=Af(x)时,点的横坐标不变,纵坐标变为原来的|A|
倍.
2.根据图象求解析式y=Asin
(ωx+φ)+k(A>0,ω>0)的方法
(1)在一个周期内(或者从最高点到相邻的最低点,即半个周期内),若最大值为M,
最小值为m,则A=
,k=
.特别地,当k=0时,A=M=-m.
(2)φ的求法通常有以下两种:
①代入法:把图象上的一个已知点代入(此时,A,ω,k已知),或代入图象与直线
y=k的交点求解(此时要注意交点在上升区间还是下降区间).
②五点法:确定φ值时,往往以寻找“五点法”中的零点
作为突破口,具
体如下:
“第一点”(即图象上升时与y=k的交点中距原点最近的交点)为ωx+φ=0;“第
二点”(即图象的“峰点”)为ωx+φ=
;“第三点”(即图象下降时与y=k的交
点)为ωx+φ=π;“第四点”(即图象的“谷点”)为ωx+φ=
;“第五点”为
ωx+φ=2π.
考向三 三角函数的性质(重难突破)
【多维题组】速通关
1.(2020·天津高考)已知函数f(x)=sin
.给出下列结论:
①f(x)的最小正周期为2π;
②
是f(x)的最大值;
③把函数y=sin
x的图象上所有点向左平移
个单位长度,可得到函数y=f(x)的
图象.
其中所有正确结论的序号是( )
A.①
B.①③
C.②③
D.①②③
【解析】选B.因为f(x)=sin
,所以最小正周期T=
=2π,故①正确;
故②不正确;将函数y=sin
x的图象上所有点向左平
移
个单位长度,
得到y=sin
的图象,故③正确.
2.将函数f(x)=cos
x的图象向右平移
π个单位长度,再将各点的横坐标变为原
来的
(ω>0),得到函数g(x)的图象,若g(x)在
上的值域为
则ω的范
围为( )
A.
B.
C.
D.
【考场思维】
解题方法
数形结合
整体代换
y=Acos(ωx+φ),令t=ωx+φ转化为y=Acos
t,根据条件结合图象列不等式
素养考查
数学运算、逻辑推理
【解析】选A.将函数f(x)=cos
x的图象向右平移
π个单位长度,可得
y=cos
的图象;
再将各点的横坐标变为原来的
(ω>0),
得到函数g(x)=cos
的图象.
若g(x)在
上的值域为
此时,
令t=ωx-
,则问题转化为y=cos
t,
在
上的值域为
结合图象可知,0≤
≤
,求得
≤ω≤
.
【加练备选】
已知函数f(x)=cos
,把y=f(x)的图象向左平移
个单位长度得到函数g(x)
的图象,则下列说法正确的是( )
A.
B.g(x)的图象关于直线
对称
C.g(x)的一个零点为
D.g(x)的一个单调减区间为
【考场思维】
解题方法
整体代换
结论应用
图象变换强调对自变量x本身的变换,
余弦型函数的对称轴和对称中心,
复合函数单调性遵循“同增异减”
素养考查
数学运算、逻辑推理
【解析】选D.因为f(x)=cos
=cos
所以
所以
,故A错,
令
=kπ,k∈Z,
得对称轴方程为
,k∈Z,故B错,
令
,k∈Z,
得对称中心的横坐标为
,k∈Z,故C错,
因为x∈
,故μ=2x+
∈[0,π],
因为y=cos
μ在[0,π]上是减函数,故g(x)=
上是减函数,故D正确.
3.(2020·全国Ⅲ卷)关于函数f(x)=sin
x+
有如下四个命题:
①f(x)的图象关于y轴对称.
②f(x)的图象关于原点对称.
③f(x)的图象关于直线x=
对称.
④f(x)的最小值为2.
其中所有真命题的序号是________.?
【考场思维】
【解析】对于①,由sin
x≠0可得函数的定义域为
故定义域关于
原点对称,
由f(-x)=sin(-x)+
=-sin
x-
=-f(x),
所以函数为奇函数,图象关于原点对称,
①错②对.
对于③,由于f(π-x)=sin(π-x)+
=sin
x+
=f(x),所以f(x)关于x=
对称,③对.
对于④,令t=sin
x,t∈[-1,0)∪(0,1],由对勾函数g(t)=t+
的性质,可知
g(t)∈(-∞,-2]∪[2,+∞),所以f(x)无最小值,④错.
答案:②③
【技法点拨】提素养
1.求函数单调区间的方法
(1)代换法:求形如y=Asin(ωx+φ)(或y=Acos(ωx+φ))(A,ω,φ为常数,A≠0,ω>0)的单调区间时,令ωx+φ=z,得y=Asin
z(或y=Acos
z),然后由复合函数的单调性求得.
(2)图象法:画出三角函数的图象,结合图象求其单调区间.
2.判断对称中心与对称轴的方法
利用函数y=Asin(ωx+φ)的对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点这一性质,通过检验f(x0)的值进行判断.
【变式训练】
1.(2019·全国Ⅱ卷)下列函数中,以
为周期且在区间
单调递增的是( )
A.f(x)=|cos
2x|
B.f(x)=|sin
2x|
C.f(x)=cos
|x|
D.f(x)=sin
|x|
【解析】选A.作出函数f(x)=|cos
2x|的图象,如图.
由图象可知f(x)=|cos
2x|的周期为
,在区间
上单调递增.同理可得
f(x)=|sin
2x|的周期为
,在区间
上单调递减,f(x)=cos
|x|的周期为
2π.f(x)=sin
|x|不是周期函数,排除B,C,D.
2.(多选题)函数f(x)=Acos(ωx+φ)(ω>0)的部分图象如图所示,则以下结论,正
确的有( )
A.f(x)的最小正周期为2
B.f(x)图象的一条对称轴为直线x=-
C.f(x)在(2k-
,2k+
),k∈Z上是减函数
D.f(x)的最大值为A
【解析】选AC.由题图可知,函数f(x)的最小正周期
,故A正确;因
为函数f(x)的图象过点
,所以函数f(x)图象的对称轴为直线
(k∈Z),
故直线x=-
不是函数f(x)图象的对称轴,故B错误;由题图可知,当
(k∈Z),即
(k∈Z)时,f(x)是减函数,故C正
确;若A>0,则最大值是A,若A<0,则最大值是-A,故D错误.
3.(2020·包头一模)若函数f(x)=sin
2x+cos
2x在
和[3m,π]上均单调递
增,则实数m的取值范围为________.?
【解析】f(x)=
sin
解-
+2kπ≤2x+
≤
+2kπ,k∈Z得,
-
+kπ≤x≤
+kπ,k∈Z,
当k=0时,-
≤x≤
;当k=1时,
≤x≤
,
所以f(x)在
上单调递增,
又f(x)在
,[3m,π]上单调递增,
所以
解得
≤m≤
,
所以m的取值范围为
答案:
【加练备选】
(2020·南宁二模)已知函数f(x)=sin(ωx+φ)(ω≠0)的图象经过点
,一
条对称轴方程为x=
.则函数f(x)的周期可以是( )
A.
B.
C.
D.
【解析】选B.由
T,k∈Z,
则T=
,k∈Z,当k=0时,T=
.
题组训练·素养提升
【新题速递】
1.直线l:2x-y+e=0的倾斜角为α,则sin(π-α)sin
的值为( )
A.-
B.-
C.
D.
【解析】选D.因为直线l:2x-y+e=0的倾斜角为α,
所以tan
α=2,所以sin(π-α)sin
=sin
αcos
α
2.函数f(x)=2sin
+1的图象向右平移
个单位长度后得到y=g(x)的图象,
则函数g(x)( )
A.有最大值为2
B.有最小正周期为π
C.图象关于直线x=
对称
D.为奇函数
【解析】选C.由函数f(x)=2sin
+1的图象向右平移
个单位长度后得到
y=g(x)的图象,可得g(x)=f
=2sin
+1
=2sin
+1;
可得g(x)的最大值为3,故A错误;
g(x)的最小正周期T=
,故B错误;
当x=
时g(x)=
+1=3为最大值,故C对.g(-x)=2sin
+1≠-g(x),不是奇函数,故D错误.
3.(2020·全国Ⅰ卷)设函数f(x)=cos
在[-π,π]的图象大致如图,
f(x)的最小正周期为( )
【解析】选C.由题图可得,函数图象过点
,
将它代入函数f(x)可得,cos
=0,
又
是函数f(x)图象与x轴负半轴的第一个交点,
所以
所以函数f(x)的最小正周期
4.关于函数f(x)=|cos
x|+|sin
x|有下述四个结论:
①f(x)是偶函数;②f(x)在区间
上是增函数;
③f(x)的最大值为2;④f(x)的周期为
.其中所有正确结论的编号是( )
A.①②
B.①④
C.①③④
D.②③④
【解析】选B.因为f(x)=|cos
x|+|sin
x|=
①f(-x)=|cos(-x)|+|sin(-x)|=|cos
x|+|sin
x|=f(x),
所以f(x)是偶函数,所以①正确;
②f(x)的图象如图,
由图象可知f(x)在
上不单调,②错误;
③f(x)的最大值达不到2,③错误;
④因为f
=|cos
|+|sin
|
=|sin
x|+|cos
x|=f(x),
所以函数f(x)的周期为
,
所以④正确.
【创新迁移】
1.音乐,是用声音来展现美,给人以听觉上的享受.著名数学家傅立叶研究了乐声的本质,他证明了所有的乐声都能用数学表达式来描述,它们是一些形如asin
bx的简单正弦函数的和,其中频率最低的一项是基本音,其余的为泛音.由乐声的数学表达式可知,所有泛音的频率都是基本音频率的整数倍,称为基本音的谐波.下列函数中不能与函数y=0.06sin
(180
000t)构成乐声的是( )
A.y=0.02sin
(360
000t)
B.y=0.03sin
(180
000t)
C.y=0.02sin
(181
800t)
D.y=0.05sin
(540
000t)
【解析】选C.由f=
,可知若f1=nf2(n∈N
),则必有ω1=nω2(n∈N
),故选C.
2.对任意闭区间I,用MI表示函数y=cos
x在I上的最大值,若正数a满足
M[0,a]=2M[a,2a],则a的值为( )
A.
B.
C.
D.
【解析】选D.(1)当a∈
时,2a∈[0,π],
M[0,a]=1,M[a,2a]=cos
a,
由M[0,a]=2M[a,2a],得2cos
a=1,此时a=
;
(2)当a∈
时,2a∈(π,2π),M[0,a]=1,
①当a∈
时,(2a-π)-(π-a)
=3a-2π<0,M[a,2a]=cos
a,
由M[0,a]=2M[a,2a]得cos
a=
,
在a∈
上无解;
②当a∈
时,(2a-π)-(π-a)=3a-2π≥0,
M[a,2a]=cos
2a,
由M[0,a]=2M[a,2a],得2cos
2a=1,此时a=
π;
(3)当a∈
时,2a∈[2π,3π],M[0,a]=1,
M[a,2a]=1,不合题意;
(4)当a∈
时,2a∈[3π,+∞),M[0,a]=1,
M[a,2a]=1,不合题意.综上,a的值为
或
π.
专题能力提升练
一、单项选择题(共7小题,每小题5分,共35分)
1.(2020·漳州一模)若角θ的终边经过点
,则sin
+cos(π-θ)
+tan(2π-θ)=( )
A.
B.-
C.
D.-
四 三角函数的图象与性质(35分钟 70分)
【解析】选A.由题意知tan
θ=-
,
所以sin
+cos(π-θ)+tan(2π-θ)
=cos
θ-cos
θ-tan
θ=-tan
θ=
.
2.若sin
x=3sin
,则cos
xcos
=( )
A.
B.-
C.
D.-
【解析】选A.因为sin
x=3sin
,
所以sin
x=-3cos
x,所以tan
x=-3,
所以cos
xcos
=-sin
xcos
x
3.在平面直角坐标系中,
是圆x2+y2=1上的四段弧(如图),点P在其中
一段上,角α以Ox为始边,OP为终边.若tan
ααα,则P所在的圆弧是
( )
A.
B.
C.
D.
【解析】选C.若P在
上,则由角α的三角函数线知,cos
α>sin
α,排除A;
若P在
上,则tan
α>sin
α,排除B;若P在
上,则tan
α>0,cos
α<0,
sin
α<0,排除D.
4.(2020·广州一模)设函数f(x)=2cos
,若对于任意的x∈R都有
f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为( )
A.
B.π
C.2π
D.4π
【解析】选C.函数f(x)=2cos
,若对于任意的x∈R,都有
f(x1)≤f(x)≤f(x2),
则f(x1)是函数的最小值,f(x2)是函数的最大值,|x1-x2|的最小值就是函数的
半个最小正周期
5.(2019·北京高考)设函数f(x)=cos
x+bsin
x(b为常数),则“b=0”是“f(x)为偶函数”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【解析】选C.因为f(x)=cos
x+bsin
x为偶函数,所以对任意的x∈R,都有
f(-x)=f(x),
即cos(-x)+bsin(-x)=cos
x+bsin
x,
所以2bsin
x=0.由x的任意性,得b=0.
故f(x)为偶函数?b=0.必要性成立.
反过来,若b=0,则f(x)=cos
x是偶函数.充分性成立.
所以“b=0”是“f(x)为偶函数”的充要条件.
6.(2018·全国卷Ⅱ)若f(x)=cos
x-sin
x在[-a,a]是减函数,则a的最大值是
( )
【解析】选A.f(x)=cos
x-sin
x=
cos
,且函数y=cos
x在区间[0,π]
上单调递减,则由
得
因为f(x)在[-a,a]上是减函数,
所以
解得a≤
,
所以0,所以a的最大值是
.
7.(2020·岳阳二模)已知函数f(x)=4sin
,x∈
,若函数F(x)=f(x)-3
的所有零点依次记为x1,x2,x3,…,xn,且x1=( )
A.
B.21π
C.
D.42π
【解题导引】零点即为曲线和x轴的交点的横坐标,所以先求出对称轴方程,在给
定区间
上有8条对称轴,由中点坐标公式可知x1+x2=
×2,以此类推,
xn-1+xn=
×2,各式相加,就可得出答案.
【解析】选C.令2x-
=
+kπ(k∈Z),可得x=
kπ+
(k∈Z),即函数的对称轴
方程为x=
kπ+
(k∈Z),又f(x)的周期T=π,令
kπ+
=
,可得k=8,所以函
数在x∈
上有8条对称轴.根据正弦函数的性质可知,x1+x2=
×2,x2+x3=
×2,…,xn-1+xn=
×2,(最后一条对称轴为函数的最大值点,应取前一条对应的
对称轴),将以上各式相加得x1+2x2+2x3+…+2xn-1+xn=
二、多项选择题(共15分,全部选对得5分,选对但不全的得3分,有选错的得0分)
8.若角A,B,C是△ABC的三个内角,则下列等式中一定成立的是( )
A.cos(A+B)=cos
C
B.sin(A+B)=-sin
C
C.cos
=sin
D.sin
=cos
【解析】选CD.因为A+B+C=π,所以A+B=π-C,
所以
cos(A+B)=cos(π-C)=-cos
C,sin(A+B)=sin(π-C)=sin
C,
9.已知函数f(x)=
则下列结论正确的是( )
A.f(x)不是周期函数
B.f(x)是奇函数
C.f(x)的图象关于直线x=
对称
D.f(x)在x=
处取得最大值
【解析】选AC.作出函数f(x)的图象如图:
则由图象知函数f(x)不是周期函数,故A正确;不是奇函数,故B错误,
若x>0,
=cos
cos
x-sin
sin
x=
(cos
x-sin
x),
=sin
cos
x-cos
sin
x
=
(cos
x-sin
x),
此时
若x≤0,
=sin
cos
x+cos
sin
x=
(cos
x+sin
x),
=cos
cos
x+sin
sin
x
=
,
此时
综上恒有
即图象关于直线x=
对称,故C正确,
当x=
时,f(x)=f
=cos
=0不是最大值,故D错误.
10.如图,已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,
)的图象与x轴交于
点E,F,与y轴交于点C,
=2
,∠OCF=
,|OE|=2,
则下列说法正确
的有( )
A.f(x)的最小正周期为6
B.
φ=-
C.f(x)的最大值为
D.
f(x)在区间(14,17)上单调递增
【解析】选CD.由题意可得:|OF|=
|OC|,
所以
|Asin
φ|=2+
,sin(2ω+φ)=0,
因为E(2,0),F
,C(0,Asin
φ).
所以
因为|ED|=
所以
把|Asin
φ|=
代入上式可得:
ω>0.
解得
=6,所以ω=
,可得周期T=
=12.
所以sin
=0,又因为
,所以φ=-
.可知:A,B不对.
所以
|Asin(-
)|=2+6,又因为A>0,所以A=
.
所以函数f(x)=
sin
,可知C正确.
x∈(14,17)时,
x-
∈
,可得:函数f(x)在(14,17)上单调递增.
综上可得:C,D正确.
三、填空题(共4小题,每小题5分,共20分)
11.已知函数f(x)=sin
ωx(0<ω<4)的图象向左平移
个单位后,关于点
对称,则实数ω的值为________.?
【解析】f(x)=sin
ωx(0<ω<4)的图象向左平移
个单位得g(x)=sin
的图象,因为g(x)的图象关于点
对称,
所以sin
=0,所以
=kπ,k∈Z,由0<ω<4知,当k=1时,
ω=2符合题意.
答案:2
12.已知f(x)=sin(ωx+φ)(ω>0,|φ|<π)在区间[2,4]上单调,且f(2)=1,
f(4)=-1,则ω=____________,f(x)在区间
上的值域是____________.?
【解析】由题意知f(x)的最小正周期T=4,
所以ω=
,所以f(x)=sin
又f(2)=sin(π+φ)=1,
所以π+φ=
+2kπ,k∈Z.
又|φ|<π,所以φ=-
,
所以f(x)=sin
由x∈
所以sin
即f(x)在区间
上的值域为
.
答案:
13.设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)与直线y=3的交点的横坐标构
成以π为公差的等差数列,且x=
是f(x)图象的一条对称轴,则φ=______,函数
f(x)的单调递增区间为________.?
【解析】由题意,得A=3,T=π,
所以ω=2,所以f(x)=3sin(2x+φ).
又f
=3或f
=-3,
所以2×
+φ=kπ+
,k∈Z,φ=
+kπ,k∈Z.
因为|φ|<
,所以φ=
,
所以f(x)=3sin
.
由-
+2kπ≤2x+
≤
+2kπ得-
+kπ≤x≤
+kπ,k∈Z,即f(x)的单调递增
区间为
k∈Z.
答案:
,k∈Z
14.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示,其中
|PQ|=2
.则f(x)的解析式为________.?
【解析】由题图可知A=2,P(x1,-2),Q(x2,2),
所以|PQ|=
整理得|x1-x2|=2,所以函数f(x)的最小正周期T=2|x1-x2|=4,即
=4,
解得ω=
.又函数图象过点(0,-
),
所以2sin
φ=-
,即sinφ=-
.又|φ|<
,
所以φ=-
,所以f(x)=2sin
答案:f(x)=2sin
【加练备选】
已知函数f(x)=4cos(ωx+φ)(ω>0,0<φ<π)为奇函数,A(a,0),
B(b,0)是其图象上两点,若|a-b|的最小值是1,则f
=________.
【解析】因为函数f(x)=4cos(ωx+φ)(ω>0,0<φ<π)为奇函数,
所以φ=
,f(x)=-4sin
ωx.
因为A(a,0),B(b,0)是其图象上两点,
|a-b|的最小值是1,所以
=1,
所以ω=π,f(x)=-4sin
πx,
则f
=-4sin
=-2.
答案:-2
三角函数的图象与性质
关键能力·应用实践
考向一 三角函数的定义、诱导公式及同角三角函数基本关系
【多维题组】速通关
1.(2020·北京高考)2020年3月14日是全球首个国际圆周率日(πDay).历史上,求圆周率π的方法有多种,与中国传统数学中的“割圆术”相似,数学家阿尔·卡西的方法是:当正整数n充分大时,计算单位圆的内接正6n边形的周长和外切正6n边形(各边均与圆相切的正6n边形)的周长,将它们的算术平均数作为2π的近似值,按照阿尔·卡西的方法,π的近似值的表达式是( )
【解析】选A.对于内接多边形,将其分割为三角形,如图①,在△OPQ中,O是圆心,
半径OP为1,OM为PQ边上的高,
,所以在Rt△POM中,
所以边长
,
周长
对于外切多边形,将其分割为三角形,如图②,在△OPQ中O是圆心,半径OM为1,OM
为PQ边上的高,
,所以在Rt△POM中,
所以边长
,周长为6nPQ=12n·tan
.
综上,2π的近似值为
(12n·sin
+12n·tan
)=6n(sin
+tan
),π的
近似值为3n(sin
+tan
).
2.若tan
α=
,则sin4α+cos4α的值为________.?
【解析】因为tan
α=
,所以
所以sin4α+cos4α=(sin2α+cos2α)2-2sin2αcos2α
=1-2×
=
.
答案:
3.已知函数f(x)=ax-2+2(a>0且a≠1)过定点P,且角α的始边与x轴的正半轴重合,
终边过点P,则
=______.?
【解析】函数f(x)=ax-2+2(a>0且a≠1)过定点P(2,3),
则tan
α=
.
答案:
【变式拓展】
本题函数改为f(x)=loga(x+4)+2(a>0且a≠1),其他条件不变,则sin
sin(3π+α)=________.?
【解析】函数f(x)=loga(x+4)+2(a>0且a≠1)的图象恒过点P(-3,2),则
sin
α=
,cos
α=-
,
所以sin
sin(3π+α)
=sin
sin(π+α)=-cos
αsin
α=
.
答案:
4.(2020·南昌三模)已知sin
则
=________.?
【解析】因为
所以
答案:
【技法点拨】提素养
1.三角函数:设α是一个任意角,它的终边与单位圆交于点P(x,y),则
sin
α=y,cos
α=x,tan
α=
(x≠0).各象限角的三角函数值的符号:一全正,
二正弦,三正切,四余弦.
2.利用诱导公式进行化简求值的步骤
利用诱导公式化任意角的三角函数为锐角三角函数,其步骤:去负—脱周—化锐.
特别注意函数名称和符号的确定.
提醒:“奇变偶不变,符号看象限”.
考向二 三角函数的图象
【多维题组】速通关
1.要想得到函数y=sin
2x+1的图象,只需将函数y=cos
2x的图象( )
A.向左平移
个单位长度,再向上平移1个单位长度
B.向右平移
个单位长度,再向上平移1个单位长度
C.向左平移
个单位长度,再向下平移1个单位长度
D.向右平移
个单位长度,再向下平移1个单位长度
【解析】选B.先将函数y=cos
2x=sin
的图象向右平移
个单位长度,得
到y=sin
2x的图象,再向上平移1个单位长度,即得y=sin
2x+1的图象.
【变式拓展】
本题“y=sin
2x+1”改为“y=cos
”,“y=cos
2x”改为“y=sin
2x”,
如何进行图象变换.
【解析】因为y=cos
=sin
=sin
2
所以将函数y=sin
2x的图象向左平移
个单位长度可得到函数y=cos
的图象.
2.已知函数y=
sin
2x的图象与函数y=3cos
2x的图象相邻的三个交点分别是
A,B,C,则△ABC的面积为( )
A.
B.
C.
D.
【解析】选B.函数y=
sin
2x的图象与函数y=3cos
2x的图象的交点为(x,y),
令
sin
2x=3cos
2x,故tan
2x=
,
解得2x=
+kπ(k∈Z),不妨令2x=
,
,
,
所以x=
,
,
,
即
所以三角形的底边长为π,高为
=3.
S△ABC=
×π×3=
π.
3.(2020·浙江高考)函数y=xcos
x+sin
x在区间[-π,π]的图象大致为( )
【解析】选A.-xcos
(-x)+sin
(-x)=-xcos
x-sin
x,故y=xcos
x+sin
x为奇函数,排除C,D选项,当x=π时,y=-π,故选A.
4.(2020·新高考全国Ⅰ卷)如图是函数y=sin(ωx+φ)的部分图象,则
sin(ωx+φ)=( )
【解析】选BC.令f(x)=y=sin(ωx+φ),由图象得
,所以
解得|ω|=2,故A项错误;将
代入f(x)=sin(2x+φ),得2×
+φ=kπ(k∈Z),
得φ=-
+kπ(k∈Z),令k=1,则φ=
所以f(x)=sin
即
,故C正确;由sin
α=sin(π-α),得f(x)=
sin
,故B正确;由f(0)>0,排除D.故选B,C.
【技法点拨】提素养
1.关于三角函数的图象变换的方法
(1)平移变换
①沿x轴平移:由y=f(x)变为y=f(x+φ)时,“左加右减”,即φ>0,左移;φ<0,右移.
②沿y轴平移:由y=f(x)变为y=f(x)+k时,“上加下减”,即k>0,上移;k<0,下移.
(2)伸缩变换
①沿x轴伸缩:由y=f(x)变为y=f(ωx)时,点的纵坐标不变,横坐标变为原来的
倍.
②沿y轴伸缩:由y=f(x)变为y=Af(x)时,点的横坐标不变,纵坐标变为原来的|A|
倍.
2.根据图象求解析式y=Asin
(ωx+φ)+k(A>0,ω>0)的方法
(1)在一个周期内(或者从最高点到相邻的最低点,即半个周期内),若最大值为M,
最小值为m,则A=
,k=
.特别地,当k=0时,A=M=-m.
(2)φ的求法通常有以下两种:
①代入法:把图象上的一个已知点代入(此时,A,ω,k已知),或代入图象与直线
y=k的交点求解(此时要注意交点在上升区间还是下降区间).
②五点法:确定φ值时,往往以寻找“五点法”中的零点
作为突破口,具
体如下:
“第一点”(即图象上升时与y=k的交点中距原点最近的交点)为ωx+φ=0;“第
二点”(即图象的“峰点”)为ωx+φ=
;“第三点”(即图象下降时与y=k的交
点)为ωx+φ=π;“第四点”(即图象的“谷点”)为ωx+φ=
;“第五点”为
ωx+φ=2π.
考向三 三角函数的性质(重难突破)
【多维题组】速通关
1.(2020·天津高考)已知函数f(x)=sin
.给出下列结论:
①f(x)的最小正周期为2π;
②
是f(x)的最大值;
③把函数y=sin
x的图象上所有点向左平移
个单位长度,可得到函数y=f(x)的
图象.
其中所有正确结论的序号是( )
A.①
B.①③
C.②③
D.①②③
【解析】选B.因为f(x)=sin
,所以最小正周期T=
=2π,故①正确;
故②不正确;将函数y=sin
x的图象上所有点向左平
移
个单位长度,
得到y=sin
的图象,故③正确.
2.将函数f(x)=cos
x的图象向右平移
π个单位长度,再将各点的横坐标变为原
来的
(ω>0),得到函数g(x)的图象,若g(x)在
上的值域为
则ω的范
围为( )
A.
B.
C.
D.
【考场思维】
解题方法
数形结合
整体代换
y=Acos(ωx+φ),令t=ωx+φ转化为y=Acos
t,根据条件结合图象列不等式
素养考查
数学运算、逻辑推理
【解析】选A.将函数f(x)=cos
x的图象向右平移
π个单位长度,可得
y=cos
的图象;
再将各点的横坐标变为原来的
(ω>0),
得到函数g(x)=cos
的图象.
若g(x)在
上的值域为
此时,
令t=ωx-
,则问题转化为y=cos
t,
在
上的值域为
结合图象可知,0≤
≤
,求得
≤ω≤
.
【加练备选】
已知函数f(x)=cos
,把y=f(x)的图象向左平移
个单位长度得到函数g(x)
的图象,则下列说法正确的是( )
A.
B.g(x)的图象关于直线
对称
C.g(x)的一个零点为
D.g(x)的一个单调减区间为
【考场思维】
解题方法
整体代换
结论应用
图象变换强调对自变量x本身的变换,
余弦型函数的对称轴和对称中心,
复合函数单调性遵循“同增异减”
素养考查
数学运算、逻辑推理
【解析】选D.因为f(x)=cos
=cos
所以
所以
,故A错,
令
=kπ,k∈Z,
得对称轴方程为
,k∈Z,故B错,
令
,k∈Z,
得对称中心的横坐标为
,k∈Z,故C错,
因为x∈
,故μ=2x+
∈[0,π],
因为y=cos
μ在[0,π]上是减函数,故g(x)=
上是减函数,故D正确.
3.(2020·全国Ⅲ卷)关于函数f(x)=sin
x+
有如下四个命题:
①f(x)的图象关于y轴对称.
②f(x)的图象关于原点对称.
③f(x)的图象关于直线x=
对称.
④f(x)的最小值为2.
其中所有真命题的序号是________.?
【考场思维】
【解析】对于①,由sin
x≠0可得函数的定义域为
故定义域关于
原点对称,
由f(-x)=sin(-x)+
=-sin
x-
=-f(x),
所以函数为奇函数,图象关于原点对称,
①错②对.
对于③,由于f(π-x)=sin(π-x)+
=sin
x+
=f(x),所以f(x)关于x=
对称,③对.
对于④,令t=sin
x,t∈[-1,0)∪(0,1],由对勾函数g(t)=t+
的性质,可知
g(t)∈(-∞,-2]∪[2,+∞),所以f(x)无最小值,④错.
答案:②③
【技法点拨】提素养
1.求函数单调区间的方法
(1)代换法:求形如y=Asin(ωx+φ)(或y=Acos(ωx+φ))(A,ω,φ为常数,A≠0,ω>0)的单调区间时,令ωx+φ=z,得y=Asin
z(或y=Acos
z),然后由复合函数的单调性求得.
(2)图象法:画出三角函数的图象,结合图象求其单调区间.
2.判断对称中心与对称轴的方法
利用函数y=Asin(ωx+φ)的对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点这一性质,通过检验f(x0)的值进行判断.
【变式训练】
1.(2019·全国Ⅱ卷)下列函数中,以
为周期且在区间
单调递增的是( )
A.f(x)=|cos
2x|
B.f(x)=|sin
2x|
C.f(x)=cos
|x|
D.f(x)=sin
|x|
【解析】选A.作出函数f(x)=|cos
2x|的图象,如图.
由图象可知f(x)=|cos
2x|的周期为
,在区间
上单调递增.同理可得
f(x)=|sin
2x|的周期为
,在区间
上单调递减,f(x)=cos
|x|的周期为
2π.f(x)=sin
|x|不是周期函数,排除B,C,D.
2.(多选题)函数f(x)=Acos(ωx+φ)(ω>0)的部分图象如图所示,则以下结论,正
确的有( )
A.f(x)的最小正周期为2
B.f(x)图象的一条对称轴为直线x=-
C.f(x)在(2k-
,2k+
),k∈Z上是减函数
D.f(x)的最大值为A
【解析】选AC.由题图可知,函数f(x)的最小正周期
,故A正确;因
为函数f(x)的图象过点
,所以函数f(x)图象的对称轴为直线
(k∈Z),
故直线x=-
不是函数f(x)图象的对称轴,故B错误;由题图可知,当
(k∈Z),即
(k∈Z)时,f(x)是减函数,故C正
确;若A>0,则最大值是A,若A<0,则最大值是-A,故D错误.
3.(2020·包头一模)若函数f(x)=sin
2x+cos
2x在
和[3m,π]上均单调递
增,则实数m的取值范围为________.?
【解析】f(x)=
sin
解-
+2kπ≤2x+
≤
+2kπ,k∈Z得,
-
+kπ≤x≤
+kπ,k∈Z,
当k=0时,-
≤x≤
;当k=1时,
≤x≤
,
所以f(x)在
上单调递增,
又f(x)在
,[3m,π]上单调递增,
所以
解得
≤m≤
,
所以m的取值范围为
答案:
【加练备选】
(2020·南宁二模)已知函数f(x)=sin(ωx+φ)(ω≠0)的图象经过点
,一
条对称轴方程为x=
.则函数f(x)的周期可以是( )
A.
B.
C.
D.
【解析】选B.由
T,k∈Z,
则T=
,k∈Z,当k=0时,T=
.
题组训练·素养提升
【新题速递】
1.直线l:2x-y+e=0的倾斜角为α,则sin(π-α)sin
的值为( )
A.-
B.-
C.
D.
【解析】选D.因为直线l:2x-y+e=0的倾斜角为α,
所以tan
α=2,所以sin(π-α)sin
=sin
αcos
α
2.函数f(x)=2sin
+1的图象向右平移
个单位长度后得到y=g(x)的图象,
则函数g(x)( )
A.有最大值为2
B.有最小正周期为π
C.图象关于直线x=
对称
D.为奇函数
【解析】选C.由函数f(x)=2sin
+1的图象向右平移
个单位长度后得到
y=g(x)的图象,可得g(x)=f
=2sin
+1
=2sin
+1;
可得g(x)的最大值为3,故A错误;
g(x)的最小正周期T=
,故B错误;
当x=
时g(x)=
+1=3为最大值,故C对.g(-x)=2sin
+1≠-g(x),不是奇函数,故D错误.
3.(2020·全国Ⅰ卷)设函数f(x)=cos
在[-π,π]的图象大致如图,
f(x)的最小正周期为( )
【解析】选C.由题图可得,函数图象过点
,
将它代入函数f(x)可得,cos
=0,
又
是函数f(x)图象与x轴负半轴的第一个交点,
所以
所以函数f(x)的最小正周期
4.关于函数f(x)=|cos
x|+|sin
x|有下述四个结论:
①f(x)是偶函数;②f(x)在区间
上是增函数;
③f(x)的最大值为2;④f(x)的周期为
.其中所有正确结论的编号是( )
A.①②
B.①④
C.①③④
D.②③④
【解析】选B.因为f(x)=|cos
x|+|sin
x|=
①f(-x)=|cos(-x)|+|sin(-x)|=|cos
x|+|sin
x|=f(x),
所以f(x)是偶函数,所以①正确;
②f(x)的图象如图,
由图象可知f(x)在
上不单调,②错误;
③f(x)的最大值达不到2,③错误;
④因为f
=|cos
|+|sin
|
=|sin
x|+|cos
x|=f(x),
所以函数f(x)的周期为
,
所以④正确.
【创新迁移】
1.音乐,是用声音来展现美,给人以听觉上的享受.著名数学家傅立叶研究了乐声的本质,他证明了所有的乐声都能用数学表达式来描述,它们是一些形如asin
bx的简单正弦函数的和,其中频率最低的一项是基本音,其余的为泛音.由乐声的数学表达式可知,所有泛音的频率都是基本音频率的整数倍,称为基本音的谐波.下列函数中不能与函数y=0.06sin
(180
000t)构成乐声的是( )
A.y=0.02sin
(360
000t)
B.y=0.03sin
(180
000t)
C.y=0.02sin
(181
800t)
D.y=0.05sin
(540
000t)
【解析】选C.由f=
,可知若f1=nf2(n∈N
),则必有ω1=nω2(n∈N
),故选C.
2.对任意闭区间I,用MI表示函数y=cos
x在I上的最大值,若正数a满足
M[0,a]=2M[a,2a],则a的值为( )
A.
B.
C.
D.
【解析】选D.(1)当a∈
时,2a∈[0,π],
M[0,a]=1,M[a,2a]=cos
a,
由M[0,a]=2M[a,2a],得2cos
a=1,此时a=
;
(2)当a∈
时,2a∈(π,2π),M[0,a]=1,
①当a∈
时,(2a-π)-(π-a)
=3a-2π<0,M[a,2a]=cos
a,
由M[0,a]=2M[a,2a]得cos
a=
,
在a∈
上无解;
②当a∈
时,(2a-π)-(π-a)=3a-2π≥0,
M[a,2a]=cos
2a,
由M[0,a]=2M[a,2a],得2cos
2a=1,此时a=
π;
(3)当a∈
时,2a∈[2π,3π],M[0,a]=1,
M[a,2a]=1,不合题意;
(4)当a∈
时,2a∈[3π,+∞),M[0,a]=1,
M[a,2a]=1,不合题意.综上,a的值为
或
π.
专题能力提升练
一、单项选择题(共7小题,每小题5分,共35分)
1.(2020·漳州一模)若角θ的终边经过点
,则sin
+cos(π-θ)
+tan(2π-θ)=( )
A.
B.-
C.
D.-
四 三角函数的图象与性质(35分钟 70分)
【解析】选A.由题意知tan
θ=-
,
所以sin
+cos(π-θ)+tan(2π-θ)
=cos
θ-cos
θ-tan
θ=-tan
θ=
.
2.若sin
x=3sin
,则cos
xcos
=( )
A.
B.-
C.
D.-
【解析】选A.因为sin
x=3sin
,
所以sin
x=-3cos
x,所以tan
x=-3,
所以cos
xcos
=-sin
xcos
x
3.在平面直角坐标系中,
是圆x2+y2=1上的四段弧(如图),点P在其中
一段上,角α以Ox为始边,OP为终边.若tan
α
( )
A.
B.
C.
D.
【解析】选C.若P在
上,则由角α的三角函数线知,cos
α>sin
α,排除A;
若P在
上,则tan
α>sin
α,排除B;若P在
上,则tan
α>0,cos
α<0,
sin
α<0,排除D.
4.(2020·广州一模)设函数f(x)=2cos
,若对于任意的x∈R都有
f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为( )
A.
B.π
C.2π
D.4π
【解析】选C.函数f(x)=2cos
,若对于任意的x∈R,都有
f(x1)≤f(x)≤f(x2),
则f(x1)是函数的最小值,f(x2)是函数的最大值,|x1-x2|的最小值就是函数的
半个最小正周期
5.(2019·北京高考)设函数f(x)=cos
x+bsin
x(b为常数),则“b=0”是“f(x)为偶函数”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【解析】选C.因为f(x)=cos
x+bsin
x为偶函数,所以对任意的x∈R,都有
f(-x)=f(x),
即cos(-x)+bsin(-x)=cos
x+bsin
x,
所以2bsin
x=0.由x的任意性,得b=0.
故f(x)为偶函数?b=0.必要性成立.
反过来,若b=0,则f(x)=cos
x是偶函数.充分性成立.
所以“b=0”是“f(x)为偶函数”的充要条件.
6.(2018·全国卷Ⅱ)若f(x)=cos
x-sin
x在[-a,a]是减函数,则a的最大值是
( )
【解析】选A.f(x)=cos
x-sin
x=
cos
,且函数y=cos
x在区间[0,π]
上单调递减,则由
得
因为f(x)在[-a,a]上是减函数,
所以
解得a≤
,
所以0
.
7.(2020·岳阳二模)已知函数f(x)=4sin
,x∈
,若函数F(x)=f(x)-3
的所有零点依次记为x1,x2,x3,…,xn,且x1
A.
B.21π
C.
D.42π
【解题导引】零点即为曲线和x轴的交点的横坐标,所以先求出对称轴方程,在给
定区间
上有8条对称轴,由中点坐标公式可知x1+x2=
×2,以此类推,
xn-1+xn=
×2,各式相加,就可得出答案.
【解析】选C.令2x-
=
+kπ(k∈Z),可得x=
kπ+
(k∈Z),即函数的对称轴
方程为x=
kπ+
(k∈Z),又f(x)的周期T=π,令
kπ+
=
,可得k=8,所以函
数在x∈
上有8条对称轴.根据正弦函数的性质可知,x1+x2=
×2,x2+x3=
×2,…,xn-1+xn=
×2,(最后一条对称轴为函数的最大值点,应取前一条对应的
对称轴),将以上各式相加得x1+2x2+2x3+…+2xn-1+xn=
二、多项选择题(共15分,全部选对得5分,选对但不全的得3分,有选错的得0分)
8.若角A,B,C是△ABC的三个内角,则下列等式中一定成立的是( )
A.cos(A+B)=cos
C
B.sin(A+B)=-sin
C
C.cos
=sin
D.sin
=cos
【解析】选CD.因为A+B+C=π,所以A+B=π-C,
所以
cos(A+B)=cos(π-C)=-cos
C,sin(A+B)=sin(π-C)=sin
C,
9.已知函数f(x)=
则下列结论正确的是( )
A.f(x)不是周期函数
B.f(x)是奇函数
C.f(x)的图象关于直线x=
对称
D.f(x)在x=
处取得最大值
【解析】选AC.作出函数f(x)的图象如图:
则由图象知函数f(x)不是周期函数,故A正确;不是奇函数,故B错误,
若x>0,
=cos
cos
x-sin
sin
x=
(cos
x-sin
x),
=sin
cos
x-cos
sin
x
=
(cos
x-sin
x),
此时
若x≤0,
=sin
cos
x+cos
sin
x=
(cos
x+sin
x),
=cos
cos
x+sin
sin
x
=
,
此时
综上恒有
即图象关于直线x=
对称,故C正确,
当x=
时,f(x)=f
=cos
=0不是最大值,故D错误.
10.如图,已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,
)的图象与x轴交于
点E,F,与y轴交于点C,
=2
,∠OCF=
,|OE|=2,
则下列说法正确
的有( )
A.f(x)的最小正周期为6
B.
φ=-
C.f(x)的最大值为
D.
f(x)在区间(14,17)上单调递增
【解析】选CD.由题意可得:|OF|=
|OC|,
所以
|Asin
φ|=2+
,sin(2ω+φ)=0,
因为E(2,0),F
,C(0,Asin
φ).
所以
因为|ED|=
所以
把|Asin
φ|=
代入上式可得:
ω>0.
解得
=6,所以ω=
,可得周期T=
=12.
所以sin
=0,又因为
,所以φ=-
.可知:A,B不对.
所以
|Asin(-
)|=2+6,又因为A>0,所以A=
.
所以函数f(x)=
sin
,可知C正确.
x∈(14,17)时,
x-
∈
,可得:函数f(x)在(14,17)上单调递增.
综上可得:C,D正确.
三、填空题(共4小题,每小题5分,共20分)
11.已知函数f(x)=sin
ωx(0<ω<4)的图象向左平移
个单位后,关于点
对称,则实数ω的值为________.?
【解析】f(x)=sin
ωx(0<ω<4)的图象向左平移
个单位得g(x)=sin
的图象,因为g(x)的图象关于点
对称,
所以sin
=0,所以
=kπ,k∈Z,由0<ω<4知,当k=1时,
ω=2符合题意.
答案:2
12.已知f(x)=sin(ωx+φ)(ω>0,|φ|<π)在区间[2,4]上单调,且f(2)=1,
f(4)=-1,则ω=____________,f(x)在区间
上的值域是____________.?
【解析】由题意知f(x)的最小正周期T=4,
所以ω=
,所以f(x)=sin
又f(2)=sin(π+φ)=1,
所以π+φ=
+2kπ,k∈Z.
又|φ|<π,所以φ=-
,
所以f(x)=sin
由x∈
所以sin
即f(x)在区间
上的值域为
.
答案:
13.设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)与直线y=3的交点的横坐标构
成以π为公差的等差数列,且x=
是f(x)图象的一条对称轴,则φ=______,函数
f(x)的单调递增区间为________.?
【解析】由题意,得A=3,T=π,
所以ω=2,所以f(x)=3sin(2x+φ).
又f
=3或f
=-3,
所以2×
+φ=kπ+
,k∈Z,φ=
+kπ,k∈Z.
因为|φ|<
,所以φ=
,
所以f(x)=3sin
.
由-
+2kπ≤2x+
≤
+2kπ得-
+kπ≤x≤
+kπ,k∈Z,即f(x)的单调递增
区间为
k∈Z.
答案:
,k∈Z
14.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示,其中
|PQ|=2
.则f(x)的解析式为________.?
【解析】由题图可知A=2,P(x1,-2),Q(x2,2),
所以|PQ|=
整理得|x1-x2|=2,所以函数f(x)的最小正周期T=2|x1-x2|=4,即
=4,
解得ω=
.又函数图象过点(0,-
),
所以2sin
φ=-
,即sinφ=-
.又|φ|<
,
所以φ=-
,所以f(x)=2sin
答案:f(x)=2sin
【加练备选】
已知函数f(x)=4cos(ωx+φ)(ω>0,0<φ<π)为奇函数,A(a,0),
B(b,0)是其图象上两点,若|a-b|的最小值是1,则f
=________.
【解析】因为函数f(x)=4cos(ωx+φ)(ω>0,0<φ<π)为奇函数,
所以φ=
,f(x)=-4sin
ωx.
因为A(a,0),B(b,0)是其图象上两点,
|a-b|的最小值是1,所以
=1,
所以ω=π,f(x)=-4sin
πx,
则f
=-4sin
=-2.
答案:-2
同课章节目录
