数列高考小题等差数列等比数列课件2021届高考数学二轮(共PPT83张)
文档属性
| 名称 | 数列高考小题等差数列等比数列课件2021届高考数学二轮(共PPT83张) |  | |
| 格式 | ppt | ||
| 文件大小 | 917.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 22:15:34 | ||
图片预览




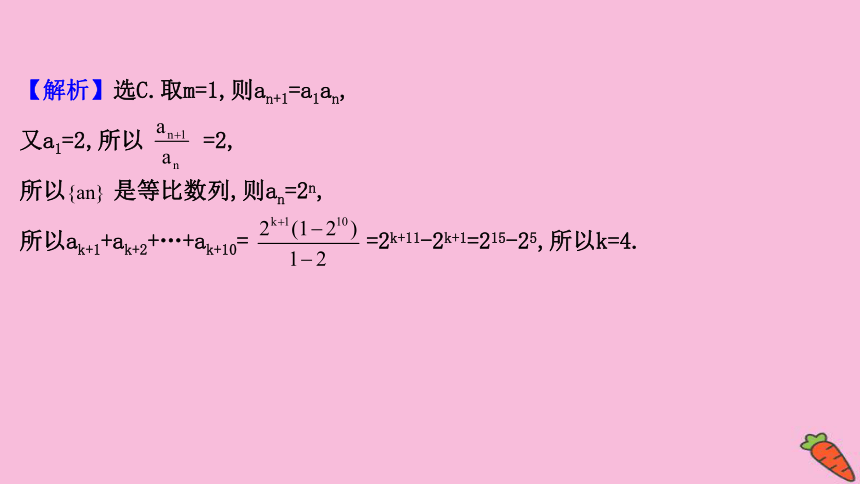





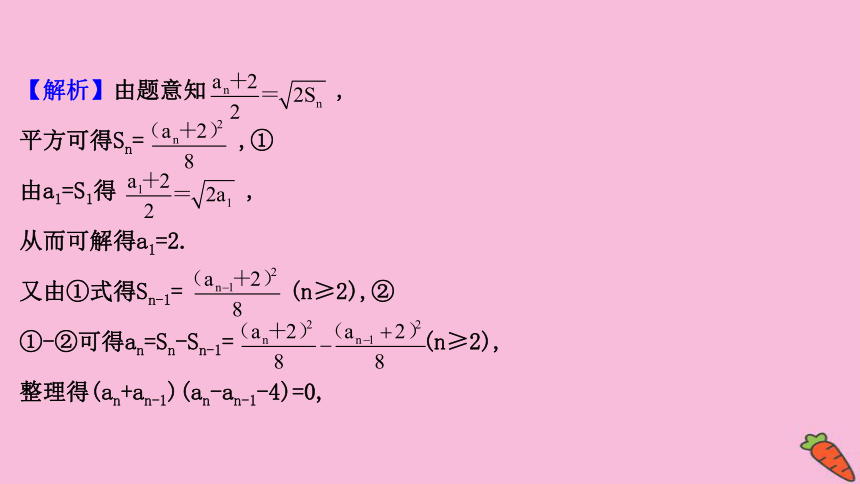

文档简介
(共83张PPT)
数列高考小题
等差数列、等比数列
关键能力·应用实践
考向一 等差、等比数列的基本量计算
【多维题组】速通关
1.已知p:数列{an}是等差数列,q:数列{an}的通项公式an=k1n+k2(k1,k2均为常数),
则p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【解析】选C.若{an}是等差数列,不妨设公差为d.
所以an=a1+(n-1)d=dn+a1-d,
令k1=d,k2=a1-d,则an=k1n+k2,
若数列{an}的通项公式an=k1n+k2(k1,k2为常数,n∈N
),
则当n≥2且n∈N
时,an-1=k1(n-1)+k2,
所以an-an-1=k1(常数)(n≥2且n∈N
),
所以{an}为等差数列,所以p是q的充要条件.
2.(2020·全国Ⅱ卷)数列
中,a1=2,am+n=aman,若ak+1+ak+2+…+ak+10=215-25,则
k=( )
A.2
B.3
C.4
D.5
【解析】选C.取m=1,则an+1=a1an,
又a1=2,所以
=2,
所以
是等比数列,则an=2n,
所以ak+1+ak+2+…+ak+10=
=2k+11-2k+1=215-25,所以k=4.
3.(2020·北京高考)在等差数列{an}中,a1=-9,a5=-1.记Tn=a1a2…an(n=1,2,…),
则数列{Tn}( )
A.有最大项,有最小项
B.有最大项,无最小项
C.无最大项,有最小项
D.无最大项,无最小项
【解析】选B.设公差为d,因为a1=-9,a5=a1+4d=-1,所以d=2,所以
a1,…,a5<0,a6,…>0,所以T1<0,T2>0,T3<0,T4>0,T5<0,以后都小于0,且越来越小.
4.(2020·全国Ⅱ卷)记Sn为等差数列{an}的前n项和.若a1=-2,a2+a6=2,则S10=________.?
【解析】设等差数列{an}的公差为d.
因为{an}是等差数列,且a1=-2,a2+a6=2,
根据等差数列通项公式:an=a1+
d,
可得a1+d+a1+5d=2,即-2+d+(-2)+5d=2,
整理可得:6d=6,解得:d=1.
根据等差数列前n项和公式:Sn=na1+
d,n∈N
,
可得:S10=10×(-2)+
=-20+45=25,
所以S10=25.
答案:25
5.已知正项数列{an}的前n项和Sn满足:Sn和2的等比中项等于an和2的等差中项,则
a1=________,Sn=________.?
【解析】由题意知
,
平方可得Sn=
,①
由a1=S1得
,
从而可解得a1=2.
又由①式得Sn-1=
(n≥2),②
①-②可得an=Sn-Sn-1=
(n≥2),
整理得(an+an-1)(an-an-1-4)=0,
因为数列{an}的各项都是正数,
所以an-an-1-4=0,即an-an-1=4.
故数列{an}是以2为首项4为公差的等差数列,
所以Sn=2n+
×4=2n2.
当n=1时,S1=a1=2.
故Sn=2n2.
答案:2 2n2
【技法点拨】提素养
等差、等比数列基本运算的关注点
(1)基本量:在等差(比)数列中,首项a1和公差d(公比q)是两个基本元素;
(2)解题思路:①设基本量a1和d(q);②列、解方程(组);把条件转化为关于a1和
d(q)的方程(组),然后求解,注意整体计算,减少计算量.
考向二 求数列的通项
【多维题组】速通关
1.(2020·临沂二模)已知数列{an}中,a1=1,an+1=
,则数列{an}的通项公式
an=________.?
【解析】因为an+1=
,a1=1,
所以an≠0,
所以
,即
.
又a1=1,则
=1,所以
是以1为首项,
为公差的等差数列.
所以
.
所以an=
(n∈N
).
答案:
2.已知数列{an}满足an+2=an+1-an,且a1=2,a2=3,则a2
021的值为________.?
【解析】由题意得,a3=a2-a1=1,a4=a3-a2=-2,a5=a4-a3=-3,a6=a5-a4=-1,a7=a6-
a5=2,a8=a7-a6=3,…,所以数列{an}是周期为6的周期数列,而2
021=6×336+5,所
以a2
021=a5=-3.
答案:-3
【变式拓展】
本题条件不变,设数列{an}的前n项和为Sn,则S2
021=________.?
【解析】由题意得,a3=a2-a1=1,a4=a3-a2=-2,a5=a4-a3=-3,a6=a5-a4=-1,a7=a6-
a5=2,a8=a7-a6=3,…,所以数列{an}是周期为6的周期数列,S6=a1+a2+a3+a4+a5+a6=0,
而2
021=6×336+5,所以S2
021=S5=1.
答案:1
3.设等比数列{an}满足a1+a3=10,a2+a4=5,则a1a2·…·an的最大值为________.
【解析】由于{an}是等比数列,设an=a1qn-1,其中a1是首项,q是公比.
所以
?
解得:
故an=
,
所以a1·a2·…·an=
=
.
当n=3或4时,
取到最小值-6,
此时
取到最大值26.
所以a1·a2·…·an的最大值为64.
答案:64
4.在数列{an}中,若a1=1,an+1=2an+3(n≥1),则该数列的通项公式an=________.?
【解析】方法一:(递推法)
an=2an-1+3=2(2an-2+3)+3=22·an-2+2×3+3
=23an-3+22×3+2×3+3=…
=2n-1·a1+2n-2·3+2n-3·3+…+3
=2n-1+3(2n-2+2n-3+…+1)=2n+1-3.
方法二:(构造法)
设an+a=2(an-1+a)(n≥2,n∈N
),
即an=2an-1+a,所以a=3.
所以an+3=2(an-1+3),
所以{an+3}是公比为2的等比数列.
所以an+3=(a1+3)·2n-1.
又a1=1,所以an=2n+1-3.
答案:2n+1-3
【技法点拨】提素养
求数列通项公式的常用方法
(1)公式法:①等差数列的通项公式;②等比数列的通项公式.
(2)已知Sn(a1+a2+…+an=Sn),求an,用作差法:
an=
(3)已知a1·a2·…·an=f(n),an≠0,求an,用作商法:
an=
(4)已知an+1-an=f(n),求an,用累加法:an=(an-an-1)+(an-1-an-2)+…+(a2-
a1)+a1=f(n-1)+f(n-2)+…+f(1)+a1(n≥2).
(5)已知
=f(n),求an,用累乘法:an=
·
·…·
·a1=f(n-1)·f(n-
2)·…·f(1)·a1(n≥2).
(6)构造等比数列法:若已知数列{an}中,an+1=pan+q(p≠0,p≠1,q≠0),a1≠
,
设存在非零常数λ,使得an+1+λ=p(an+λ),其中λ=
,则数列
就是
以a1+
为首项,p为公比的等比数列,先求出数列
的通项公式,再
求出数列{an}的通项公式即可.
(7)倒数法:若an=
(mkb≠0,n≥2),对an=
取倒数,得到
,即
.令bn=
,则{bn}可归纳为
bn+1=pbn+q(p≠0,p≠1,q≠0)型.
考向三 等差、等比数列性质综合
【多维题组】速通关
1.设等差数列{an}的前n项和为Sn,a2+a4=6,则S5等于( )
A.10
B.12
C.15
D.30
【解析】选C.由等差数列的性质可得a2+a4=a1+a5,
所以S5=
=15.
【变式拓展】
若本题再添加条件a6=9,试求该数列的前n项和Sn.
【解析】设等差数列{an}的公差为d,因为a2+a4=6,且数列为等差数列,所以a3=3,
又因为a6=9,所以公差d=2,a1=-1,其前n项和Sn=n(-1)+
×2=n2-2n.
2.(多选)设等比数列{an}的公比为q,则下列结论正确的是( )
A.数列{anan+1}是公比为q2的等比数列
B.数列{an+an+1}是公比为q的等比数列
C.数列{an-an+1}是公比为q的等比数列
D.数列
是公比为
的等比数列
【解析】选AD.对于A,由
=q2(n≥2)知数列{anan+1}是公比为q2的等比数列;
对于B,当q=-1时,数列{an+an+1}的项中有0,不是等比数列;对于C,当q=1时,数列
{an-an+1}的项中有0,不是等比数列;对于D,
,所以数列
是公比为
的等比数列.
3.(2020·全国Ⅱ卷)
北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.
上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一
环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环
依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石
板(不含天心石)( )
A.3
699块
B.3
474块
C.
3
402块
D.3
339块
【解析】选C.设每一层有n环,由题可知从内到外每环的扇面形石板数之间构成
等差数列
,且公差d=9,首项a1=9,由等差数列的性质可知Sn,S2n-Sn,S3n-S2n成等
差数列,且
=n2d,
由题意得9n2=729,所以n=9,则三层共有扇面
形石板为S3n=S27=27a1+
×9=3
402(块).
4.已知等比数列{an}的公比q>0,前n项和为Sn,若2a3,a5,3a4成等差数列,a2a4a6=64,
则q=________,Sn=________.?
【解析】由2a3,a5,3a4成等差数列得2a5=2a3+3a4?2q2=2+3q?q=2(负值舍
去),a2a4a6=64?
=64?a4=4?a1=
,Sn=
.
答案:2
【技法点拨】提素养
等差、等比数列性质问题的求解策略
(1)抓住项与项之间的关系及项与序号之间的关系,从这些特点入手选择恰当的
性质进行求解.
(2)数列是一种特殊的函数,具有函数的一些性质,如单调性、周期性等,可利用
函数的性质解题.
(3)利用数列性质进行运算时,要利用整体思想,可以减少计算量,此方法还适用
于求函数值、求函数的解析式等问题.
【加练备选】
纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采
用国际标准,规定以A0、A1、A2、B1、B2等标记来表示纸张的幅面规格.复印纸
幅面规格只采用A系列和B系列,其中系列的幅面规格为:①A0、A1、A2、…、A8
所有规格的纸张的幅宽(以x表示)和长度(以y表示)的比例关系都为x∶y=1∶
;
②将A0纸张沿长度方向对开成两等份,便成为A1规格,A1纸张沿长度方向对开成
两等份,便成为A2规格,…,如此对开至A8规格.现有A0、A1、A2、…、A8纸各一
张.若A4纸的宽度为2
dm,则A0纸的面积为________dm2;这9张纸的面积之和等于
________dm2.?
【解析】可设Ai
的纸张的长度为ai+1,面积为Si+1,Ai的幅宽为
ai+1,
A
的长度为ai+2=
ai+1,
所以,数列
是以
为公比的等比数列,
由题意知A4纸的宽度为
a5=2,所以a5=2
,
所以a1=
,所以A0纸的面积为S1=
(dm2).
又Sn=
,所以
,所以,数列
是以64
为
首项,以
为公比的等比数列,因此,这9张纸的面积之和等于
(dm2).
答案:64
题组训练·素养提升
【新题速递】
1.等比数列
的前n项和为Sn,若a1+a2+a3=3,a4+a5+a6=6,则S12=( )
A.15
B.30
C.45
D.60
【解析】选C.由题意,等比数列
的前n项和为Sn,
满足a1+a2+a3=3,a4+a5+a6=6,
则
,
所以a7+a8+a9=12,a10+a11+a12=24,
则S12=a1+a2+a3+…+a10+a11+a12=45.
2.已知等差数列
的前n项和为Sn,且a1,
,a4成公比为q的等比数列,则q等于
( )
A.1或2
B.2
C.1
D.2或4
【解析】选A.因为a1,
,a4成公比为q的等比数列,
所以
=a1·a4,
又因为
为等差数列,
设等差数列{an}的公差为d,
所以
=a1·a4,
所以
=a1·
,即
=0,
即d=0或d=a1.
所以q=
=1或q=
=2.
3.(2020·泰安二模)若等比数列{an}的各项均为正数,且a10a11+a9a12=2e5,则
ln
a1+ln
a2+…+ln
a20=________.?
【解析】因为a10a11+a9a12=2a10a11=2e5,
所以a10a11=e5.
所以ln
a1+ln
a2+…+ln
a20
=ln(a1a2…a20)
=ln[(a1a20)·(a2a19)·…·(a10a11)]
=ln(a10a11)10=10ln(a10a11)
=10ln
e5=50ln
e=50.
答案:50
4.已知数列
满足:对任意n∈N
均有an+1=pan+2p-2(p为常数,p≠0且p≠1),若
a2,a3,a4,a5∈{-18,-6,-2,6,11,30},则a1的所有可能取值的集合是________.?
【解析】因为an+1=pan+2p-2,
所以an+1+2=p(an+2),
所以①若a1=-2,则a1+1+2=p(a1+2)=0,a2=-2,同理可得,a3=a4=a5=-2,即a1=-2符合题
意;
②若a1≠-2,p为不等于0与1的常数,则数列{an+2}是以p为公比的等比数列,
因为ai∈{-18,-6,-2,6,11,30},i=2,3,4,5,
an+2可以取-16,-4,8,32,所以若|p|>1,
则p=-2,由a2+2=-4=-2(a1+2)得:a1=0;
若|p|<1,则p=-
,由a2+2=32=-
(a1+2)得:a1=-66.
综上所述,满足条件的a1的所有可能取值为-2,0,-66.
答案:
【创新迁移】
1.如图,点列{An},{Bn}分别在某锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N
,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N
(P≠Q表示
点P与Q不重合).若dn=|AnBn|,Sn为△AnBnBn+1的面积,则下列结论正确的是( )
A.{Sn}是等差数列
B.{
}是等差数列
C.{dn}是等差数列
D.{
}是等差数列
【解析】选A.由题意,过点A1,A2,A3,…,An,An+1,…分别作直线B1Bn+1的垂线,高分
别记为h1,h2,h3,…,hn,hn+1,…,根据平行线的性质,得h1,h2,h3,…,hn,hn+1,…成等
差数列,又Sn=
×|BnBn+1|×hn,|BnBn+1|为定值,所以{Sn}是等差数列.
2.已知数列{an}的前m(m≥4)项是公差为2的等差数列,从第m-1项起,
am-1,am,am+1,…成公比为2的等比数列.若a1=-2,则m=________,{an}的前6项和
S6=________.?
【解析】由a1=-2,公差d=2,
得am-1=-2+2(m-2)=2m-6,
am=-2+2(m-1)=2m-4,则
=2,
所以m=4;
所以S6=a1+a2+a3+a4+a5+a6
=-2+0+2+4+8+16=28.
答案:4 28
专题能力提升练
七 等差数列、等比数列
(40分钟 80分)
一、单项选择题(共8小题,每小题5分,共40分)
1.(2020·菏泽二模)已知等比数列{an}的公比为正数,且a3a9=2
,则公比
q=( )
A.
B.
C.
D.2
【解析】选C.a3a9=
因为q>0,所以q=
.
2.(2019·全国Ⅲ卷)已知各项均为正数的等比数列{an}的前4项的和为15,且a5=3a3+4a1,则a3=( )
A.16
B.8
C.4
D.2
【解析】选C.设该等比数列的首项为a1,公比为q,
由已知得,a1q4=3a1q2+4a1,
因为a1>0且q>0,则可解得q=2,
又因为a1(1+q+q2+q3)=15,
即可解得a1=1,则a3=a1q2=4.
3.设Sn为等差数列{an}的前n项和,若
则
=( )
【解析】选A.设公差为d,则
所以
4.已知数列{an}为等比数列,a4+a7=2,a5a6=-8,则a1+a10=( )
A.7
B.5
C.-5
D.-7
【解析】选D.设数列{an}的公比为q.由题意,得
所以
或
解得
或
当
时,a1+a10=a1(1+q9)=1+(-2)3=-7;
当
时,a1+a10=a1(1+q9)=(-8)×
=-7.
综上,a1+a10=-7.
5.已知等比数列{an}公比为q,其前n项和为Sn,若S3,S9,S6成等差数列,则q3等于
( )
A.-
B.1
C.-
或1
D.-1或
【解析】选A.若q=1,则3a1+6a1=2×9a1,
得a1=0,矛盾,故q≠1.
所以
解得q3=-
或1(舍).
6.等差数列{an}中,已知|a6|=|a11|,且公差d>0,则其前n项和取最小值时n的值为
( )
A.6
B.7
C.8
D.9
【解析】选C.由d>0可得等差数列{an}是递增数列,又|a6|=|a11|,
所以-a6=a11,即-a1-5d=a1+10d,
所以a1=-
,则a8=-
<0,a9=
>0,
所以前8项和为前n项和的最小值,故选C.
7.已知数列{an}的前n项和为Sn,且a1=2,an+1=Sn,若an∈(0,2
020),则称项an为
“和谐项”,则数列{an}的所有“和谐项”的平方和为( )
A.
×411+
B.
×411-
C.
×410+
D.
×412-
【解析】选A.因为an+1=Sn,
所以an=Sn-1(n≥2),
则an+1-an=Sn-Sn-1,
即an+1-an=an,an+1=2an,
=2,
因为a1=2,所以a2=S1=a1=2,
故an=
因为an∈(0,2
020),所以1≤n≤11,数列{an}的所有“和谐项”的平方和为
8.已知a1,a2,a3,a4依次成等比数列,且公比q不为1,将此数列删去一个数后得到的数列(按原来的顺序)是等差数列,则正数q的值是( )
【解析】选B.因为公比q不为1,所以删去的数不是a1,a4.
①若删去a2,则由2a3=a1+a4得2a1q2=a1+a1q3,又a1≠0,所以2q2=1+q3,
整理得q2(q-1)=(q-1)(q+1).
又q≠1,所以q2=q+1,
又q>0,得q=
;
②若删去a3,
则由2a2=a1+a4得2a1q=a1+a1q3,
又a1≠0,所以2q=1+q3,
整理得q(q+1)(q-1)=q-1.
又q≠1,则可得q(q+1)=1,
又q>0,得q=
.
综上所述,q=
.
二、多项选择题(共20分,全部选对得5分,选对但不全的得3分,有选错的得0分)
9.记单调递增的等比数列{an}的前n项和为Sn,若a2+a4=10,a2a3a4=64,则( )
A.Sn+1-Sn=2n+1
B.an=2n-1
C.Sn=2n-1
D.Sn=2n-1-1
【解析】选BC.由a2a3a4=64得
=43,则a3=4.
设等比数列{an}的公比为q(q≠0),
由a2+a4=10,得
+4q=10,
即2q2-5q+2=0,解得q=2或q=
.
又因为数列{an}单调递增,所以q=2,
所以2a1+8a1=10,解得a1=1.
所以an=2n-1,Sn=
=2n-1,
所以Sn+1-Sn=2n+1-1-(2n-1)=2n.
10.数列{Fn}:1,1,2,3,5,8,13,21,34,…称为斐波那契数列,是由十三世纪意大利数学家列昂纳多·斐波那契以兔子繁殖为例子而引入的,故又称为“兔子数列”.该数列从第三项开始,每项等于其前相邻两项之和.记数列{Fn}的前n项和为Sn,则下列结论正确的是( )
A.S5=F7-1
B.S5=S6-1
C.S2
019=F2
021-1
D.S2
019=F2
020-1
【解析】选AC.根据题意有Fn=Fn-1+Fn-2(n≥3),
所以S3=F1+F2+F3=1+F1+F2+F3-1=F3+F2+F3-1=F4+F3-1=F5-1,S4=F4+S3=F4+F5-1=F6-1,S5=F5+S4=F5+F6-1=F7-1,
…
所以S2
019=F2
021-1.
11.等差数列{an}是递增数列,满足a7=3a5,前n项和为Sn,下列选择项正确的是( )
A.d>0
B.a1<0
C.当n=5时Sn最小
D.Sn>0时n的最小值为8
【解析】选ABD.由题意,设等差数列{an}的公差为d,因为a7=3a5,可得
a1+6d=3(a1+4d),解得a1=-3d,又由等差数列{an}是递增数列,可知d>0,则a1<0,故
A,B正确;因为
由
可知,当n=3或4时Sn最
小,故C错误,令Sn=
n2-
n>0,解得n<0或n>7,即Sn>0时n的最小值为8,故D正确.
12.已知数列{an}是各项均为正数的等比数列,{bn}是公差不为0的等差数列,且a2=b2,a8=b8,则( )
A.a5=b5
B.a5C.a4D.a6>b6
【解析】选BC.方法一:设{an}的公比为q(q>0),{bn}的公差为d(d≠0).
a5=
,b5=
,
由基本不等式得
≤
,
当且仅当a2=a8时等号成立.
易知数列{bn}不是常数列,故B正确,A错误.
因为a2·q6=a8=b8=b2+6d=a2+6d,
所以d=
,
所以a4-b4=a2q2-(b2+2d)=a2q2-a2-2d=a2
=
(3q2-q6-2)=
(q2-
q6+2q2-2)=
[(1-q2)(q4+q2-2)]
=-
(1-q2)2(q2+2)<0,a6-b6=a2q4-a2-4d=
(3q4-1-2q6)=-
(1-q2)2(2q2+1)<0.
故C正确,D错误.
方法二:设{an}的公比为q(q>0),{bn}的公差为d(d≠0).
an=a1qn-1=
·qn,
bn=b1+(n-1)d=b1-d+nd,
将其分别理解成关于n的类指数函数(指数函数的图象为下凹曲线)和一次函数
(一次函数的图象为直线),则两函数图象在n=2,n=8处相交,故an而a4【加练备选】
若正项数列{an}满足an+1=an-ln
an,0Tn=a1·a2·a3·…·an,n∈N
,则下列说法正确的是( )
A.对任意的n∈N
,恒有an+1≥1
B.对任意的n∈N
,恒有Sn>n
C.对任意的n∈N
,恒有0D.对任意的n∈N
,恒有Sn≥Tn
【解析】选ACD.设函数f(x)=x-ln
x(x>0),则f′(x)=1-
=
,
所以函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,故f(x)min=f(1)=1.
又an+1=an-ln
an,所以an+1≥1,A正确;
因为0因为an+1=an-ln
an,所以an-an+1=ln
an,
所以a1-an+1=(a1-a2)+(a2-a3)+…+(an-an+1)
=ln
a1+ln
a2+…+ln
an
=ln(a1·a2·…·an)<0,
故a1·a2·…·an<1,即0又当n≥2时,Sn>n-1≥1,故Sn≥Tn,D正确.
三、填空题(共4小题,每小题5分,共20分)
13.(2020·全国Ⅰ卷)数列{an}满足an+2+(-1)nan=3n-1,前16项和为540,则
a1=________.?
【解析】an+2+(-1)nan=3n-1,
当n为奇数时,an+2=an+3n-1;
当n为偶数时,an+2+an=3n-1.
设数列
的前n项和为Sn,
S16=a1+a2+a3+a4+…+a16
=a1+a3+a5+…+a15+(a2+a4)+…+(a14+a16)
=a1+(a1+2)+(a1+10)+(a1+24)+(a1+44)+(a1+70)
+(a1+102)+(a1+140)+(5+17+29+41)
=8a1+392+92=8a1+484=540,
所以a1=7.
答案:7
【加练备选】
设{an}是公差不为零的等差数列,Sn为其前n项和,已知S1,S2,S4成等比数列,且a3=5,则数列{an}的通项公式为________.?
【解析】设数列{an}的公差为d(d≠0),因为{an}是等差数列,S1,S2,S4成等比数列,所以(a1+a2)2=a1(a1+a2+a3+a4),因为a3=5,所以(5-2d+5-d)2=(5-2d)(5-2d+15),解得d=2或d=0(舍去),所以5=a1+(3-1)×2,即a1=1,所以an=2n-1.
答案:an=2n-1
14.设等比数列{an}的前n项和为Sn,满足对任意的正整数n,均有Sn+3=8Sn+3,则
a1=________,公比q=________.?
【解析】由Sn+3=8Sn+3,则Sn+2=8Sn-1+3,
两式相减得,an+3=8an?anq3=8an,
则q3=8?q=2,
由等比数列前n项和公式得,
即2n+3a1-a1=8·2na1-8a1+3,
从而解得a1=
.
答案:
2
【加练备选】
已知数列{an}的前n项和Sn=n2+2n-1(n∈N
),则a1=________;数列{an}的通项公式
为an=________.?
【解析】因为Sn=n2+2n-1,
当n=1时,a1=1+2-1=2,
当n≥2时,an=Sn-Sn-1=n2+2n-1-[(n-1)2+2(n-1)-1]=2n+1,a1=2不满足an=2n+1,所
以an=
答案:2
15.已知数列{an}的通项公式an=-n2+10n-21,前n项和为Sn,若n>m,则Sn-Sm的最大值是________.?
【解析】数列{an}的通项公式an=-n2+10n-21=-(n-3)(n-7),当3≤n≤7时,an≥0,当n≤2或n≥8时,an<0,Sn最大值为S6或S7,Sm最小值为S2或S3,Sn-Sm的最大值为S6-S3=a4+a5+a6=3+4+3=10.
答案:10
16.已知数列{an}满足a1=
,an=
(n≥2,n∈N
),则通项公式
an=________.?
【解析】由
令
=bn,则bn=
·bn-1+
?bn-
1=
·(bn-1-1),由a1=
,得b1-1=-
,所以{bn-1}是以-
为首项,
为公比
的等比数列,所以bn-1=
得
答案:
【加练备选】
数列{an}中,前n项和为Sn,a1=1,an+1=Sn+3n(n∈N
,n≥1),则数列{Sn}的通项公式为
________.?
【解析】因为an+1=Sn+3n=Sn+1-Sn,所以Sn+1=2Sn+3n,所以
所以
又
所以数列
是首项为-
,公比为
的等比数列,
所以
所以Sn=3n-2n.
答案:Sn=3n-2n
数列高考小题
等差数列、等比数列
关键能力·应用实践
考向一 等差、等比数列的基本量计算
【多维题组】速通关
1.已知p:数列{an}是等差数列,q:数列{an}的通项公式an=k1n+k2(k1,k2均为常数),
则p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【解析】选C.若{an}是等差数列,不妨设公差为d.
所以an=a1+(n-1)d=dn+a1-d,
令k1=d,k2=a1-d,则an=k1n+k2,
若数列{an}的通项公式an=k1n+k2(k1,k2为常数,n∈N
),
则当n≥2且n∈N
时,an-1=k1(n-1)+k2,
所以an-an-1=k1(常数)(n≥2且n∈N
),
所以{an}为等差数列,所以p是q的充要条件.
2.(2020·全国Ⅱ卷)数列
中,a1=2,am+n=aman,若ak+1+ak+2+…+ak+10=215-25,则
k=( )
A.2
B.3
C.4
D.5
【解析】选C.取m=1,则an+1=a1an,
又a1=2,所以
=2,
所以
是等比数列,则an=2n,
所以ak+1+ak+2+…+ak+10=
=2k+11-2k+1=215-25,所以k=4.
3.(2020·北京高考)在等差数列{an}中,a1=-9,a5=-1.记Tn=a1a2…an(n=1,2,…),
则数列{Tn}( )
A.有最大项,有最小项
B.有最大项,无最小项
C.无最大项,有最小项
D.无最大项,无最小项
【解析】选B.设公差为d,因为a1=-9,a5=a1+4d=-1,所以d=2,所以
a1,…,a5<0,a6,…>0,所以T1<0,T2>0,T3<0,T4>0,T5<0,以后都小于0,且越来越小.
4.(2020·全国Ⅱ卷)记Sn为等差数列{an}的前n项和.若a1=-2,a2+a6=2,则S10=________.?
【解析】设等差数列{an}的公差为d.
因为{an}是等差数列,且a1=-2,a2+a6=2,
根据等差数列通项公式:an=a1+
d,
可得a1+d+a1+5d=2,即-2+d+(-2)+5d=2,
整理可得:6d=6,解得:d=1.
根据等差数列前n项和公式:Sn=na1+
d,n∈N
,
可得:S10=10×(-2)+
=-20+45=25,
所以S10=25.
答案:25
5.已知正项数列{an}的前n项和Sn满足:Sn和2的等比中项等于an和2的等差中项,则
a1=________,Sn=________.?
【解析】由题意知
,
平方可得Sn=
,①
由a1=S1得
,
从而可解得a1=2.
又由①式得Sn-1=
(n≥2),②
①-②可得an=Sn-Sn-1=
(n≥2),
整理得(an+an-1)(an-an-1-4)=0,
因为数列{an}的各项都是正数,
所以an-an-1-4=0,即an-an-1=4.
故数列{an}是以2为首项4为公差的等差数列,
所以Sn=2n+
×4=2n2.
当n=1时,S1=a1=2.
故Sn=2n2.
答案:2 2n2
【技法点拨】提素养
等差、等比数列基本运算的关注点
(1)基本量:在等差(比)数列中,首项a1和公差d(公比q)是两个基本元素;
(2)解题思路:①设基本量a1和d(q);②列、解方程(组);把条件转化为关于a1和
d(q)的方程(组),然后求解,注意整体计算,减少计算量.
考向二 求数列的通项
【多维题组】速通关
1.(2020·临沂二模)已知数列{an}中,a1=1,an+1=
,则数列{an}的通项公式
an=________.?
【解析】因为an+1=
,a1=1,
所以an≠0,
所以
,即
.
又a1=1,则
=1,所以
是以1为首项,
为公差的等差数列.
所以
.
所以an=
(n∈N
).
答案:
2.已知数列{an}满足an+2=an+1-an,且a1=2,a2=3,则a2
021的值为________.?
【解析】由题意得,a3=a2-a1=1,a4=a3-a2=-2,a5=a4-a3=-3,a6=a5-a4=-1,a7=a6-
a5=2,a8=a7-a6=3,…,所以数列{an}是周期为6的周期数列,而2
021=6×336+5,所
以a2
021=a5=-3.
答案:-3
【变式拓展】
本题条件不变,设数列{an}的前n项和为Sn,则S2
021=________.?
【解析】由题意得,a3=a2-a1=1,a4=a3-a2=-2,a5=a4-a3=-3,a6=a5-a4=-1,a7=a6-
a5=2,a8=a7-a6=3,…,所以数列{an}是周期为6的周期数列,S6=a1+a2+a3+a4+a5+a6=0,
而2
021=6×336+5,所以S2
021=S5=1.
答案:1
3.设等比数列{an}满足a1+a3=10,a2+a4=5,则a1a2·…·an的最大值为________.
【解析】由于{an}是等比数列,设an=a1qn-1,其中a1是首项,q是公比.
所以
?
解得:
故an=
,
所以a1·a2·…·an=
=
.
当n=3或4时,
取到最小值-6,
此时
取到最大值26.
所以a1·a2·…·an的最大值为64.
答案:64
4.在数列{an}中,若a1=1,an+1=2an+3(n≥1),则该数列的通项公式an=________.?
【解析】方法一:(递推法)
an=2an-1+3=2(2an-2+3)+3=22·an-2+2×3+3
=23an-3+22×3+2×3+3=…
=2n-1·a1+2n-2·3+2n-3·3+…+3
=2n-1+3(2n-2+2n-3+…+1)=2n+1-3.
方法二:(构造法)
设an+a=2(an-1+a)(n≥2,n∈N
),
即an=2an-1+a,所以a=3.
所以an+3=2(an-1+3),
所以{an+3}是公比为2的等比数列.
所以an+3=(a1+3)·2n-1.
又a1=1,所以an=2n+1-3.
答案:2n+1-3
【技法点拨】提素养
求数列通项公式的常用方法
(1)公式法:①等差数列的通项公式;②等比数列的通项公式.
(2)已知Sn(a1+a2+…+an=Sn),求an,用作差法:
an=
(3)已知a1·a2·…·an=f(n),an≠0,求an,用作商法:
an=
(4)已知an+1-an=f(n),求an,用累加法:an=(an-an-1)+(an-1-an-2)+…+(a2-
a1)+a1=f(n-1)+f(n-2)+…+f(1)+a1(n≥2).
(5)已知
=f(n),求an,用累乘法:an=
·
·…·
·a1=f(n-1)·f(n-
2)·…·f(1)·a1(n≥2).
(6)构造等比数列法:若已知数列{an}中,an+1=pan+q(p≠0,p≠1,q≠0),a1≠
,
设存在非零常数λ,使得an+1+λ=p(an+λ),其中λ=
,则数列
就是
以a1+
为首项,p为公比的等比数列,先求出数列
的通项公式,再
求出数列{an}的通项公式即可.
(7)倒数法:若an=
(mkb≠0,n≥2),对an=
取倒数,得到
,即
.令bn=
,则{bn}可归纳为
bn+1=pbn+q(p≠0,p≠1,q≠0)型.
考向三 等差、等比数列性质综合
【多维题组】速通关
1.设等差数列{an}的前n项和为Sn,a2+a4=6,则S5等于( )
A.10
B.12
C.15
D.30
【解析】选C.由等差数列的性质可得a2+a4=a1+a5,
所以S5=
=15.
【变式拓展】
若本题再添加条件a6=9,试求该数列的前n项和Sn.
【解析】设等差数列{an}的公差为d,因为a2+a4=6,且数列为等差数列,所以a3=3,
又因为a6=9,所以公差d=2,a1=-1,其前n项和Sn=n(-1)+
×2=n2-2n.
2.(多选)设等比数列{an}的公比为q,则下列结论正确的是( )
A.数列{anan+1}是公比为q2的等比数列
B.数列{an+an+1}是公比为q的等比数列
C.数列{an-an+1}是公比为q的等比数列
D.数列
是公比为
的等比数列
【解析】选AD.对于A,由
=q2(n≥2)知数列{anan+1}是公比为q2的等比数列;
对于B,当q=-1时,数列{an+an+1}的项中有0,不是等比数列;对于C,当q=1时,数列
{an-an+1}的项中有0,不是等比数列;对于D,
,所以数列
是公比为
的等比数列.
3.(2020·全国Ⅱ卷)
北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.
上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一
环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环
依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石
板(不含天心石)( )
A.3
699块
B.3
474块
C.
3
402块
D.3
339块
【解析】选C.设每一层有n环,由题可知从内到外每环的扇面形石板数之间构成
等差数列
,且公差d=9,首项a1=9,由等差数列的性质可知Sn,S2n-Sn,S3n-S2n成等
差数列,且
=n2d,
由题意得9n2=729,所以n=9,则三层共有扇面
形石板为S3n=S27=27a1+
×9=3
402(块).
4.已知等比数列{an}的公比q>0,前n项和为Sn,若2a3,a5,3a4成等差数列,a2a4a6=64,
则q=________,Sn=________.?
【解析】由2a3,a5,3a4成等差数列得2a5=2a3+3a4?2q2=2+3q?q=2(负值舍
去),a2a4a6=64?
=64?a4=4?a1=
,Sn=
.
答案:2
【技法点拨】提素养
等差、等比数列性质问题的求解策略
(1)抓住项与项之间的关系及项与序号之间的关系,从这些特点入手选择恰当的
性质进行求解.
(2)数列是一种特殊的函数,具有函数的一些性质,如单调性、周期性等,可利用
函数的性质解题.
(3)利用数列性质进行运算时,要利用整体思想,可以减少计算量,此方法还适用
于求函数值、求函数的解析式等问题.
【加练备选】
纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采
用国际标准,规定以A0、A1、A2、B1、B2等标记来表示纸张的幅面规格.复印纸
幅面规格只采用A系列和B系列,其中系列的幅面规格为:①A0、A1、A2、…、A8
所有规格的纸张的幅宽(以x表示)和长度(以y表示)的比例关系都为x∶y=1∶
;
②将A0纸张沿长度方向对开成两等份,便成为A1规格,A1纸张沿长度方向对开成
两等份,便成为A2规格,…,如此对开至A8规格.现有A0、A1、A2、…、A8纸各一
张.若A4纸的宽度为2
dm,则A0纸的面积为________dm2;这9张纸的面积之和等于
________dm2.?
【解析】可设Ai
的纸张的长度为ai+1,面积为Si+1,Ai的幅宽为
ai+1,
A
的长度为ai+2=
ai+1,
所以,数列
是以
为公比的等比数列,
由题意知A4纸的宽度为
a5=2,所以a5=2
,
所以a1=
,所以A0纸的面积为S1=
(dm2).
又Sn=
,所以
,所以,数列
是以64
为
首项,以
为公比的等比数列,因此,这9张纸的面积之和等于
(dm2).
答案:64
题组训练·素养提升
【新题速递】
1.等比数列
的前n项和为Sn,若a1+a2+a3=3,a4+a5+a6=6,则S12=( )
A.15
B.30
C.45
D.60
【解析】选C.由题意,等比数列
的前n项和为Sn,
满足a1+a2+a3=3,a4+a5+a6=6,
则
,
所以a7+a8+a9=12,a10+a11+a12=24,
则S12=a1+a2+a3+…+a10+a11+a12=45.
2.已知等差数列
的前n项和为Sn,且a1,
,a4成公比为q的等比数列,则q等于
( )
A.1或2
B.2
C.1
D.2或4
【解析】选A.因为a1,
,a4成公比为q的等比数列,
所以
=a1·a4,
又因为
为等差数列,
设等差数列{an}的公差为d,
所以
=a1·a4,
所以
=a1·
,即
=0,
即d=0或d=a1.
所以q=
=1或q=
=2.
3.(2020·泰安二模)若等比数列{an}的各项均为正数,且a10a11+a9a12=2e5,则
ln
a1+ln
a2+…+ln
a20=________.?
【解析】因为a10a11+a9a12=2a10a11=2e5,
所以a10a11=e5.
所以ln
a1+ln
a2+…+ln
a20
=ln(a1a2…a20)
=ln[(a1a20)·(a2a19)·…·(a10a11)]
=ln(a10a11)10=10ln(a10a11)
=10ln
e5=50ln
e=50.
答案:50
4.已知数列
满足:对任意n∈N
均有an+1=pan+2p-2(p为常数,p≠0且p≠1),若
a2,a3,a4,a5∈{-18,-6,-2,6,11,30},则a1的所有可能取值的集合是________.?
【解析】因为an+1=pan+2p-2,
所以an+1+2=p(an+2),
所以①若a1=-2,则a1+1+2=p(a1+2)=0,a2=-2,同理可得,a3=a4=a5=-2,即a1=-2符合题
意;
②若a1≠-2,p为不等于0与1的常数,则数列{an+2}是以p为公比的等比数列,
因为ai∈{-18,-6,-2,6,11,30},i=2,3,4,5,
an+2可以取-16,-4,8,32,所以若|p|>1,
则p=-2,由a2+2=-4=-2(a1+2)得:a1=0;
若|p|<1,则p=-
,由a2+2=32=-
(a1+2)得:a1=-66.
综上所述,满足条件的a1的所有可能取值为-2,0,-66.
答案:
【创新迁移】
1.如图,点列{An},{Bn}分别在某锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N
,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N
(P≠Q表示
点P与Q不重合).若dn=|AnBn|,Sn为△AnBnBn+1的面积,则下列结论正确的是( )
A.{Sn}是等差数列
B.{
}是等差数列
C.{dn}是等差数列
D.{
}是等差数列
【解析】选A.由题意,过点A1,A2,A3,…,An,An+1,…分别作直线B1Bn+1的垂线,高分
别记为h1,h2,h3,…,hn,hn+1,…,根据平行线的性质,得h1,h2,h3,…,hn,hn+1,…成等
差数列,又Sn=
×|BnBn+1|×hn,|BnBn+1|为定值,所以{Sn}是等差数列.
2.已知数列{an}的前m(m≥4)项是公差为2的等差数列,从第m-1项起,
am-1,am,am+1,…成公比为2的等比数列.若a1=-2,则m=________,{an}的前6项和
S6=________.?
【解析】由a1=-2,公差d=2,
得am-1=-2+2(m-2)=2m-6,
am=-2+2(m-1)=2m-4,则
=2,
所以m=4;
所以S6=a1+a2+a3+a4+a5+a6
=-2+0+2+4+8+16=28.
答案:4 28
专题能力提升练
七 等差数列、等比数列
(40分钟 80分)
一、单项选择题(共8小题,每小题5分,共40分)
1.(2020·菏泽二模)已知等比数列{an}的公比为正数,且a3a9=2
,则公比
q=( )
A.
B.
C.
D.2
【解析】选C.a3a9=
因为q>0,所以q=
.
2.(2019·全国Ⅲ卷)已知各项均为正数的等比数列{an}的前4项的和为15,且a5=3a3+4a1,则a3=( )
A.16
B.8
C.4
D.2
【解析】选C.设该等比数列的首项为a1,公比为q,
由已知得,a1q4=3a1q2+4a1,
因为a1>0且q>0,则可解得q=2,
又因为a1(1+q+q2+q3)=15,
即可解得a1=1,则a3=a1q2=4.
3.设Sn为等差数列{an}的前n项和,若
则
=( )
【解析】选A.设公差为d,则
所以
4.已知数列{an}为等比数列,a4+a7=2,a5a6=-8,则a1+a10=( )
A.7
B.5
C.-5
D.-7
【解析】选D.设数列{an}的公比为q.由题意,得
所以
或
解得
或
当
时,a1+a10=a1(1+q9)=1+(-2)3=-7;
当
时,a1+a10=a1(1+q9)=(-8)×
=-7.
综上,a1+a10=-7.
5.已知等比数列{an}公比为q,其前n项和为Sn,若S3,S9,S6成等差数列,则q3等于
( )
A.-
B.1
C.-
或1
D.-1或
【解析】选A.若q=1,则3a1+6a1=2×9a1,
得a1=0,矛盾,故q≠1.
所以
解得q3=-
或1(舍).
6.等差数列{an}中,已知|a6|=|a11|,且公差d>0,则其前n项和取最小值时n的值为
( )
A.6
B.7
C.8
D.9
【解析】选C.由d>0可得等差数列{an}是递增数列,又|a6|=|a11|,
所以-a6=a11,即-a1-5d=a1+10d,
所以a1=-
,则a8=-
<0,a9=
>0,
所以前8项和为前n项和的最小值,故选C.
7.已知数列{an}的前n项和为Sn,且a1=2,an+1=Sn,若an∈(0,2
020),则称项an为
“和谐项”,则数列{an}的所有“和谐项”的平方和为( )
A.
×411+
B.
×411-
C.
×410+
D.
×412-
【解析】选A.因为an+1=Sn,
所以an=Sn-1(n≥2),
则an+1-an=Sn-Sn-1,
即an+1-an=an,an+1=2an,
=2,
因为a1=2,所以a2=S1=a1=2,
故an=
因为an∈(0,2
020),所以1≤n≤11,数列{an}的所有“和谐项”的平方和为
8.已知a1,a2,a3,a4依次成等比数列,且公比q不为1,将此数列删去一个数后得到的数列(按原来的顺序)是等差数列,则正数q的值是( )
【解析】选B.因为公比q不为1,所以删去的数不是a1,a4.
①若删去a2,则由2a3=a1+a4得2a1q2=a1+a1q3,又a1≠0,所以2q2=1+q3,
整理得q2(q-1)=(q-1)(q+1).
又q≠1,所以q2=q+1,
又q>0,得q=
;
②若删去a3,
则由2a2=a1+a4得2a1q=a1+a1q3,
又a1≠0,所以2q=1+q3,
整理得q(q+1)(q-1)=q-1.
又q≠1,则可得q(q+1)=1,
又q>0,得q=
.
综上所述,q=
.
二、多项选择题(共20分,全部选对得5分,选对但不全的得3分,有选错的得0分)
9.记单调递增的等比数列{an}的前n项和为Sn,若a2+a4=10,a2a3a4=64,则( )
A.Sn+1-Sn=2n+1
B.an=2n-1
C.Sn=2n-1
D.Sn=2n-1-1
【解析】选BC.由a2a3a4=64得
=43,则a3=4.
设等比数列{an}的公比为q(q≠0),
由a2+a4=10,得
+4q=10,
即2q2-5q+2=0,解得q=2或q=
.
又因为数列{an}单调递增,所以q=2,
所以2a1+8a1=10,解得a1=1.
所以an=2n-1,Sn=
=2n-1,
所以Sn+1-Sn=2n+1-1-(2n-1)=2n.
10.数列{Fn}:1,1,2,3,5,8,13,21,34,…称为斐波那契数列,是由十三世纪意大利数学家列昂纳多·斐波那契以兔子繁殖为例子而引入的,故又称为“兔子数列”.该数列从第三项开始,每项等于其前相邻两项之和.记数列{Fn}的前n项和为Sn,则下列结论正确的是( )
A.S5=F7-1
B.S5=S6-1
C.S2
019=F2
021-1
D.S2
019=F2
020-1
【解析】选AC.根据题意有Fn=Fn-1+Fn-2(n≥3),
所以S3=F1+F2+F3=1+F1+F2+F3-1=F3+F2+F3-1=F4+F3-1=F5-1,S4=F4+S3=F4+F5-1=F6-1,S5=F5+S4=F5+F6-1=F7-1,
…
所以S2
019=F2
021-1.
11.等差数列{an}是递增数列,满足a7=3a5,前n项和为Sn,下列选择项正确的是( )
A.d>0
B.a1<0
C.当n=5时Sn最小
D.Sn>0时n的最小值为8
【解析】选ABD.由题意,设等差数列{an}的公差为d,因为a7=3a5,可得
a1+6d=3(a1+4d),解得a1=-3d,又由等差数列{an}是递增数列,可知d>0,则a1<0,故
A,B正确;因为
由
可知,当n=3或4时Sn最
小,故C错误,令Sn=
n2-
n>0,解得n<0或n>7,即Sn>0时n的最小值为8,故D正确.
12.已知数列{an}是各项均为正数的等比数列,{bn}是公差不为0的等差数列,且a2=b2,a8=b8,则( )
A.a5=b5
B.a5
【解析】选BC.方法一:设{an}的公比为q(q>0),{bn}的公差为d(d≠0).
a5=
,b5=
,
由基本不等式得
≤
,
当且仅当a2=a8时等号成立.
易知数列{bn}不是常数列,故B正确,A错误.
因为a2·q6=a8=b8=b2+6d=a2+6d,
所以d=
,
所以a4-b4=a2q2-(b2+2d)=a2q2-a2-2d=a2
=
(3q2-q6-2)=
(q2-
q6+2q2-2)=
[(1-q2)(q4+q2-2)]
=-
(1-q2)2(q2+2)<0,a6-b6=a2q4-a2-4d=
(3q4-1-2q6)=-
(1-q2)2(2q2+1)<0.
故C正确,D错误.
方法二:设{an}的公比为q(q>0),{bn}的公差为d(d≠0).
an=a1qn-1=
·qn,
bn=b1+(n-1)d=b1-d+nd,
将其分别理解成关于n的类指数函数(指数函数的图象为下凹曲线)和一次函数
(一次函数的图象为直线),则两函数图象在n=2,n=8处相交,故an
若正项数列{an}满足an+1=an-ln
an,0
,则下列说法正确的是( )
A.对任意的n∈N
,恒有an+1≥1
B.对任意的n∈N
,恒有Sn>n
C.对任意的n∈N
,恒有0
,恒有Sn≥Tn
【解析】选ACD.设函数f(x)=x-ln
x(x>0),则f′(x)=1-
=
,
所以函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,故f(x)min=f(1)=1.
又an+1=an-ln
an,所以an+1≥1,A正确;
因为0
an,所以an-an+1=ln
an,
所以a1-an+1=(a1-a2)+(a2-a3)+…+(an-an+1)
=ln
a1+ln
a2+…+ln
an
=ln(a1·a2·…·an)<0,
故a1·a2·…·an<1,即0
三、填空题(共4小题,每小题5分,共20分)
13.(2020·全国Ⅰ卷)数列{an}满足an+2+(-1)nan=3n-1,前16项和为540,则
a1=________.?
【解析】an+2+(-1)nan=3n-1,
当n为奇数时,an+2=an+3n-1;
当n为偶数时,an+2+an=3n-1.
设数列
的前n项和为Sn,
S16=a1+a2+a3+a4+…+a16
=a1+a3+a5+…+a15+(a2+a4)+…+(a14+a16)
=a1+(a1+2)+(a1+10)+(a1+24)+(a1+44)+(a1+70)
+(a1+102)+(a1+140)+(5+17+29+41)
=8a1+392+92=8a1+484=540,
所以a1=7.
答案:7
【加练备选】
设{an}是公差不为零的等差数列,Sn为其前n项和,已知S1,S2,S4成等比数列,且a3=5,则数列{an}的通项公式为________.?
【解析】设数列{an}的公差为d(d≠0),因为{an}是等差数列,S1,S2,S4成等比数列,所以(a1+a2)2=a1(a1+a2+a3+a4),因为a3=5,所以(5-2d+5-d)2=(5-2d)(5-2d+15),解得d=2或d=0(舍去),所以5=a1+(3-1)×2,即a1=1,所以an=2n-1.
答案:an=2n-1
14.设等比数列{an}的前n项和为Sn,满足对任意的正整数n,均有Sn+3=8Sn+3,则
a1=________,公比q=________.?
【解析】由Sn+3=8Sn+3,则Sn+2=8Sn-1+3,
两式相减得,an+3=8an?anq3=8an,
则q3=8?q=2,
由等比数列前n项和公式得,
即2n+3a1-a1=8·2na1-8a1+3,
从而解得a1=
.
答案:
2
【加练备选】
已知数列{an}的前n项和Sn=n2+2n-1(n∈N
),则a1=________;数列{an}的通项公式
为an=________.?
【解析】因为Sn=n2+2n-1,
当n=1时,a1=1+2-1=2,
当n≥2时,an=Sn-Sn-1=n2+2n-1-[(n-1)2+2(n-1)-1]=2n+1,a1=2不满足an=2n+1,所
以an=
答案:2
15.已知数列{an}的通项公式an=-n2+10n-21,前n项和为Sn,若n>m,则Sn-Sm的最大值是________.?
【解析】数列{an}的通项公式an=-n2+10n-21=-(n-3)(n-7),当3≤n≤7时,an≥0,当n≤2或n≥8时,an<0,Sn最大值为S6或S7,Sm最小值为S2或S3,Sn-Sm的最大值为S6-S3=a4+a5+a6=3+4+3=10.
答案:10
16.已知数列{an}满足a1=
,an=
(n≥2,n∈N
),则通项公式
an=________.?
【解析】由
令
=bn,则bn=
·bn-1+
?bn-
1=
·(bn-1-1),由a1=
,得b1-1=-
,所以{bn-1}是以-
为首项,
为公比
的等比数列,所以bn-1=
得
答案:
【加练备选】
数列{an}中,前n项和为Sn,a1=1,an+1=Sn+3n(n∈N
,n≥1),则数列{Sn}的通项公式为
________.?
【解析】因为an+1=Sn+3n=Sn+1-Sn,所以Sn+1=2Sn+3n,所以
所以
又
所以数列
是首项为-
,公比为
的等比数列,
所以
所以Sn=3n-2n.
答案:Sn=3n-2n
同课章节目录
