数列解答题数列求和及数列的综合应用课件2021高考数学二轮(共PPT104张)
文档属性
| 名称 | 数列解答题数列求和及数列的综合应用课件2021高考数学二轮(共PPT104张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 22:15:57 | ||
图片预览











文档简介
(共104张PPT)
数列解答题
数列求和及数列的综合应用
考向一 等差(等比)数列的判断与证明(规范解答)
【典例】(2019·全国Ⅱ卷)已知数列{an}和{bn}满足a1=1,b1=0,4an+1=3an-
bn+4,4bn+1=3bn-an-4.
(1)证明:{an+bn}是等比数列,{an-bn}是等差数列;
(2)求{an}和{bn}的通项公式.
【思维流程图】
(1)由已知两个递推公式→求和(差)得出相应的关系式→再依据定义即可得出结论.
(2)求出{an+bn}与{an-bn}的通项公式→利用方程思想即可得出结论.
【规范解答】(1)由题设得4(an+1+bn+1)=2(an+bn),
即an+1+bn+1=
(an+bn).
…………………………………………………………2分
又因为a1+b1=1,所以
是首项为1,公比为
的等比数列.
……………3分
由题设得4(an+1-bn+1)=4(an-bn)+8,即an+1-bn+1=an-bn+2.
又因为a1-b1=1,所以
是首项为1,公差为2的等差数列.………………
6分
考查要求
基础性
学科素养
逻辑推理、数学运算
评分细则
已知两式相加、相减各得2分;由代数式
得出等差、等比数列各得1分
(2)由(1)知,an+bn=
,an-bn=2n-1.
……………………………
8分
所以an=
[(an+bn)+(an-bn)]=
+n-
,
………………………10分
bn=
[(an+bn)-(an-bn)]=
-n+
.
……………………………12分
考查要求
综合性
学科素养
逻辑推理、数学运算
评分细则
求出{an+bn}与{an―bn}的通项公式得2分,
分别求出数列{an}与{bn}的通项公式各得2分
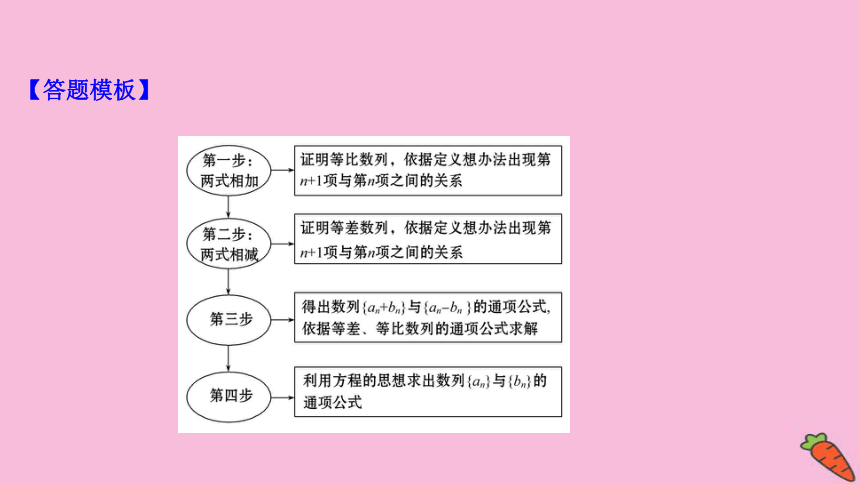
【答题模板】
【素养提升】
1.证明数列{an}是等差数列的两种基本方法
(1)利用定义,证明an+1-an(n∈N
)为一常数;
(2)利用等差中项,即证明2an=an-1+an+1(n≥2).
2.证明数列{an}是等比数列的两种基本方法
(1)利用定义,证明
(n∈N
)为一常数;
(2)利用等比中项,即证明
=an-1an+1(n≥2).
3.若要判断一个数列不是等差(等比)数列,只需判断存在连续三项不成等差(等
比)数列即可.
【变式训练】
1.已知数列{an}满足a1=1,nan+1=2(n+1)an.设bn=
.
(1)求b1,b2,b3;
(2)判断数列{bn}是否为等比数列,并说明理由;
(3)求{an}的通项公式.
【解析】(1)由条件可得an+1=
an.
将n=1代入得,a2=4a1,而a1=1,所以,a2=4.
将n=2代入得,a3=3a2,所以a3=12.
从而b1=1,b2=2,b3=4.
(2){bn}是首项为1,公比为2的等比数列.
由条件可得
,即bn+1=2bn,
又b1=1,所以{bn}是首项为1,公比为2的等比数列.
(3)由(2)可得
=2n-1,所以an=n·2n-1.
【加练备选】
成等差数列的三个正数的和等于15,并且这三个数分别加上2,5,13后成为
等比数列{bn}中的b3,b4,b5.
(1)求数列{bn}的通项公式;
(2)数列{bn}的前n项和为Sn,求证:数列
是等比数列.
【解析】(1)设成等差数列的三个正数分别为a-d,a,a+d.
依题意,得a-d+a+a+d=15.
解得a=5.
所以{bn}中的b3,b4,b5依次为7-d,10,18+d.
依题意,有(7-d)(18+d)=100,
解得d=2或d=-13(舍去).
故{bn}的第3项为5,公比为2.
由b3=b1·22,即5=b1·22,解得b1=
.
所以bn=b1·qn-1=
·2n-1=5·2n-3,
即数列{bn}的通项公式bn=5·2n-3.
(2)数列{bn}的前n项和Sn=
=5·2n-2-
,即Sn+
=5·2n-2.
由S1+
=2可知,
数列
是以
为首项,2为公比的等比数列.
2.设Sn为数列{an}的前n项和,对任意的n∈N
,都有Sn=2-an,数列{bn}满足
b1=2a1,bn=
(n≥2,n∈N
).
(1)求证:数列{an}是等比数列,并求{an}的通项公式;
(2)判断数列
是等差数列还是等比数列,并求数列{bn}的通项公式.
【解析】(1)当n=1时,a1=S1=2-a1,解得a1=1;
当n≥2时,an=Sn-Sn-1=an-1-an,
即
(n≥2,n∈N
).
所以数列{an}是首项为1,公比为
的等比数列,
故数列{an}的通项公式为an=
.
(2)因为a1=1,所以b1=2a1=2.
因为bn=
,
所以
,
即
(n≥2).
所以数列
是首项为
,
公差为1的等差数列.
所以
,
故数列{bn}的通项公式为bn=
.
【加练备选】
已知数列{an}满足an+1-3an=3n(n∈N
)且a1=1.设bn=
,
(1)证明数列{bn}为等差数列;
(2)设cn=
,求数列{cn}的前n项和Sn.
【解析】(1)由已知得an+1=3an+3n,得bn+1=
=bn+1,所以
bn+1-bn=1,又a1=1,所以b1=1,
所以数列{bn}是首项为1,公差为1的等差数列.
(2)bn=
=n,所以an=n·3n-1,cn=
,
所以Sn=
.
考向二 等差(等比)数列的求和
命题角度1 等差数列的通项与求和
【典例】(2020·全国Ⅲ卷)设等比数列{an}满足a1+a2=4,a3-a1=8.
(1)求{an}的通项公式;
(2)记Sn为数列{log3an}的前n项和.若Sm+Sm+1=Sm+3,求m.
【解析】(1)设等比数列{an}的公比为q,
根据题意,有
,解得
,所以an=3n-1.
(2)令bn=log3an=log33n-1=n-1,
所以Sn=
,
根据Sm+Sm+1=Sm+3,
可得
,
整理得m2-5m-6=0,因为m>0,所以m=6.
【探究延伸】
若本题的条件不变,试求数列{log3an-9}的前n项和的最小值.
【解析】依典例知an=3n-1,所以log3an-9=log33n-1-9=n-10,设其前n项和为Tn,则
Tn=
,又n∈N
,所以当n=9或10时,Tn最小,
其最小值=
=-45.
命题角度2 等比数列的通项与求和
【典例】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明
是等比数列,并求{an}的通项公式;
(2)证明:
+…+
.
【解析】(1)由an+1=3an+1得
.
又a1+
,
所以
是首项为
,公比为3的等比数列.
an+
,
因此{an}的通项公式为an=
.
(2)由(1)知
.
因为当n≥1时,3n-1≥2×3n-1,
所以
.
于是
+…+
≤1+
+…+
=
.
所以
+…+
.
【素养提升】
等差(等比)数列求和的几点注意
一是注意弄清项数;二是注意公式的适用条件;三是注意运算的准确性.
【变式训练】
1.已知数列{an}是等比数列,公比q<1,若a2=2,a1+a2+a3=7.
(1)求{an}的通项公式;
(2)设bn=log2an,求数列{bn}的前n项和.
【解析】(1)由已知得
则
或
(舍去).
所以an=4×
=23-n.
(2)因为bn=log2an=log223-n=3-n,
所以数列{bn}是首项为2,公差为-1的等差数列.
设数列{bn}的前n项和为Tn,
则Tn=
.
2.已知等差数列{an}前三项的和为-9,前三项的积为-15.
(1)求等差数列{an}的通项公式;
(2)若{an}为递增数列,求数列{|an|}的前n项和Sn.
【解析】(1)设等差数列{an}的公差为d,
则依题意得a2=-3,则a1=-3-d,a3=-3+d,
所以(-3-d)(-3)(-3+d)=-15,得d2=4,d=±2,
所以an=-2n+1或an=2n-7.
(2)由题意得an=2n-7,所以|an|=
①n≤3时,Sn=-(a1+a2+…+an)=
n
=6n-n2;
②n≥4时,Sn=-a1-a2-a3+a4+…+an=-2(a1+a2+a3)+(a1+a2+…+an)=18-6n+n2.
综上,数列{|an|}的前n项和Sn=
考向三 数列求和
命题角度1 错位相减法求和
【典例】(2020·全国Ⅰ卷)设{an}是公比不为1的等比数列,a1为a2,a3的等差中项.
(1)求{an}的公比;
(2)若a1=1,求数列{nan}的前n项和.
【解析】(1)设{an}的公比为q,
由题设得2a1=a2+a3,即2a1=a1q+a1q2.
因为a1≠0,
所以q2+q-2=0,
解得q=1(舍去),q=-2.
故{an}的公比为-2.
(2)设Sn为{nan}的前n项和.
由(1)及题设可得,an=(-2)n-1.
所以Sn=1+2×(-2)+…+n×(-2)n-1,
-2Sn=-2+2×(-2)2+…+(n-1)×(-2)n-1+n×(-2)n.
可得3Sn=1+(-2)+(-2)2+…+(-2)n-1-n×(-2)n=
-n×(-2)n.
所以Sn=
.
【探究延伸】
若例(2)中a1=1改为a1=2,结果如何?
【解析】设{nan}的前n项和为Sn,a1=2,
an=2·(-2)n-1=-(-2)n,
Sn=-[1×(-2)1+2×(-2)2+3×(-2)3+…+n(-2)n],
即-Sn=1×(-2)1+2×(-2)2+3×(-2)3+…+n(-2)n①,
2Sn=1×(-2)2+2×(-2)3+3×(-2)4+…+n(-2)n+1②,
①-②得:-3Sn=(-2)1+(-2)2+(-2)3+…+(-2)n-n·(-2)n+1
=
-n·(-2)n+1
=-
[1-(-2)n]-n·(-2)n+1,
所以Sn=
[1-(-2)n]+
(-2)n+1
=
-
(-2)n-
(-2)n
=
-
·(-2)n.
命题角度2 裂项相消法求和
【典例】在①a3+a5=5,S4=7;②4Sn=n2+3n;③5S4=14S2,a5是a3与
的等比中项,这
三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
已知Sn为等差数列{an}的前n项和,若________.?
(1)求an;
(2)记bn=
,求数列{bn}的前n项和Tn.
【解析】(1)选择条件①:设等差数列{an}的公差为d,
则
,解得
,
故an=
;
选择条件②:4Sn=n2+3n,
当n≥2时,4an=4Sn-4Sn-1=n2+3n-[(n-1)2+3(n-1)]=2n+2,即an=
(n≥2),
当n=1时,a1=S1=
=1,也适合上式,
故an=
;
选择条件③:设等差数列{an}的公差为d,
则
,
解得a1=1,d=
或a1=0,d=0(不合题意),
故an=
.
(2)因为an=
,所以bn=
=
,
故Tn=b1+b2+…+bn=2
+…+
.
【加练备选】
已知Sn为各项均为正数的数列{an}的前n项和,a1∈(0,2),
+3an+2=6Sn.
(1)求{an}的通项公式;
(2)设bn=
,数列{bn}的前n项和为Tn,若对任意的n∈N
,t≤4Tn恒成立,求实数
t的最大值.
【解析】(1)当n=1时,由
+3an+2=6Sn,得
+3a1+2=6a1,即
-3a1+2=0.
又a1∈(0,2),解得a1=1.
由
+3an+2=6Sn,可知
+3an+1+2=6Sn+1.
两式相减,得
-
+3(an+1-an)=6an+1,
即(an+1+an)(an+1-an-3)=0.
由于an>0,可得an+1-an-3=0,即an+1-an=3,
所以{an}是首项为1,公差为3的等差数列,
所以an=1+3(n-1)=3n-2.
(2)bn=
=
,
Tn=b1+b2+…+bn
=
=
.
因为Tn=
,随着n的增大而增大,所以数列{Tn}是递增数列,
所以t≤4Tn?
≤Tn?
≤T1=
?t≤1,所以实数t的最大值是1.
命题角度3 分组或并项求和
【典例】若数列{bn}对于n∈N
,都有bn+2-bn=d(常数),则称数列{bn}是公差为d的
准等差数列,如数列{cn},若cn=
则数列{cn}是公差为8的准等差
数列.设数列{an}满足a1=a,对于n∈N
,都有an+an+1=2n.
(1)求证:{an}为准等差数列;
(2)求{an}的通项公式及前20项和S20.
【解析】(1)因为an+1+an=2n,①
所以an+2+an+1=2n+2.②
由②-①得an+2-an=2(n∈N
),
所以{an}是公差为2的准等差数列.
(2)已知a1=a,an+1+an=2n(n∈N
),
所以a1+a2=2,即a2=2-a.
所以由(1)可知a1,a3,a5,…成以a为首项,2为公差的等差数列,a2,a4,a6,…成以
2-a为首项,2为公差的等差数列.
所以当n为偶数时,an=2-a+
×2=n-a,
当n为奇数时,an=a+
×2=n+a-1,
所以an=
S20=a1+a2+…+a19+a20
=(a1+a2)+(a3+a4)+…+(a19+a20)
=2×1+2×3+…+2×19=2×
=200.
【探究延伸】
题设中的条件不变,求S2n.
【解析】由典例解析可知:
S2n=(a1+a2)+(a3+a4)+(a5+a6)+…+(a2n-1+a2n)
=2×1+2×3+2×5+…+2×(2n-1)
=2×
=2n2.
【素养提升】
1.用错位相减法求和时应注意的两点
(1)要善于识别题目类型,特别是等比数列公比为负数的数列;
(2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”,以便下
一步准确写出“Sn-qSn”的表达式.
2.利用裂项相消法求和的注意事项
(1)抵消后并不一定只剩下第一项和最后一项,也有可能前面剩两项,后面也剩两
项;或者前面剩几项,后面也剩几项;
(2)裂项相消求和法是数列求和的重要方法之一,其基本形式为:若{an}是等差数
列且an≠0,则
.
3.并项求和法
一个数列的前n项和可两两结合求解,则称为并项求和.形如an=(-1)nf(n)类型,可
采用并项求和法求解.
【变式训练】
1.(2020·济宁二模)已知数列{an}是单调递增的等差数列,a1=1,且a1+2,2a2,a3+7
成等比数列.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,数列{bn}满足
=(-1)nan+1,求数列{bn}的
前n项和Tn.
【解析】(1)由题意,设{an}的公差为d,且d>0,
因为a1=1,且a1+2,2a2,a3+7成等比数列,
所以22
=(a1+2)×(a3+7),
即22(d+1)2=3×(1+2d+7),
解得d=2,d=-
(舍).
所以an=a1+2×(n-1)=2n-1.
(2)因为an=2n-1,
所以Sn=
=n2,Sn+1=(n+1)2,
所以
=n(n+1),
因为bn
=(-1)nan+1,an+1=2n+1,
所以bn=(-1)n
=(-1)n
.
当n为偶数时,Tn=-
-…
+
,
当n为奇数时,Tn=-
-…
-
.
所以当n为偶数时,Tn=-1+
;
当n为奇数时,Tn=-1-
.
2.(2019·天津高考)设{an}是等差数列,{bn}是等比数列,公比大于0,已知
a1=b1=3,b2=a3,b3=4a2+3.
(1)求{an}和{bn}的通项公式;
(2)设数列{cn}满足cn=
求a1c1+a2c2+…+a2nc2n(n∈N
).
【解析】(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,依题意,得
解得
故an=3+3(n-1)=3n,bn=3×3n-1=3n.
所以,{an}的通项公式为an=3n,{bn}的通项公式为bn=3n.
(2)a1c1+a2c2+…+a2nc2n
=(a1+a3+a5+…+a2n-1)+(a2b1+a4b2+a6b3+…+a2nbn)
=
+(6×31+12×32+18×33+…+6n×3n)
=3n2+6×(1×31+2×32+…+n×3n).
记Tn=1×31+2×32+…+n×3n, ①
则3Tn=1×32+2×33+…+n×3n+1,②
②-①得,2Tn=-3-32-33-…-3n+n×3n+1=-
+n×3n+1=
.
所以a1c1+a2c2+…+a2nc2n=3n2+6Tn=3n2+3×
=
(n∈N
).
考向四 数列的综合问题
命题角度1 数列与概率交汇问题
【典例】棋盘上标有第0,1,2,…,100站,棋子开始时位于第0站,棋手抛掷均匀硬
币走跳棋游戏.若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,
直到跳到第99站(胜利大本营)或第100站(失败集中营)时游戏结束.设棋子跳到
第n站的概率为Pn.
(1)求P3的值;
(2)证明:Pn+1-Pn=-
(Pn-Pn-1)(2≤n≤98).
【解析】(1)棋子跳到第3站有以下三种途径:连续三次掷出正面,其概率为
;
第一次掷出反面,第二次掷出正面,其概率为
;
第一次掷出正面,第二次掷出反面,其概率为
,因此P3=
.
(2)(用构造法证明)易知棋子先跳到第n-2站,再掷出反面,其概率为
Pn-2;
棋子先跳到第n-1站,再掷出正面,其概率为
Pn-1,因此有Pn=
(Pn-1+Pn-2),
即Pn-Pn-1=-
(Pn-1-Pn-2),
也即Pn+1-Pn=-
(Pn-Pn-1)(2≤n≤98).
命题角度2 数列与函数、不等式的交汇问题
【典例】若数列{an}的前n项和为Sn,点(an,Sn)在y=
-
x的图象上(x∈N
).
(1)求数列{an}的通项公式;
(2)若c1=0,且对任意正整数n都有cn+1-cn=
an,求证:对任意正整数n≥2,总
有
.
【解析】(1)因为Sn=
-
an,
所以当n≥2时,an=Sn-Sn-1=
an-1-
an,
所以an=
an-1,
又因为S1=
-
a1,所以a1=
,
所以an=
.
(2)由cn+1-cn=
=2n+1,得当n≥2时,
cn=c1+(c2-c1)+(c3-c2)+…+(cn-cn-1)=0+3+5+…+(2n-1)=n2-1=(n+1)(n-1).
所以
=
=
.
又因为
,所以原式得证.
【素养提升】
1.解决数列与函数综合问题的注意点
(1)数列是一类特殊的函数,其定义域是正整数集,而不是某个区间上的连续实数,
所以它的图象是一群孤立的点.
(2)转化以函数为背景的条件时,应注意题中的限制条件,如函数的定义域,这往
往是非常容易忽视的问题.
(3)利用函数的方法研究数列中相关问题时,应准确构造函数,注意数列中相关限
制条件的转化.
2.数列中不等式问题的处理方法
(1)函数法:即构造函数,通过函数的单调性、极值等得出关于正实数的不等式,
通过对关于正实数的不等式特殊赋值得出数列中的不等式.
(2)放缩法:数列中不等式可以通过对中间过程或最后的结果放缩得到.
(3)比较法:作差或者作商比较法.
【变式训练】
已知函数f(x)的图象过定点(1,1),且对任意的实数x1,x2∈R,都有
f(x1+x2)=1+f(x1)+f(x2).
(1)证明数列
(n∈N
)为等比数列;
(2)若bn=
,数列{bn}的前n项和为Tn,不等式T2n-Tn>
log2(x+1)(n≥2,n∈N
)
恒成立,求实数x的取值范围.
【解析】(1)令x1=x2=
,则
,
即f
=1+2f
,
则f
+1=2
,
令x1=x2=
,因为函数f(x)的图象过定点(1,1),所以f(1)=1+2f
=1,得f
=0,所以数列
是等比数列,公比为
,首项为1.
(2)由题意知函数f(x)的图象过定点(1,1),
所以f(1)=1.
令x1=n,x2=1,
则f(n+1)=1+f(1)+f(n),
即f(n+1)=f(n)+2,
则{f(n)}是等差数列,公差为2,首项为1,
故f(n)=1+(n-1)·2=2n-1.
因为bn=
,所以bn=
=
.
设g(n)=T2n-Tn=bn+1+bn+2+…+b2n=
,
则g(n+1)-g(n)=
=
>0,
所以{g(n)}是递增数列,g(n)min=g(2)=
+
=
,
从而
log2(x+1)<
,即log2(x+1)<2,则
解得x∈(-1,3),
所以实数x的取值范围为(-1,3).
专题能力提升练
八 数列求和及数列的综合应用
(40分钟 80分)
1.已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1=-1,
b1=1,a2+b2=3.
(1)若a3+b3=7,求{bn}的通项公式;
(2)若T3=13,求Sn.
【解析】(1)设数列{an}的公差为d,数列{bn}的公比为q,
则an=-1+(n-1)d,bn=qn-1.
由a2+b2=3,得d+q=4,(
)
由a3+b3=7,得2d+q2=8,(
)
联立(
)(
),解得q=2或q=0(舍去),
因此数列{bn}的通项公式为bn=2n-1.
(2)因为T3=1+q+q2,所以1+q+q2=13,
解得q=3或q=-4,
由a2+b2=3,得d=4-q,所以d=1或d=8.
由Sn=na1+
n(n-1)d,
得Sn=
n2-
n或Sn=4n2-5n.
2.设Sn为数列{an}的前n项和,已知a3=7,an=2an-1+a2-2(n≥2).
(1)证明:数列{an+1}为等比数列;
(2)求数列{an}的通项公式,并判断n,an,Sn是否成等差数列.
【解析】(1)因为a3=7,a3=3a2-2,所以a2=3,
所以an=2an-1+1,
所以a1=1,
=2(n≥2),
所以数列{an+1}是首项为a1+1=2,公比为2的等比数列.
(2)由(1)知,an+1=2n,所以an=2n-1,
所以Sn=
-n=2n+1-n-2,所以n+Sn-2an=n+(2n+1-n-2)-2(2n-1)=0,
所以n+Sn=2an,
即n,an,Sn成等差数列.
【加练备选】
设数列{an}的前n项和为Sn,n∈N
.已知a1=1,a2=
,a3=
,且当n≥2时,
4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明:{an+1-
an}为等比数列;
(3)求数列{an}的通项公式.
【解析】(1)当n=2时,4S4+5S2=8S3+S1,
即
解得:a4=
.
(2)因为4Sn+2+5Sn=8Sn+1+Sn-1(n≥2),
所以4Sn+2-4Sn+1+Sn-Sn-1=4Sn+1-4Sn(n≥2),即4an+2+an=4an+1(n≥2),
因为4a3+a1=4×
+1=6=4a2,
所以4an+2+an=4an+1,
因为
所以数列
是以a2-
a1=1为首项,公比为
的等比数列.
(3)由(2)知,
是以1为首项,公比为
的等比数列,
所以an+1-
an=
.
即
所以
是以
=2为首项,4为公差的等差数列,
所以
=2+(n-1)×4=4n-2,即an=(4n-2)×
=(2n-1)×
.
所以数列{an}的通项公式是an=(2n-1)×
.
3.(2020·临沂二模)已知数列{an}满足a1=2,(n+2)an=(n+1)an+1-2(n2+3n+2),设
bn=
.
(1)证明数列{bn}是等差数列;
(2)设
=2n+1,求数列{cn}的前n项和Tn(n∈N
).
【解析】(1)因为a1=2,所以b1=
=1.
将(n+2)an=(n+1)an+1-2(n2+3n+2)两边同时除以(n+1)(n+2)得:
所以
=2,即bn+1-bn=2.
所以数列{bn}是以1为首项,2为公差的等差数列.
(2)由(1)得bn=1+2(n-1)=2n-1.
因为
=2n+1,
所以cn=(2n+1)bn=(2n-1)·2n+2n-1.
设Pn=1×2+3×22+5×23+…+(2n-1)·2n,
2Pn=1×22+3×23+…+(2n-3)·2n+(2n-1)·2n+1,
两式相减得:-Pn=2+2(22+23+…+2n)-(2n-1)·2n+1
化简得Pn=6+(2n-3)·2n+1.
设Sn=1+3+5+…+(2n-1)=
=n2,所以Tn=Pn+Sn=6+(2n-3)·2n+1+n2.
4.已知等差数列{an}的前n项和为Sn,{bn}是各项均为正数的等比数列,a1=b4,________,b2=8,b1-3b3=4,是否存在正整数k,使得数列
的前k项和
Tk>
?若存在,求出k的最小值;若不存在,说明理由.?
从①S4=20,②S3=2a3,③3a3-a4=b2这三个条件中任选一个,补充到上面问题中并作
答.
(注:如果选择多个条件分别解答,按第一个解答计分.)
【解析】设等比数列{bn}的公比为q(q>0),则b1=
,b3=8q,于是
-3×8q=4,即
6q2+q-2=0,
解得q=
,q=-
(舍去).
若选①:则a1=b4=2,S4=4a1+
d=20,解得d=2,
所以
令1-
>
,解得k>15,
因为k为正整数,所以k的最小值为16.
若选②:则a1=b4=2,3a1+
d=2(a1+2d),解得d=2.
下同①.
若选③:则a1=b4=2,3(a1+2d)-(a1+3d)=8,解得d=
.
于是
于是
令Tk>
,得
<
,
注意到k为正整数,解得k≥7,所以k的最小值为7.
5.(2020·新高考全国Ⅰ卷)已知公比大于1的等比数列{an}满足a2+a4=20,a3=8.
(1)求{an}的通项公式;
(2)记bm为{an}在区间(0,m](m∈N
)中的项的个数,求数列{bm}的前100项和S100.
【命题意图】本题考查等比数列通项公式的应用,考查数列基本量的运算求解能力.体现了数学运算与数学抽象的核心素养.
【解析】(1)设{an}的公比为q.
由题设得a1q+a1q3=20,a1q2=8.
解得q=
(舍去),或q=2,a1=2.
所以{an}的通项公式为an=2n.
(2)由题设及(1)知b1=0,且当2n≤m<2n+1时,bm=n.
所以
S100=b1+(b2+b3)+(b4+b5+b6+b7)+…+(b32+b33+…+b63)+(b64+b65+…+b100)=0+1×2+2×22
+3×23+4×24+5×25+6×(100-63)=480.
6.已知数列{an}满足an=3an-1+k3n-1(n∈N
,n≥2,k∈R).
(1)设a1=1,k=0,证明数列{an-
}是等比数列;
(2)对任意k∈R,是否存在一个实数t,使得bn=
(an+t)(n∈N
)且{bn}为等差数列?
若存在,求出t的值;若不存在,请说明理由.
【解析】(1)当k=0时,an=3an-1-1,
所以
又a1-
=
≠0,所以数列
是首项为
,公比为3的等比数列.
(2)当n≥2时,bn-bn-1
=
(an+t)-
(an-1+t)
=
(an+t-3an-1-3t)
=
(3an-1+k3n-1+t-3an-1-3t)
=
(k3n-1-2t)=k-
.
要使{bn}为等差数列,则必须使1+2t=0,
所以t=-
,
即对任意的k∈R,存在t=-
,使{bn}为等差数列.
【加练备选】
已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.
(1)求数列{xn}的通项公式;
(2)如图,在平面直角坐标系xOy中,依次连接点P1(x1,1),P2(x2,2),…,Pn+1(xn+1,n+1)得到折线P1
P2…Pn+1,求由该折线与直线y=0,x=x1,x=xn+1所围成的区域的面积Tn.
【解析】(1)设数列{xn}的公比为q,
由题意得
所以3q2-5q-2=0.
因为q>0,
所以q=2,x1=1,
因此数列{xn}的通项公式为xn=2n-1.
(2)过P1,P2,…,Pn+1向x轴作垂线,垂足分别为Q1,Q2,…,Qn+1.
由(1)得xn+1-xn=2n-2n-1=2n-1,
记梯形PnPn+1Qn+1Qn的面积为bn,
由题意得bn=
×2n-1=(2n+1)×2n-2,
所以Tn=b1+b2+…+bn
=3×2-1+5×20+7×21+…+(2n-1)×2n-3+(2n+1)×2n-2.(i)
又2Tn=3×20+5×21+7×22+…+(2n-1)×2n-2+(2n+1)×2n-1.(ii)
(i)-(ii)得-Tn=3×2-1+(2+22+…+2n-1)-(2n+1)×2n-1=
-(2n+1)×2n-1.
所以Tn=
.
7.已知等比数列{an}的公比q>1,a1=2,且a1,a2,a3-8成等差数列,数列{anbn}的前n
项和为
.
(1)分别求出数列{an}和{bn}的通项公式;
(2)设数列
的前n项和为Sn,已知?n∈N
,Sn≤m恒成立,求实数m的最小值.
【解析】(1)因为a1=2,且a1,a2,a3-8成等差数列,
所以2a2=a1+a3-8,
即2a1q=a1+a1q2-8,
所以q2-2q-3=0,
所以q=3或-1,而q>1,
所以q=3,
所以an=2·3n-1.
因为a1b1+a2b2+…+anbn=
,
所以a1b1+a2b2+…+an-1bn-1
=
,
两式相减得anbn=2n·3n-1(n≥2).
因为an=2·3n-1,所以bn=n(n≥2),
令n=1,可得b1=1,所以bn=n.
(2)因为数列{an}是首项为2,公比为3的等比数列,
所以数列
是首项为
,公比为
的等比数列,
所以
因为?n∈N
,Sn≤m恒成立,
故实数m的最小值为
.
【加练备选】
已知数列{an}满足a1=
,an+1an=2an+1-1(n∈N
),令bn=an-1.
(1)求数列{bn}的通项公式;
(2)令cn=
,求证:c1+c2+…+cn.
【解析】(1)因为an+1an=2an+1-1(n∈N
),bn=an-1,即an=bn+1.
所以(bn+1+1)(bn+1)=2(bn+1+1)-1,
化为:
因为a1=
,所以b1=a1-1=-
,
所以
=-2,所以数列
是等差数列,首项为-2,公差为-1.
所以
=-2-(n-1)=-1-n,
所以bn=-
.
(2)由(1)可得:an=bn+1=1-
.
所以
因为n≥2时,2n+2≤2n+1-1,
所以
所以c1+c2+…+cn<
8.设函数fn(x)=x-(3n-1)x2(其中n∈N
),区间In={x|fn(x)>0}.
(1)定义区间(α,β)的长度为β-α,求区间In的长度;
(2)把区间In的长度记作数列{an},
令bn=an·an+1,
①求数列{bn}的前n项和Tn;
②是否存在正整数m,n(1【解析】(1)由fn(x)>0,得x-(3n-1)x2>0,
解得0,即In=
.
所以区间的长度为
-0=
.
(2)由(1)知an=
.
①因为bn=an·an+1=
,
所以Tn=b1+b2+…+bn
②由①知T1=
,Tm=
,
Tn=
.
假设存在正整数m,n(1=T1Tn,
化简得
所以(-3m2+6m+2)n=5m2.(
)
当m=2时,(
)式可化为2n=20,所以n=10.
当m≥3时,-3m2+6m+2=-3(m-1)2+5≤-7<0.
又因为5m2>0,所以(
)式可化为
n=
<0,此时n无正整数解.
综上,存在正整数m=2,n=10满足条件.
数列解答题
数列求和及数列的综合应用
考向一 等差(等比)数列的判断与证明(规范解答)
【典例】(2019·全国Ⅱ卷)已知数列{an}和{bn}满足a1=1,b1=0,4an+1=3an-
bn+4,4bn+1=3bn-an-4.
(1)证明:{an+bn}是等比数列,{an-bn}是等差数列;
(2)求{an}和{bn}的通项公式.
【思维流程图】
(1)由已知两个递推公式→求和(差)得出相应的关系式→再依据定义即可得出结论.
(2)求出{an+bn}与{an-bn}的通项公式→利用方程思想即可得出结论.
【规范解答】(1)由题设得4(an+1+bn+1)=2(an+bn),
即an+1+bn+1=
(an+bn).
…………………………………………………………2分
又因为a1+b1=1,所以
是首项为1,公比为
的等比数列.
……………3分
由题设得4(an+1-bn+1)=4(an-bn)+8,即an+1-bn+1=an-bn+2.
又因为a1-b1=1,所以
是首项为1,公差为2的等差数列.………………
6分
考查要求
基础性
学科素养
逻辑推理、数学运算
评分细则
已知两式相加、相减各得2分;由代数式
得出等差、等比数列各得1分
(2)由(1)知,an+bn=
,an-bn=2n-1.
……………………………
8分
所以an=
[(an+bn)+(an-bn)]=
+n-
,
………………………10分
bn=
[(an+bn)-(an-bn)]=
-n+
.
……………………………12分
考查要求
综合性
学科素养
逻辑推理、数学运算
评分细则
求出{an+bn}与{an―bn}的通项公式得2分,
分别求出数列{an}与{bn}的通项公式各得2分
【答题模板】
【素养提升】
1.证明数列{an}是等差数列的两种基本方法
(1)利用定义,证明an+1-an(n∈N
)为一常数;
(2)利用等差中项,即证明2an=an-1+an+1(n≥2).
2.证明数列{an}是等比数列的两种基本方法
(1)利用定义,证明
(n∈N
)为一常数;
(2)利用等比中项,即证明
=an-1an+1(n≥2).
3.若要判断一个数列不是等差(等比)数列,只需判断存在连续三项不成等差(等
比)数列即可.
【变式训练】
1.已知数列{an}满足a1=1,nan+1=2(n+1)an.设bn=
.
(1)求b1,b2,b3;
(2)判断数列{bn}是否为等比数列,并说明理由;
(3)求{an}的通项公式.
【解析】(1)由条件可得an+1=
an.
将n=1代入得,a2=4a1,而a1=1,所以,a2=4.
将n=2代入得,a3=3a2,所以a3=12.
从而b1=1,b2=2,b3=4.
(2){bn}是首项为1,公比为2的等比数列.
由条件可得
,即bn+1=2bn,
又b1=1,所以{bn}是首项为1,公比为2的等比数列.
(3)由(2)可得
=2n-1,所以an=n·2n-1.
【加练备选】
成等差数列的三个正数的和等于15,并且这三个数分别加上2,5,13后成为
等比数列{bn}中的b3,b4,b5.
(1)求数列{bn}的通项公式;
(2)数列{bn}的前n项和为Sn,求证:数列
是等比数列.
【解析】(1)设成等差数列的三个正数分别为a-d,a,a+d.
依题意,得a-d+a+a+d=15.
解得a=5.
所以{bn}中的b3,b4,b5依次为7-d,10,18+d.
依题意,有(7-d)(18+d)=100,
解得d=2或d=-13(舍去).
故{bn}的第3项为5,公比为2.
由b3=b1·22,即5=b1·22,解得b1=
.
所以bn=b1·qn-1=
·2n-1=5·2n-3,
即数列{bn}的通项公式bn=5·2n-3.
(2)数列{bn}的前n项和Sn=
=5·2n-2-
,即Sn+
=5·2n-2.
由S1+
=2可知,
数列
是以
为首项,2为公比的等比数列.
2.设Sn为数列{an}的前n项和,对任意的n∈N
,都有Sn=2-an,数列{bn}满足
b1=2a1,bn=
(n≥2,n∈N
).
(1)求证:数列{an}是等比数列,并求{an}的通项公式;
(2)判断数列
是等差数列还是等比数列,并求数列{bn}的通项公式.
【解析】(1)当n=1时,a1=S1=2-a1,解得a1=1;
当n≥2时,an=Sn-Sn-1=an-1-an,
即
(n≥2,n∈N
).
所以数列{an}是首项为1,公比为
的等比数列,
故数列{an}的通项公式为an=
.
(2)因为a1=1,所以b1=2a1=2.
因为bn=
,
所以
,
即
(n≥2).
所以数列
是首项为
,
公差为1的等差数列.
所以
,
故数列{bn}的通项公式为bn=
.
【加练备选】
已知数列{an}满足an+1-3an=3n(n∈N
)且a1=1.设bn=
,
(1)证明数列{bn}为等差数列;
(2)设cn=
,求数列{cn}的前n项和Sn.
【解析】(1)由已知得an+1=3an+3n,得bn+1=
=bn+1,所以
bn+1-bn=1,又a1=1,所以b1=1,
所以数列{bn}是首项为1,公差为1的等差数列.
(2)bn=
=n,所以an=n·3n-1,cn=
,
所以Sn=
.
考向二 等差(等比)数列的求和
命题角度1 等差数列的通项与求和
【典例】(2020·全国Ⅲ卷)设等比数列{an}满足a1+a2=4,a3-a1=8.
(1)求{an}的通项公式;
(2)记Sn为数列{log3an}的前n项和.若Sm+Sm+1=Sm+3,求m.
【解析】(1)设等比数列{an}的公比为q,
根据题意,有
,解得
,所以an=3n-1.
(2)令bn=log3an=log33n-1=n-1,
所以Sn=
,
根据Sm+Sm+1=Sm+3,
可得
,
整理得m2-5m-6=0,因为m>0,所以m=6.
【探究延伸】
若本题的条件不变,试求数列{log3an-9}的前n项和的最小值.
【解析】依典例知an=3n-1,所以log3an-9=log33n-1-9=n-10,设其前n项和为Tn,则
Tn=
,又n∈N
,所以当n=9或10时,Tn最小,
其最小值=
=-45.
命题角度2 等比数列的通项与求和
【典例】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明
是等比数列,并求{an}的通项公式;
(2)证明:
+…+
.
【解析】(1)由an+1=3an+1得
.
又a1+
,
所以
是首项为
,公比为3的等比数列.
an+
,
因此{an}的通项公式为an=
.
(2)由(1)知
.
因为当n≥1时,3n-1≥2×3n-1,
所以
.
于是
+…+
≤1+
+…+
=
.
所以
+…+
.
【素养提升】
等差(等比)数列求和的几点注意
一是注意弄清项数;二是注意公式的适用条件;三是注意运算的准确性.
【变式训练】
1.已知数列{an}是等比数列,公比q<1,若a2=2,a1+a2+a3=7.
(1)求{an}的通项公式;
(2)设bn=log2an,求数列{bn}的前n项和.
【解析】(1)由已知得
则
或
(舍去).
所以an=4×
=23-n.
(2)因为bn=log2an=log223-n=3-n,
所以数列{bn}是首项为2,公差为-1的等差数列.
设数列{bn}的前n项和为Tn,
则Tn=
.
2.已知等差数列{an}前三项的和为-9,前三项的积为-15.
(1)求等差数列{an}的通项公式;
(2)若{an}为递增数列,求数列{|an|}的前n项和Sn.
【解析】(1)设等差数列{an}的公差为d,
则依题意得a2=-3,则a1=-3-d,a3=-3+d,
所以(-3-d)(-3)(-3+d)=-15,得d2=4,d=±2,
所以an=-2n+1或an=2n-7.
(2)由题意得an=2n-7,所以|an|=
①n≤3时,Sn=-(a1+a2+…+an)=
n
=6n-n2;
②n≥4时,Sn=-a1-a2-a3+a4+…+an=-2(a1+a2+a3)+(a1+a2+…+an)=18-6n+n2.
综上,数列{|an|}的前n项和Sn=
考向三 数列求和
命题角度1 错位相减法求和
【典例】(2020·全国Ⅰ卷)设{an}是公比不为1的等比数列,a1为a2,a3的等差中项.
(1)求{an}的公比;
(2)若a1=1,求数列{nan}的前n项和.
【解析】(1)设{an}的公比为q,
由题设得2a1=a2+a3,即2a1=a1q+a1q2.
因为a1≠0,
所以q2+q-2=0,
解得q=1(舍去),q=-2.
故{an}的公比为-2.
(2)设Sn为{nan}的前n项和.
由(1)及题设可得,an=(-2)n-1.
所以Sn=1+2×(-2)+…+n×(-2)n-1,
-2Sn=-2+2×(-2)2+…+(n-1)×(-2)n-1+n×(-2)n.
可得3Sn=1+(-2)+(-2)2+…+(-2)n-1-n×(-2)n=
-n×(-2)n.
所以Sn=
.
【探究延伸】
若例(2)中a1=1改为a1=2,结果如何?
【解析】设{nan}的前n项和为Sn,a1=2,
an=2·(-2)n-1=-(-2)n,
Sn=-[1×(-2)1+2×(-2)2+3×(-2)3+…+n(-2)n],
即-Sn=1×(-2)1+2×(-2)2+3×(-2)3+…+n(-2)n①,
2Sn=1×(-2)2+2×(-2)3+3×(-2)4+…+n(-2)n+1②,
①-②得:-3Sn=(-2)1+(-2)2+(-2)3+…+(-2)n-n·(-2)n+1
=
-n·(-2)n+1
=-
[1-(-2)n]-n·(-2)n+1,
所以Sn=
[1-(-2)n]+
(-2)n+1
=
-
(-2)n-
(-2)n
=
-
·(-2)n.
命题角度2 裂项相消法求和
【典例】在①a3+a5=5,S4=7;②4Sn=n2+3n;③5S4=14S2,a5是a3与
的等比中项,这
三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
已知Sn为等差数列{an}的前n项和,若________.?
(1)求an;
(2)记bn=
,求数列{bn}的前n项和Tn.
【解析】(1)选择条件①:设等差数列{an}的公差为d,
则
,解得
,
故an=
;
选择条件②:4Sn=n2+3n,
当n≥2时,4an=4Sn-4Sn-1=n2+3n-[(n-1)2+3(n-1)]=2n+2,即an=
(n≥2),
当n=1时,a1=S1=
=1,也适合上式,
故an=
;
选择条件③:设等差数列{an}的公差为d,
则
,
解得a1=1,d=
或a1=0,d=0(不合题意),
故an=
.
(2)因为an=
,所以bn=
=
,
故Tn=b1+b2+…+bn=2
+…+
.
【加练备选】
已知Sn为各项均为正数的数列{an}的前n项和,a1∈(0,2),
+3an+2=6Sn.
(1)求{an}的通项公式;
(2)设bn=
,数列{bn}的前n项和为Tn,若对任意的n∈N
,t≤4Tn恒成立,求实数
t的最大值.
【解析】(1)当n=1时,由
+3an+2=6Sn,得
+3a1+2=6a1,即
-3a1+2=0.
又a1∈(0,2),解得a1=1.
由
+3an+2=6Sn,可知
+3an+1+2=6Sn+1.
两式相减,得
-
+3(an+1-an)=6an+1,
即(an+1+an)(an+1-an-3)=0.
由于an>0,可得an+1-an-3=0,即an+1-an=3,
所以{an}是首项为1,公差为3的等差数列,
所以an=1+3(n-1)=3n-2.
(2)bn=
=
,
Tn=b1+b2+…+bn
=
=
.
因为Tn=
,随着n的增大而增大,所以数列{Tn}是递增数列,
所以t≤4Tn?
≤Tn?
≤T1=
?t≤1,所以实数t的最大值是1.
命题角度3 分组或并项求和
【典例】若数列{bn}对于n∈N
,都有bn+2-bn=d(常数),则称数列{bn}是公差为d的
准等差数列,如数列{cn},若cn=
则数列{cn}是公差为8的准等差
数列.设数列{an}满足a1=a,对于n∈N
,都有an+an+1=2n.
(1)求证:{an}为准等差数列;
(2)求{an}的通项公式及前20项和S20.
【解析】(1)因为an+1+an=2n,①
所以an+2+an+1=2n+2.②
由②-①得an+2-an=2(n∈N
),
所以{an}是公差为2的准等差数列.
(2)已知a1=a,an+1+an=2n(n∈N
),
所以a1+a2=2,即a2=2-a.
所以由(1)可知a1,a3,a5,…成以a为首项,2为公差的等差数列,a2,a4,a6,…成以
2-a为首项,2为公差的等差数列.
所以当n为偶数时,an=2-a+
×2=n-a,
当n为奇数时,an=a+
×2=n+a-1,
所以an=
S20=a1+a2+…+a19+a20
=(a1+a2)+(a3+a4)+…+(a19+a20)
=2×1+2×3+…+2×19=2×
=200.
【探究延伸】
题设中的条件不变,求S2n.
【解析】由典例解析可知:
S2n=(a1+a2)+(a3+a4)+(a5+a6)+…+(a2n-1+a2n)
=2×1+2×3+2×5+…+2×(2n-1)
=2×
=2n2.
【素养提升】
1.用错位相减法求和时应注意的两点
(1)要善于识别题目类型,特别是等比数列公比为负数的数列;
(2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”,以便下
一步准确写出“Sn-qSn”的表达式.
2.利用裂项相消法求和的注意事项
(1)抵消后并不一定只剩下第一项和最后一项,也有可能前面剩两项,后面也剩两
项;或者前面剩几项,后面也剩几项;
(2)裂项相消求和法是数列求和的重要方法之一,其基本形式为:若{an}是等差数
列且an≠0,则
.
3.并项求和法
一个数列的前n项和可两两结合求解,则称为并项求和.形如an=(-1)nf(n)类型,可
采用并项求和法求解.
【变式训练】
1.(2020·济宁二模)已知数列{an}是单调递增的等差数列,a1=1,且a1+2,2a2,a3+7
成等比数列.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,数列{bn}满足
=(-1)nan+1,求数列{bn}的
前n项和Tn.
【解析】(1)由题意,设{an}的公差为d,且d>0,
因为a1=1,且a1+2,2a2,a3+7成等比数列,
所以22
=(a1+2)×(a3+7),
即22(d+1)2=3×(1+2d+7),
解得d=2,d=-
(舍).
所以an=a1+2×(n-1)=2n-1.
(2)因为an=2n-1,
所以Sn=
=n2,Sn+1=(n+1)2,
所以
=n(n+1),
因为bn
=(-1)nan+1,an+1=2n+1,
所以bn=(-1)n
=(-1)n
.
当n为偶数时,Tn=-
-…
+
,
当n为奇数时,Tn=-
-…
-
.
所以当n为偶数时,Tn=-1+
;
当n为奇数时,Tn=-1-
.
2.(2019·天津高考)设{an}是等差数列,{bn}是等比数列,公比大于0,已知
a1=b1=3,b2=a3,b3=4a2+3.
(1)求{an}和{bn}的通项公式;
(2)设数列{cn}满足cn=
求a1c1+a2c2+…+a2nc2n(n∈N
).
【解析】(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,依题意,得
解得
故an=3+3(n-1)=3n,bn=3×3n-1=3n.
所以,{an}的通项公式为an=3n,{bn}的通项公式为bn=3n.
(2)a1c1+a2c2+…+a2nc2n
=(a1+a3+a5+…+a2n-1)+(a2b1+a4b2+a6b3+…+a2nbn)
=
+(6×31+12×32+18×33+…+6n×3n)
=3n2+6×(1×31+2×32+…+n×3n).
记Tn=1×31+2×32+…+n×3n, ①
则3Tn=1×32+2×33+…+n×3n+1,②
②-①得,2Tn=-3-32-33-…-3n+n×3n+1=-
+n×3n+1=
.
所以a1c1+a2c2+…+a2nc2n=3n2+6Tn=3n2+3×
=
(n∈N
).
考向四 数列的综合问题
命题角度1 数列与概率交汇问题
【典例】棋盘上标有第0,1,2,…,100站,棋子开始时位于第0站,棋手抛掷均匀硬
币走跳棋游戏.若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,
直到跳到第99站(胜利大本营)或第100站(失败集中营)时游戏结束.设棋子跳到
第n站的概率为Pn.
(1)求P3的值;
(2)证明:Pn+1-Pn=-
(Pn-Pn-1)(2≤n≤98).
【解析】(1)棋子跳到第3站有以下三种途径:连续三次掷出正面,其概率为
;
第一次掷出反面,第二次掷出正面,其概率为
;
第一次掷出正面,第二次掷出反面,其概率为
,因此P3=
.
(2)(用构造法证明)易知棋子先跳到第n-2站,再掷出反面,其概率为
Pn-2;
棋子先跳到第n-1站,再掷出正面,其概率为
Pn-1,因此有Pn=
(Pn-1+Pn-2),
即Pn-Pn-1=-
(Pn-1-Pn-2),
也即Pn+1-Pn=-
(Pn-Pn-1)(2≤n≤98).
命题角度2 数列与函数、不等式的交汇问题
【典例】若数列{an}的前n项和为Sn,点(an,Sn)在y=
-
x的图象上(x∈N
).
(1)求数列{an}的通项公式;
(2)若c1=0,且对任意正整数n都有cn+1-cn=
an,求证:对任意正整数n≥2,总
有
.
【解析】(1)因为Sn=
-
an,
所以当n≥2时,an=Sn-Sn-1=
an-1-
an,
所以an=
an-1,
又因为S1=
-
a1,所以a1=
,
所以an=
.
(2)由cn+1-cn=
=2n+1,得当n≥2时,
cn=c1+(c2-c1)+(c3-c2)+…+(cn-cn-1)=0+3+5+…+(2n-1)=n2-1=(n+1)(n-1).
所以
=
=
.
又因为
,所以原式得证.
【素养提升】
1.解决数列与函数综合问题的注意点
(1)数列是一类特殊的函数,其定义域是正整数集,而不是某个区间上的连续实数,
所以它的图象是一群孤立的点.
(2)转化以函数为背景的条件时,应注意题中的限制条件,如函数的定义域,这往
往是非常容易忽视的问题.
(3)利用函数的方法研究数列中相关问题时,应准确构造函数,注意数列中相关限
制条件的转化.
2.数列中不等式问题的处理方法
(1)函数法:即构造函数,通过函数的单调性、极值等得出关于正实数的不等式,
通过对关于正实数的不等式特殊赋值得出数列中的不等式.
(2)放缩法:数列中不等式可以通过对中间过程或最后的结果放缩得到.
(3)比较法:作差或者作商比较法.
【变式训练】
已知函数f(x)的图象过定点(1,1),且对任意的实数x1,x2∈R,都有
f(x1+x2)=1+f(x1)+f(x2).
(1)证明数列
(n∈N
)为等比数列;
(2)若bn=
,数列{bn}的前n项和为Tn,不等式T2n-Tn>
log2(x+1)(n≥2,n∈N
)
恒成立,求实数x的取值范围.
【解析】(1)令x1=x2=
,则
,
即f
=1+2f
,
则f
+1=2
,
令x1=x2=
,因为函数f(x)的图象过定点(1,1),所以f(1)=1+2f
=1,得f
=0,所以数列
是等比数列,公比为
,首项为1.
(2)由题意知函数f(x)的图象过定点(1,1),
所以f(1)=1.
令x1=n,x2=1,
则f(n+1)=1+f(1)+f(n),
即f(n+1)=f(n)+2,
则{f(n)}是等差数列,公差为2,首项为1,
故f(n)=1+(n-1)·2=2n-1.
因为bn=
,所以bn=
=
.
设g(n)=T2n-Tn=bn+1+bn+2+…+b2n=
,
则g(n+1)-g(n)=
=
>0,
所以{g(n)}是递增数列,g(n)min=g(2)=
+
=
,
从而
log2(x+1)<
,即log2(x+1)<2,则
解得x∈(-1,3),
所以实数x的取值范围为(-1,3).
专题能力提升练
八 数列求和及数列的综合应用
(40分钟 80分)
1.已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1=-1,
b1=1,a2+b2=3.
(1)若a3+b3=7,求{bn}的通项公式;
(2)若T3=13,求Sn.
【解析】(1)设数列{an}的公差为d,数列{bn}的公比为q,
则an=-1+(n-1)d,bn=qn-1.
由a2+b2=3,得d+q=4,(
)
由a3+b3=7,得2d+q2=8,(
)
联立(
)(
),解得q=2或q=0(舍去),
因此数列{bn}的通项公式为bn=2n-1.
(2)因为T3=1+q+q2,所以1+q+q2=13,
解得q=3或q=-4,
由a2+b2=3,得d=4-q,所以d=1或d=8.
由Sn=na1+
n(n-1)d,
得Sn=
n2-
n或Sn=4n2-5n.
2.设Sn为数列{an}的前n项和,已知a3=7,an=2an-1+a2-2(n≥2).
(1)证明:数列{an+1}为等比数列;
(2)求数列{an}的通项公式,并判断n,an,Sn是否成等差数列.
【解析】(1)因为a3=7,a3=3a2-2,所以a2=3,
所以an=2an-1+1,
所以a1=1,
=2(n≥2),
所以数列{an+1}是首项为a1+1=2,公比为2的等比数列.
(2)由(1)知,an+1=2n,所以an=2n-1,
所以Sn=
-n=2n+1-n-2,所以n+Sn-2an=n+(2n+1-n-2)-2(2n-1)=0,
所以n+Sn=2an,
即n,an,Sn成等差数列.
【加练备选】
设数列{an}的前n项和为Sn,n∈N
.已知a1=1,a2=
,a3=
,且当n≥2时,
4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明:{an+1-
an}为等比数列;
(3)求数列{an}的通项公式.
【解析】(1)当n=2时,4S4+5S2=8S3+S1,
即
解得:a4=
.
(2)因为4Sn+2+5Sn=8Sn+1+Sn-1(n≥2),
所以4Sn+2-4Sn+1+Sn-Sn-1=4Sn+1-4Sn(n≥2),即4an+2+an=4an+1(n≥2),
因为4a3+a1=4×
+1=6=4a2,
所以4an+2+an=4an+1,
因为
所以数列
是以a2-
a1=1为首项,公比为
的等比数列.
(3)由(2)知,
是以1为首项,公比为
的等比数列,
所以an+1-
an=
.
即
所以
是以
=2为首项,4为公差的等差数列,
所以
=2+(n-1)×4=4n-2,即an=(4n-2)×
=(2n-1)×
.
所以数列{an}的通项公式是an=(2n-1)×
.
3.(2020·临沂二模)已知数列{an}满足a1=2,(n+2)an=(n+1)an+1-2(n2+3n+2),设
bn=
.
(1)证明数列{bn}是等差数列;
(2)设
=2n+1,求数列{cn}的前n项和Tn(n∈N
).
【解析】(1)因为a1=2,所以b1=
=1.
将(n+2)an=(n+1)an+1-2(n2+3n+2)两边同时除以(n+1)(n+2)得:
所以
=2,即bn+1-bn=2.
所以数列{bn}是以1为首项,2为公差的等差数列.
(2)由(1)得bn=1+2(n-1)=2n-1.
因为
=2n+1,
所以cn=(2n+1)bn=(2n-1)·2n+2n-1.
设Pn=1×2+3×22+5×23+…+(2n-1)·2n,
2Pn=1×22+3×23+…+(2n-3)·2n+(2n-1)·2n+1,
两式相减得:-Pn=2+2(22+23+…+2n)-(2n-1)·2n+1
化简得Pn=6+(2n-3)·2n+1.
设Sn=1+3+5+…+(2n-1)=
=n2,所以Tn=Pn+Sn=6+(2n-3)·2n+1+n2.
4.已知等差数列{an}的前n项和为Sn,{bn}是各项均为正数的等比数列,a1=b4,________,b2=8,b1-3b3=4,是否存在正整数k,使得数列
的前k项和
Tk>
?若存在,求出k的最小值;若不存在,说明理由.?
从①S4=20,②S3=2a3,③3a3-a4=b2这三个条件中任选一个,补充到上面问题中并作
答.
(注:如果选择多个条件分别解答,按第一个解答计分.)
【解析】设等比数列{bn}的公比为q(q>0),则b1=
,b3=8q,于是
-3×8q=4,即
6q2+q-2=0,
解得q=
,q=-
(舍去).
若选①:则a1=b4=2,S4=4a1+
d=20,解得d=2,
所以
令1-
>
,解得k>15,
因为k为正整数,所以k的最小值为16.
若选②:则a1=b4=2,3a1+
d=2(a1+2d),解得d=2.
下同①.
若选③:则a1=b4=2,3(a1+2d)-(a1+3d)=8,解得d=
.
于是
于是
令Tk>
,得
<
,
注意到k为正整数,解得k≥7,所以k的最小值为7.
5.(2020·新高考全国Ⅰ卷)已知公比大于1的等比数列{an}满足a2+a4=20,a3=8.
(1)求{an}的通项公式;
(2)记bm为{an}在区间(0,m](m∈N
)中的项的个数,求数列{bm}的前100项和S100.
【命题意图】本题考查等比数列通项公式的应用,考查数列基本量的运算求解能力.体现了数学运算与数学抽象的核心素养.
【解析】(1)设{an}的公比为q.
由题设得a1q+a1q3=20,a1q2=8.
解得q=
(舍去),或q=2,a1=2.
所以{an}的通项公式为an=2n.
(2)由题设及(1)知b1=0,且当2n≤m<2n+1时,bm=n.
所以
S100=b1+(b2+b3)+(b4+b5+b6+b7)+…+(b32+b33+…+b63)+(b64+b65+…+b100)=0+1×2+2×22
+3×23+4×24+5×25+6×(100-63)=480.
6.已知数列{an}满足an=3an-1+k3n-1(n∈N
,n≥2,k∈R).
(1)设a1=1,k=0,证明数列{an-
}是等比数列;
(2)对任意k∈R,是否存在一个实数t,使得bn=
(an+t)(n∈N
)且{bn}为等差数列?
若存在,求出t的值;若不存在,请说明理由.
【解析】(1)当k=0时,an=3an-1-1,
所以
又a1-
=
≠0,所以数列
是首项为
,公比为3的等比数列.
(2)当n≥2时,bn-bn-1
=
(an+t)-
(an-1+t)
=
(an+t-3an-1-3t)
=
(3an-1+k3n-1+t-3an-1-3t)
=
(k3n-1-2t)=k-
.
要使{bn}为等差数列,则必须使1+2t=0,
所以t=-
,
即对任意的k∈R,存在t=-
,使{bn}为等差数列.
【加练备选】
已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.
(1)求数列{xn}的通项公式;
(2)如图,在平面直角坐标系xOy中,依次连接点P1(x1,1),P2(x2,2),…,Pn+1(xn+1,n+1)得到折线P1
P2…Pn+1,求由该折线与直线y=0,x=x1,x=xn+1所围成的区域的面积Tn.
【解析】(1)设数列{xn}的公比为q,
由题意得
所以3q2-5q-2=0.
因为q>0,
所以q=2,x1=1,
因此数列{xn}的通项公式为xn=2n-1.
(2)过P1,P2,…,Pn+1向x轴作垂线,垂足分别为Q1,Q2,…,Qn+1.
由(1)得xn+1-xn=2n-2n-1=2n-1,
记梯形PnPn+1Qn+1Qn的面积为bn,
由题意得bn=
×2n-1=(2n+1)×2n-2,
所以Tn=b1+b2+…+bn
=3×2-1+5×20+7×21+…+(2n-1)×2n-3+(2n+1)×2n-2.(i)
又2Tn=3×20+5×21+7×22+…+(2n-1)×2n-2+(2n+1)×2n-1.(ii)
(i)-(ii)得-Tn=3×2-1+(2+22+…+2n-1)-(2n+1)×2n-1=
-(2n+1)×2n-1.
所以Tn=
.
7.已知等比数列{an}的公比q>1,a1=2,且a1,a2,a3-8成等差数列,数列{anbn}的前n
项和为
.
(1)分别求出数列{an}和{bn}的通项公式;
(2)设数列
的前n项和为Sn,已知?n∈N
,Sn≤m恒成立,求实数m的最小值.
【解析】(1)因为a1=2,且a1,a2,a3-8成等差数列,
所以2a2=a1+a3-8,
即2a1q=a1+a1q2-8,
所以q2-2q-3=0,
所以q=3或-1,而q>1,
所以q=3,
所以an=2·3n-1.
因为a1b1+a2b2+…+anbn=
,
所以a1b1+a2b2+…+an-1bn-1
=
,
两式相减得anbn=2n·3n-1(n≥2).
因为an=2·3n-1,所以bn=n(n≥2),
令n=1,可得b1=1,所以bn=n.
(2)因为数列{an}是首项为2,公比为3的等比数列,
所以数列
是首项为
,公比为
的等比数列,
所以
因为?n∈N
,Sn≤m恒成立,
故实数m的最小值为
.
【加练备选】
已知数列{an}满足a1=
,an+1an=2an+1-1(n∈N
),令bn=an-1.
(1)求数列{bn}的通项公式;
(2)令cn=
,求证:c1+c2+…+cn
【解析】(1)因为an+1an=2an+1-1(n∈N
),bn=an-1,即an=bn+1.
所以(bn+1+1)(bn+1)=2(bn+1+1)-1,
化为:
因为a1=
,所以b1=a1-1=-
,
所以
=-2,所以数列
是等差数列,首项为-2,公差为-1.
所以
=-2-(n-1)=-1-n,
所以bn=-
.
(2)由(1)可得:an=bn+1=1-
.
所以
因为n≥2时,2n+2≤2n+1-1,
所以
所以c1+c2+…+cn<
8.设函数fn(x)=x-(3n-1)x2(其中n∈N
),区间In={x|fn(x)>0}.
(1)定义区间(α,β)的长度为β-α,求区间In的长度;
(2)把区间In的长度记作数列{an},
令bn=an·an+1,
①求数列{bn}的前n项和Tn;
②是否存在正整数m,n(1
解得0
.
所以区间的长度为
-0=
.
(2)由(1)知an=
.
①因为bn=an·an+1=
,
所以Tn=b1+b2+…+bn
②由①知T1=
,Tm=
,
Tn=
.
假设存在正整数m,n(1
化简得
所以(-3m2+6m+2)n=5m2.(
)
当m=2时,(
)式可化为2n=20,所以n=10.
当m≥3时,-3m2+6m+2=-3(m-1)2+5≤-7<0.
又因为5m2>0,所以(
)式可化为
n=
<0,此时n无正整数解.
综上,存在正整数m=2,n=10满足条件.
同课章节目录
