三角恒等变换与解三角形 课件(共104张PPT)2021届高考数学二轮复习
文档属性
| 名称 | 三角恒等变换与解三角形 课件(共104张PPT)2021届高考数学二轮复习 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 22:16:13 | ||
图片预览



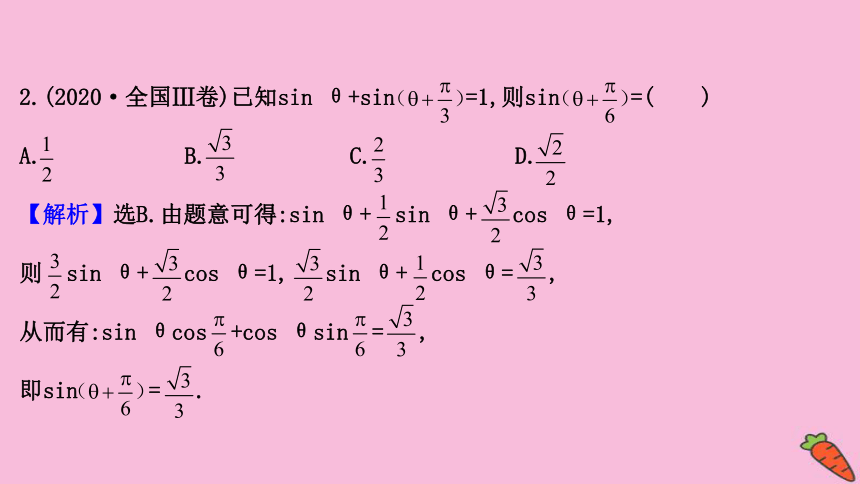



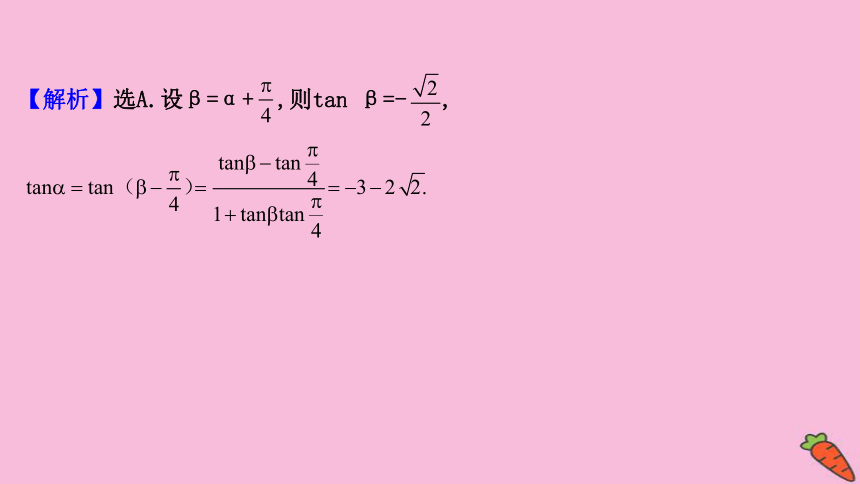

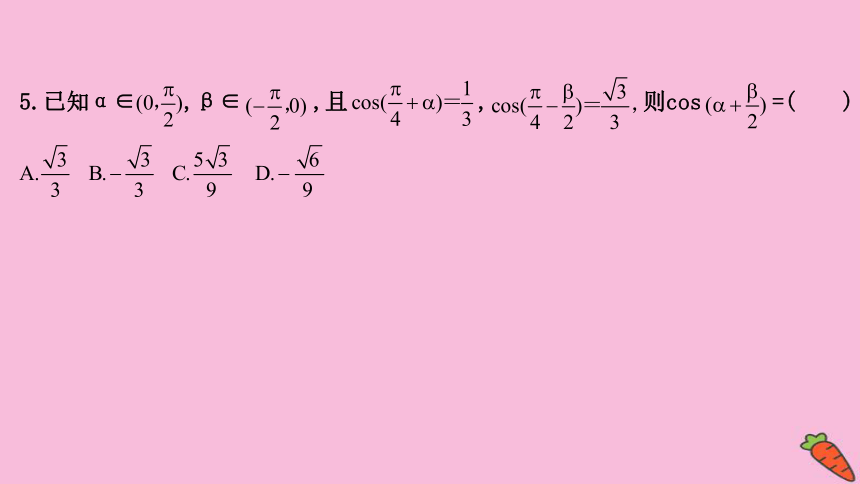
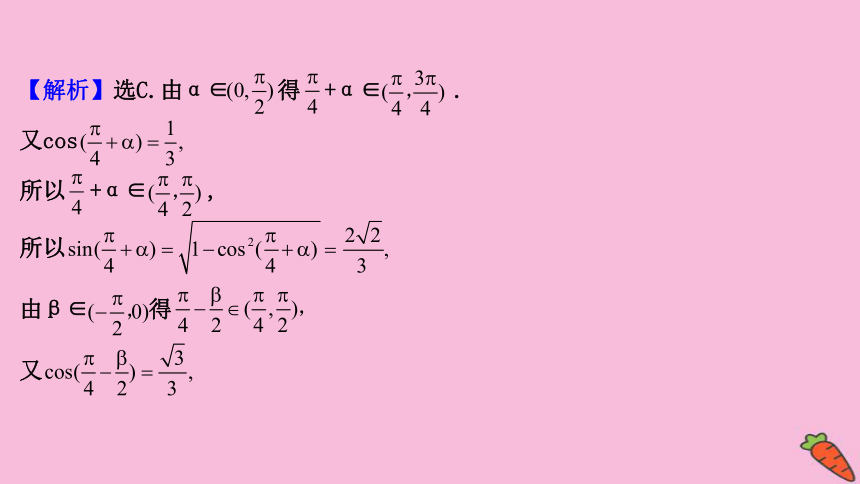
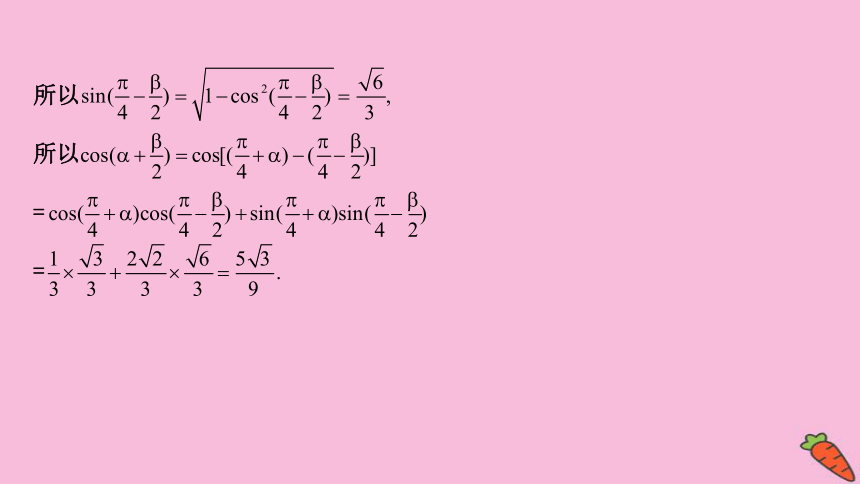
文档简介
(共104张PPT)
三角恒等变换与解三角形
关键能力·应用实践
考向一 三角恒等变换
【多维题组】速通关
1.函数y=lg
的零点是x1=tan
α和x2=tan
β,则tan
=( )
A.
B.-
C.
D.-
【解析】选C.因为函数y=lg
的零点是x1=tan
α和x2=tan
β,
所以tan
α和tan
β是方程x2+5x+4=1的两个实数根,
所以tan
α+tan
β=-5,tan
αtan
β=3,
所以
2.(2020·全国Ⅲ卷)已知sin
θ+sin
=1,则sin
=( )
A.
B.
C.
D.
【解析】选B.由题意可得:sin
θ+
sin
θ+
cos
θ=1,
则
sin
θ+
cos
θ=1,
sin
θ+
cos
θ=
,
从而有:sin
θcos
+cos
θsin
=
,
即sin
=
.
【加练备选】
(2020·全国Ⅰ卷)已知α∈(0,π),且3cos
2α-8cos
α=5,则sin
α
=( )
A.
B.
C.
D.
【解析】选A.3cos
2α-8cos
α=5,
得6cos2α-8cos
α-8=0,
即3cos2α-4cos
α-4=0,
解得cos
α=-
或cos
α=2(舍去),
又因为α∈(0,π),所以sin
α=
3.已知角α的顶点在坐标原点,始边与x轴的正半轴重合,将角α的终边按逆时针方向旋转
后经过点
,则tan
α=( )
A.-3-2
B.-3+2
C.-1
D.1
【解析】选A.设β=α+
,则tan
β=-
,
4.(2020·全国Ⅱ卷)若sin
x=-
,则cos
2x=______.?
【解析】cos
2x=1-2sin2x=1-2×
答案:
5.已知α∈
,β∈
,且
,
则cos
=( )
【解析】选C.由α∈
得
+α∈
.
又cos
所以
+α∈
,
所以
由β∈
得
又
所以
所以
=
=
【加练备选】
(2020·聊城二模)已知cos(α+
)=
,α∈
,则sin
=________.?
【解析】因为
α∈
所以
所以
则
答案:
【技法点拨】提素养
三角函数求值的类型及方法
(1)“给角求值”:利用观察得到的关系,结合三角函数公式转化为特殊角的三角函数,有时,虽不能转化为特殊角,但可通过分子分母的约分、正负项的相互抵消达到化简求值的目的.
(2)“给值求值”:关键在于“变角”,使其角相同或具有某种关系.
(3)“给值求角”:关键也是变角,把所求角用含已知角的式子表示,由所得的函数值结合该函数的单调区间求得角,有时要压缩角的取值范围.
考向二 利用正弦、余弦定理解三角形
【多维题组】速通关
1.(2020·全国Ⅲ卷)在△ABC中,cos
C=
,AC=4,BC=3,则cos
B=( )
【解析】选A.设AB=c,BC=a,CA=b,
因为c2=a2+b2-2abcos
C=9+16-2×3×4×
=9,
所以c=3,cos
B=
【加练备选】
(2020·全国Ⅲ卷)在△ABC中,cos
C=
,AC=4,BC=3,则tan
B=( )
A.
B.2
C.4
D.8
【解析】选C.设AB=c,BC=a,CA=b,因为c2=a2+b2-2abcos
C=9+16-2×3×4×
=9,
所以c=3,cos
B=
所以
所以tan
B=4
.
2.(多选题)在△ABC中,角A,B,C所对的边分别为a,b,c,下列结论正确的是( )
A.a2=b2+c2-2bccos
A
B.asin
B=bsin
A
C.a=bcos
C+ccos
B
D.acos
B+bcos
A=sin
C
【解析】选ABC.由在△ABC中,角A,B,C所对的边分别为a,b,c,知:
在A中,由余弦定理得:a2=b2+c2-2bccos
A,故A正确;
在B中,由正弦定理得:
所以asin
B=bsin
A,故B正确;
在C中,由余弦定理得:bcos
C+ccos
B=
故C正确;
在D中,由余弦定理得acos
B+bcos
A=
≠sin
C,故D
错误.故选ABC.
3.(2019·全国Ⅰ卷)△ABC的内角A,B,C的对边分别为a,b,c,已知asin
A-bsin
B
=4csin
C,cos
A=-
,则
=( )
A.6
B.5
C.4
D.3
【解析】选A.由已知及正弦定理可得a2-b2=4c2,由余弦定理推论可得-
=cos
A
=
,所以
所以
所以
×4=6.
4.(2020·南昌二模)已知梯形ABCD中,AD∥BC,AD=
,AB=4,∠ABC=60°,
∠ACB=45°,则DC=________.?
【解析】因为在△ABC中,∠ABC=60°,∠ACB=45°,
AB=4,所以由正弦定理
可得
所以
因为AD∥BC,所以∠ACB=∠DAC=45°,
所以在△ACD中,由余弦定理可得
答案:
【加练备选】
在△ABC中,已知AC=
,∠ABC=60°,AB,则BC
边上的高等于________.?
【解析】设a,b,c分别为角A,B,C的对边,因为∠ABC=60°且△ABC的面积为
,
所以
acsin
60°=
,即ac=6①
又AC=
,所以b2=a2+c2-2accos
60°=7,
即a2+c2-ac=7②
联立①②结合a>c解得:a=3,c=2.
设BC边上的高为h,所以
ah=
×3×h=
.
所以h=
.
答案:
【变式拓展】
本题条件改为“AC=3,AB=3
,∠ABC=30°,BC>AC”,求AC边上的高.
【解析】设角A,B,C的对边分别为a,b,c.
因为AC=3,AB=3
,∠ABC=30°,
所以b=3,c=3
,B=30°,
所以由余弦定理b2=a2+c2-2accos
B,
可得9=a2+27-2×a×3
×
,
整理可得a2-9a+18=0,又a>b,所以a=6.
因为S△ABC=
acsin
B=
,
所以AC边上的高的长为
5.(2020·全国Ⅰ卷)如图,在三棱锥P–ABC的平面展开图中,AC=1,AB=AD=
,
AB⊥AC,AB⊥AD,∠CAE=30°,则cos∠FCB=______.?
【解析】因为AB⊥AC,AB=
,AC=1,
由勾股定理得BC=
=2,
同理得BD=
,所以BF=BD=
,
在△ACE中,AC=1,AE=AD=
,∠CAE=30°,
由余弦定理得CE2=AC2+AE2-2AC·AEcos30°=1+3-2×1×
×
=1,
所以CF=CE=1,在△BCF中,BC=2,BF=
,CF=1,
由余弦定理得cos∠FCB=
答案:-
【技法点拨】提素养
解三角形的常见题型及求解方法
(1)已知两角A,B与一边a,由A+B+C=π及
可先求出角C及b,
再求出c.
(2)已知两边b,c及其夹角A,由a2=b2+c2-2bccos
A,先求出a,再求出角B,C.
(3)已知三边a,b,c,由余弦定理可求出角A,B,C.
(4)已知两边a,b及其中一边a的对角A,由正弦定理
可求出另一边b的
对角B,由C=π-(A+B),可求出角C,再由
可求出c,而通过
求角B时,可能有一解或两解或无解的情况.
考向三 正弦、余弦定理的实际应用
(重难突破)
【多维题组】速通关
1.如图所示,为了测量A,B两座岛屿间的距离,小船从初始位置C出发,已知A在C的
北偏西45°的方向上,B在C的北偏东15°的方向上,现在船往东开2百海里到达E
处,此时测得B在E的北偏西30°的方向上,再开回C处,由C向西开2
百海里到达
D处,测得A在D的北偏东22.5°的方向上,则A,B两座岛屿间的距离为( )
A.3百海里
B.3
百海里
C.4百海里
D.4
百海里
【考场思维】
解题方法
直接计算
解题流程
利用方向角求出三角形中各个角的大小→利用正弦定理求出AC和BC→利用余弦定理求出结果.
素养考查
数学运算、直观想象
【解析】选B.根据题意知:∠ADC=∠DAC=67.5°,
∠ACB=60°,DC=2
,CE=2,∠BCE=75°,∠CBE=45°,∠CEB=60°.
所以在△BCE中,利用正弦定理
解得BC=
,
在△ADC中,∠ADC=∠DAC=67.5°,
所以DC=AC=2
,
则在△ACB中,利用余弦定理AB2=AC2+CB2-2AC·CB·cos
60°,解得AB=3
,
所以A,B两座岛屿的距离为3
百海里.
2.某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射
高度:在C处(点C在水平地面下方,O为CH与水平地面ABO的交点)进行该仪器的垂
直弹射,水平地面上两个观察点A,B两地相距100米,∠BAC=60°,其中A到C的距离
比B到C的距离远40米.A地测得该仪器在C处的俯角为∠OAC=15°,A地测得最高点
H的仰角为∠HAO=30°,则该仪器的垂直弹射高度CH为( )
A.210(
+
)米
B.140
米
C.210
米
D.20(
-
)米
【考场思维】
解题方法
建立方程求解
解题流程
设AC=x米,则BC=(x-40)米→在△ABC内,由余弦定理构建方程求出AC→在△ACH中,用正弦定理求CH.
素养考查
数学运算、直观想象
【解析】选B.由题意,设AC=x米,则BC=(x-40)米,在△ABC内,由余弦定理得
BC2=BA2+CA2-2BA·CA·cos∠BAC,
即(x-40)2=x2+10
000-100x,解得x=420.
在△ACH中,AC=420米,
∠CAH=30°+15°=45°,∠CHA=90°-30°=60°,
由正弦定理
可得CH=AC·
=140
(米).
【技法点拨】提素养
解三角形实际应用问题的步骤
【变式训练】
1.为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积为( )
A.
km2
B.
km2
C.
km2
D.
km2
【解析】选D.如图,连接AC,根据余弦定理可得AC=
,故△ABC为直角三角形,
且∠ACB=90°,∠BAC=30°,从而△ADC为等腰三角形,且∠ADC=150°,设AD=DC=x,
根据余弦定理得x2+x2+
x2=3,即x2=
所以所求小区的面积为
×1×
+
×3(2-
)×
=
(km2).
2.《海岛算经》是中国学者刘徽编撰的一部测量数学著作,现有取自其中的一个
问题:今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表参相直,从前
表却行一百二十三步,人目着地,取望岛峰,与表末参合,从后表却行一百二十七
步,人目着地,取望岛峰,亦与表末参合,问岛高几何?其大意为:如图所示,立两个
三丈高的标杆BC和DE,两标杆之间的距离BD=1
000步,两标杆的底端与海岛的底
端H在同一直线上,从前面的标杆B处后退123步,人眼贴地面,从地上F处仰望岛
峰,A,C,F三点共线,从后面的标杆D处后退127步,人眼贴地面,从地上G处仰望岛
峰,A,E,G三点也共线,则海岛的高为(注:1步=6尺,1里=180丈=1
800尺=300步)
( )
A.1
255步
B.1
250步
C.1
230步
D.1
200步
【解析】选A.因为AH∥BC,所以△BCF∽△HAF,所以
因为AH∥DE,
所以△DEG∽△HAG,所以
又BC=DE,所以
即
所以HB=30
750步,
又
所以AH=
=1
255(步).
3.如图所示,在山脚A测得山顶P的仰角为∠QAP=45°,沿倾斜角为∠QAB=15°的
斜坡向上走146.4米到达B,在B测得山顶P的仰角为∠CBP=60°,则山高PQ约为
________米.?(
≈1.414,
≈1.732,结果保留到小数点后1位)
【解析】∠PAB=∠PAQ-∠BAQ=45°-15°=30°,
∠APB=∠QPA-∠CPB=45°-(90°-60°)=15°.
∠ABP=180°-(∠PAB+∠APB)=135°,
在△PAB中,由正弦定理得
即
PQ=APsin∠PAQ=
≈282.8(米).
答案:282.8
【加练备选】
已知在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.轮船沿BC行驶一段时间后,到达海岛的正西方向的D处,此时轮船距岛A有________千米.?
【解析】由已知可求得AB=
,AC=
,BC=
,
所以sin∠ACB=
,cos∠ACB=
,则∠ACB为锐角,∠ACD为钝角,
且sin∠ACD=
,cos∠ACD=-
.
在△ACD中,sin∠ADC=sin(∠ACD+∠DAC)
=sin∠ACDcos∠DAC+sin∠DACcos∠ACD
由正弦定理可求得AD=
答案:
题组训练·素养提升
【新题速递】
1.已知角α的顶点在坐标原点O,始边与x轴的非负半轴重合,将角α的终边绕O点
顺时针旋转
后,经过点(-3,4),则sin
α=( )
A.
B.
C.
D.-
【解析】选B.角α的终边按顺时针方向旋转
后得到的角为α-
,
所以由三角函数的定义,可得:
所以sin
α=sin
2.(2020·青岛模拟)若函数f(x)=sin
2xsin
φ+2cos2xcos
φ-cos
φ
的一个极大值点为
,则φ=( )
A.0
B.
C.
D.
【解析】选D.f(x)=sin
2xsin
φ+2cos2xcos
φ-cos
φ=sin
2xsin
φ+
(2cos2x-1)cos
φ=sin
2xsin
φ+cos
2xcos
φ=cos
,因为f(x)的一
个极大值点为
,所以f
=cos
=1,解得φ=
+2kπ,k∈Z,又0<φ<π,
故φ=
.
3.2020年5月27日,中国珠穆朗玛峰测高工程队顺利登顶,将在峰顶竖立站标,安装GNSS(全球卫星导航系统),将对这座世界最高峰的高度进行最新测量,如在水平面上的A处测得峰顶H的仰角是45°,然后在另一点B处测得峰顶H的仰角是60°,若H在水平面的射影为O(如图),且∠AOB=150°,AB=a,则珠穆朗玛峰的最新高度OH=________.?
【解析】设OH=h,由题可知:∠OAH=45°,∠OBH=60°,
则AO=h,BO=
h,
在△AOB中,有AB2=AO2+BO2-2AO·BO·cos∠AOB,
又AB=a,所以a2=h2+
-2h·
·cos
150°,
则h2=
?h=
a.
答案:
a
4.(2020·大庆三模)已知函数f(x)=2sin2x+
asin
2x的最大值为3,则实数a的
值为________.?
【解析】由题得f(x)=2sin2x+
asin
2x=1-cos
2x+
asin
2x
=
sin(2x+φ)+1,其中tan
φ=-
,
所以f(x)的最大值为
+1=3,解得a=±1.
答案:±1
5.在△ABC中,角A,B,C所对的边分别为a,b,c.已知a=2
,b=5,c=
.则
C=________;sin
=________.?
【解析】在△ABC中,由a=2
,b=5,c=
及余弦定理得
又因为C∈(0,π),所以C=
.
在△ABC中,由C=
,a=2
,c=
及正弦定理,
可得
由aA=
,
可得
进而sin
2A=2sin
Acos
A=
cos
2A=2cos2A-1=
,
所以sin
=sin
2Acos
+cos
2Asin
=
答案:
【创新迁移】
1.有一道题目由于纸张破损,有一条件看不清楚,具体如下:“在△ABC中,角
A,B,C的对边分别为a,b,c,已知a=
,________,c2-b2-3c+3=0,求角A.”经推断,
破损处的条件为三角形一边的长度,且该题的答案A=
是唯一确定的,则破损处
应是________.?
【解析】因为c2-b2-3c+3=0,a=
.
所以c2-b2-
ac+a2=0,
即
所以cos
B=
,又B∈(0,π),所以B=
.
(1)由正弦定理可知,
可得b=
.
检验:
又因为A∈(0,π)且a>b,
所以A=
或者A=
,这与已知角A的解为唯一解矛盾.
(2)B=
,A=
,所以C=
,
由正弦定理可知,
检验:
又A∈(0,π),且c>a,
所以A=
.故应填的条件是:c=
答案:c=
2.顶角为36°的等腰三角形称为“黄金三角形”,黄金三角形看起来标准又美观.
如图所示,△ABC是黄金三角形,AB=AC,作∠ABC的平分线交AC于点D,易知△BCD也
是黄金三角形.若BC=1,则AB=______;借助黄金三角形可计算sin
234°=______.?
【解析】由题可得∠A=∠ABD=∠DBC=36°,∠C=∠BDC=72°,所以△ABC∽△BCD,
得
,且AD=BD=BC=1.
设AB=AC=x,则CD=x-1,所以
,
可解得x=
(负值舍去),所以AB=
因为sin
234°=sin(180°+54°)=-sin
54°=-cos
36°.
在△ABC中,根据余弦定理可得cos
36°=
所以sin
234°=-
.
答案:
-
专题能力提升练
五 三角恒等变换与解三角形
(40分钟 80分)
一、选择题(共12小题,每小题5分,共60分)
1.若cos
78°=m,则sin(-51°)=( )
【解析】选A.因为cos
78°=m,
所以cos(180°-78°)=cos
102°
=-cos
78°=-m,
可得1-2sin251°=cos
102°=-m,
所以sin251°=
,解得:sin
51°=
,
所以sin(-51°)=
.
2.在△ABC中,角A,B,C所对的边分别为a,b,c,若b=2
,c=3,B=2C,则cos
2C的值为( )
【解析】选B.由正弦定理可得,
,
所以
又b=2
,c=3,所以2cos
C=
,cos
C=
,
所以cos
2C=2cos2C-1=2×
-1=
.
3.
=( )
A.1
B.2
C.
D.
【解析】选C.原式=
4.已知α为锐角,β为第二象限角,且cos(α-β)=
,sin(α+β)=
,则sin(3α-β)=( )
【解析】选B.因为α为锐角,β为第二象限角,cos(α-β)>0,sin(α+β)>0,
所以α-β为第四象限角,α+β为第二象限角,
因此sin(α-β)=-
,cos(α+β)=-
,所以sin
2α=sin(α-β+α+β)
=sin
(α-β)cos
(α+β)+cos
(α-β)sin
(α+β)
=
=1.
因为α为锐角,所以2α=
,
所以sin(3α-β)=sin(2α+α-β)=cos(α-β)=
.
【一题多解】解答本题还可以有如下解法:
由上面可得,sin(α-β)=-
,cos(α+β)=-
.
所以cos2(α-β)=2cos2(α-β)-1
=2×
,
sin2(α-β)=2sin(α-β)cos(α-β)
=2×
.
所以sin(3α-β)=sin[2(α-β)+(α+β)]
=sin
2(α-β)·cos(α+β)+cos
2(α-β)·sin(α+β)
=
.
5.函数f(x)=2sin2ωx+sin
2ωx-1的图象向左平移
个单位长度后,与原图象有
相同的对称轴,则正实数ω的最小值是( )
A.1
B.2
C.4
D.6
【解析】选B.因为f(x)=2sin2ωx+sin
2ωx-1=sin
2ωx-cos
2ωx
=
sin
,
将其图象向左平移
个单位长度后,
可得y=
sin
=
sin
的图象.
由于所得的图象与原图象有相同的对称轴,
所以
=kπ,k∈Z,即ω=2k,k∈Z,
则正实数ω的最小值为2.
6.在△ABC中,cos2
=
(a,b,c分别为角A,B,C的对边),则△ABC的形状为
( )
A.正三角形
B.直角三角形
C.等腰三角形或直角三角形
D.等腰直角三角形
【解析】选B.因为cos2
=
,
所以
,
所以
,化简得a2+b2=c2.
故△ABC是直角三角形.
7.(多选题)下列选项中,值为
的是( )
A.cos
72°cos
36°
B.
C.
D.
【解析】选AB.对于A,cos
36°cos
72°
故A正确;
对于B,
故B正确;
对于C,原式=
故C错误;
对于D,
-
cos215°=-
(2cos215°-1)
=-
cos
30°=-
,故D错误.
8.(2020·中卫二模)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知
C=
,sin
B=3sin
A,若△ABC的面积为6
,则c=( )
【解题导引】由sin
B=3sin
A可得b=3a,再利用面积公式得到a,b的方程组,解出
a,b,最后利用余弦定理求出c的值.
【解析】选B.因为sin
B=3sin
A,所以b=3a,
又因为C=
,△ABC的面积为6
,
所以S=
absin
C=
a2×sin
=6
,
解得a=2
,b=6
,
所以c2=a2+b2-2abcos
C=
=104.
所以c=2
.
【加练备选】
在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若sin
A=
,a=2,S△ABC=
,
则b的值为( )
【解析】选A.由S△ABC=
bcsin
A=
bc×
=
,解得bc=3.
因为A为锐角,sin
A=
,所以cos
A=
,
由余弦定理得a2=b2+c2-2bccos
A,代入数据解得b2+c2=6,则(b+c)2=12,b+c=2
,
所以b=c=
.
9.(2020·郑州三模)在△ABC中,角A,B,C所对的边分别为a,b,c.
若
asin
B=c-bcos
A,则角B等于( )
【解析】选A.因为
asin
B=c-bcos
A,
所以由正弦定理可得
sin
Asin
B=sin
C-sin
Bcos
A,
所以
sin
Asin
B+sin
Bcos
A=sin
C,
因为sin
C=sin(A+B)
=sin
Acos
B+cos
Asin
B,
所以
sin
Asin
B=sin
Acos
B,因为sin
A≠0,
所以
sin
B=cos
B,可得tan
B=
,
因为B∈(0,π),所以B=
.
10.如图所示,位于A处的信息中心获悉:在其正东方向相距30
海里的B处有一
艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西45°、相距
20海里的C处的乙船,现乙船朝北偏东θ的方向沿直线CB前往B处救援,则cos
θ
的值为( )
【解析】选B.在△ABC中,AB=30
,
AC=20,∠BAC=135°
由余弦定理得BC2=AB2+AC2-2AB·AC·cos
135°=3
400,
所以BC=10
,
由正弦定理得sin∠ACB=
·sin∠BAC=
.
由∠BAC=135°知∠ACB为锐角,
故cos∠ACB=
.
故cos
θ=cos(∠ACB+45°)
=cos∠ACBcos
45°-sin∠ACBsin
45°
=
.
11.(2020·泉州二模)若ω>0,函数f(x)=3sin
ωx+4cos
ωx
的值域为
[4,5],则cos
的取值范围是( )
【解析】选D.函数f(x)=3sin
ωx+4cos
ωx=5sin(ωx+φ),
其中sin
φ=
,cos
φ=
,0<φ<
.
令t=ωx+φ,g(t)=5sin
t,
因为ω>0,0≤x≤
,所以φ≤t≤
ω+φ,
因为g(φ)=5sin
φ=4,且0<φ<
.
所以g(π-φ)=4,g(
)=5.
所以
≤
ω+φ≤π-φ,
即
-φ≤
ω≤π-2φ.
当0<
-φ≤x≤π-2φ<π时,y=cos
x单调递减.
因为cos
=sin
φ=
,
cos(π-2φ)=-cos
2φ=sin2φ-cos2φ
=
.
所以cos
的取值范围是
.
12.△ABC的内角A,B,C的对边分别为a,b,c,已知acos
=bsin
A,若b=
,
则2a+c的取值范围为( )
【解析】选C.因为A+B+C=π,
所以A+C=π-B,
因为acos
=bsin
A,
所以acos
=bsin
A,即asin
=bsin
A,
由正弦定理知,
,
所以sin
Asin
=sin
Bsin
A,因为sin
A≠0,
所以sin
=sin
B=2sin
cos
,
因为sin
≠0,所以cos
=
,
因为0<
,所以B=
.
由正弦定理知,
,
所以
,
所以a=2sin
A,c=2sin
C,
所以2a+c=4sin
A+2sin
C=4sin
A+2sin
=4sin
A+2
=3sin
A+
cos
A=2
sin
,
因为B=
,所以A∈
,
所以A+
∈
,
sin
∈
,
所以2a+c的取值范围为
.
二、填空题(共4小题,每小题5分,共20分)
13.已知0,且cos
=
,则cos
x=________.?
【解析】因为0,所以
,
又cos
=
,
所以sin
=
,
则cos
x=cos
=cos
cos
+sin
sin
=
.
答案:
14.2019年10月1日,在庆祝新中国成立70周年阅兵中,由我国自主研制的军用飞
机和军用无人机等参阅航空装备分秒不差飞越天安门,状军威,振民心,令世人瞩
目.飞行员高超的飞行技术离不开艰苦的训练和科学的数据分析.一次飞行训练
中,地面观测站观测到一架参阅直升机以72
千米/小时的速度在同一高度向正
东飞行,如图,第一次观测到该飞机在北偏西60°的方向上,1分钟后第二次观测
到该飞机在北偏东75°的方向上,仰角为30°,则直升机飞行的高度为________
千米(结果保留根号).?
【解析】如图.
由题意,得∠ABD=60°,∠CBD=75°;
AC=
=
千米;
所以∠ABC=135°;∠BAC=30°;
在△ABC中,
?
?
.
如图:
D1C⊥平面ABC,在直角△BD1C中,
tan∠D1BC=
?D1C=BC·tan∠D1BC=
×tan
30°=
千米.
答案:
15.已知锐角△ABC的内角A,B,C的对边分别为a,b,c,若a=1,2acos
C+c=2b,则角A=________,△ABC的周长的取值范围是________.?
【解析】由题意,2acos
C+c=2b,利用正弦定理,得2sin
Acos
C+sin
C=2sin
B,
(1),将sin
B=sin(A+C)=sin
Acos
C+cos
Asin
C代入(1)式得sin
C=2cos
Asin
C,
又因为sin
C≠0,故cos
A=
,所以A=
.由正弦定理可得,△ABC的周长
l△ABC=
(sin
B+sin
C)+1,将C=
-B代入化简得l△ABC=
[sin
B+sin(
-B)]+1
=2sin
+1,由0<
-B<
及0,可得
,所以
<
,
所以
≤1,所以△ABC周长的取值范围是(
+1,3].
答案:
(
+1,3]
16.(2020·新高考全国Ⅰ卷)某中学开展劳动实习,学生加工制作零件,零件的截
面如图所示,O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,
B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC=
,
BH∥DG,EF=12
cm,DE=2
cm,A到直线DE和EF的距离均为7
cm,圆孔半径为1
cm,则
图中阴影部分的面积为________cm2.?
【解析】由题意得A到DG的距离与A到FG的距离相等,均为5
cm,所以∠AOH=45°,
设O到DE的距离为5t
cm,则由tan∠ODC=
得点O到DG的距离为3t
cm,则
OAcos
45°+5t=7,OAsin
45°+3t=5,因此2t=2,t=1,OA=2
,OH=4,所以图中阴
影部分的面积为
OA2·
+
×4×2-
π=
π+4(cm2).
答案:
π+4
三角恒等变换与解三角形
关键能力·应用实践
考向一 三角恒等变换
【多维题组】速通关
1.函数y=lg
的零点是x1=tan
α和x2=tan
β,则tan
=( )
A.
B.-
C.
D.-
【解析】选C.因为函数y=lg
的零点是x1=tan
α和x2=tan
β,
所以tan
α和tan
β是方程x2+5x+4=1的两个实数根,
所以tan
α+tan
β=-5,tan
αtan
β=3,
所以
2.(2020·全国Ⅲ卷)已知sin
θ+sin
=1,则sin
=( )
A.
B.
C.
D.
【解析】选B.由题意可得:sin
θ+
sin
θ+
cos
θ=1,
则
sin
θ+
cos
θ=1,
sin
θ+
cos
θ=
,
从而有:sin
θcos
+cos
θsin
=
,
即sin
=
.
【加练备选】
(2020·全国Ⅰ卷)已知α∈(0,π),且3cos
2α-8cos
α=5,则sin
α
=( )
A.
B.
C.
D.
【解析】选A.3cos
2α-8cos
α=5,
得6cos2α-8cos
α-8=0,
即3cos2α-4cos
α-4=0,
解得cos
α=-
或cos
α=2(舍去),
又因为α∈(0,π),所以sin
α=
3.已知角α的顶点在坐标原点,始边与x轴的正半轴重合,将角α的终边按逆时针方向旋转
后经过点
,则tan
α=( )
A.-3-2
B.-3+2
C.-1
D.1
【解析】选A.设β=α+
,则tan
β=-
,
4.(2020·全国Ⅱ卷)若sin
x=-
,则cos
2x=______.?
【解析】cos
2x=1-2sin2x=1-2×
答案:
5.已知α∈
,β∈
,且
,
则cos
=( )
【解析】选C.由α∈
得
+α∈
.
又cos
所以
+α∈
,
所以
由β∈
得
又
所以
所以
=
=
【加练备选】
(2020·聊城二模)已知cos(α+
)=
,α∈
,则sin
=________.?
【解析】因为
α∈
所以
所以
则
答案:
【技法点拨】提素养
三角函数求值的类型及方法
(1)“给角求值”:利用观察得到的关系,结合三角函数公式转化为特殊角的三角函数,有时,虽不能转化为特殊角,但可通过分子分母的约分、正负项的相互抵消达到化简求值的目的.
(2)“给值求值”:关键在于“变角”,使其角相同或具有某种关系.
(3)“给值求角”:关键也是变角,把所求角用含已知角的式子表示,由所得的函数值结合该函数的单调区间求得角,有时要压缩角的取值范围.
考向二 利用正弦、余弦定理解三角形
【多维题组】速通关
1.(2020·全国Ⅲ卷)在△ABC中,cos
C=
,AC=4,BC=3,则cos
B=( )
【解析】选A.设AB=c,BC=a,CA=b,
因为c2=a2+b2-2abcos
C=9+16-2×3×4×
=9,
所以c=3,cos
B=
【加练备选】
(2020·全国Ⅲ卷)在△ABC中,cos
C=
,AC=4,BC=3,则tan
B=( )
A.
B.2
C.4
D.8
【解析】选C.设AB=c,BC=a,CA=b,因为c2=a2+b2-2abcos
C=9+16-2×3×4×
=9,
所以c=3,cos
B=
所以
所以tan
B=4
.
2.(多选题)在△ABC中,角A,B,C所对的边分别为a,b,c,下列结论正确的是( )
A.a2=b2+c2-2bccos
A
B.asin
B=bsin
A
C.a=bcos
C+ccos
B
D.acos
B+bcos
A=sin
C
【解析】选ABC.由在△ABC中,角A,B,C所对的边分别为a,b,c,知:
在A中,由余弦定理得:a2=b2+c2-2bccos
A,故A正确;
在B中,由正弦定理得:
所以asin
B=bsin
A,故B正确;
在C中,由余弦定理得:bcos
C+ccos
B=
故C正确;
在D中,由余弦定理得acos
B+bcos
A=
≠sin
C,故D
错误.故选ABC.
3.(2019·全国Ⅰ卷)△ABC的内角A,B,C的对边分别为a,b,c,已知asin
A-bsin
B
=4csin
C,cos
A=-
,则
=( )
A.6
B.5
C.4
D.3
【解析】选A.由已知及正弦定理可得a2-b2=4c2,由余弦定理推论可得-
=cos
A
=
,所以
所以
所以
×4=6.
4.(2020·南昌二模)已知梯形ABCD中,AD∥BC,AD=
,AB=4,∠ABC=60°,
∠ACB=45°,则DC=________.?
【解析】因为在△ABC中,∠ABC=60°,∠ACB=45°,
AB=4,所以由正弦定理
可得
所以
因为AD∥BC,所以∠ACB=∠DAC=45°,
所以在△ACD中,由余弦定理可得
答案:
【加练备选】
在△ABC中,已知AC=
,∠ABC=60°,AB
边上的高等于________.?
【解析】设a,b,c分别为角A,B,C的对边,因为∠ABC=60°且△ABC的面积为
,
所以
acsin
60°=
,即ac=6①
又AC=
,所以b2=a2+c2-2accos
60°=7,
即a2+c2-ac=7②
联立①②结合a>c解得:a=3,c=2.
设BC边上的高为h,所以
ah=
×3×h=
.
所以h=
.
答案:
【变式拓展】
本题条件改为“AC=3,AB=3
,∠ABC=30°,BC>AC”,求AC边上的高.
【解析】设角A,B,C的对边分别为a,b,c.
因为AC=3,AB=3
,∠ABC=30°,
所以b=3,c=3
,B=30°,
所以由余弦定理b2=a2+c2-2accos
B,
可得9=a2+27-2×a×3
×
,
整理可得a2-9a+18=0,又a>b,所以a=6.
因为S△ABC=
acsin
B=
,
所以AC边上的高的长为
5.(2020·全国Ⅰ卷)如图,在三棱锥P–ABC的平面展开图中,AC=1,AB=AD=
,
AB⊥AC,AB⊥AD,∠CAE=30°,则cos∠FCB=______.?
【解析】因为AB⊥AC,AB=
,AC=1,
由勾股定理得BC=
=2,
同理得BD=
,所以BF=BD=
,
在△ACE中,AC=1,AE=AD=
,∠CAE=30°,
由余弦定理得CE2=AC2+AE2-2AC·AEcos30°=1+3-2×1×
×
=1,
所以CF=CE=1,在△BCF中,BC=2,BF=
,CF=1,
由余弦定理得cos∠FCB=
答案:-
【技法点拨】提素养
解三角形的常见题型及求解方法
(1)已知两角A,B与一边a,由A+B+C=π及
可先求出角C及b,
再求出c.
(2)已知两边b,c及其夹角A,由a2=b2+c2-2bccos
A,先求出a,再求出角B,C.
(3)已知三边a,b,c,由余弦定理可求出角A,B,C.
(4)已知两边a,b及其中一边a的对角A,由正弦定理
可求出另一边b的
对角B,由C=π-(A+B),可求出角C,再由
可求出c,而通过
求角B时,可能有一解或两解或无解的情况.
考向三 正弦、余弦定理的实际应用
(重难突破)
【多维题组】速通关
1.如图所示,为了测量A,B两座岛屿间的距离,小船从初始位置C出发,已知A在C的
北偏西45°的方向上,B在C的北偏东15°的方向上,现在船往东开2百海里到达E
处,此时测得B在E的北偏西30°的方向上,再开回C处,由C向西开2
百海里到达
D处,测得A在D的北偏东22.5°的方向上,则A,B两座岛屿间的距离为( )
A.3百海里
B.3
百海里
C.4百海里
D.4
百海里
【考场思维】
解题方法
直接计算
解题流程
利用方向角求出三角形中各个角的大小→利用正弦定理求出AC和BC→利用余弦定理求出结果.
素养考查
数学运算、直观想象
【解析】选B.根据题意知:∠ADC=∠DAC=67.5°,
∠ACB=60°,DC=2
,CE=2,∠BCE=75°,∠CBE=45°,∠CEB=60°.
所以在△BCE中,利用正弦定理
解得BC=
,
在△ADC中,∠ADC=∠DAC=67.5°,
所以DC=AC=2
,
则在△ACB中,利用余弦定理AB2=AC2+CB2-2AC·CB·cos
60°,解得AB=3
,
所以A,B两座岛屿的距离为3
百海里.
2.某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射
高度:在C处(点C在水平地面下方,O为CH与水平地面ABO的交点)进行该仪器的垂
直弹射,水平地面上两个观察点A,B两地相距100米,∠BAC=60°,其中A到C的距离
比B到C的距离远40米.A地测得该仪器在C处的俯角为∠OAC=15°,A地测得最高点
H的仰角为∠HAO=30°,则该仪器的垂直弹射高度CH为( )
A.210(
+
)米
B.140
米
C.210
米
D.20(
-
)米
【考场思维】
解题方法
建立方程求解
解题流程
设AC=x米,则BC=(x-40)米→在△ABC内,由余弦定理构建方程求出AC→在△ACH中,用正弦定理求CH.
素养考查
数学运算、直观想象
【解析】选B.由题意,设AC=x米,则BC=(x-40)米,在△ABC内,由余弦定理得
BC2=BA2+CA2-2BA·CA·cos∠BAC,
即(x-40)2=x2+10
000-100x,解得x=420.
在△ACH中,AC=420米,
∠CAH=30°+15°=45°,∠CHA=90°-30°=60°,
由正弦定理
可得CH=AC·
=140
(米).
【技法点拨】提素养
解三角形实际应用问题的步骤
【变式训练】
1.为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积为( )
A.
km2
B.
km2
C.
km2
D.
km2
【解析】选D.如图,连接AC,根据余弦定理可得AC=
,故△ABC为直角三角形,
且∠ACB=90°,∠BAC=30°,从而△ADC为等腰三角形,且∠ADC=150°,设AD=DC=x,
根据余弦定理得x2+x2+
x2=3,即x2=
所以所求小区的面积为
×1×
+
×3(2-
)×
=
(km2).
2.《海岛算经》是中国学者刘徽编撰的一部测量数学著作,现有取自其中的一个
问题:今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表参相直,从前
表却行一百二十三步,人目着地,取望岛峰,与表末参合,从后表却行一百二十七
步,人目着地,取望岛峰,亦与表末参合,问岛高几何?其大意为:如图所示,立两个
三丈高的标杆BC和DE,两标杆之间的距离BD=1
000步,两标杆的底端与海岛的底
端H在同一直线上,从前面的标杆B处后退123步,人眼贴地面,从地上F处仰望岛
峰,A,C,F三点共线,从后面的标杆D处后退127步,人眼贴地面,从地上G处仰望岛
峰,A,E,G三点也共线,则海岛的高为(注:1步=6尺,1里=180丈=1
800尺=300步)
( )
A.1
255步
B.1
250步
C.1
230步
D.1
200步
【解析】选A.因为AH∥BC,所以△BCF∽△HAF,所以
因为AH∥DE,
所以△DEG∽△HAG,所以
又BC=DE,所以
即
所以HB=30
750步,
又
所以AH=
=1
255(步).
3.如图所示,在山脚A测得山顶P的仰角为∠QAP=45°,沿倾斜角为∠QAB=15°的
斜坡向上走146.4米到达B,在B测得山顶P的仰角为∠CBP=60°,则山高PQ约为
________米.?(
≈1.414,
≈1.732,结果保留到小数点后1位)
【解析】∠PAB=∠PAQ-∠BAQ=45°-15°=30°,
∠APB=∠QPA-∠CPB=45°-(90°-60°)=15°.
∠ABP=180°-(∠PAB+∠APB)=135°,
在△PAB中,由正弦定理得
即
PQ=APsin∠PAQ=
≈282.8(米).
答案:282.8
【加练备选】
已知在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.轮船沿BC行驶一段时间后,到达海岛的正西方向的D处,此时轮船距岛A有________千米.?
【解析】由已知可求得AB=
,AC=
,BC=
,
所以sin∠ACB=
,cos∠ACB=
,则∠ACB为锐角,∠ACD为钝角,
且sin∠ACD=
,cos∠ACD=-
.
在△ACD中,sin∠ADC=sin(∠ACD+∠DAC)
=sin∠ACDcos∠DAC+sin∠DACcos∠ACD
由正弦定理可求得AD=
答案:
题组训练·素养提升
【新题速递】
1.已知角α的顶点在坐标原点O,始边与x轴的非负半轴重合,将角α的终边绕O点
顺时针旋转
后,经过点(-3,4),则sin
α=( )
A.
B.
C.
D.-
【解析】选B.角α的终边按顺时针方向旋转
后得到的角为α-
,
所以由三角函数的定义,可得:
所以sin
α=sin
2.(2020·青岛模拟)若函数f(x)=sin
2xsin
φ+2cos2xcos
φ-cos
φ
的一个极大值点为
,则φ=( )
A.0
B.
C.
D.
【解析】选D.f(x)=sin
2xsin
φ+2cos2xcos
φ-cos
φ=sin
2xsin
φ+
(2cos2x-1)cos
φ=sin
2xsin
φ+cos
2xcos
φ=cos
,因为f(x)的一
个极大值点为
,所以f
=cos
=1,解得φ=
+2kπ,k∈Z,又0<φ<π,
故φ=
.
3.2020年5月27日,中国珠穆朗玛峰测高工程队顺利登顶,将在峰顶竖立站标,安装GNSS(全球卫星导航系统),将对这座世界最高峰的高度进行最新测量,如在水平面上的A处测得峰顶H的仰角是45°,然后在另一点B处测得峰顶H的仰角是60°,若H在水平面的射影为O(如图),且∠AOB=150°,AB=a,则珠穆朗玛峰的最新高度OH=________.?
【解析】设OH=h,由题可知:∠OAH=45°,∠OBH=60°,
则AO=h,BO=
h,
在△AOB中,有AB2=AO2+BO2-2AO·BO·cos∠AOB,
又AB=a,所以a2=h2+
-2h·
·cos
150°,
则h2=
?h=
a.
答案:
a
4.(2020·大庆三模)已知函数f(x)=2sin2x+
asin
2x的最大值为3,则实数a的
值为________.?
【解析】由题得f(x)=2sin2x+
asin
2x=1-cos
2x+
asin
2x
=
sin(2x+φ)+1,其中tan
φ=-
,
所以f(x)的最大值为
+1=3,解得a=±1.
答案:±1
5.在△ABC中,角A,B,C所对的边分别为a,b,c.已知a=2
,b=5,c=
.则
C=________;sin
=________.?
【解析】在△ABC中,由a=2
,b=5,c=
及余弦定理得
又因为C∈(0,π),所以C=
.
在△ABC中,由C=
,a=2
,c=
及正弦定理,
可得
由a
,
可得
进而sin
2A=2sin
Acos
A=
cos
2A=2cos2A-1=
,
所以sin
=sin
2Acos
+cos
2Asin
=
答案:
【创新迁移】
1.有一道题目由于纸张破损,有一条件看不清楚,具体如下:“在△ABC中,角
A,B,C的对边分别为a,b,c,已知a=
,________,c2-b2-3c+3=0,求角A.”经推断,
破损处的条件为三角形一边的长度,且该题的答案A=
是唯一确定的,则破损处
应是________.?
【解析】因为c2-b2-3c+3=0,a=
.
所以c2-b2-
ac+a2=0,
即
所以cos
B=
,又B∈(0,π),所以B=
.
(1)由正弦定理可知,
可得b=
.
检验:
又因为A∈(0,π)且a>b,
所以A=
或者A=
,这与已知角A的解为唯一解矛盾.
(2)B=
,A=
,所以C=
,
由正弦定理可知,
检验:
又A∈(0,π),且c>a,
所以A=
.故应填的条件是:c=
答案:c=
2.顶角为36°的等腰三角形称为“黄金三角形”,黄金三角形看起来标准又美观.
如图所示,△ABC是黄金三角形,AB=AC,作∠ABC的平分线交AC于点D,易知△BCD也
是黄金三角形.若BC=1,则AB=______;借助黄金三角形可计算sin
234°=______.?
【解析】由题可得∠A=∠ABD=∠DBC=36°,∠C=∠BDC=72°,所以△ABC∽△BCD,
得
,且AD=BD=BC=1.
设AB=AC=x,则CD=x-1,所以
,
可解得x=
(负值舍去),所以AB=
因为sin
234°=sin(180°+54°)=-sin
54°=-cos
36°.
在△ABC中,根据余弦定理可得cos
36°=
所以sin
234°=-
.
答案:
-
专题能力提升练
五 三角恒等变换与解三角形
(40分钟 80分)
一、选择题(共12小题,每小题5分,共60分)
1.若cos
78°=m,则sin(-51°)=( )
【解析】选A.因为cos
78°=m,
所以cos(180°-78°)=cos
102°
=-cos
78°=-m,
可得1-2sin251°=cos
102°=-m,
所以sin251°=
,解得:sin
51°=
,
所以sin(-51°)=
.
2.在△ABC中,角A,B,C所对的边分别为a,b,c,若b=2
,c=3,B=2C,则cos
2C的值为( )
【解析】选B.由正弦定理可得,
,
所以
又b=2
,c=3,所以2cos
C=
,cos
C=
,
所以cos
2C=2cos2C-1=2×
-1=
.
3.
=( )
A.1
B.2
C.
D.
【解析】选C.原式=
4.已知α为锐角,β为第二象限角,且cos(α-β)=
,sin(α+β)=
,则sin(3α-β)=( )
【解析】选B.因为α为锐角,β为第二象限角,cos(α-β)>0,sin(α+β)>0,
所以α-β为第四象限角,α+β为第二象限角,
因此sin(α-β)=-
,cos(α+β)=-
,所以sin
2α=sin(α-β+α+β)
=sin
(α-β)cos
(α+β)+cos
(α-β)sin
(α+β)
=
=1.
因为α为锐角,所以2α=
,
所以sin(3α-β)=sin(2α+α-β)=cos(α-β)=
.
【一题多解】解答本题还可以有如下解法:
由上面可得,sin(α-β)=-
,cos(α+β)=-
.
所以cos2(α-β)=2cos2(α-β)-1
=2×
,
sin2(α-β)=2sin(α-β)cos(α-β)
=2×
.
所以sin(3α-β)=sin[2(α-β)+(α+β)]
=sin
2(α-β)·cos(α+β)+cos
2(α-β)·sin(α+β)
=
.
5.函数f(x)=2sin2ωx+sin
2ωx-1的图象向左平移
个单位长度后,与原图象有
相同的对称轴,则正实数ω的最小值是( )
A.1
B.2
C.4
D.6
【解析】选B.因为f(x)=2sin2ωx+sin
2ωx-1=sin
2ωx-cos
2ωx
=
sin
,
将其图象向左平移
个单位长度后,
可得y=
sin
=
sin
的图象.
由于所得的图象与原图象有相同的对称轴,
所以
=kπ,k∈Z,即ω=2k,k∈Z,
则正实数ω的最小值为2.
6.在△ABC中,cos2
=
(a,b,c分别为角A,B,C的对边),则△ABC的形状为
( )
A.正三角形
B.直角三角形
C.等腰三角形或直角三角形
D.等腰直角三角形
【解析】选B.因为cos2
=
,
所以
,
所以
,化简得a2+b2=c2.
故△ABC是直角三角形.
7.(多选题)下列选项中,值为
的是( )
A.cos
72°cos
36°
B.
C.
D.
【解析】选AB.对于A,cos
36°cos
72°
故A正确;
对于B,
故B正确;
对于C,原式=
故C错误;
对于D,
-
cos215°=-
(2cos215°-1)
=-
cos
30°=-
,故D错误.
8.(2020·中卫二模)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知
C=
,sin
B=3sin
A,若△ABC的面积为6
,则c=( )
【解题导引】由sin
B=3sin
A可得b=3a,再利用面积公式得到a,b的方程组,解出
a,b,最后利用余弦定理求出c的值.
【解析】选B.因为sin
B=3sin
A,所以b=3a,
又因为C=
,△ABC的面积为6
,
所以S=
absin
C=
a2×sin
=6
,
解得a=2
,b=6
,
所以c2=a2+b2-2abcos
C=
=104.
所以c=2
.
【加练备选】
在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若sin
A=
,a=2,S△ABC=
,
则b的值为( )
【解析】选A.由S△ABC=
bcsin
A=
bc×
=
,解得bc=3.
因为A为锐角,sin
A=
,所以cos
A=
,
由余弦定理得a2=b2+c2-2bccos
A,代入数据解得b2+c2=6,则(b+c)2=12,b+c=2
,
所以b=c=
.
9.(2020·郑州三模)在△ABC中,角A,B,C所对的边分别为a,b,c.
若
asin
B=c-bcos
A,则角B等于( )
【解析】选A.因为
asin
B=c-bcos
A,
所以由正弦定理可得
sin
Asin
B=sin
C-sin
Bcos
A,
所以
sin
Asin
B+sin
Bcos
A=sin
C,
因为sin
C=sin(A+B)
=sin
Acos
B+cos
Asin
B,
所以
sin
Asin
B=sin
Acos
B,因为sin
A≠0,
所以
sin
B=cos
B,可得tan
B=
,
因为B∈(0,π),所以B=
.
10.如图所示,位于A处的信息中心获悉:在其正东方向相距30
海里的B处有一
艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西45°、相距
20海里的C处的乙船,现乙船朝北偏东θ的方向沿直线CB前往B处救援,则cos
θ
的值为( )
【解析】选B.在△ABC中,AB=30
,
AC=20,∠BAC=135°
由余弦定理得BC2=AB2+AC2-2AB·AC·cos
135°=3
400,
所以BC=10
,
由正弦定理得sin∠ACB=
·sin∠BAC=
.
由∠BAC=135°知∠ACB为锐角,
故cos∠ACB=
.
故cos
θ=cos(∠ACB+45°)
=cos∠ACBcos
45°-sin∠ACBsin
45°
=
.
11.(2020·泉州二模)若ω>0,函数f(x)=3sin
ωx+4cos
ωx
的值域为
[4,5],则cos
的取值范围是( )
【解析】选D.函数f(x)=3sin
ωx+4cos
ωx=5sin(ωx+φ),
其中sin
φ=
,cos
φ=
,0<φ<
.
令t=ωx+φ,g(t)=5sin
t,
因为ω>0,0≤x≤
,所以φ≤t≤
ω+φ,
因为g(φ)=5sin
φ=4,且0<φ<
.
所以g(π-φ)=4,g(
)=5.
所以
≤
ω+φ≤π-φ,
即
-φ≤
ω≤π-2φ.
当0<
-φ≤x≤π-2φ<π时,y=cos
x单调递减.
因为cos
=sin
φ=
,
cos(π-2φ)=-cos
2φ=sin2φ-cos2φ
=
.
所以cos
的取值范围是
.
12.△ABC的内角A,B,C的对边分别为a,b,c,已知acos
=bsin
A,若b=
,
则2a+c的取值范围为( )
【解析】选C.因为A+B+C=π,
所以A+C=π-B,
因为acos
=bsin
A,
所以acos
=bsin
A,即asin
=bsin
A,
由正弦定理知,
,
所以sin
Asin
=sin
Bsin
A,因为sin
A≠0,
所以sin
=sin
B=2sin
cos
,
因为sin
≠0,所以cos
=
,
因为0
,所以B=
.
由正弦定理知,
,
所以
,
所以a=2sin
A,c=2sin
C,
所以2a+c=4sin
A+2sin
C=4sin
A+2sin
=4sin
A+2
=3sin
A+
cos
A=2
sin
,
因为B=
,所以A∈
,
所以A+
∈
,
sin
∈
,
所以2a+c的取值范围为
.
二、填空题(共4小题,每小题5分,共20分)
13.已知0
=
,则cos
x=________.?
【解析】因为0
,
又cos
=
,
所以sin
=
,
则cos
x=cos
=cos
cos
+sin
sin
=
.
答案:
14.2019年10月1日,在庆祝新中国成立70周年阅兵中,由我国自主研制的军用飞
机和军用无人机等参阅航空装备分秒不差飞越天安门,状军威,振民心,令世人瞩
目.飞行员高超的飞行技术离不开艰苦的训练和科学的数据分析.一次飞行训练
中,地面观测站观测到一架参阅直升机以72
千米/小时的速度在同一高度向正
东飞行,如图,第一次观测到该飞机在北偏西60°的方向上,1分钟后第二次观测
到该飞机在北偏东75°的方向上,仰角为30°,则直升机飞行的高度为________
千米(结果保留根号).?
【解析】如图.
由题意,得∠ABD=60°,∠CBD=75°;
AC=
=
千米;
所以∠ABC=135°;∠BAC=30°;
在△ABC中,
?
?
.
如图:
D1C⊥平面ABC,在直角△BD1C中,
tan∠D1BC=
?D1C=BC·tan∠D1BC=
×tan
30°=
千米.
答案:
15.已知锐角△ABC的内角A,B,C的对边分别为a,b,c,若a=1,2acos
C+c=2b,则角A=________,△ABC的周长的取值范围是________.?
【解析】由题意,2acos
C+c=2b,利用正弦定理,得2sin
Acos
C+sin
C=2sin
B,
(1),将sin
B=sin(A+C)=sin
Acos
C+cos
Asin
C代入(1)式得sin
C=2cos
Asin
C,
又因为sin
C≠0,故cos
A=
,所以A=
.由正弦定理可得,△ABC的周长
l△ABC=
(sin
B+sin
C)+1,将C=
-B代入化简得l△ABC=
[sin
B+sin(
-B)]+1
=2sin
+1,由0<
-B<
及0
,
所以
+1,3].
答案:
(
+1,3]
16.(2020·新高考全国Ⅰ卷)某中学开展劳动实习,学生加工制作零件,零件的截
面如图所示,O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,
B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC=
,
BH∥DG,EF=12
cm,DE=2
cm,A到直线DE和EF的距离均为7
cm,圆孔半径为1
cm,则
图中阴影部分的面积为________cm2.?
【解析】由题意得A到DG的距离与A到FG的距离相等,均为5
cm,所以∠AOH=45°,
设O到DE的距离为5t
cm,则由tan∠ODC=
得点O到DG的距离为3t
cm,则
OAcos
45°+5t=7,OAsin
45°+3t=5,因此2t=2,t=1,OA=2
,OH=4,所以图中阴
影部分的面积为
OA2·
+
×4×2-
π=
π+4(cm2).
答案:
π+4
同课章节目录
